灰色变异粒子群算法在公交客流量预测中的应用＊

米根锁，梁 利，杨润霞

（兰州交通大学自动化与电气工程学院，甘肃 兰州730070）

1 引言

公交客流量是公交系统规划和发展的基础数据，由于公交客流量影响因素的随机性、不确定性和复杂性，因此一些传统的预测法预测的客流量与实际客流量之间存在较大的偏差［1～3］。灰色理论适合于不确定、随机因素影响领域的预测，并在这些预测领域中得到了广泛的应用［4］。公交客流量的预测可看作是个灰色系统，将灰色理论引入到公交客流量预测领域中，运用灰色预测法来预测未来的公交客流量［5］。但是，传统灰色预测法在求解模型参数时采用最小二乘法，最终建立的模型求得的预测值与实际值拟合度较差，预测结果误差较大，预测的精度不高［6］。针对以上问题，本文在传统灰色预测法的基础上，引入变异粒子群算法对灰色预测模型中的参数进行优化，以提高其预测精度，使其能对公交客流量进行准确预测。并选取1987年～1991年及1994年～2003年铜州市公交客流量的实际数据，对灰色变异粒子群组合预测模型的精度和可行性进行分析，仿真结果得出该组合预测模型优于传统的（单变量一阶灰色预测模型）GM（1，1）及其他几种常用预测算法。用此组合预测模型来预测公交客流量，能准确地预测出未来公交客流量的大小，为公交系统的规划与建设提供准确的数据，有利于城市公交的快速发展。

2 传统的灰色GM（1，1）模型

灰色系统采用将原始数据进行直接累加或者移动平均加权累加的方法，生成具有一定规律的新数列，且利用特定的曲线逼近其相应曲线，以逼近的曲线作为模型，对待预测系统进行预测。该方法的优点是预测时需要的原始数据较少，数据分布可以随机，仅需原始时间数据序列即可［7］。

目前，在灰色系统理论中应用最为普遍的一种预测模型是GM（1，1），其不受一般统计模型对原始数据各种要求的约束限制，且考虑影响因素较少，具有较强的有效性和实用性。在建立GM（1，1）模型时，首先要对原始数据数列进行处理，构造出规律性较强的新数列，即对原始数列进行一次累加，生成新的数列。其建模过程如下：

原始数据数列X（0）：

对式（1）进行一次累加生成新数列X（1）：

由于累加生成的式（2）新数列能将任意非负数列转化为非减的递增数列，因此使该数列减弱了随机性，加强了规律性。

对式（2）中的X（1）建立其白化方程为：

式（3）是含一个变量的一阶微分方程，记为GM（1，1）。记参数数列运用最小二乘法求解参数：

式（4）中矩阵B为：

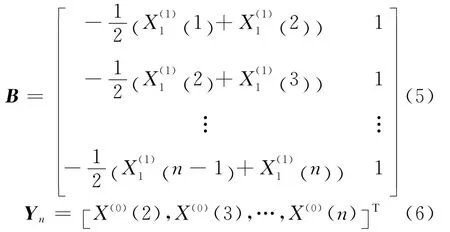
求得微分方程（3）的响应方程为：

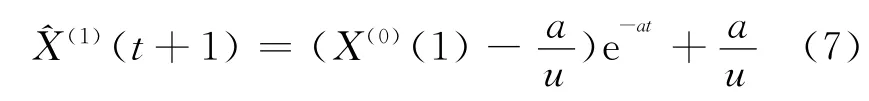
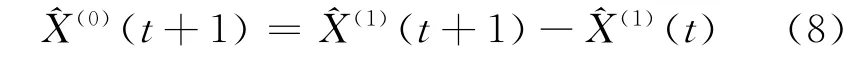
3 变异粒子群算法

1995年Kennedy 和Ebehart提出了粒子群PSO（Particle Swarm Optimization）算法，PSO 算法最初的思想源于对鸟群的群体捕食行为的研究。在群体中，各个个体通过信息共享和交流搜索出食物所在的位置，即待优化问题的最优解。在该算法中，每个个体就是待优化问题的一个随机解，即被称之为“粒子”。每个粒子具有各自一个适应值，该适应值由待优化问题的目标函数决定，每个粒子还具有各自的飞行速度和方向。PSO 算法开始先随机初始化一群粒子（随机解）及其速度，然后每个粒子根据一定的公式更新自己的位置和速度，迭代直到满足终止条件为止。每一次迭代过程中，每个粒子依据个体极值Pi和全局极值Pg来更新自身的飞行方向（位置）和速度，最终找到全局位置最优的那个粒子（最优解），即优化问题的最优解。每个粒子更新自己的速度和位置的公式如下：

其中，Vi（t）是粒子i在第t次迭代的速度；Xi（t）是粒子i第t次迭代的位置；rand（）是随机数，取值为（0，1）之间的数；C1、C2是学习因子，一般在（0，2）间取值；W是惯性因子。粒子群算法虽然有很好的鲁棒性，但容易陷入局部最优。为了克服该算法的缺点，文献［8］对该算法进行改进，避免陷入局部最优，使得在优化中达到全局最优。本文基于此文献改进PSO 算法，加入变异算子的思想，在粒子群算法中加入变异因子，即在粒子陷入局部最优时，按照一定的扰动方式对部分最优解重新初始化，避免了陷入局部最优，在全局中搜索出最优解。首先判断粒子的群体适应度方差σ2，当σ2等于或低于设定阈值时，粒子群有可能陷入局部最优，粒子找到的解有可能是局部最优解［8］，同时根据式（10）判定需初始化的粒子数目是否大于或等于2/n，对个体极值远离全局极值的粒子重新初始化，跳出在局部范围搜索，其初始化判断公式如下：

其中，gbest为当前粒子群群体最优解；gi为个体粒子i最优解；gmin为非扰动下限值；gmax为非扰动上限值。若gmin≤p≤gmax则粒子群不初始化，否则初始化。为了表述本文加入变异算子的性能优于文献［8］，以三个简单的函数为测试对象，对本文加入变异因子使粒子群算法跳出局部最优的变异算法与带变异算子的自适应粒子群优化算法（PSOH）的收敛性能进行比较。

求解f1（x）＝x2＋2的最小值，在测试中学习因子采用非对称形式（提高收敛速度），C1＝0.4，C2＝0.9；惯性权重为Wmin＝0.2，Wmax＝0.8；种群数n＝50；最大迭代次数nmax＝30。两种算法的性能仿真结果如图1所示。

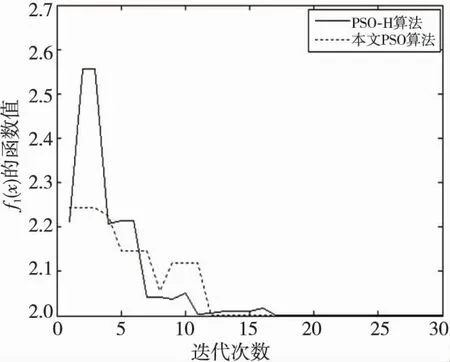
Figure 1 Function f1（x）optimization evolutionary curves图1 函数f1（x）寻优进化曲线

测试结果表明，PSO－H 算法在第17次达到最优值2，而本文加入变异因子后，在第12次达到最优解，该算法的性能明显优于PSO－H 算法，避免了PSO 陷入局部收敛，具有良好的性能，同时也说明了加入变异算子改进粒子群算法的可行性和优越性。

求解f2（x）＝10cos（2πx）＋10的最小值，测试中C1＝0.4，C2＝0.9；惯性权重为Wmin＝0.2，Wmax＝0.8；种群数n＝30；最大迭代次数nmax＝50。两种算法的性能仿真结果如图2所示。

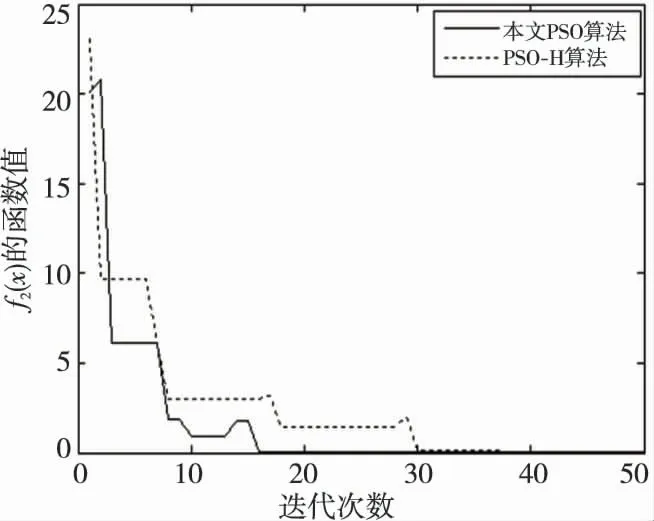
Figure 2 Function f2（x）optimization evolutionary curves图2 函数f2（x）寻优进化曲线图

测试结果表明，PSO－H 算法在第31次达到最优值0，而本文加入变异因子后，在第16次达到最优解。

求解f3（x）＝5sin（2πx）＋2的最小值，测试中C1＝0.4，C2＝0.9；惯性权重为Wmin＝0.2，Wmax＝0.8；种群数n＝30；最大迭代次数nmax＝50。两种算法的性能仿真结果如图3所示。

Figure 3 Function f3（x）optimization evolutionary curves图3 函数f3（x）寻优进化曲线图

通过图1～图3可知，该算法的性能明显优于PSO－H 算法，避免了PSO 陷入局部收敛，具有良好的性能，同时也说明了加入变异算子改进粒子群算法的可行性和优越性。

4 灰色变异粒子群组合模型的建立

4.1 灰色GM（1，1）模型局限性分析

文献［6］研究表明，GM（1，1）模型运用最小二乘法求解参数时，由于式（3）将作为已知条件，因此，所求解的参数存在较大的系统误差，无法满足拟合条件，求得的预测方程不一定是最优的预测方程，结果会影响预测的精度，所建立的预测模型的精度方差比C及小误差概率P较差，精度评价表如表1所示［9］。由于粒子群算法可以用于参数优化研究中［10］，因此，本文运用变异粒子群算法优化此模型的参数a、u，在可行解范围内寻求最优参数解，以最优参数来建立预测模型，提高灰色GM（1，1）的预测精度，能准确地预测未来公交客流量。

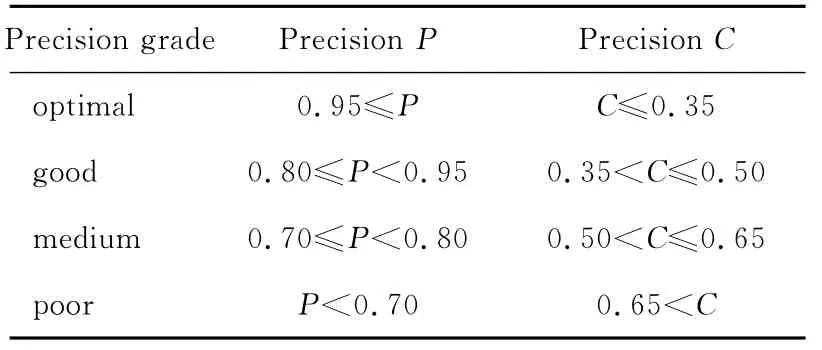
Table 1 Model precision表1 模型精度表

4.2 灰色变异粒子群组合模型建立

由表1 可知，方差比C越小，预测的精度越高，本文以方差比为目标函数，在a、u的可行解范围内寻求满足目标函数最小的最优参数a、u的值，建立精度较高的预测模型。

方差比：

其中，S1为原始数据的均方差，S2为残差的均方差。

建立组合预测模型的步骤如下：

（1）读取原始数据序列。

（2）t＝1时，初始化粒子群。随机初始化粒子的位置x和速度v；设定粒子的数目n；设定其它参数值。每个粒子都是一个二维向量，分别代表参数a和u。

（3）设定非扰动下限值gmin及非扰动上限值gmax；设定适应度方差阈值。

（4）随机初始化全局最优解gbest及其局部最优gi。

（5）根据式（9）每个粒子更新自己的速度和位置，并不断更新全局最优粒子。

（6）求解适应度函数值。每个粒子依据式（11）计算自身的适应值。适应值是评价粒子位置优劣的依据。

（7）每个粒子更新自己搜索的个体最优值和群体最优值。

（8）计算适应度方差值σ2。如果σ2等于零或者低于阈值，则算法可能陷入局部最优，且根据式（10）判断远离全局极值的粒子数目是否大于或等于2/n，若是则转至步骤（10），否则转至步骤（9）。

（9）判断是不是达到最大迭代次数，若是，则输出最优参数a、u，否则跳至步骤（5）。

（10）根据式（10），对部分粒子进行扰动变异即重新初始化，转至步骤（6）。

（11）根据步骤（9）求解的最优参数a和u，建立预测模型，计算出预测数据。

5 实例分析

原始数据数列的选取为1994 年～2003 年铜州市公交客流量的历史客流量数据（1991年、1992年、1993年 历 史 客 流 分 别 为2 194 万 次、2 130 万次、1 918万次）。在MATLAB R2007b环境下实现了传统单一GM（1，1）灰色预测模型和灰色变异粒子群组合预测模型预测公交客流量的仿真。在实验中学习因子C1＝0.4，C2＝0.9；惯性权重为Wmin＝0.2，Wmax＝0.8；种群数n＝50；最大迭代次数nmax＝50。两种算法的性能仿真结果如表2所示。

Table 2 Simulation results表2 仿真结果表

从仿真结果可以看出，组合模型的预测相对误差低于GM（1，1）预测数据的相对误差，该组合模型预测出的客流量更接近实际客流量值，误差相对较小。因此，将灰色预测法与变异粒子群算法相结合，建立一种组合预测模型能很好地预测公交客流量，预测误差明显低于单一GM（1，1）预测模型的预测误差。两种预测模型的C、P精度比较及平均误差如表3所示。

由表3可知，以方差比为目标函数，运用变异粒子群算法搜索最优的参数a、u，建立的预测模型平均误差小于单一传统的GM（1，1）预测模型的平均误差。两种模型求解预测值与实际值的拟合趋势如图4所示。

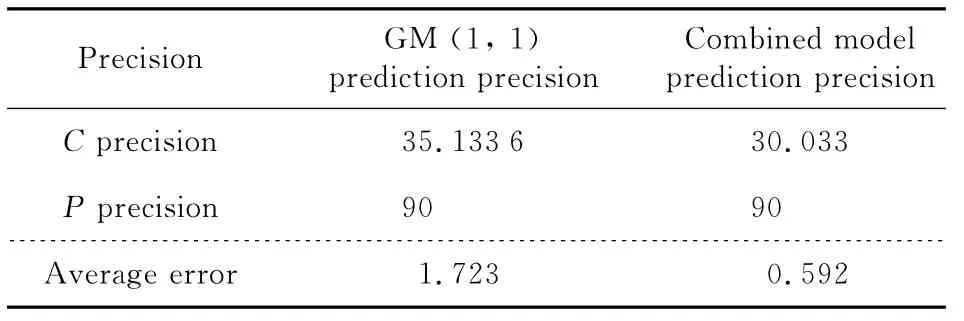
Table 3 Comparison of Precision表3 精度比较表 %

Figure 4 Fitting between the predicted values and actual values of the two models图4 两种模型预测值与实际值的拟合趋势

由图4可知，组合预测模型预测的客流量与实际的客流量拟合较好，更接近实际数据。而单一GM（1，1）预测模型所预测的客流量与实际客流量拟合较差，偏差较大。相比灰色变异粒子群组合模型预测精度较高，更具有实用性。

为了进一步说明组合预测模型的优越性，选取1987年～1991年铜州市公交客流量为原始数据进行与随机灰色预测［11］、递归网络模型预测［12］、随机灰色蚁群神经网络组合模型预测［13］仿真对比，验证此组合预测模型预测的优越性。预测值如表4所示，对比仿真图如图5所示，相对误差对比如表5所示。

Figure 5 Simulation of predicted data图5 预测值对比仿真图

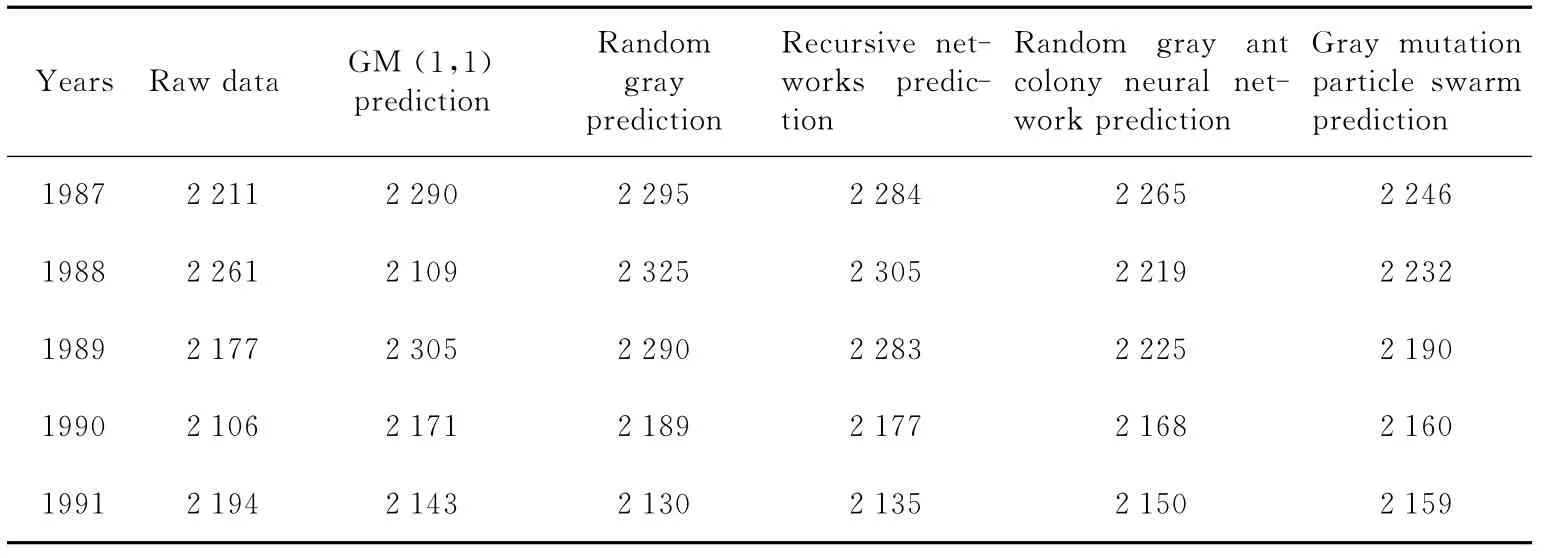
Table 4 Prediction values（/Ten thousands times）表4 预测值表 万次

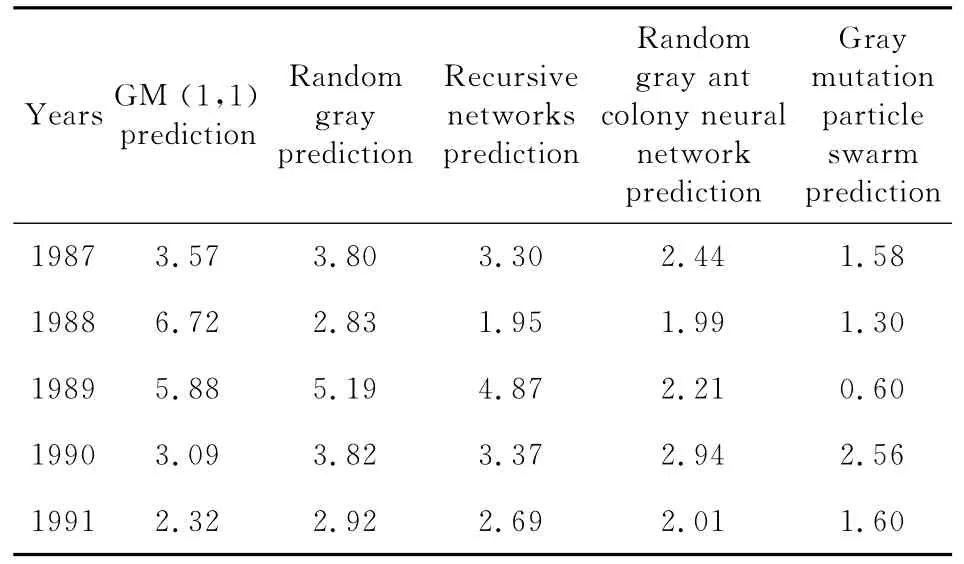
Table 5 Comparison of relative error表5 相对误差对比表 %

几种模型的相对平均误差对比如表6所示。

Table 6 Comparison of average error表6 平均误差对比表 %

几种模型的相对误差比较如图6所示。

Figure 6 Relative error figure图6 相对误差图

本文以1991年的客流量为例，通过以上几种算法对其预测，并对本文算法的收敛性能进行分析，仿真图如图7所示。

从图6可知，GM（1，1）算法第33次达到最优值2 143万次，随机灰色算法第28 次达到最优值2 130万次，递归网络算法第25次达到最优值2 135万次，随机灰色蚁群神经网络算法第21次达到最优值2 150万次，本文PSO 算法第15次达到最优值2 159万次，由此可知，本文改进算法优于其他几种常用预测算法，收敛性能较好。

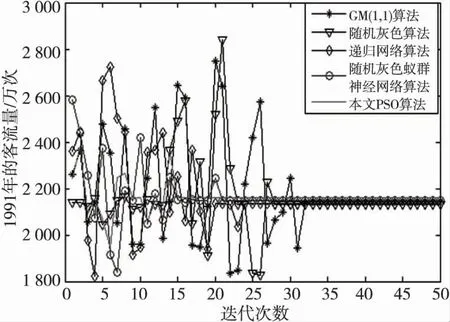
Figure 7 Algorithm optimization evolutionary curves图7 算法寻优进化曲线图

由图6可知，组合预测模型的相对误差小于其他几种预测算法的相对误差，从图7可看出，本文改进PSO 算法的收敛性能明显优于其他几种预测算法。实例表明，变异粒子群组合预测模型的预测精度明显高于单一GM（1，1）预测模型及其其他几种预测算法的预测精度，预测值更接近实际值，运用此组合预测模型更能准确地预测未来客流量的大小。

6 结束语

本文结合灰色理论与变异粒子群算法建立了一种灰色变异粒子群组合预测模型，通过具体的函数验证了算法的优越性，并通过实例验证分析表明，组合预测模型的预测精度明显高于单一GM（1，1）预测模型及其其他几种常用预测算法。因此，运用变异粒子群算法优化传统灰色预测模型的参数，明显提高了预测精度，将此组合模型运用到公交客流量预测中，预测数据与实际数据拟合较好，能准确地预测出公交客流量，为公交系统的发展与规划提供科学的基础依据，从而能够合理地建设公交系统，促进公交系统的快速发展。

［1］ Zhang Chun－hui，Song Rui，Sun Yang.The short－term passenger flow prediction of bus stations based on kalman filtering［J］.Journal of Transportation Systems Engineering and InformationTechnology，2011，11（4）：154－159.（in Chinese）

［2］ Yan Qi－sheng，Wang Shi－tong.Support vector regression model of highway traveling passenger volume traffic forecasting［J］.Computer Engineering and Applications，2011，47（9）：233－235.（in Chinese）

［3］ Hong Bing－rong，Jin Fei－hu，Gao Qing－ji.Multi－layer feedforward neural network based on ant colony system ［J］.Journal of Harbin Institute of Technology，2003，35（7）：823－825.（in Chinese）

［4］ Zhang Cheng，Zhou Xiang－feng.Prediction of railway freight volumes based on grey forcast－markov chain－qualitative analysis［J］.Journal of Railway，2007，29（5）：15－21.（in Chinese）

［5］ Fang Li－jun，Wu Zhong.The application of GM（1，3）model in highway passenger capacity forcast of transportion system［J］.Journal of Highway and Transportion Research and Development，2006，23（3）：163－166.（in Chinese）

［6］ Zhang Da－hai，Wang Shi－fang，Shi kai－quan.Theoretical defect of grey prediction formula and its improvement［J］.Systems Engineering－Theory＆ Practice，2002，22（8）：1－3.（in Chinese）

［7］ Rui Liu，Li Xiao－lei，Liu Si－feng.Deformation monitoring and forcasting model study based on grey system theory［J］.Advances in Intelligent and Soft Computing，2009，62：555－564.

［8］ Zhao Zhi－gang，Chang Cheng.Adaptive particle swarm optimization algorithm with hybrid mutation operator［J］.Computer Engineering and Application，2011，47（17）：42－44.（in Chinese）

［9］ Deng Ju－long.Grey theory［M］.Wuhan：Huazhong University of Science and Technology Press，2002.（in Chinese）

［10］ Li Song，Liu Li－jun，Liu Ying－peng.Prediction for chaotic time series of optimized BP neural network Based on modified PSO［J］.Computer Engineering and Applications，2013，49（6）：245－246.（in Chinese）

［11］ Zhang Fei－lian，Shi Feng.Stochastic gray system model for forcasting passenger and freight railway volume［J］.Journal of Central South University，2005，36（1）：158－159.（in Chinese）

［12］ Zhang Yan，Wang Fan－zhen，Chen zeng－qiang，et al.Recurrent neural networks－based multivariable system predictive control［J］.Journal of Nankai University，2006，39（1）：49－53.（in Chinese）

［13］ Wang Qing－rong，Zhang Qiu－yu.Forecasting of short－terms urban public transit volume based on random gray ant colony neural network［J］.Application Research of Computers，2012，29（6）：2080－2084.（in Chinese）

中文参考文献：

［1］ 张春辉，宋瑞，孙杨.基于卡尔曼滤波的公交站点短时客流预测［J］.交通运输系统工程与信息，2011，11（4）：154－159.

［2］ 颜七笙，王士同.公路旅游客流量预测的支持向量回归模型［J］.计算机工程与应用，2011，47（9）：233－235.

［3］ 洪炳熔，金飞虎，高庆吉.基于蚁群算法的多层前馈神经网络［J］.哈尔滨工业大学学报，2003，35（7）：823－825.

［4］ 张诚，周湘峰.基于灰色预测－马尔可夫链－定性分析的铁路货运量预测［J］.铁道学报，2007，29（5）：15－21.

［5］ 方丽君，吴中.GM（1，3）模型在交通系统公路客运量预测中的应用［J］.公路交通技术，2006，23（3）：163－166.

［6］ 张大海，汪世芳，史开泉.灰色预测公式的理论缺陷及改进［J］.系统工程理论与实践，2002，22（8）：1－3.

［8］ 赵志刚，常成.带变异算子的自适应粒子群优化算法［J］.计算机工程与应用，2011，47（17）：42－44.

［9］ 邓聚龙.灰理论基础［M］.武汉：华中科技大学出版社，2002.

［10］ 李松，刘力军，刘颖鹏.改进PSO 优化BP 神经网络的混沌时间序列预测［J］.计算机工程与应用，2013，49（6）：245－246.

［11］ 张飞涟，史峰.铁路客货运量预测的随机灰系统模型［J］.中南大学学报，2005，36（1）：159－159.

［12］ 张燕，王繁珍，陈增强，等.基于递归神经网络的多变量系统预测控制［J］.南开大学学报，2006，39（1）：49－53.

［13］ 王庆荣，张秋余.基于随机灰色蚁群神经网络的近期公交客流预测［J］.计算机应用研究，2012，29（06）：2080－2084.