基于最近邻子空间搜索的两类文本分类方法*
2015-03-19李玉鑑冷强奎
李玉鑑,王 影,冷强奎
(北京工业大学计算机学院,北京100124)
1 引言
文本分类是指用计算机按照一定的标准对文本集自动赋予类别标记,它在信息检索、文本挖掘和舆情分析等领域中具有重要应用,其中涉及文本表示、特征选择、分类模型和评价方法等关键技术[1,2]。
目前,比较常用的文本分类器有朴素贝叶斯(Naive Bayes)、支持向量机SVM(Support Vector Machine)、K 最 近 邻KNN(K Nearest Neighbor)[3]等。最近邻方法是KNN 的一个特例,基本思想是在训练集中找到测试样本的最近邻样本,然后根据此最近邻样本的类别作出决策。但是,最近邻方法只根据距离最近原则进行分类,分类精度易受噪声数据的干扰。而且,如果训练集文档数量较大,对新样本分类就需要较大的计算开销,从而导致分类过程较慢。本文利用最近邻子空间搜索[4]的思想可以在一定程度上克服最近邻方法的上述缺点。
目前,已存在一些利用子空间思想表示文本特征信息的算法,例如基于子空间聚类[5]以及随机子空间[6]的文本分类方法。基于子空间聚类的文本分类方法中,每个特征维度根据其对区分不同类别文本的贡献程度的大小被赋予不同的权重,基于这些维度权重,能够在一个加权的高维空间中完成文本的聚类过程。随机子空间方法将特征空间划分为若干个维度较低的特征子空间,然后在每个维度较低的特征子空间上进行分类,最后合并结果。这些方法都能够有效地降低特征空间的维度,充分证明了以子空间表示文本特征信息的优越性。
最近邻子空间搜索是一种新近提出的模式分析方法,已在模式识别、机器视觉和统计学习[7,8]等领域获得了成功应用。它的基本思想是选择一组向量构成的子空间来表示同类或相关数据的重要信息,再把这组向量映射成高维空间中的点,最后再通过高维空间中的最近邻方法解决所涉及的问题。子空间在计算机视觉和模式识别中是一种常用的信息表示方法。例如,在计算机视觉领域中,子空间常常用来表示不同光照、视角和空间变化下的物体特征。当一幅(或多幅)给定的查询图像被表示为高维空间中的点(或子空间)时,就可能需要从一个子空间数据库中搜索与其最近的子空间。而解决相关问题的一种有效方法就是最近邻子空间搜索。
本文的目的是将最近邻子空间搜索的思想应用于文本分类领域,大体思路如下:首先用向量表示文本,用子空间表示文本的类别特征信息,然后把类别子空间和查询向量映射为高维空间中的点,最后利用最近邻算法完成分类过程。最近邻子空间搜索的本质是在高维空间中用最近邻点搜索计算与查询向量距离最近的类别子空间。由于实际上只需要计算高维空间中的向量距离,因此能够简化分类过程,提高分类效率。
本文组织结构如下:第2节简要介绍最近邻子空间搜索方法;第3节为文本的子空间表示;第4节统计在标准数据集上的实验结果,最后是结束语。
2 最近邻子空间搜索简介
本文把子空间定义为一个相互正交的向量集合。包含k个n维向量的子空间S可以用一个n×k维的矩阵表示。给定一个n维向量构成的子空间集合{S1,S2,…,Sm}和一个查询向量q∈Rn,相应的最近邻子空间问题是计算与q距离最近的子空间S*,即:

其中,dist(q,Si)表示q与Si之间的欧氏距离。
设S是一个n×k维矩阵表示的子空间。显然,直接计算dist(q,S)比较困难。为了简化最近邻子空间的计算,可以先定义两个函数变换,即u=f(S)和v=g(q),分别将S和查询点q映射到同一高维空间内的点u、v∈,其中n′表示高维空间的维度。然后,在空间内搜索点v的最近邻点,并作出决策。不过这两个函数变换必须保证u和v的距离‖u-v‖ 与原空间Rn中查询点q与子空间Si的距离dist(q,Si)保持同步单调性,即满足下式:
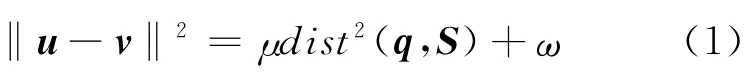
其中,μ、ω为某一特定值的常数,使得映射前后的两个距离呈线性关系。最近邻子空间搜索的映射模型如图1所示。其中,图1a表示在原空间中的查询点和各个子空间,图1b表示经过映射后的点。

Figure 1 Mapping model of nearest subspace search图1 最近邻子空间搜索的映射模型
在公式(1)成立的情况下,最近邻子空间的搜索问题就可以转化为高维空间中的最近邻搜索问题。
为了方便地描述整个映射过程,首先为任意n×n的对称矩阵M=(mij)定义一个映射h如下:

显然,h的作用是把矩阵M映射为一个n′=n(n+1)/2维的列向量。这个列向量由矩阵M的上三角部分按行连接构成,且对角线上的元素乘以常数因子
设I为单位矩阵。如果令那么前面提到的f和g可以定义如下:

其中,

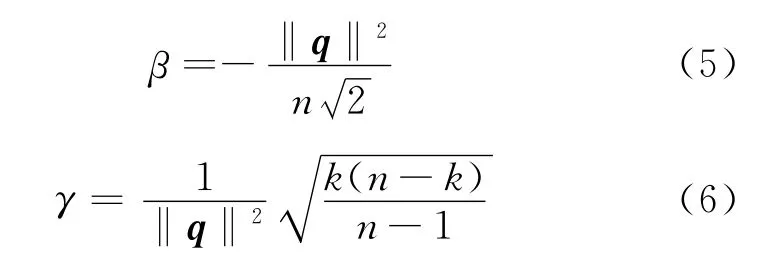
公式(2)~公式(6)的证明可参见Basri R 等人[4]的论文。根据这些公式还可以确定公式(1)中的μ和ω如下:

利用式(2)和式(3),就能够将Rn中的子空间S和查询向量q映射为空间中点u和v。因此,只需在空间中对点v进行最近邻搜索,就可以实现Rn中的最近邻子空间搜索。
3 文本的子空间表示
为了构建文本的子空间,首先需要对文本进行特征向量表示,然后由得到的特征向量构建不同类别文本的子空间。其中,为将文本表示为特征向量,需要经过特征提取和特征项赋权两个步骤。下面逐一介绍本文中采用的特征提取、特征项赋权以及子空间构建方法。
3.1 特征提取
特征提取即按照一定的约束条件,从词项集合中选取词项子集的过程。选择的约束条件不同,特征提取方法也不同。常用的特征提取方法有基于文档频率、基于CHI统计等。本文中采用CHI统计完成文本的特征提取过程。
CHI方法假设特征t与文本类别ci之间的非独立关系类似于具有一维自由度的χ2分布,t对于ci的CHI值由下式计算:

其中,N表示训练语料中的文档总数,ci为某一特定类别,t表示特定的词项,A表示属于ci类且包含t的文档频数,B表示不属于ci类但是包含t的文档频数,C表示属于ci类但是不包含t的文档频数,D是既不属于ci也不包含t的文档频数。
CHI方法不仅考虑到了特征项与类别的正相关对特征项重要程度的影响,而且也考虑了特征项与类别的反相关对特征项重要性的影响。如果特征项t和类别ci正相关,说明含有特征项t的文档属于ci的概率要大一些;如果特征项t和类别ci反相关,就说明含有特征项t的文档不属于ci的概率要大一些。
3.2 特征项赋权
对文本进行分类之前,需要将文本表示为计算机能够处理的形式。向量空间模型是使用较多且效果较好的表示方法之一[9],在该模型中,文档空间被看作是由一组正交向量张成的向量空间。如果选择了n个特征项tk,且文本d关于特征项tk的权值为ωk,那么文本d可以表示成向量d=(ω1,ω2,…,ωn)。
本文采用词频关频积tf·rf(Product of Term Frequency and Relevance Frequency)的赋权值方法,其中tf是词频,rf是相关频率[10]。对于词项tk,令文本d关于tk的权值为ωk,产生文本d的向量表示d=(ω1,ω2,…,ωn)。根据tf·rf计算权值ωk的公式描述如下:
ωk=tfk*rfk
其 中,tfk表示词项tk在文档d中的频率,rfk的计算公式如下:

其中,ak表示包含词项tk的正类文本数,ck表示包含词项tk的负类文本数。
3.3 子空间构建
通过对文本特征提取和特征项赋权的过程,我们可以得到每个文本的向量表示。在此基础上,为完成最近邻子空间搜索过程,我们需要构建代表性强、区分度大的子空间,它能够直接决定分类效果的优劣。本文中采用奇异值分解来提取两类样本的子空间信息。奇异值分解是一种有效的矩阵特征提取方法,矩阵的奇异值反映了矩阵向量间的内在代数本质,具备良好的数值稳定性和几何不变性,它在语音识别、图像处理、控制论等众多领域有着重要应用[11,12]。
设M为n×m非零矩阵,如果矩阵的秩r(M)=r≤min(n,m),那么关于M存在下面的奇异值分解:
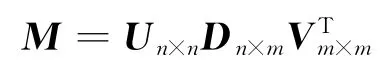
其中,Un×n、Vm×m是 正 交 矩 阵,Dn×m=(Dr,O)(n≤m)或Dn×m=(Dr,O)T(n≥m),O为零矩阵,Dr=diag(σ1,σ2,…,σr)。σi称为M的奇异值,在矩阵Dr中按从大到小降序排列。事实上,i=1,2,…,r),且λi是MTM和MMT的非零特征值,λ1≥λ2≥… ≥λr>0。
如果选取最大的k个奇异值,可以得到M的近似奇异值分解Mk:

根据Eckart-Young定理,在所有秩不超过r的矩阵中,Mk与M之差的Frobenius范数最小。因此,当k越接近于r,则Mk越接近于M。
在文本分类时,如果M是某类文本向量构成的矩阵,那么选择合适的k对其进行近似奇异值分解(本文的所有实验均取k=22 完成),相应的矩阵Un×k就是该类文本的子空间,其中n为文本特征项的个数,也就是特征维数。对于两类文本分类问题,分别构造正类和负类文本的两个子空间,通过计算待分类文本的查询向量与它们之间的最近距离,实际上只需计算它在高维空间中的映射向量与两个子空间的映射向量之间的欧氏距离,就可以完成分类过程。虽然多类问题在理论上可以类似处理,但是本文只考虑两类问题,因为用公式(7)计算相关频率只对两类问题效果较好,而不能直接用于多类问题。
4 实验
本文 采 用Reuters-21578 数 据 集[13]中 文 本 数目 最 多 的 前10 类 文 本,包 括acq、corn、crude、earn、grain、interest、money-fx、ship、trade、wheat。实验中共使用68 274篇文本,其中65 740篇作为训练集,其余的2 534篇作为测试集。
在每次分类过程中,均指定某一类样本作为正类样本,将其余的9类样本作为负类样本,共完成了10组实验。数据集描述及经过特征选取后特征维数如表1所示。

Table 1 Descriptions of data sets used in the experiments表1 实验中数据集描述
4.1 性能评价
分类器的性能主要采用正确率(Accuracy)、准确率(Precision)、召回率(Recall rate)和F1 值作为评价指标。正确率是指分类器正确分类的样本数与总样本数之比。准确率(查准率)是指分类器正确分类的正样本数与分类器分为正类的总样本数之比。召回率(查全率)是指分类器正确分类的正样本数与实际正样本数之比。F1值是准确率与召回率之间的综合指标,定义如下:
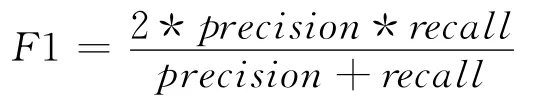
为了分析基于子空间映射的文本分类方法的可行性以及有效性,我们将该方法与基于传统的最近邻搜索方法进行了对比实验。
4.2 实验结果
本文利用正确率、准确率、召回率和F1 值作为评价指标,并记录实验中整个文本分类过程耗费时间。在Reuters数据集上对最近邻子空间搜索与最近邻搜索进行文本分类获得的比较实验结果如表2所示。
从表2可以看出,在选定不同的类作为正类的情况下,用最近邻子空间搜索进行文本分类的三项指标普遍优于最近邻搜索。当ship作为正类时,因为数据的不平衡性,最近邻搜索将所有的样本都分为负类,因此准确率无法计算,召回率为0,导致F1值无法计算。所以,在计算最近邻搜索的各个评价指标的平均值时,不考虑该组数据。从表2中可以看出,无论数据样本的平衡与否,最近邻子空间搜索的平均正确率为93.4%,平均召回率为84.1%,以及平均F1值为0.588 8,充分证明了它比最近邻搜索在分类总体性能上具有明显优势。
此外,表2还记录了用最近邻子空间搜索进行文本分类所需的总时间,包括读数据、映射和分类等过程,平均耗时1 603s。由于最近邻搜索耗时较长,最短的也需要53 700s,所以在此未对相应的时间进行详细记录。因此,最近邻子空间搜索不仅在总体上能够获得更好的分类性能,还可以有效地减少所需的计算时间。
5 结束语
本文中将最近邻子空间搜索应用于文本分类问题,与最近邻搜索相比,既能获得整体分类性能上的提高,又能有效地减少整个分类过程所需的计算时间。而且,最近邻子空间搜索还能够在一定程度上避免分类过程中对单个文本类别的依赖,通过利用每类文本的子空间表示其类别特征信息,提高对噪声样本的抗干扰能力。

Table 2 Comparison of nearest neighbor search and nearest subspace search on accuracy,precision,recall rate and F1value表2 最近邻搜索和最近邻子空间搜索在分类正确率、召回率和F1值上的对比实验
[1] Debasena C L,Hemalatha M.Automatic text categorization and summarization using rule reduction[C]∥Proc of IEEE Conference Advances in Engineering,Science and Management,2012:594-598.
[2] Cai Yue-hong,Zhu Qian,Cheng Xian-yi.Semi-supervised short text categorization based on random subspace[C]∥Proc of the 3rd International Conference on Computer Science and Information Technology,2010:470-473.
[3] Yang Y,Liu X.A re-examination of text categorization methods[C]∥Proc of the 22nd Annual International ACMSIGIR Conference on Research and Development in Information Retrieval,1999:42-49.
[4] Basri R,Hassner T,Zelnik-Manor L.Approximate nearest subspace search with applications to pattern recognition[C]∥Proc of IEEE Computer Society Conference on Computer Vision and Pattern Recognition,2007:1-8.
[5] Ahmed M S,Khan L.SISC:A text classification approach using semi supervised subspace clustering[C]∥Proc of IEEE International Conference on Data Mining Workshops,2009:1-6.
[6] Mehrdad J G,Mhamed S K,Robert P W.Random subspace method in text categorization[C]∥Proc of the 20th IEEE International Conference on Pattern Recognition,2010:2049-2052.
[7] Basri R,Hassner T,Zelnik-Manor L.A general framework for approximate nearest subspace search[C]∥Proc of the 12th IEEE International Conference on Computer Vision Workshops,2009:109-116.
[8] Wright J,Yang A,Granesh A,et al.Robust face recognition via sparse representation [J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2009,31(2):210-227.
[9] Salton G.Introduction to modern information retrieval[M].New York:McGraw Hill Book Company,1983.
[10] Man L,Chew L T,Jian S,et al.Supervised and traditional term weighting methods for automatic categorization[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2009,31(4):721-735.
[11] Berry M W,Dumais S T.Using linear algebra for intelligent information retrieval[J].SIAM Review,1995,37(4),573-595.
[12] Liu Gui-long,Wang Hui-ling,Song Rou.Application of matrix singular value decomposition(SVD)to the research of text categorization on style[J].Computer Engineering,2002,28(12):17-19.(in Chinese)
[13] Bache K,Lichman M.UCI machine learning repository[EB/OL].[2013-4-20].http://archive.ics.uci.edu/ml.
附中文参考文献:
[12] 刘贵龙,王慧玲,宋柔.矩阵的奇异值分解在文本分类研究中的应用[J].计算机工程,2002,28(12):17-19.
