蒸发波导条件下海上超视距通信距离研究*

张海勇，周 朋，徐 池，卢宝峰

(1.海军大连舰艇学院 通信系，辽宁 大连116018;2.解放军91404 部队，河北 秦皇岛066001;3.解放军91991 部队，浙江 定海316000)

1 引 言

电磁波在大气环境中传播，受大气折射影响会发生弯曲，弯曲程度达到一定条件，会发生陷获折射现象。当大气中出现陷获折射时，满足一定条件的电磁波会被限制在一定厚度的大气层内经上下边界来回反射向前传播，就像在金属波导管中传播一样，这种现象称为大气波导，形成波导传播的大气层称为波导层［1］。大气波导通常分为三类:表面波导、悬空波导、蒸发波导。蒸发波导由于其出现概率大且一般发生在40 m以下高度的近海面大气中，对舰载电子系统产生较大影响。目前，国内外对蒸发波导研究比较深入，已形成多套成熟的蒸发波导预测模型［2－8］，但在实际应用中多集中于雷达探测系统［9－10］，在通信方面应用较少。本文针对蒸发波导这一特殊的大气现象，根据电磁波形成波导传播的性质变化，研究蒸发波导条件下实现海上微波超视距通信的有效通信距离。

2 蒸发波导及电磁波超视距传播

2.1 蒸发波导特征

蒸发波导是由于海面水汽蒸发使湿度在很小的垂直高度内发生锐减而形成的一类特殊的大气波导。图1为蒸发波导大气修正折射指数示意图，波导厚度为d，由于海表面几十米高度上水汽含量低，因此海面水蒸气压力递减，从而使修正折射指数M随高度递减，到达一定高度后，水蒸气分布又使修正折射指数达到最低点后随高度增加，最低点所在高度即为蒸发波导高度。因此，要预测蒸发波导高度，首先要有可靠的大气修正折射指数轮廓剖面。

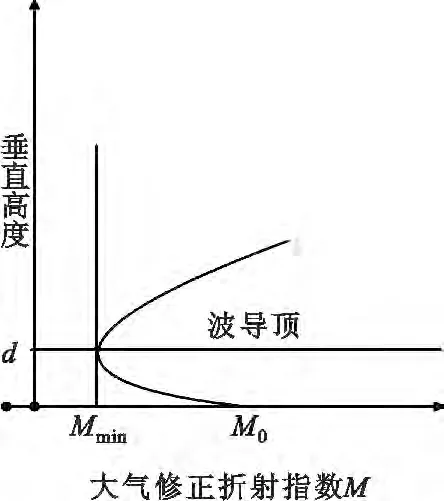
图1 蒸发波导大气修正折射指数Fig.1 Atmospheric correction refractive index contour of evaporation ducting

电磁波在大气环境中传播，主要受大气折射率n 的影响，通常引入大气折射指数N 来表示电磁波的折射特征，折射指数N =(n－1)×106，大气折射指数N 的表达式如下:

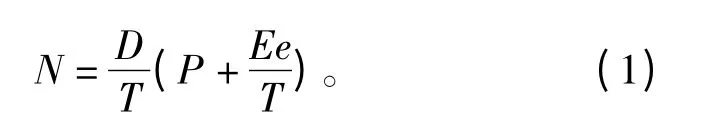
式中，D、E 为经验常数，P 为气压，T 为气温，e 为水汽压。为忽略地球表面影响，蒸发波导结构可用大气修正折射指数M 来表征，M 表达式为

式中，z 为地面以上高度。

由上式可以看出，只要获取海上各个高度上温度、气压和水汽压，就可以确定大气修正折射指数轮廓，大气修正折射指数最小值点所对应的高度即为蒸发波导高度。然而直接获取上述参数难度大且探测设备存在缺陷，国内外通常采取利用水文参数计算模型或实测数据反演算法预测蒸发波导。目前，应用较为成功的蒸发波导预测模型是由美国的Paulus－Jeske 提出并不断修正的P－J 模型［8］，此模型得到的大气修正折射指数表达式为

式中，Z0为海面粗糙度参数;Φ 为普适函数，不同大气层结下表达式不同;为层结稳定度参数，大于零时层结是稳定的，小于零时层结是不稳定的，等于零时层结是中性的。

2.2 电磁波形成超视距传播条件

蒸发波导能够将电磁波陷获在波导层内，从而使电磁波以较少的损耗向前传播，形成电磁波的超视距传播，传播距离达到正常情况下的数倍或更远。能够形成波导传播的电磁波在电磁波频率选择及发射仰角上存在一定的限制条件［10］，即电磁波频率必须大于某一特定频率，此频率称为最低陷获频率fmin，fmin与大气修正折射指数梯度和大气波导厚度d满足如下关系:

对公式(4)利用计算机仿真得到结果如图2所示。取平均大气修正折射指数梯度为－0.5，图2描述了最低陷获频率随波导高度的变化曲线。可以看出，受蒸发波导影响的主要是微波频段的通信，波导高度越高所能陷获的电磁波最低频率越低。

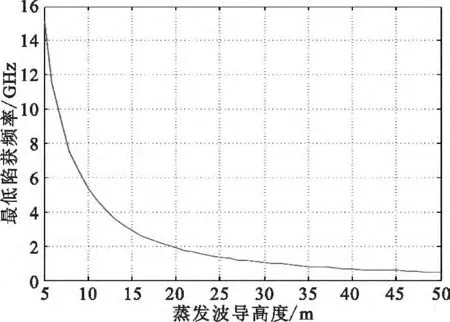
图2 最低陷获频率随波导高度变化曲线Fig.2 Minimum trapping frequency versus height of ductin

电磁波的入射仰角必须要小于某一临界入射角Φc，Φc与波导强度满足如下关系:

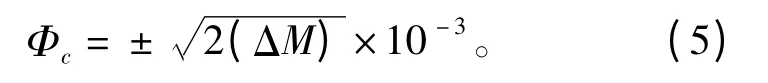
式中，ΔM 称为波导强度，ΔM=M0－Mmin。

临界入射角随波导强度变化曲线仿真结果如图3所示，临界入射角一般较小，约1°，因此，只有与波导边界夹角较小的电磁波才能形成波导传播;在满足波导传播的条件下，电磁波临界入射角随波导强度增大而变大，临界入射角越大，所能捕获的电磁波范围越大。

图3 临界入射角随波导强度变化曲线Fig.3 The critical angle of incidence versus intensity of ducting

3 蒸发波导条件下超视距通信距离估算方法

3.1 电磁波传播损耗

蒸发波导的电磁波传播损耗由两部分组成:一是自由空间传播损耗，二是由媒质对电磁波的吸收以及障碍物对电磁波的散射、反射和绕射等作用引起的损耗［11］。传播损耗记为L，自由空间传播损耗为Lf，媒质的传播损耗为A，传播损耗可以表示为

自由空间的传播损耗Lf为发射天线的辐射功率Pt与接收天线的最佳接收功率Pr的比值，即

由电磁波传播理论可以得到

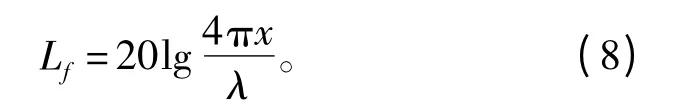
式中，λ 为电磁波波长，x 为电磁波的传播距离。

媒质的传播损耗A 是传播因子F 的函数，满足

传播因子的定义为

式中，E 和E0分别表示接收点的场强以及自由空间接收点的场强。蒸发波导环境下传播因子F 可由下式计算:

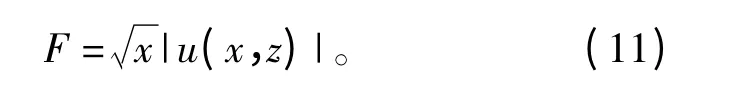
式中，x 和h 分别代表电磁波的传播距离和高度，u(x，z)表示距离x 高度z 处的场强。

因此，蒸发波导条件下电磁波的传播损耗为

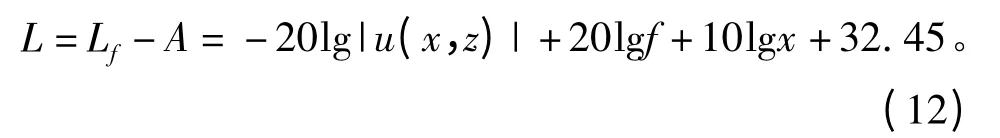
电磁波在某一点的电场强度难以精确计算，通常采用抛物线方程的方法描述电磁波在大气波导中的轨迹，计算电磁波某点场强的抛物线方程为

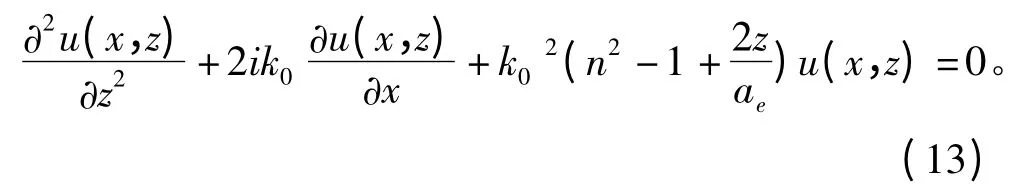
在求解抛物线方程时，需给定初始场及上下边界条件，目前可采用的方法有分布傅里叶方法和离散混合傅里叶算法［12］，本文给出分布傅里叶方法求解结果。抛物线方程的分布傅里叶解可表示为

式中，Δx 为水平方向的步长，u(x0，z)为初始场分布，k0为自由空间波数，k0=ω/c，p =k0sinθ，θ 是传播方向与水平面间的夹角，F、F－1分别表示傅里叶变换和傅里叶逆变换。利用抛物线方程求得空间电磁波场强的傅里叶解，进而定量估算出蒸发波导下电磁波的传输损耗，为下一步计算电磁波超视距通信距离打下基础。

3.2 蒸发波导超视距通信距离估算方法

研究表明:受蒸发波导影响的电磁波一般是频率较高的微波［13］，本文对电磁波形成波导传播条件的仿真结果也对此进行了进一步的验证。微波信号通信模式为［14］

式中，Pr为天线的接收功率(单位dBW)，Pt为对端的发射功率(单位dBW)，G =Gr+Gt为两端天线增益和系统增益之和(单位dB)。因此，在蒸发波导条件下微波信号接收功率表达式为

式中，Ls为馈线损耗等其他损耗之和。由上式可得超视距通信距离R 的表达式为

当接收机的接收功率等于门限接收电平Pr0时，对应的通信距离为最大有效通信距离，将波长λ 用频率f 表示，可得到最大有效通信距离dmax的表达式如下:

门限接收电平Pr0与归一化信噪比Es/N0、接收机噪声系数NF及环境温度T0存在如下关系:

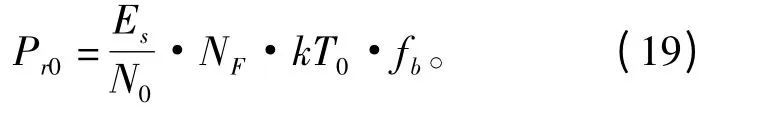
式中，k 为玻尔兹曼常数，fb为数字信息的比特率。

利用电磁波传输损耗，门限接收电平以及电磁波传播因子通过上式计算即可获得蒸发波导条件下超视距通信的有效通信距离，计算流程图如图4所示。

图4 流程图Fig.4 Flow chart of calculating effective communication distance

首先利用海洋气象环境参数确定大气修正折射指数轮廓剖面，根据蒸发波导预测模型计算蒸发波导高度、强度等信息，求解电磁波形成波导传播模型的抛物线方程，进而定量估算出蒸发波导的电磁波传输损耗:结合微波通信接收端接收电平计算公式及完成有效通信满足条件，得到蒸发波导超视距通信覆盖距离。

4 仿真分析

本文利用在研究蒸发波导环境下电磁波传播特征中较为常用的抛物线方程的方法，不同之处在于与结合微波频段通信的通信模式研究超视距通信距离的估算方法，对上述推导过程进行计算机仿真，得到不同波导高度电磁波传播损耗变化曲线如图5所示，发射天线方向图函数取1，电磁波传播速度c=3×108m/s，根据电磁波形成波导传播的条件，选取发射频率f =3 GHz，发射仰角为0.5°，电磁波传播距离为0～300 km，选取蒸发波导高度分别为20 m、25 m、30 m，上述参数选取与实际环境较为接近。为方便进行傅里叶变换及傅里叶反变换，假设修正折射率m 为常数，但在实际大气环境中m 是传播距离x 和所在高度z 的函数，实际应用过程中应加以考虑。求解抛物线方程时选取下边界(z=0)是平滑的理想导体平面，即下边界条件如下:

实际下边界通常是有限传导表面，多采用阻抗边界条件。

电磁波传播损耗是蒸发波导陷获能力的客观反映，传播损耗越小，陷获能力越强。仿真结果表明，在其他条件一定的情况下，蒸发波导高度越高，电磁波传播损耗越小，对电磁波陷获能力越强，完成有效通信距离越大;当电磁波传播到一定距离后，传播损耗随距离增大变化缓慢，电磁波达到更远的传播距离，进而实现电磁波超视距传播，增大通信距离，提高超视距通信能力;发射信号经电波传播损耗后，仍大于接收机的接收最低要求功率时，认为可以达到通信目的，否则，不能达到通信目的。发射天线大多是方向性天线，天线方向图函数大于1，因此在实际通信过程中，可根据发射天线类型计算传播损耗，结果略有差异。

微波通信系统中，通常采用卡塞格伦天线，当发射天线频率为2 GHz、高度为3 m时，两端天线增益之和约为33 dB［15］。采用上述参数对公式(16)仿真，结果如图6所示，描述了接收机接收功率随通信距离的变化曲线，其中，取发射功率为25 dBW，两端馈线损耗为6 dB，微波接收机的门限接收电平为－90 dB。从图中可以看出，在满足接收机接收功率大于门限接收电平情况下，通信系统可以达到有效通信目的，接收功率恰好等于门限电平时对应位置即为最大距离;在其他条件一定的情况下，波导高度越高，电磁波传播距离越远，有效通信范围越大;只要选取适当的天线发射频率及电磁波发射仰角，利用蒸发波导可实现超视距通信，并定量估算出最大有效通信距离。

实际海上通信过程中，可根据实测蒸发波导高度、强度等信息，计算电磁波传输损耗进而预测最大有效通信距离。舰艇编队航行过程中，在有效通信距离范围内，舰队可以分散队形，无需中继就能够保证舰间实时通信，增大舰艇编队的灵活性，确保编队战术战法得以准确实施［16］;利用电磁波传播距离可提高我方反侦察抗干扰能力，我方在进行超视距通信时，敌方在远距离范围内也能够探测或截获我方信息，因此在实际海战场环境下，通信系统选取适当发射参数，得到我方恰好可完成通信且在敌方监测范围之外的电磁波传播距离，有效规避敌方干扰，或实施电磁管制，选取适当时机进行通信，并在此过程中利用蒸发波导超视距探测能力对敌方进行侦测。

5 结束语

本文根据蒸发波导条件下电磁波传播特性，提出了基于蒸发波导条件下海上超视距通信距离估算方法，定量估算出最大有效通信距离，仿真结果验证了蒸发波导条件下微波频段可实现远距离通信，通信覆盖范围可到达视距之外。本文研究对保障海上微波超视距通信可靠性、提高通信系统应用能力具有重要指导意义。在实际应用中可进行微波超视距通信有效通信距离的估算，对于复杂气象环境下的通信距离可进一步研究。

［1］ 王海华.大气波导环境中电波传播特性及其应用研究［D］.西安:西安电子科技大学，2006.WANG Haihua.Research on Tropospheric Duct Propagation and Its Applications［D］. Xi'an:Xidian University，2006.(in Chinese)

［2］ 戴福山，李群，董双林，等. 大气波导及其军事应用［M］.北京:解放军出版社，2002:140－160.DAI Fushan，LI Qun，DONG Shuanglin，et al. Ducting and Its Military Applications［M］.Beijing:PLA Publishing House，2002:140－160.(in Chinese)

［3］ 焦林，张永刚，张宇.利用卫星数据反演海洋蒸发波导的研究［J］.海洋技术，2007，26(4):58－61 JIAO Lin，ZHANG Yonggang，ZHANG Yu. Research on Retrieving Oceanic Evaporation Duct with Application of Satellite Data［J］.Ocean Technology，2007，26(4):58－61.(in Chinese)

［4］ 焦林，张永刚.基于中尺度模式MM5 下的海洋蒸发波导预报研究［J］.气象学报，2009，67(3):382－387.JIAO Lin，ZHANG Yonggang.An evaporation duct prediction model coupled with the MM5［J］.ACTA Meteorologica Sinica，2009，67(3):382－387.(in Chinese)

［5］ Jeske H. The state of radar－ range prediction over sea［C］//NATO－ AGARD Conference Proceedings. Paris，France:［s.n.］:1971:1－10

［6］ Musson－Genon L，Gauthier S，Bruth E.A simple method to determine evaporation duct height in the sea surface boundary layer［J］.Radio Science，1992，27(5):635－644

［7］ Paulus R A. Practical application of an evaporation duct model［J］.Radio Science，1985，20(4):887－896

［8］ 漆随平，王东明，郭颜萍，等. 海上蒸发波导的预测方法综述［J］.海洋通报，2012，31(3):347－353.QI Suiping，WANG Dongming，GUO Yanping，et al.Overview on the methods of analysis and prediction on evaporation ducts over sea［J］.Marine Science Bulletin，2012，31(3):347－353.(in Chinese)

［9］ 黄小毛，张永刚，王华，等. 大气波导对雷达异常探测影响的评估与实验分析［J］. 电子学报，2006，36(4):722－725.HUANG Xiaomao，ZHANG Yonggang，WANG Hua，et al.Evaluation and Experimental Analysis of Radar Anomalous Detection Influenced by Atmospheric Ducts［J］.Acta Electronica Sinica，2006，36(4):722－ 725. (in Chinese)

［10］ 皇甫一江. 蒸发波导条件下雷达超视距探测距离研究［J］.现代雷达，2013，35(6):1－4.HUANGFU Yijiang. A Study on Radar Detection Range in Evaporation Duct Conditions［J］. Modern Rader，2013，35(6):1－4.(in Chinese)

［11］ 杨超.大气波导中电磁波传播及反演关键技术［D］.西安:西安电子科技大学，2010:36－37.YANG Chao.Electromagnetic Wave Propagation in the Atmospheric Duct and the Key Techniques of Inversion［D］.Xi'an:Xidian University，2010:36－37.(in Chinese)

［12］ Zhang Jinpeng，Wu Zhensen，Wang Bo，et al. Modeling low elevation GPS signal propagation in maritime atmospheric ducts［J］. Journal of Atmospheric and Solar－Terrestrial Physics，2012(3):12－15.

［13］ 张瑜，吴少华.大气波导传播类型及特性分析［J］.电波科学学报，2009，24(1):185－190.ZHANG Yu，WU Shaohua.Analysis of types and characteristics of atmospheric duct Propagation［J］. Chinese Journal of Radio Science，2009，24(1):185－ 190.(in Chinese)

［14］ 李海涛，李燕，张建忠. 微波定向天线对准实现方法［J］.无线电工程，2011，41(3):44－46.LI Haitao，LI Yan，ZHANG Jianzhong.Realization Methods for Microwave Directional Antenna Pointing［J］.Radio Engineering，2011，41(3):44－46.(in Chinese)

［15］ 郑林华，丁宏，向良军. 现代通信系统［M］. 北京:电子工业出版社，2010:16－17.ZHANG Linhua，DING Hong，XIANG Liangjun. Modern communication system［M］.Beijing:Publishing House of Electronics Industry，2010:16－17.(in Chinese)

［16］ 周朋，张海勇，贺寅，等.大气波导在海上通信中的应用［J］.电讯技术，2014，54(8):1134－1139.ZHOU Peng，ZHANG Haiyong，HE Yin，et al. Application of Atmospheric Duct in Maritime Communications［J］. Telecommunication Engineering，2014，54 (8):1134－1139.(in Chinese)