任意均分间隔的预失真结构*

刘庆杰，陈金树，盛 涌

(清华大学 电子工程系，北京100084)

1 引 言

在数字通信中，调制器是一个重要的组成部分。随着传输速率的提高，调制器输出信号的失真越来越明显，消除调制器输出信号的失真将成为一个亟待解决的问题。预失真技术可以有效减小调制器输出信号失真，很大程度上改善信号通过调制器后的质量［1－2］。

基带预失真器有两个重要特点，一是预失真算法，二是预失真器的结构。20世纪60年代Widrow和Hoff 提出了Least Mean Square(LMS)算法，随后又有Recursive Least Square(RLS)算法被提出。对于码元间隔均衡来说，当接收滤波器与信道输出的失真相匹配时，这种滤波器抽头间隔是最佳的［3］，但其无法补偿信道的频率畸变。1970年，Brady等［4］提出的分数间隔均衡器解决了这一问题。但是对于全数字调制器，调制前会有升采样，如果使用码元间隔或者分数间隔结构，滤波前必须重采样，而且预失真结果并不理想。针对这一问题，本文提出任意均分间隔结构的预失真器，无需重采样，直接对升采样后的数据自适应滤波，更准确地反映了调制器信道的特性，获得了更好的预失真效果。

2 调制器信道分析

卫星的调制器的失真主要由数模转换器(DAC)、重构滤波器和中频模拟卡等器件引起的，可以用一个线性失真信道代替。图1是某全数字高速调制器中心频率设为1200 MHz时信道的幅频特性曲线图和群时延特性曲线图的实测图，此时等效信道的带宽为660 MHz，即信道的带内范围是870～1530 MHz。

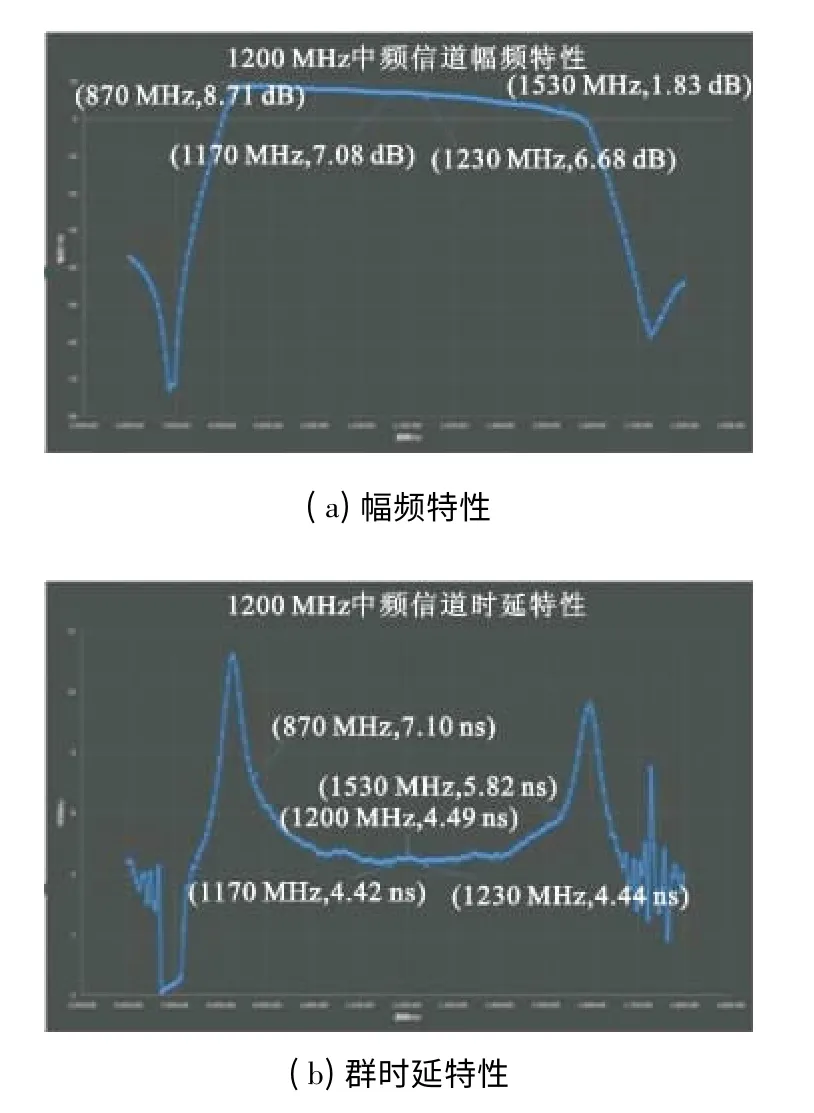
图1 1200 MHz 中频信道的幅频特性和群时延特性Fig.1 Amplitude－frequency characteristics and group delay characteristics of 1200 MHz intermediate frequency channel

由图1可以看出，高速调制器的1200 MHz中频的信道失真较为明显，仅从660 MHz的带宽内的幅度增益来看，频带最左侧的870 MHz处的幅度增益是8.71 dB，频带最右侧的1530 MHz处的幅度增益是1.83 dB，幅度增益呈下降趋势，带内最左侧与最右侧相差6.88 dB。而对于信道的群时延失真，频带最左侧870 MHz 处的群时延是7.10 ns，频带中心1200 MHz处的群时延是4.49 ns，频带最右侧的群时延是5.82 ns，即频带最左侧距离中心群时延相差2.61 ns，频带最右侧距离中心相差1.33 ns，对于符号率为330 Msample/s的信号来说，频带最左侧距离频带的中心的群时延差为0.861 3个码元。随着通信符号率的增加以及信道带宽的增加，群时延失真对通信质量的影响将越来越大。

3 预失真结构

3.1 码元间隔滤波和分数间隔滤波

根据输入滤波器信号的采样速率来分，滤波器的结构可以分为码元间隔和分数间隔，码元间隔滤波器其输入信号按照码元的速率进行采样，分数间隔预失真器的输入信号的采样率大于码元速率。

如果信号经过调制器后的采样频率小于它的奈奎斯特频率，其频谱会发生混叠，加上预失真器之后调制器输出信号会发生频谱混叠，码元间隔结构的预失真器只能对混叠后的信号进行补偿，而信道的频率特性由于混叠而损失掉了。此时，码元间隔滤波无法补偿信道的频率畸变。而Brady 等［4］提出的分数间隔均衡器(Fractionally Spaced Equalization，FSE)可以有效地解决这一问题。一般地，FSE 采样间隔为MTb/N，其中M、N 都是整数，且M ＜N;Tb为码元宽度，最常用的分数间隔均衡器抽头间隔是Tb/2。输入信号按照Tb/2 速率采样，线性滤波器抽头间隔为Tb/2，输出时均衡器再以码元速率恢复输入的数据。

分数间隔滤波器的输入信号由于采样频率的提高避免了调制器信道引起的频谱混叠，同时接收信号的频谱中含有信号的频率函数，滤波器可以有效地补偿信道畸变。此外，分数间隔滤波对定时相位误差不敏感，可以大大改善滤波器对信道折叠谱效应引起的定时相位误差。

3.2 任意均分间隔滤波

定义输入滤波器的信号其采样间隔为αTb(0 ＜α≤1)，该滤波器间隔称为任意均分间隔滤波结构。码元间隔滤波(α =1)和分数间隔滤波(α为有理数)都可以看作是任意均分间隔滤波的特例。

全数字高速调制器中，信号会有一个升采样的过程，以匹配中频DAC 的频率。全数字高速调制器中产生的失真相对整个通信信道而言是比较小的，由2.1 节中的分析可知，在330 Msample/s符号率的信号下，最大群时延失真是0.86 个码元，而如果采用码元间隔滤波，将覆盖好几个码元的能量，这样会导致滤波效果不佳。由于升采样后，信号采用间隔不一定能满足MTb/N(M、N 为整数)，这时如果要使用分数间隔滤波，必须要重采样，这样无疑增加了处理的复杂度和消耗的资源。在这种情形下，任意均分间隔滤波就非常合适。

以1600 Mb/s采样率的中频DAC 为例，全数字高速调制器中的信号均要升采样到1600 Msample/s。对于一个6 阶的FIR 滤波器和320 Msample/s的信号，如果采用码元间隔滤波，码元之间的间隔为3.125 ns，覆盖前后3 个码元共9.375 ns的能量。如果使用任意均分间隔滤波，同等情形下可覆盖前后共3.75 ns的能量。而在前文中提到的全数字高速调制器中，带内最大的群时延差只有2.61 ns，小于码元间隔，如果使用码元间隔滤波，很难取得较好的效果。但是如果使用任意均分间隔滤波结构，0.625 ns的精度及3.75 ns的覆盖度对群时延失真均可以取得比较好的预失真效果。同时，任意均分间隔的结构也可以消除调制器信道中信号的频谱混叠，更好地反应信道的特点，达到更好的预失真效果。

任意均分间隔结构的难点在于，自适应更新的时候使用码元点处的误差来更新权系数才有意义。在码元间隔滤波的时候，每一次更新迭代都是码元点，所以每一次更新都是有意义的，而任意均分间隔滤波的时候，非码元点处的误差其实并没有实际的意义，并且非码元点处判决也是难以处理的。所以本文方案是，只在码元点处更新滤波器的系数，非码元点处不做处理。如果升采样后的数据没有码元点，找离码元点最近的那个点即可。

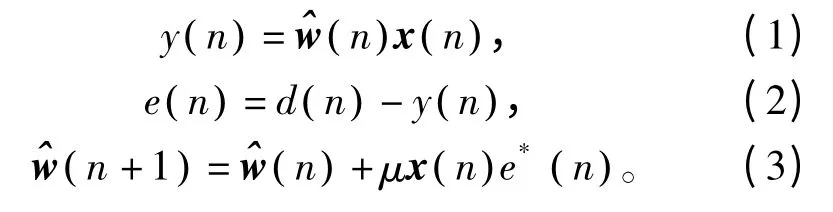
实际步长μ 取值范围是［6］为滤波器实际输入能量。LMS 算法优点在于运算量低，算法简单，但其收敛速度慢，且有额外误差。

以LMS 算法为例，码元间隔LMS 自适应滤波算法总结为如下三部分［6］:

滤波器输出:

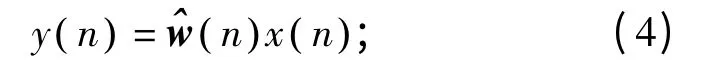
估计误差:

权系数自适应更新:

上面算法中，x(n)是码元间隔的，即是插值之前的数据。

任意均分间隔结构LMS 算法则有以下四个部分:

滤波器输出:

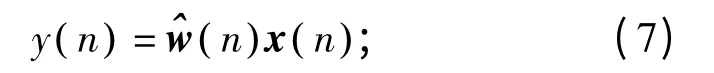
选择码元点:

估计误差:

权系数自适应更新:

上面算法中，x(n)是任意均分间隔的， ()y' m是码元间隔的数据，α 为前文中提到的均分间隔系数。任意均分间隔滤波器结构如图2所示。

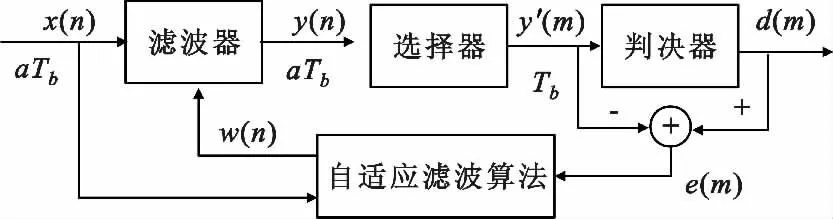
图2 任意均分间隔滤波器结构Fig.2 Arbitrary equationally spaced filtering structure

由前面的介绍可知，传统的码元间隔滤波和分数间隔滤波的输入和输出信号都是码元间隔的，而本文中提到的任意均分间隔滤波的输入与输出信号可以任意选择0 ＜α≤1 即可，一般可以根据升采样后码率来选择。

4 预失真仿真结果及实测效果

本节主要针对码元间隔滤波和本文提出的任意均分间隔滤波对调制器信道预失真的效果进行对比。

4.1 预失真Matlab 仿真结果

下面对QPSK 信号和32APSK 信号分别进行码间预失真和任意均分间隔预失真仿真，得到Matlab的仿真结果。实验中，调制器中心频率设为1200 MHz，QPSK 数据码率为640 Mb/s，32APSK 数据码率为1600 Mb/s(符号率均为320 Msample/s);数据不加成形滤波、低通滤波及内部信号均衡等措施。由于仿真时只是对一段数据作预失真，不像实时条件下的数据失真随时间变化，所以仿真得到的效果要略好于实测结果。

如表1所示，在资源耗费不变的情况下，码元间隔预失真将QPSK 原信号的质量提高了3.7 dB，而任意均分间隔预失真将QPSK 原信号质量提高了8.4 dB，这说明在QPSK 的调制方式下任意均分间隔预失真的效果要明显优于码元间隔预失真的效果。图3更为直观地显示了QPSK 不同结构预失真效果。

表1 QPSK 不同结构预失真器效果对比Table 1 Performance of different predistortion structures of QPSK signal

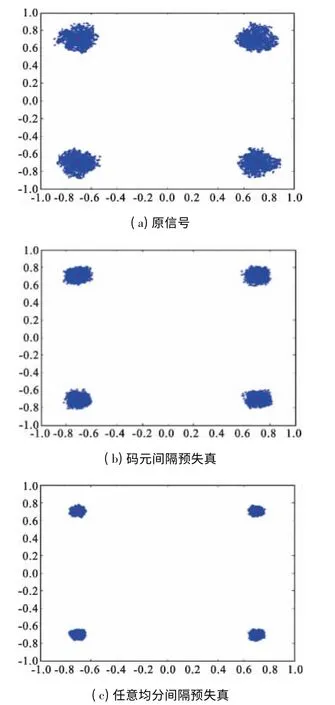
图3 QPSK 不同结构预失真效果Fig.3 Performance of different predistortion structures of QPSK signal

如表2所示，在资源耗费不变的情况下，码元间隔预失真将32APSK 原信号的质量提高了2.7 dB，而任意均分间隔预失真将32APSK 原信号质量提高了7.9 dB，这说明在32APSK 的调制方式下，任意均分间隔预失真的效果也明显优于码元间隔预失真的效果。图4更为直观地显示了32APSK 不同结构预失真效果。

表2 32APSK 不同结构预失真器效果对比Table 2 Performance of different predistortion structures of 32APSK signal

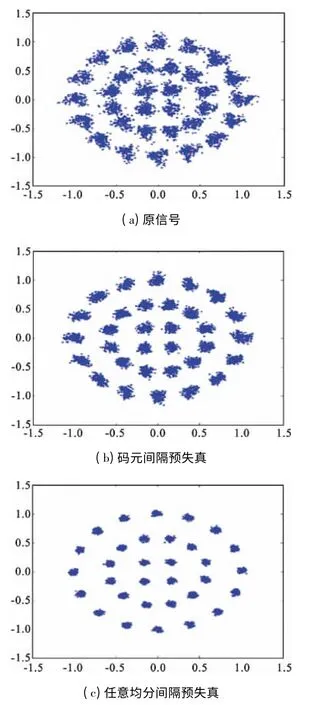
图4 32APSK 不同结构预失真效果Fig.4 Performance of different predistortion structures of 32APSK signal

从表1、表2和图3、图4中可以看出，无论是低阶调制方式还是高阶调制方式，任意均分间隔预失真结构对信号均能获得非常好的改善效果。

4.2 预失真实测结果

图5和图7是将预失真的模块加入到某全数字高速调制器之前，由Agilent 示波器中VSA 解调得到的结果，图6和图8是加入预失真模块后的结果，实验条件与仿真时相同。

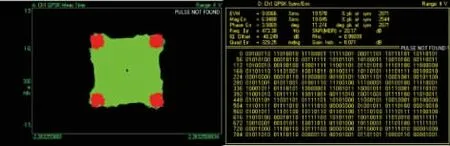
图5 QPSK 经过调制器信道后的失真图Fig.5 Distortion of QPSK output signal

图6 QPSK 任意均分间隔预失真实测效果Fig.6 Measured result of arbitrary equationally spaced filtering structure performance of QPSK signal

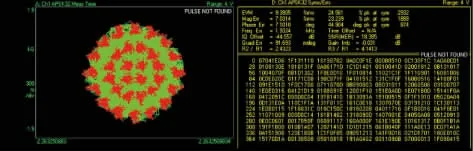
图7 32APSK 信号经过调制器信道后的失真图Fig.7 Distortion of 32APSK output signal

图8 32APSK 任意均分结构预失真实测效果Fig.8 Measured result of arbitrary equationally spaced filtering structure performance of 32APSK signal

从表3中可以看到，加入预失真模块后，QPSK信号的SNR 值提高了5.2 dB，32APSK 信号的SNR值提高了5.0 dB。从实际结果上看，加入任意均分间隔预失真模块后，信号的质量得到了明显提高，同时低阶的QPSK 调制方式和高阶的32APSK 调制方式均可以得到很好的预失真效果。

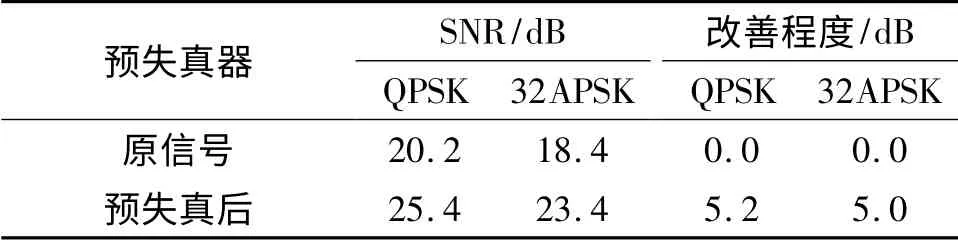
表3 实测预失真器改善效果Table 3 Measured results of predistortion performance

5 结束语

针对全数字高速调制器的特点，本文提出了任意均分间隔的预失真结构。Matlab 仿真和实测结果均表明，高码率下使用LMS 算法的任意均分间隔的预失真结构效果明显优于码元间隔预失真的结构。该结论对QPSK 及32APSK 等调制方式均适用，说明任意均分间隔的预失真结构与调制方式无关，都可以获得很好的预失真效果。此前文献中大多都是对预失真算法的改进，很少涉及到预失真器的结构，本文提出的新的预失真结构可取得比传统结构更佳的效果，无论在理论还是实用方面都具有很大的意义。下一步工作的重点应在于非线性预失真结构的研究及非线性预失真与线性预失真两种结构级联方法的研究。

［1］ 李凯，张科，张能波. Ka 频段10W 自适应射频预失真线性化固态功放研制［J］. 电讯技术，2014，54(7):958－963.LI Kai，ZHANG Ke，ZHANG Nengbo. Ka band 10W adaptive predistortion linearization of solid state power amplifier design ［J］. Telecommunication Engineering.2014，54(7):958－963.(in Chinese)

［2］ 郑金秀. 基于自适应基带预失真的高效率发射技术［J］. 电讯技术，2011，51(7):170－173.ZHENG Jinxiu. High Efficient Transmitting Technology Based on Baseband Predistortion for Satellite Communication［J］. Telecommunication Engineering，2011，51(7):170－173.(in Chinese)

［3］ 邱天爽，魏东兴，唐洪，等. 通信中的自适应信号处理［M］. 北京:电子工业出版社，2005.QIU Tainshuan，WEI Dongxing，TANG Hong，et al. Adaptive signal processing in communication［M］. Beijing:Publishing House of Electronics Industry，2005.(in Chinese)

［4］ Brady D M. An adaptive coherent diversity receiver for data transmission through dispersive media［C］//Proceedings of 1970 IEEE International Conference on Communication.San Francisco，CA:IEEE，1970:21－35.

［5］ Haykin S. 自适应滤波器原理［M］.4 版. 郑宝玉，译.北京:电子工业出版社，2010.Haykin S. Adaptive Filter Theory［M］.4th ed. Translated by ZHENG Baoyu. Beijing:Publishing House of Electronic Industry，2010.(in Chinese)

［6］ 张旭东，陆明泉. 离散随机信号处理［M］. 北京:清华大学出版社，2005.ZHANG Xudong，LU Mingquan. Discrete Random Signal Processing［M］. Beijing:Tsinghua University Press，2005.(in Chinese)