分布式数据链的定周期自适应时间对准*

田斌鹏，刘丽丽

(1.中国西南电子技术研究所，成都610036;2.解放军61660 部队，南京210001)

1 引 言

数据链的数据交互以周期性信息为主要数据，包括平台自身和目标数据通过周期性的播报形成战场态势信息。美军Link 16 从集中式处理发展到分布式航迹处理，各个节点需要完成各种数据的交互。为了保证同一时刻各成员获取的目标和平台信息的一致性，同时在同一时刻保证同一航迹在同一时间点只有一个担任报告职责的成员通报，因此需要将具有报告职责的节点通过对数据链中远端航迹与本地航迹数据进行关联、融合，使其可有效地形成有效航迹。航迹要与网内其他所有航迹作比较，当远端航迹和本地航迹的相关性比较差时，可能导致目标的报告存在误差，甚至出现网内不同的报告职责单元在同一时间对同一目标重复播报。因此，为了提高航迹的相关、改善融合结果，必须首先对各个报告职责单元的航迹进行校正，修正系统误差，有效提高误差水平，做到航迹不丢、不重、不乱、最佳［1］。

为了达到上述报告职责单元航迹高质量的融合，形成有效的数据，首先必须进行时间对准，否则，未对准的数据可能导致比单独使用任何一个平台报告数据都还差［2］。同时，为了能最大限度地提高多平台数据融合的优势，对各个平台报告时间进行时间对准是必不可少的。

多平台信息融合中的时间对准问题是数据链系统数据融合问题的关键技术之一［3］。该处理对数据实时性和相关性提高具有重要作用，对数据间存在的时差需要根据具体情况进行内插或者外推时间操作，实时校正系统间存在的实际误差，通过对各个节点报送信息的时间及导航信息的考察，有效地实现多节点信息节点数据对准，以对目标的观测建立实时有效目标航迹。

时间对准算法［4－6］的研究主流是处理多节点关联的基础工作，解决多节点时间不同步问题主要有基于统一时基的处理方法和基于插值的统一时间处理法。第一类算法的灵活性和对环境的适应性较差，无法满足系统偏差不固定情形;第二类算法的鲁棒性较差，当系统达到稳态时，增益趋于极值，将丧失对突变状态的跟踪能力，而且对初值的依赖性较大，可能存在发散等问题。最早的对准思想是，针对不同节点存在的差异，假设各节点均匀采样，利用采样周期之比，通过平滑算法，将各节点统一对准到统一时间上。针对移动平台，Dela 等［7］同时考虑了节点量测偏差和平台姿态偏差，他们首先在没有姿态偏差的假设前提下消除量测偏差，然后再消除姿态偏差，这种处理方式忽略了两种不同偏差之间的耦合关系，未考虑其时间的一致性和时间采样的不均匀性。

本文通过分析时间对准的原理，结合分布式数据链系统的特点，建立了时间对准模型，通过分析目标的典型运动，分析目标的对准结果，有效完成了分布式数据链系统时间统一。

2 基于定周期自适应的时间对准

2.1 数据链时间对准模型

分布式数据链采用无中心报告，数据链系统中各个平台节点对目标的测量是相互独立的，且采样周期一般不同，另外再加上传输延迟以及无线网络的可靠性因素，使各个平台推送目标信息时的时间或具有报告职责的节点收到的目标信息是不同的(如图1所示)，需要时间对准后才能进行融合处理。时间对准采用内插、外推、拟合等算法对各节点平台报告的观测序列进行统一处理，使得各平台能提供对同一目标同一时间的观测数据。在多源数据处理中，融合处理的各平台数据必须是同一时刻的，只有这样才能保证同一时间网内目标播报状态是最新的，才能计算出目标的正确状态。

图1 节点a 和节点b 采样时刻关系Fig.1 Sampling scale relation between node a and node b

假设数据链中有两个融合节点，分别为节点1和节点2，这两个节点的报告时隙分别为τ 和T，且两者之比为整数，即τ/T =n。该假设是合理的，因为从目标探测到到发送出去，一般都是固定时隙加探测时间。

如果节点1 对目标状态最近一次更新时间为(k－1)τ，下一次更新时间为k =［(k－1)τ +nT］;节点2 对目标状态最近一次更新时间为(k－1)T，下一次更新时间为kT，这意味着在连续两次目标状态更新之间，节点2 有n 次测量值。于是可采用最小二乘规则，将这n 次测量值融合成一个虚拟的测量值，作为后一时刻节点2 的测量值，再和节点1 的测量值进行融合。用Zn=(z1，z2，…，zn)T表示(k－1)至k 后时刻节点2 的n 个测量值集合，与k 时刻节点1 测量同步，U=［z，］表示z1，z2，…zn融合以后的测量值及其导数，则节点2 的测量值zi可以表示成

式中，vi表示测量噪声。将上式写成向量形式为

式中，Vn=［v1，v2，…，vn］T，

则可以根据最小二乘法进行目标的定位。

2.2 定周期自适应时间对准

分布式数据链系统的信息种类包括平台状态信息、自身位置信息、目标航迹信息等。由于以上信息的发送与探测时间、探测周期相关，不具备时间基准，而无中心的融合必须根据收到的信息进行时间统一。为了能及时处理、准确分发融合后的目标信息，本文采用定周期时间对准建立一种数据链信息自适应对准模型，具体算法流程见图2。

图2 时间对准流程Fig.2 Time－alignment process

根据数据链的特点完成时间对准，由于不同的平台和消息发送周期存在差异，假设平台发送消息的周期分别为{T1，T2，…，Tn}，则在融合前将信息融合确定到统一时间点上。时间对准点为

根据时间周期对准的特点，特别是实际数据链存在的网络环境，可能周期不是严格的规定的周期，为了计算方便和去除网络的影响，则设定其对准时间点为消息标准制定发送的周期。

为了对数据进行精确计算，可以采用卡尔曼滤波完成目标精确的对准。卡尔曼滤波相关知识不是本文研究的范围，在此不再给出详细的论述，具体可参见文献［2－3］。通过卡尔曼滤波可有效地使各个不同传感器数据都对准到同一时间点T 上，此时，通过坐标变化，假设其信息统一，则可以根据其报送的信息质量完成其融合。

3 数值试验

根据真值情况与测量误差和滤波后误差的数据进行对比分析，通过统计来有效完成该方法的测试。

3.1 试验场景设置

在通用PC 机(主频3 GHz、内存2 GB)上利用Matlab2009 仿真软件进行算法仿真，参数设置参照实际传感器探测周期进行合理设置，与真实场景相比，目标数比实际要少，但是多次实验表明，三目标对准与多目标对准算法上具有一致性，同时对真实3 类目标的运动行为进行考虑，因此设定场景如下:在空中数据链上，同时由于网络原因可产生一定的延迟。假设有3 类目标被3 个平台同时报告，模拟3 个目标在二维(X－Y)平面上做交叉运动，目标1做匀速直线运动，目标2 做匀加速直线运动，目标3做变速曲线运动(小转弯机动)，三种运动方式基本上能够代表典型的运动方式，目标的运动规律如图3所示。假设初始时报告目标时间点一致，后续由于探测和数据链上时间的差距，假设N =3 有节点播报，播报的周期分别为1 s、2 s、3 s。

图3 目标运动模拟Fig.3 Simulation of target movement

3.2 实验结果分析

根据以上假设，可以确定本系统的设定周期为1 s，由于网络原因和误差的影响，每个时刻点播报都不可能是严格按照其周期进行播报，则需要对全部数据进行定周期外推。

为了说明本算法的有效性，本文对对准周期采用两种算法进行对比，采用最小二乘法曲线拟合和本文的定周期自适应卡尔曼滤波算法分别进行试验。由于数据播报不是严格的定周期，则通过取整获取理论周期。图4和图5是几种不同算法对准后的效果图。

图4 时间对准结果Fig.4 Simulation result of time－alignment

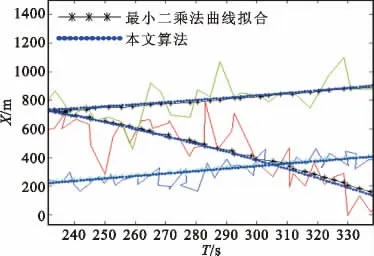
图5 局部放大图Fig.5 Partial enlargement of simulation result

从图4与图5中可以看出，对于不同的运动，其误差水平有所不同，对匀速直线运动而言，两种算法性能上结果差别比较小，对于本文算法，在匀加速直线运动和曲线运动中，最小二乘曲线拟合算法的误差明显比本文算法要差。通过实验可以看出，不同的时间对准都在一定程度上可以纠正其错误，本文的算法效果与其他算法相比有一定的提高。

4 结束语

本文通过建立固定周期时间对准策略，加入以报告质量为融合权重的自适应融合策略，为分布式数据链系统同一时刻对同一目标提供较为准确的观测值提供了解决方案。实验表明，本算法可以有效地完成时间对准操作，相对传统算法有一定提高。

由于本文未考虑实际战场环境中的敌方干扰和欺骗因素，因此仿真结果仅代表理想情况下的结果，下阶段的主要工作是开展复杂战场坏境下的数据链时间对准算法研究。

［1］ 何友，王国宏，关欣，等.信息融合理论及应用［M］.北京:电子工业出版社，2010:102－557.HE You，WANG Guohong，GUAN Xin，et al. Information fusion theory and application［M］. Beijing:Publishing House of Electronics Industry，2010:102－557.(in Chinese)

［2］ Llinas J，Waltz E. Multisensor Data Fusion［M］. Norwood，Massachusetts:Artech House，1990.

［3］ 赵宗贵.信息融合技术现状、概念与结构模型［J］. 中国电子科学研究院学报，2006，1(4):305－312.ZHAO Zonggui. Current Status，Concept and Structure Model of Information Fusion Technology［J］. Journal of China Academy of Electronics and Information Technology，2006，1(4):305－312.(in Chinese)

［4］ 韩崇昭. 信息融合理论与应用［J］. 中国基础科学，2000(7):14－18.HAN Chongzhao. Information fusion theory and application［J］.Chinese Basic Science，2000(7):14－18.(in Chinese)

［5］ 段同乐，赵华敏，薄涌.基于模糊相似度的地面目标跟踪算法研究［J］.无线电工程，2007，37(10):56－58.DUAN Tongle，ZHAO Huamin，BO Yong. Study on Algorithm for Ground Target Tracking Based on Fuzzy Similarity［J］.Radio Engineering of China，2007，37(10):56－58.(in Chinese)

［6］ Gao S S，Zhang J M，Zhou T.Large Numbers Law for Sample Mean of Random Weighting Estimate［J］.Information Sciences，2003(1):151－156.

［7］ Dela Cruz E J，Alouani A T，Rice T R，et al.On Multisensor Track Alignment［C］//Proceedings of the 31st IEEE Conference on Decision and Control. Tucson，AZ:IEEE，1992:3779－3800.