基于C-RAN 与LTE-Hi 的BR-OFDMA 导频图案设计*
2015-03-18徐宇明吕世起曾银强
余 翔,徐宇明,吕世起,曾银强
(重庆邮电大学,重庆400065)
1 引 言
近年来,由于移动通信的数据量迅速增长,尤其是在室内及热点场景,结合热点及室内覆盖的长期演进(Long Term Evolution Hotspot/Indoor,LTE-Hi)[1]被提出。而新一代集中式云构架无线接入网(Cloud Radio Access Network,C-RAN)[2]在热点地区有着十分明显的优势,因此两者的结合在未来将成为一种趋势。文献[1]提到,LTE-Hi 要提供大数据量流量,就必须工作在能提供大带宽的高频段3 GHz 以上,且小区结构也将变成高密度、小范围覆盖,这样就存在更高的小区边缘干扰。正交频分多址(Orthogonal Frequency Division Multiple,OFDM)技术由于其优良的性能也将成为未来移动通信的关键技术之一。在处理小区同频干扰的问题上,文献[3]提到应用OFDM 结合码分多址(Code Division Multiple Access,CDMA)的块重复的正交频分多址(Block Repeat Orthogonal Frequency Division Multiple Access,BR-OFDMA)技术、动态区间协调减少同频干扰。动态的小区间协调也是消除干扰的重要手段,其受网络架构、回程链路、信道估计[4]等外部因素的影响。由于C-RAN 本身的架构已经解决了前两个问题,所以信道估计就变得尤为重要。LTE-Hi 中提到其通信环境比较稳定,所以其信道质量变化较慢,传统的密集导频插入就会浪费频谱资源,所以LTE-Hi 中将使用较少的导频[1]。传统信道估计方法如最小均方误差(Minimum Mean Square Error,MMSE)法和最小二乘(Least Square,LS)法需要插入大量导频,不太适合在LTE-Hi 中应用。现今,稀疏信道估计已成为通信领域的一大研究热点[5-8]。随着压缩感知(Compressive Sensing,CS)技术的提出和逐渐成熟[9-10],其被广泛应用在OFDM及高速宽带系统信道的估计中。研究表明:基于压缩感知的稀疏多径信道估计无需通过插值手段重构数据子载波上的信道信息,就可以有效地降低信道估计误差,减少所需传输的导频数目,提高频谱利用率[7]。由此本文将应用C-RAN 架构承载LTE-Hi,并结合BR-OFDMA 和压缩感知技术,设计能满足LTE-Hi 的导频图案。
2 C-RAN 下的LTE-Hi 小区情况
C- RAN 由基带处理单元(Base Band Unit,BBU)和拉远天线(Remote Radio Head,RRH)组成,BBU 协调处理所有小区数据,通过光纤统一控制所有RRH,解决了传统小区间X2 接口通信能力不足的问题。为使问题清晰且不失一般性,在此分析三小区情况,如图1所示。

图1 小区情况Fig.1 Cell situation
图中红色表示三小区干扰情况,蓝色表示AB 双小区干扰情况,BC、AC 之间双小区干扰情况类似。由于LTE-Hi 用的高频载波产生更大的阴影衰落,所以导致小区范围减小,发射功率提高。但当小区边缘存在直射情况时,边缘干扰就会比传统小区严重得多,因此各小区的导频信息也会受到不同程度的干扰,所以在设计导频图案时要根据不同干扰情况设计不同的导频结构。此时,各小区之间的协作就需要大量信令交互,因此C-RAN 架构有着明显优势。
3 LTE-Hi 下的BR-OFDMA 及信道模型
3.1 BR-OFDMA 简介
BR-OFDMA 结合了CDMA 的思想,利用块重复和联合检测技术有效减少了小区间干扰。通过将多个重复码(Repeat Code,RC)分别与基本单元块中的数据相乘并重复调制,获得多个重复单元块。重复的调制次数为重复因子(Repeat Factor,RF),重复因子为6 时的信号结构如图2所示。当不同小区用户使用相同时频资源时,各用户使用不同RC 码加权,接收端就可根据不同RC 进行联合检测分离数据,进而降低小区间干扰。
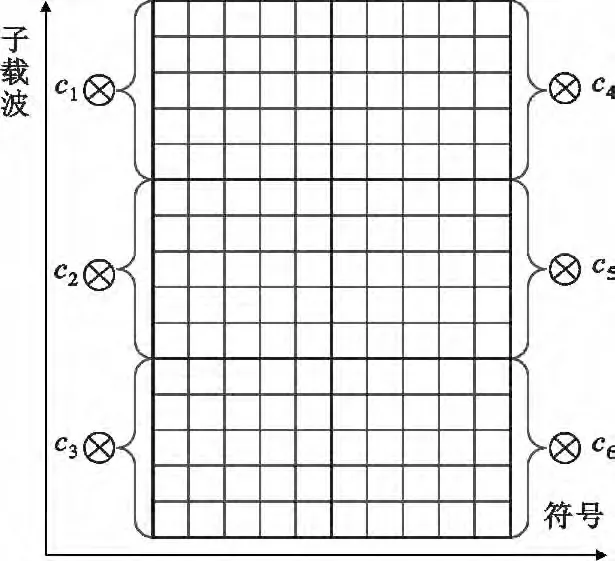
图2 BR-OFDMA 信号结构Fig.2 BR-OFDMA signal structure
3.2 LTE-Hi 下的动态BR-OFDMA
BR-OFDMA 的特点之一是可根据干扰情况动态调整重复因子,进而达到性能和资源消耗上的平衡。如第2 节中的情况,处于3 个小区干扰下的用户可根据干扰大小的不同动态调整RF 为4~6;当检测到用户处于两小区干扰时,又可将RF 调整为2~4;当用户在小区中心附近没有干扰时,RF 可变为1,此时的BR-OFDMA 就变为了传统的OFDMA。在C-RAN 环境下,所有数据都在BBU 中统一调度,各小区可完全可同步动态协调。
3.3 LTE-Hi 信道特点
热点地区的用户基本属于静止或低速移动的,多普勒效应极低,信道情况变化较慢,收发端距离较近,小区间的干扰因远远超过噪声,故成为主要考虑的干扰方式。并且LTE-Hi 为提高频谱效率提出两点要求,一是高阶的正交幅度调制(Quadrature Amplitude Modulation,QAM)如256QAM,二是更稀疏的导频密度。
在传统信道估计中,最大多普勒频移fmax和最大多径时延τmax两个参数影响着导频密度。根据二维奈奎斯特采样定理,时域导频间隔Nt和频域导频间隔Nf应该满足
式中,T 表示OFDM 符号的时间长度,Δf 表示子载波带宽。现有LTE 标准中定义需要插入的导频较多[11],浪费的资源也较多。考虑到LTE-Hi 的特性与需求,可分别从频域和时域减少导频密度,频域方面引入压缩感知技术减少导频插入数量;时域方面,由于LTE- Hi 下多普勒效应不明显,信道变化缓慢,可根据公式(1)设计成动态调整插入间隔,未插入导频的符号采用插值估计。
3.4 压缩感知信道估计数学模型
设h(n)为离散的时域信道冲激响应,L 为离散时间信道模型中抽头延时的总个数,也就是信道最大长度,其数学模型为

对于稀疏信道,向量h =[h0,h1,…hL-1]T只有很少的非零值,大部分接近于零。设OFDM 子载波数目为N,发送信息序列为x(n),零均值高斯加性白噪声为z(n),接收端收到的时域信号为y,则频域表示为
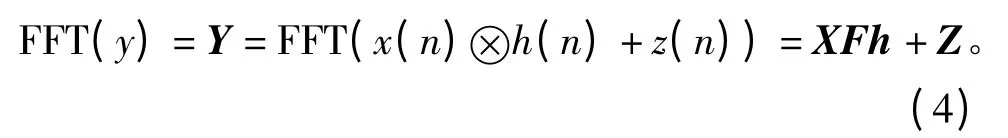
F 为从N×N 维傅里叶矩阵中选择的前L 列构成的部分随机傅里叶矩阵:
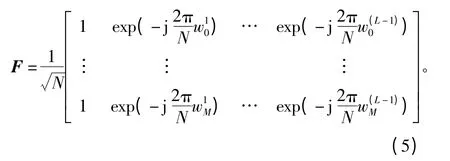
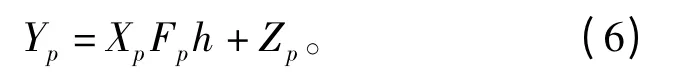
其部分随机傅里叶矩阵变为P×L 维矩阵,系数为

由此可知,从式(6)中估计h 是一个典型的稀疏信号重建问题,它完全可以采用基于压缩感知的重建算法完成。本文重点关注导频图案的设计。
4 LTE-Hi 的BR-OFDMA 导频图案设计
4.1 多小区频分复用导频结构
为了减少各小区导频间的干扰,导频需经过复用来提高信道估计的准确性,所以本文设计利用频分复用来区分不同小区导频。如前文所述,可能存在无干扰、双邻区干扰和三邻区干扰三种情况,只有在无干扰情况下才无需复用。下面就三种情况给出图示,设在一个符号的不同子载波中用P 表示导频,D 表示数据,“空”表示什么也不发。
图3表示无干扰情况下,各小区可独立发送信息。图4表示终端会收到同时来自A、B 两小区的信号,为减小干扰,当A 小区发导频时B 小区在同一时频资源不发任何数据,当B 小区发导频时A 小区在同一时频资源也不发任何数据,而C 小区对其无干扰,所以C 可独立发送数据。图5表示终端能同时收到3 个小区的信号,同理,当其中一小区发导频时,其他两小区在同一时频资源保持沉默。

图3 小区间无干扰导频复用图Fig.3 No inter-cell interference pilot multiplexing

图4 双邻区干扰导频复用图Fig.4 Dual neighboring interference pilot multiplexing

图5 三邻区干扰导频复用图Fig.5 Three neighboring interference pilot multiplexing
4.2 干扰探测导频
由于干扰小区数量与干扰强度影响着重复因子和导频结构,所以需要插入干扰探测导频来确定终端受到干扰的小区数量与干扰强度。由于LTE-Hi下终端变化较慢,所以干扰探测导频插入数量无需太多。本文设计在每个重复资源块组最后一个符号中间频段的3 个连续子载波上,以频分方式使三小区干扰探测导频复用,如图6所示。

图6 干扰探测导频复用图Fig.6 Interference detection pilot multiplexing
从图6可看出各小区导频无干扰,终端可根据相应位置接收到的导频强度判断来自各小区的干扰强度,然后反馈给各小区,为下一个资源块的设计提供参数。
4.3 重复因子的确定方法
重复因子是BR-OFDMA 的核心参数之一,关系到通信质量和系统效率的平衡。干扰的存在会导致误码,由此产生的误块会触发系统启动自动重传机制,这就会消耗物理资源和造成延迟。当误块率太高时,就会对通信质量造成严重影响,这时就需要提高重复因子来降低干扰,但当重复因子太多时又会消耗过多时频资源,降低频谱利用率。所以本文利用干扰强度大小来确定重复因子的值,采用分段式的设计方案。干扰强度定义为信干比(Signal to Interference Ratio,SIR):
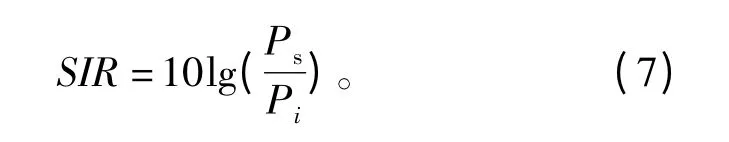
分段式设计方案是根据干扰强度不同而调整重复因子,在通信质量与资源利用率之间进行平衡,所以分段方式与实际环境和应用需求有密切关系。为了说明该方案的设计思路,本文给出一种在仿真环境下的设计实例。为了得到信干比在不同重复因子下的误码率,本文用Matlab 作为仿真环境。仿真中采用LTE-Hi 提出的256QAM 高阶调制,由于LTE-Hi 尚未规定信道编码标准,所以本文采用LTE 标准中定义的Turbo 码作为信道编码,用适合高速运算的改进型最大后验概率(Maximum A Posteriori,MAP)译码算法Max-log-MAP 进行仿真分析。
图7是双邻区干扰下不同重复因子的误码率情况。从图中可见,由于256QAM 的抗干扰能力很弱,当不采用重复因子时,5 dB 以下无法正常译码,5~30 dB 时的通信质量也很差,所以只有在小区中心干扰很低的情况下才不需要重复因子。虽然重复因子为3 时的增益比重复因子为2 时大,但消耗时频资源也较多。而只有在5 dB 以下时,重复因子为4才会比重复因子为3 时有明显优势。
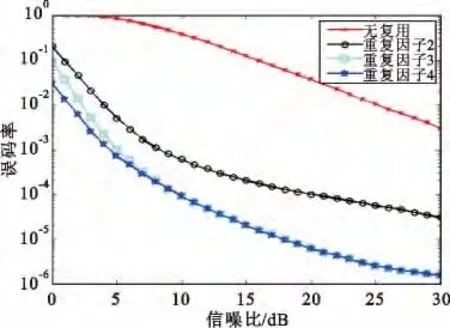
图7 双邻区误码率仿真Fig.7 Dual neighborhood BER simulation
根据以上分析,本实例在双邻区干扰时重复因子设计为

此种选择是为了保证通信质量的前提下又不会太浪费时频资源。图8是三邻区干扰下不同重复因子的误码率情况。

图8 三邻区误码率仿真Fig.8 Three neighborhood BER simulation
同理,本实例在三邻区干扰时重复因子设计如下:

在实际应用中,由于环境、硬件、时频资源、误码率需求等不尽相同,误码曲线也不同,所以该方案的自适应性就可动态调整重复因子的分段方式以满足不同需求。
4.4 导频的频域插入
当重复因子确定后,就确定了重复块组结构,从而得知重复块组的子载波数。根据压缩感知信道估计理论,频域插入导频的数量是信道稀疏度的4~8倍,所以本文根据前一个重复块组信道估计得到的稀疏度来确定下一个重复块组需要插入的导频数量。当存在小区间干扰时,就要进行小区间协作,应用分布式压缩感知理论,以频分复用方式联合设计导频插入图案,由4.1 节可知,由于空数据的存在,此时占用的子载波数为所有参与小区导频数之和。压缩感知的导频插入位置需要很高的随机性,为了让收发双方同时可知导频位置,小区与终端需采用同一个随机因子下的伪随机算法生成导频位置,且参与小区不能有重叠,下面举例说明。假如检测到终端处于双邻区情况,假设重复块组子载波数为10个,编号为1~10,设A 小区需要插入2 个导频,伪随机算法生成的插入子载波编号为2、8,设B 小区需要插入3 个导频,伪随机算法生成的插入子载波编号为1、6、9,则插入导频如图9示例,其中Pa是A小区的导频,Pb是B 小区的导频。
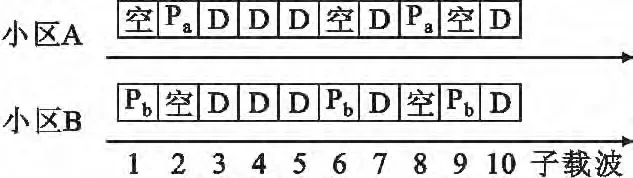
图9 频域插入示例图Fig.9 Frequency domain insert
4.5 导频的时域间隔
由于LTE-Hi 下主要存在静止或极低速用户,所以LTE-Hi 规定其导频在时域的间隔要比LTE大,这样可以节省频谱资源。如果采用动态自适应间隔,可以更有效地分配资源,但会增加信令开销。根据3.3 节分析可知导频的时域间隔受到最大多普勒频移的影响,假设载波频率为3.5 GHz,用户最大移动速度不大于30 km/h,此时检测到的最大多普勒频移为97.22 Hz,如果采用普通循环前缀(Cyclic Prefix,CP),根据公式(1)可以算出最大插入间隔为36 个符号,也就是在一帧中至少有4 个符号需要插入导频。当移动速度减少为10 km/h 时,最大多普勒频移变为32.4 Hz,同理算出最大插入间隔为108个符号,这时一帧中只需在至少一个符号中插入导频。这样的方式既可以节约时频资源,又可以在使用相同算法和准确的同步就能使双方同时知道导频位置,而不增加信令开销的条件下,将信道信息和多普勒频移数从终端反馈到基站。
4.6 导频序列的选择
Zadoff-chu(ZC)序列为非二进制单位幅度序列,满足恒幅零自相关(Const Amplitude Zero Auto-Corelation,CAZAC)特性,能够在频域上保持恒幅,有利于进行无偏的信道估计,在时域上能够保证低的立方量度,有利于在小区边缘进行发送功率的提升。其良好的自相关特性有利于进行精确的信道估计,不同训练序列之间良好的互相关特性有利于降低小区间干扰。因此,LTE 中采用了这种序列,本文也采用此种序列作为测试用的训练序列。长度为P的训练序列的生成公式如下:式中,q 为与P 互质的整数。
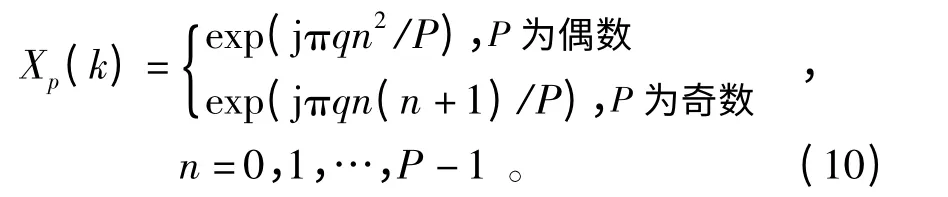
4.2 节中已经提到,对于上一个OFDM 符号估计出的信道稀疏度K,要插入P=6K 个导频。
4.7 总体过程
由以上分析总结出整个过程如图10所示。

图10 总体过程图Fig.10 Overall flow diagram
图中总体过程,首先根据3.3 节分析确定导频在时域符号的插入间隔,保证既能恢复信道信息又不浪费时域资源;然后利用第4 节的方法确定BR-OFDMA 分块参数;最后将导频序列插入相应的位置。
5 仿真分析
为了验证本文方案的可行性,针对双邻区与三邻区干扰两种情况,用Matlab 对误码率进行仿真分析。双邻区干扰仿真参数如下,信噪比范围设为0~30 dB,仍然采用LTE 中的Turbo 码作为信道编码,运用4.3 节的自适应分块原则,重复块子载波数为256,信道长度64,A、B 小区信道稀疏度分别为5、7,用普通CP,假设满足无码间干扰,插入导频数分别为20、28,为了减少其他因素的影响,所以不用自适应编码调制,而是固定用256QAM 调制。由于同步正交匹配追踪算法(Synchronous Orthogonal Matching Pursuit,SOMP)在分布式压缩感知信道估计中表现出较好性能,所以本文采用此算法作为恢复测试算法。
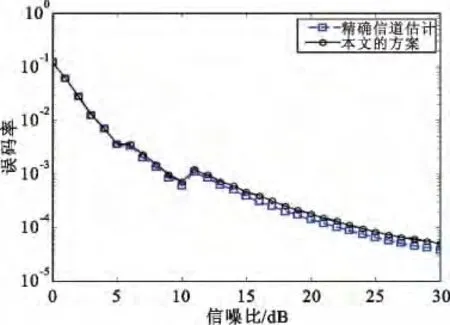
图11 双邻区信道估计误码率对比图Fig.11 Dual neighborhood channel estimation BER comparison
因采用自适应分块处理,所以图中的误码率并不是随着信干比增加而降低。当信干比为6 dB时,重复因子由4 降到3,频带利用率增加,但抗干扰性降低;当信干比为11 dB时,重复因子由3 降到2,频带利用率进一步提高,但抗干扰性明显减弱,误码率提高,但仍能保持在10-3以下,此处体现了频带利用率与误码率之间的折衷设计,实际中可根据需求改变分段情况。由于本文的导频方案能够消除大部分干扰,所以本文信道估计方案下的误码率与理想信道估计性能十分相近。图中的精确信道估计就是在完全知道信道信息情况下的误码率。由于在低信干比时,干扰对误码率的影响远远超过了信道估计误差的影响,所以在低信干比时误码率差别不大,高信干比时,信道估计误差会明显影响误码率。三邻区干扰仿真时,设A、B、C 小区信道稀疏度分别为5、6、7,插入导频数分别为20、24、28,其他参数保持不变,得到误码率如图12所示。

图12 三邻区信道估计误码率对比图Fig.12 Three neighborhood channel estimation BER comparison
从图中可见,在6 dB 和11 dB 处将重复因子调整为4 和3,误码率也出现了转折。在三邻区干扰环境下,本文的方案同样有较好性能,由于使用了较高的重复因子,所以其性能优于双邻区干扰环境。
6 结 语
本文将C-RAN 与LTE-Hi 结合,并根据其小区边界的特点,应用BR-OFDMA 和压缩感知信道估计技术,提出一种新的导频图案设计方案。该方案不仅能满足LTE-Hi 需要减少导频数量的要求,还能在LTE-Hi 的高强度边界干扰的环境下表现较好性能。同时,该方案能在C-RAN 平台下灵活完成多小区间的协作配置与同步,能自动根据干扰情况,在资源消耗与性能之间进行平衡。仿真表明该方案即使在低信干比环境下仍能将误码率控制在10-3以下。
本文所提出的方案需要多小区协调,信令方面会变得更复杂;由于压缩感知信道估计计算量较大,对硬件的需求也会增加;以上问题将会影响本方案在实际中的应用,这些都是下一步的研究方向。
[1] Chen Shanzhi,Wang Yingmin,Qin Fei,et al. LTE-Hi:A new solution to future wireless mobile broadband challenges and requirements[J]. IEEE Wireless Communications,2014,6(14):1536-1284.
[2] China Mobile Research Institute.C-RAN:The Road Towards Green RAN[M]. Beijing:China Mobile Research Institute,2011.
[3] Chen Shanzhi,Wang Yingmin,Ma Weiguo,et al. Technical innovations promoting standard evolution:from TD-SCDMA to TD- LTE and beyond[J]. IEEE Wireless Communications,2012,2(12):1536-1284.
[4] Kevork M. Performance evaluation of QoS aware scheduling algorithm in C-RAN CoMP for DL LTE-A[D].Bremen:University of Bremen,2014.
[5] Wu C J,Lin D W. Sparse channel estimation for OFDM transmission based on representative subspace fitting[C]∥Proceedings of 2005 IEEE 61st Vehicle Technology Conference. Piscataway:IEEE,2005:495-499.
[6] Raghavendra M R,Giridhar K. Improving channel estimation in OFDM systems for sparse multipath channels[J].IEEE Signal Processing Letters,2005,12(1):52-55.
[7] Taubock G,Hlawatsch F,Eiwen D,et al. Compressive estimation of doubly selective channels in multicarrier systems:leakage effects and sparsity-enhancing processing[J]. IEEE Journal of Selected Topics in Signal Processing,2010,4(2):255-271.
[8] Berger C R,Zhou S,Chen W,et al. Sparse channel estimation for OFDM:Over-complete dictionaries and super-resolution[C]∥Proceedings of 2009 IEEE Workshop on Signal Processing Advances in Wireless Communications. Perugia,Italy:IEEE,2009:196-200.
[9] Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory,2006,52(4):1289-1306.
[10] Baraniuk R G. Compressive sensing[J]. IEEE Signal Processing Magazine,2007,24(4):118-120,124.
[11] 3GPP. TS 36.211 v11.4.0,Evolved Universal Terrestrial Radio Access(E- UTRA);Physical channels and modulation(Release 11)[S].
