基于回波数据压缩的MIMO－SAR 成像方法*

谢矿生

(武警工程大学 装备工程学院，西安710086)

1 引 言

多发多收合成孔径雷达(Multiple Input Multiple Output Synthetic Aperture Radar，MIMO－SAR)采用空间并行采样技术能够提供丰富的空间自由度，从而可有效解决传统单通道SAR 成像过程中方位向高分辨与大测绘带之间的矛盾问题，具有十分广阔的发展与应用前景［1－4］。然而，由于机载平台的资源和硬件处理能力有限，无法完成较为复杂和精确的成像处理，只能对雷达回波数据进行一些简单的预处理，然后传输给地面接收端或者预警机进行更为复杂的运算和数据分析处理。考虑到MIMO－SAR 成像系统多通道的特点，其回波数据量在同等条件下是单通道SAR成像系统的数倍，这对数据传输信道和实时传输提出了严峻的挑战。因此，如何减少MIMO－SAR 成像系统的回波数据量是值得研究的问题。

近年来，由美国科学家Donoho 提出的压缩感知(Compressed Sensing，CS)理论为解决上述问题提供了较为有效的途径与方法［5］。该理论指出，如果信号具有稀疏性，那么可以从严重降采样的数据中实现该信号的高概率重构。可以说，CS 理论利用了信息采样取代了信号采样，这样采样速率由信息在信号中的结构和内容决定，而不是信号的带宽。基于该特性，国内外的研究人员已经将CS 理论应用于雷达数据的压缩与成像中［6－9］。文献［6－7］利用CS 理论对二维傅里叶处理之后的SAR 数据进行一维的解编码，从而减少了SAR 系统的传输数据量。文献［8］提出了稀疏孔径SAR 成像方法，利用稀疏孔径降低了回波数据量。目前的研究成果大多都集中于单站点雷达的数据压缩处理，而对于多站点MIMO 雷达的数据处理应用还比较少。本文将压缩感知理论引入到MIMO－SAR 的数据压缩处理中，提出了在MIMO 雷达载机传输端利用压缩感知理论将预处理后的回波数据压缩并传输，然后在地面接收端利用CS 重构算法直接重构得到距离多普勒域数据，进而进行方位向成像处理的方法，这样可大幅减少MIMO－SAR 传输的数据量，从而有效提高回波数据的传输效率。

2 MIMO－SAR 回波数据分析

假设天线阵元沿着载机的航线方向排列，一共包含P 个天线阵元，分别记为X1，X2，…，XP。载机的飞行速度为v，其高度为H，设定观测场景具有N个散射点，其中第Pn个散射点的位置坐标为(xn，yn，zn)，n =1，2，…，N。该散射点到航线的垂直距离为Rn。MIMO－SAR 成像的几何构型图如图1所示。

图1 MIMO－SAR 成像几何构型图Fig.1 MIMO－ SAR imaging geometry figure

考虑到MIMO 雷达的回波信号需要进行分集处理，因此发射的信号应该具有正交性。本文采用正交频分线性调频(Orthogonal Frequency Division Linear Frequency Modulation，OFD－LFM)［10］信号作为MIMO－SAR 系统的发射信号，那么第p 个天线阵元发射的信号为

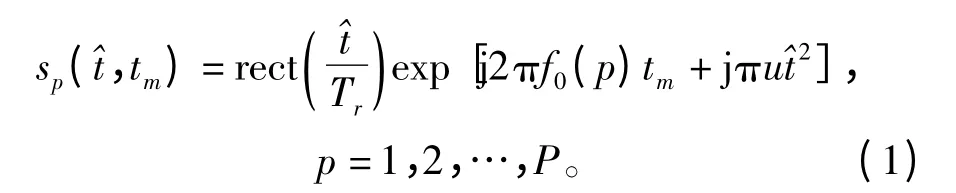
式中，rect(t)是矩形窗函数，当－1/2≤t≤1/2 时，其值为1;u 为信号的调频率;Tr为发射脉冲宽度;t为快时间;tm为慢时间，并且中心频率为

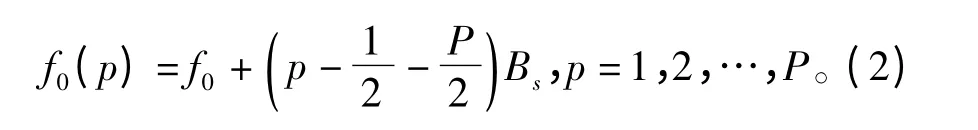
式中，f0为发射信号的初始载频，Bs为两个相邻阵元发射信号的步进带宽。那么第q 个接收天线收到所有发射天线的信号表达式为

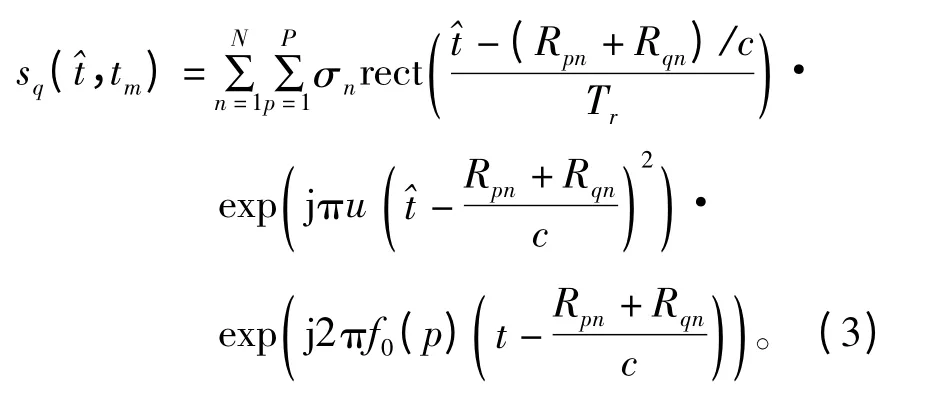
式中，σn表示目标的后向反射系数，c 为光速，Rpn为第p 个发射阵元到第n 个点目标的距离，Rqn为第n个点目标到第q 个接收阵元的距离。对回波信号sq(，tm)进行去载频处理，并进行分离处理，得到来自第p 个发射天线的回波基频信号为

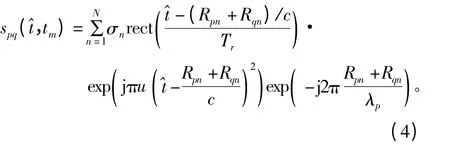
式中，λp=c/f0(p)。考虑到MIMO－SAR 系统收发分置的特点，在进行成像处理之前需要先补偿由收发分置阵元转换为收发同置阵元而导致的相位误差［11］。文献［12］针对这一问题，给出了较为详细的分析，因此公式(4)经过相位误差补偿后，可重新写为

式中，Rpqn为等效相位中心Xpq到目标点Pn(xn，yn，zn)的距离。其次对式(5)做距离向和方位向傅里叶变换，得回波信号的二维频域表达式为

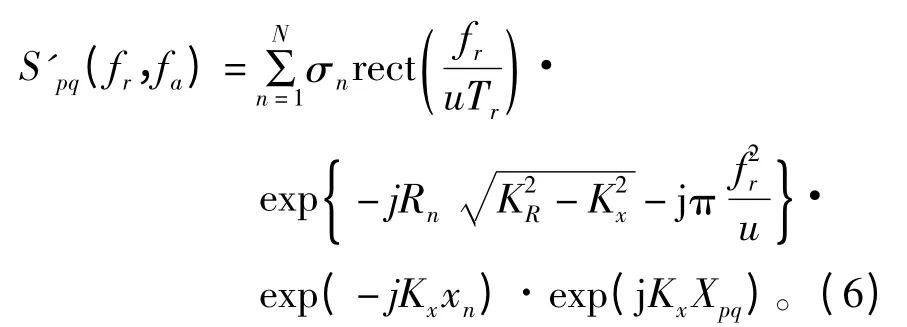
式中，KR=4π(f0(p)+fr)/c ，Kx=2πfa/v。

3 基于数据压缩的成像方法

3.1 回波数据预处理及稀疏性分析

为便于数据补偿，按照文献［13］和距离徙动算法(Range Migration Algorithm，RMA)，考虑到实际运动误差补偿的需要，按照文献［13］的方法首先将式(6)第一个指数项按照参考距离R0分为不依赖距离和依赖距离两部分，即

那么，构造的一致压缩的参考函数为

将式(6)与式(9)相乘完成一致压缩处理，这样参考距离R0处的数据完全聚焦，而其他距离处的目标有残余的相位φd(fr，fa，Rn－R0)。由于式(6)中的残余相位是fr的非线性函数，若直接对信号做距离向快速傅里叶逆变换(Inverse Fast Fourier Transform，IFFT)，当 (Rn－R0)≠0 时，目标就会出现散焦现象。对式(6)做插值处理，通过尺度变换操作将式(6)的根式替换为4π(f0(p)+fb)/c，即

这样通过Stolt 插值的补余聚焦，实现了剩余距离徙动的校正和残余相位的补偿，可记为S*(fr，fa)。在实际的数字信号处理中，可看作一个二维矩阵，大小为L×N，其中L 为多普勒单元数，N 为距离单元数。将矩阵的第l(l=1，2，…，L)行记为那么经过距离向的离散傅里叶逆变换(Inverse Discrete Fourier Transform，IDFT)处理，可得观测场景的一维距离像，其公式表示为

式中，矩阵Ψ 为DFT 变换矩阵，具体可写为

当观测场景满足稀疏性要求时，其一维距离像的峰值数相对于整个距离向上的采样点数是很少的，因此在距离向上满足稀疏性要求，这样MIMO－SAR 的回波数据经过预处理后能够得到其稀疏化表征。

3.2 基于数据压缩的成像方法

为了实现对预处理数据的压缩，在CS 理论中即为通过构造低维观测矩阵实现对数据的降维处理。构造的广义单位阵为降维矩阵，从而实现对预处理数据S*(fr，fl)的压缩，降维观测矩阵记为ΦM×N，其中中的任意行向量除了第mc个元素为1 外，其余元素均为0，mc随机选取。这样即可得到压缩后的数据其公式表示为

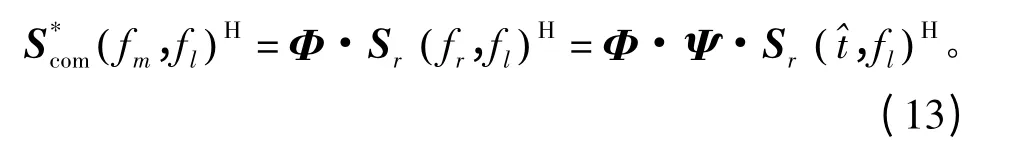
考虑传输噪声的影响，式(13)可重新写为

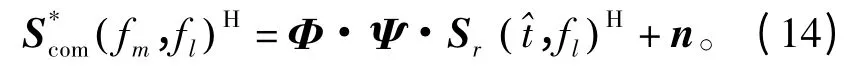
对所有的l =1，2，…，L 均进行上述压缩处理，即可得到压缩后的预处理的MIMO－ SAR 数据这样MIMO 雷达载机的信号传输端只需要即可，该数据的大小为L×M，相比于原始数据S*(fr，fa)压缩了L×(N－M)，压缩比定义为η =(N－M)/N，其中，N 为原始数据量，M为压缩后剩余的数据量。在接收端，根据CS 理论，利用求解下述表达式即可得到

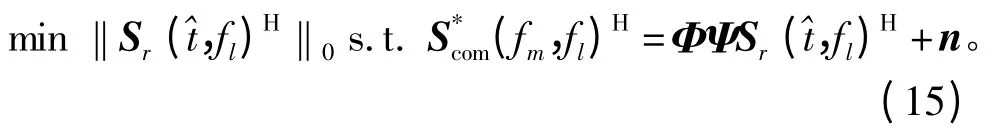
对所有的l =1，2，…，L 均进行式(15)的求解，即可得到观测场景的距离多普勒域数据Sr(，fa)，再对其进行方位向的IDFT 处理，即可得到观测场景的成像结果。

4 仿真实验

以3 发3 收的MIMO 雷达阵列为例，对MIMO－SAR 系统的回波数据压缩成像过程进行仿真验证。MIMO－SAR 系统正侧视模式工作，其与观测场景的几何位置关系如图1所示。3 个天线阵元的位置分别为0 m、0.5 m、1 m，其余的仿真参数如表1所示。

表1 雷达系统参数Table 1 Radar system parameters

首先以单散射点目标为例进行验证，点目标的坐标(x0，y0，z0)=(0 m，4150 m，0 m)。得到的点目标成像结果如图2所示，其中(a)和(b)分别是MIMO－SAR 全数据的成像结果与其峰值旁瓣示意图，(c)和(d)分别是回波数据压缩比η =0.75 时利用本文提出的方法得到的成像结果。对比可以看出，图2(d)的旁瓣明显低于全数据得到的结果，说明了利用本文方法得到的结果具有较好的聚焦性能，从而也说明了利用本文方法能够在大幅压缩回波的条件下获得较好的成像结果，验证了所提方法的有效性。

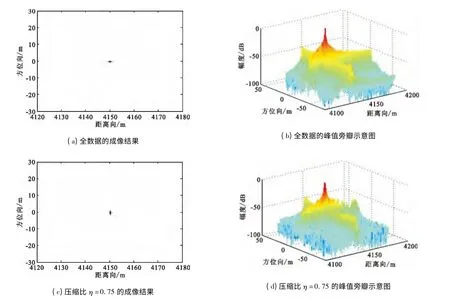
图2 MIMO－SAR 单点目标成像结果Fig.2 The results of MIMO－SAR point target imaging

为了更能说明本文方法的有效性，下面采用海面场景的面目标进行仿真验证。MIMO 雷达的参数设置如上所述，仍然为3 发3 收。图3给出了在全数据和压缩数据条件下的成像结果，其中(a)是在全数据条件下得到的成像效果，(b)是在压缩比η =0.75 条件下利用本文基于CS 的方法得到的结果，可以看出得到了较为理想的成像结果，便于后续的目标识别处理，从而再次验证了本文方法的有效性。

图3 MIMO－SAR 面目标成像结果Fig.3 The results of MIMO－SAR surface target imaging

5 结束语

本文针对MIMO－SAR 回波数据量较大问题进行研究，提出了回波数据压缩的MIMO－SAR 成像方法。在详细分析MIMO－SAR 回波信号模型的基础上，给出了基于RMA 算法对MIMO－SAR 回波信号的预处理方法并进行了稀疏性分析，然后利用压缩感知降维思想对预处理的数据进行了压缩采样并传输，在地面接收端利用CS 重构理论进行重构处理并最终成像。最后利用海面场景的仿真实验验证了本文方法在大幅压缩回波数据的基础上能够实现MIMO－SAR 的准确成像。

［1］ 武其松，井伟，邢孟道，等. MIMO－SAR 大测绘带成像［J］. 电子与信息学报，2009，31(4):771－775.WU Qisong，JING Wei，XING Mengdao，et al. Wide swath imaging with MIMO－SAR［J］. Journal of Electronics ＆Information Technology，2009，31 (4):771－ 775.(in Chinese)

［2］ Ender J H G，Klare J. System architectures and algorithms for radar imaging by MIMO－SAR［C］//Proceedings of 2009 IEEE Radar Conference. Pasadena，CA:IEEE，2009:1－6.

［3］ 黄平平，邓云凯，徐伟，等. 基于频域合成方法的多发多收SAR 技术研究［J］. 电子与信息学报，2011，33(2):401－406.HUANG Pingping，DENG Yunkai，XU Wei，et al. The research of multiple input and multiple output SAR based on frequency synthetic［J］. Journal of Electronics ＆ Information Technology，2011，33 (2):401－ 406.(in Chinese)

［4］ Gebert N，Krieger G. Azimuth phase center adaptation on transmit for high－ resolution wide－ swath SAR imaging［J］. IEEE Geoscience and Remote Sensing Letters，2009，6(4):782－786.

［5］ Donoho D L. Compressed Sensing［J］. IEEE Transactions on Information Theory，2006，52(4):1289－1306.

［6］ Bhattacharya S，Blumensath T，Mulgrew B，et al. Fast encoding of synthetic aperture radar raw data using compressed sensing［C］//Proceedings of 2007 IEEE Workshop on Statistical Signal Processing. Madison，USA:IEEE，2007:448－452.

［7］ Wang Min. Raw SAR data Compression by Structurally Random Matrixbased Compressive Sampling［C］// Proceedings of 2009 2nd Asian－Pacific Conference on Synthetic Aperture Radar.Xi'an:IEEE，2009:1119－1122.

［8］ Herman M A，Strohmer T. High－ resolution radar via compressed sensing［J］. IEEE Transaction on Signal Processing，2009，57(6):2275－2284.

［9］ Gu Fufei，Chi Long，Zhang Qun，et al. Single snapshot imaging for MIMO radar with sparse antenna array［J］.IET Proceedings－ Radar，Sonar ＆ Navigation，2013，7(5):535－543.

［10］ 刘波，韩春林，苗江宏. MIMO 雷达正交频分LFM 信号设计及性能分析［J］. 电子科技大学学报，2009，38(1):28－31.LIU Bo，HAN Chunlin，MIAO Jianghong. OFD－ LFM signal design and performance analysis for MIMO radar［J］. Journal of University of Electronic Science and Technology of China，2009，38(1):28－31.(in Chinese)

［11］ Bellettini A，Pinto M A.Theoretical Accuracy ofsynthetic aperture sonar micro－ navigation using a displaced Phase center antenna［J］. IEEE Journal of Oceanic Engineering，2002，27(4):780－789.

［12］ 王力宝，许稼，皇甫堪，等. MIMO－SAR 等效相位中心误差分析与补偿［J］. 电子学报，2009，37(12):2688－2693.WANG Libao，XU Jia，HUANGFU Kan，et al. Analysis and compensation of equivalent phase center error in MIMO－SAR［J］. Chinese Journal of Electronics，2009，37(12):2688－2693.(in Chinese)

［13］ 彭发祥，李宏伟，蔡斌，等. 基于运动补偿的机载MIMO－SAR 高分辨成像算法［J］. 空军工程大学学报(自然科学版)，2012，13(1):73－78.PENG Faxiang，LI Hongwei，CAI Bin，et al. An imaging method of high resolution airborne MIMO－ SAR based on motion compensation［J］. Journal of Air Force Engineering University:Natural Science Edition，2012，13(1):73－78.(in Chinese)