传动轴动态当量夹角在商用车重载爬坡中的研究

文_孟凡生

传动轴动态当量夹角在商用车重载爬坡中的研究

文_孟凡生

在商用车传动轴系统布置设计时，传动轴当量夹角、最大夹角及角加速度幅值应严格限制并尽可能小，但在某些工况下，校核好的参数并不能避免商用车重载爬坡工况下动态当量夹角对整车异常振动造成的影响，这就需要使重载爬坡工况下的传动轴动态当量夹角满足设计要求。

1 故障描述

2014年5月，在河北唐山某品牌重卡服务站，批量出现某品牌6×4自卸车重载爬大坡抖动故障；但该车型在平整路面运行，无论空载还是满载，均没有出现抖动。如果对该车型传动轴采取二合一的改进方案，即可消除重载爬坡抖动故障。针对这一改进，笔者进行了深入分析，相关研究如下。

1.1 车辆基本情况

某品牌6×4(基本配置见表1)主要是为煤矿、铁矿、城建工程等用途开发的1款矿用工程型自卸车，运载货物主要有煤炭、铁矿石、渣土等；车辆工况恶劣，上、下坡路较多。

1.2 现场故障调研

经调查，该车型主要在矿区使用，路况恶劣，大部分是15～20°的斜坡，且车辆超载严重，图1～4为实地调研图片。

2 故障原因分析

2.1 商用车万向节传动运动分析(理论基础)

2.1.1 单万向节传动

图5为单万向节传动轴力学模型，普通十字轴式万向节的主动轴与从动轴转角间的关系为[1-1]：

其中，φ1是轴1的转角，为万向节所在平面与万向节连接的两轴所在的平面的夹角；φ2是轴2的转角；α是万向节连接的两轴之间的夹角，商用车中规定万向节传动输出轴与输入轴的夹角不大于7°。

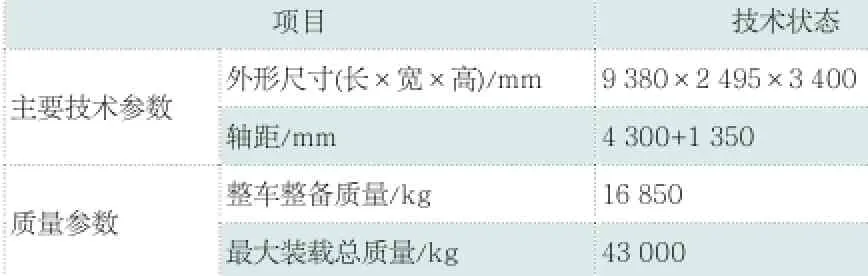
表1 某品牌6×4自卸车主要配置和技术参数

由公式(2-1-1)可见，就单十字轴而言，十字轴万向节输出轴与输入轴的存在转角差△φ，在万向节夹角α≤30°的条件下可用如下简化公式计算[1-1]：

设万向节主、从动轴的角速度分别为ω1和ω2，主、从动轴的角加速度幅值分别为ε1和ε2，则有[1-1]：

主传动轴转矩T1、从主传动轴转矩T2与万向节主、从动轴的角速度分别为ω1和ω2存在如下关系[1-2]：

具有夹角为α的十字轴万向节，仅在输入轴驱动转矩和输出轴发扭矩的作用下是不能平衡的，因为这两个转矩作用在不同的平面内，其向量互成一角度而不能自行封闭，根据万向节的力偶矩平衡可推断出，万向节还受有附加弯矩(二阶弯矩)。

当主动叉位置φ1=0°，附加弯矩来自于输出轴的反扭矩T2，可推导出附加弯矩：

当主动叉位置φ1=90°时，附加弯矩来自于输入轴的扭矩T1，可推导出附加弯矩：

万向节附加弯矩表达见图6、7。

附加弯矩变化周期是180°，在0与上两式表示的最大值之间变化；附加弯矩可激起与万向节相连机件的弯曲振动。

2.1.2 多万向节传动

多万向节传动的运动分析是建立在单万向节运动分析的基础上的，多万向节传动的转角差的计算公式与单万向节的相似，可以写成[1-1]：

通过上式可看出，多万向节传动输出轴与输入轴的运动关系，犹如具有夹角αe而主动叉具有初位相σ的单万向节传动一样。此夹角αe为多万向节传动的当量夹角。

假如多万向节传动的各轴轴线均在同一平面，且各传动轴两端万向节叉平面之间的夹角为零或90°，当量夹角为[1-1]：

式中正负号这样确定：当第一万向节的主动叉位于各轴轴线所在的平面内，在其余的万向节中，如果其主动叉平面与此平面重合定为正，与此平面垂直定为负，见图8。

图8中(a)的α1取“+”号，由于α2、α3主动叉所在平面与α1主动叉所在的平面垂直，取“-”号；同理图8(b)中α1取“+”号，α2取“+”号，α3取“-”号

当多万向节传动输入轴的角速度不变时，第i个万向节输出轴的角加速度幅值为[1-1]：

式中，αei为从第1个到第i个万向节传动的当量夹角。对于商用车，万向节传动输出轴的角加速度αe2ω12幅值不大于600 rad／s2[1-1]。

2.2 某品牌6×4自卸车重载爬坡抖动原因分析

2.2.1 水平工况下原传动轴状态分析

该车型动力线定位点为缸体后端面，坐标为X、Y、Z分别是(400，0，-323.8)，动力线夹角为2.83°，中桥主减倾角为2.9°，传动轴采用两根传动轴布置，传动轴长度第1节为1 030 mm，第2节为1 130～1 240 mm。平地空、满载传动轴夹角校核见图9。

传动轴各夹角及根据相关公式，相关结论校核结果见表2。

由表2可见，该车型传动轴原布置方案在水平工况下是符合行业标准要求。

2.2.2 水平工况载荷分析

车辆质心计算：根据该车辆整备质量16 850 kg，装载总质量为43 000 kg(货厢大小为6 500 mm×1 100 mm×2 300 mm，容积为16.5 m3，土石方密度按2.6 g/ cm3计算)。车辆质心参数见图10。

为了简化计算，采用平衡轴式后双联驱动桥支点可简化为一个单后桥支点，采用水平平稳运行状态。建立如图11所示受力模型，中后桥受力取平衡轴的中心。

根据受力平衡，对前轴取转矩，根据转矩平衡，所以：

F2X4975=G1X(4975-1850)+G2X(4975-562)

其中F2为后轴轴荷，可求出F2=48 726.7 kg。

2.2.3 、爬坡工况载荷分析

由于受到车辆质心高度的影响，在上坡的时候车辆的轴荷会向后桥转移，为了计算简单，选取平稳上坡或者停驻状态(坡度30%)。

建立图12所示受力模型。

对前轴取转矩，根据转矩平衡，所以：

F2X4975=G1vX(4975-1850)+G2vX(4975-562)+G1hX1100+G2hX2014

其中：β为30%坡度，约等于16.7°。F2为后轴轴荷。 G1是整备质量，为16 850 kg。G1V是整备质量垂直与地面的分力，为G1×Cosβ(可求出G1V=16 139.3 kg)。G1h是整备质量平行与地面的分力，为G1×Sinβ(可求出G1h=4 842 kg)。G2是装载质量，为43 000 kg。G2V是装载质量垂直与地面的分力，为G2×Cosβ(可求出G2V=41 186.4 kg)。G2h是装载质量平行与地面的分力，为G2×Sinβ(可求出G2h=12 356.5 kg)。

带入公式，可求出F2=52 744.3 kg。

表2 传动轴状态分析结果

爬坡状态后悬架簧上质量增加为52 744.3-48 726.7= 4 017.6 kg。

可求出悬架在爬坡状态比在水平状态下沉11 mm，车桥仰角也发生变化，由2.9°变为3.5°。

2.2.4 、爬坡工况下传动轴夹角变化

在满载爬大坡工况时，车辆行驶需要较大的驱动力矩，此时发动机是接近全负荷运行的。因此动力总成质心会出现较大的位移，其位移值与动力总成悬置系统位移控制设计有关。从以上变速器输出法兰中心位移测量值可知，在满载爬大坡工况时，变速器输出法兰中心Z向位移，Y向位移均发生了较大变化，发动机倾角由2.83°变为4.3°。传动轴夹角校核见图13。

根据公式(2-1-8)，计算爬坡动态当量夹角为：

计算此时万向节角加速度幅值达到了1 140 rad/s2，远大于限值600 rad/s2的要求，相关转动轴爬坡姿态见表3。爬坡状态下，发动机的转矩接近全负荷运行，而且车辆坡道起步比水平地面起步，所用变速箱速比大了1.3倍，各种综合因素加起来，使万向节附加弯矩增加了近7倍；弯矩过大，造成了传动轴中间支撑、发动机悬置、中桥输入法兰等关联机件的振动，从而引发了整车抖动。

因得出结论：车辆在重载爬坡时，正是传动轴动态当量夹角超标，导致了车辆的爬坡抖动。

3 解决方案

找到了问题根源后，降低车辆爬坡状态的传动轴当量夹角，可有效解决车辆的重载爬坡抖动问题，目前笔者所在企业的市场改进方案是把传动轴合二为一，改为单节传动轴，长度为2 220 mm，同时为提高传动轴的极限转速，把轴管内外径做了加大处理，传动轴夹角状态见图14、15。

调整后传动轴当量夹角、最大摆角、角加速度幅值校核见表3。

目前该改进方案在市场上运行近1年，改进后效果良好，无抖动故障发生，客户反映良好。

表3 爬坡工况传动轴夹角状态

表4 调整后传动轴夹角状态

4 结论

通过实例分析，本文研究了由于传动轴系统布置设计有缺陷从而引起整车异常振动的原因，表明在商用车传动轴系统的设计布置中，除了常规工况下的传动轴当量夹角、最大夹角及角加速度幅值需满足设计要求外，还需增加满载爬坡工况下相关参数的校核，并使其满足设计要求，以避免因传动轴系统布置不当引起整车异常振动问题。

(注：孟凡生，男，1976年10月出生，工程师，北京福田戴姆勒汽车有限公司技术中心员工，从事商用汽车传动系统研究十余年)

[1]张洪欣 汽车设计[M]北京：机械工业出版社，1999，P106，P107，P109．

[2]王霄锋 汽车底盘设计；清华大学出版社，2010，P139．