1Cr18Ni9Ti钢管的常温蠕变性能

陈吉生，石晶辉，鄂大辛

（1.广州汽车集团股份有限公司汽车工程研究院，广州 511434；2.首都航天机械公司，北京 100081；3.北京理工大学材料科学与工程学院，北京 100081）

0 引 言

汽车工业的发展水平是一个国家发达程度的重要标志，而金属材料则是汽车工业发展的重要基础。金属管材具有轻量化以及良好的强韧性、吸收冲击性能等优点，广泛应用于航空航天、汽车制造等领域。低碳钢、高强钢和不锈钢等的管材在使用过程中，会出现以非热激活的粘滞性变形为特点的常温蠕变现象。与高温蠕变不同，常温蠕变的变形量随着时间延长而逐渐趋于饱和，因此单独的常温蠕变不会导致构件严重失效。但由于常温蠕变改变了材料内部、特别是裂纹尖端区域的应力应变分布，可能会对构件的应力腐蚀行为产生影响；加之测量仪器的精密化以及设备的微型化亦使得常温蠕变的影响愈加显著，故而相关的研究工作逐渐被人们重视［1－4］。国内对结构钢的常温蠕变现象进行了较多研究［5－8］，但有关1Cr18Ni9Ti钢管的常温蠕变性能以及常温蠕变对材料性能影响的相关报道很少。因此，作者对1Cr18Ni9Ti钢管进行了常温蠕变试验，分析了应力水平、加载速率和加载历史对其常温蠕变性能的影响以及常温蠕变和加载历史对其屈服强度的影响。

1 试样制备与试验方法

管材在服役过程中长期受到载荷的作用，容易产生常温蠕变行为。为更接近管材的实际服役状态，通常先对管试样进行不同程度的预拉伸变形后再进行常温蠕变试验。

1Cr18Ni9Ti钢管的常温蠕变试验采用微机控制电子式WDW－E100D型液压伺服万能试验机进行，该试验机可实现对应变速率等参数的有效控制。常温蠕变试验温度范围为（22±2）℃，采用标距为50mm的引伸计测常温蠕变应变。管试样的尺寸根据GB／T 228－2002选取非比例试样（原始标距Lo＝50mm，平行长度Lc≥100mm），原始管外径d0＝6mm，原始壁厚t0＝1mm，在同一原始管材上截取以减小管材制造公差及热处理工艺对拉伸试验结果的影响。为防止试样不在中心标距内断裂采用3重标矩，标距线与夹持线之间的距离设为12.5mm（大于d0）。断后标距优先选用中心标距。为尽可能保证加载过程中的单向受力状态，在试样两端塞入自制的伸入端带圆角的圆柱形硬质合金塞头，同时在塞头上包裹一层防滑胶带。管试样的结构和尺寸如图1所示。

图1 管试样的结构及尺寸Fig.1 Structure and dimension of tube sample

为研究不同试验参数和加载历史对常温蠕变性能的影响，采取如下试验方案：

（1）在预拉伸变形量ε为0.075、加载速率为14.8kN·s－1的基础上，对管试样进行应力分别为60%（154.8MPa），70%（180.6MPa），80%（206.4MPa）及90%（232.2MPa）屈服强度的常温蠕变试验，研究不同应力水平（σ）对常温蠕变性能的影响。

（2）在预拉伸变形量ε为0.075、恒载应力为232.2MPa的基础上，通过电子拉伸试验机将加载速率转换为1.85kN·s－1（29.0MPa·s－1）、3.7kN·s－1（58.1MPa·s－1）、7.4kN·s－1（116.1MPa·s－1）及14.8kN·s－1（232.2MPa·s－1）对管试样进行常温蠕变试验，研究不同加载速率对常温蠕变性能的影响。

（3）对管试样进行不同程度的预拉伸，预变形量ε分别为0.075，0.190，0.315。由于管试样经不同预变形后的屈服强度不同，因此在试验中将不同应变后管试样的90%屈服强度作为常温蠕变的恒载应力进行常温蠕变试验，研究预变形量对常温蠕变性能的影响。

（4）对预拉伸试样进行常温蠕变试验（一次蠕变），记录蠕变数据；卸载后，加载应力及加载速率保持不变，重新对该试样进行常温蠕变试验（二次蠕变），记录蠕变数据，研究不同加载历史对常温蠕变的影响。

此外，为研究常温蠕变对屈服强度的影响，采取以下三种不同的试验方案。（1）对管试样进行预拉伸，变形量ε为0.075，卸载后保持加载速率和加载应力不变，进行二次拉伸，变形量ε为0.150；（2）对管试样进行预拉伸，变形量ε为0.075，卸载后进行常温蠕变试验；常温蠕变试验卸载后进行二次拉伸，变形量ε为0.150；（3）对管试验进行常温蠕变试验，卸载后进行预拉伸，变形量ε为0.075，卸载后保持加载速率和加载应力不变，进行二次拉伸，变形量ε为0.150。

2 试验结果与讨论

2.1 应力水平对常温蠕变性能的影响

从图2可以看出，在试验应力水平下，1Cr18Ni9Ti钢管均发生了常温蠕变现象，且蠕变应变随着应力水平的增大而明显增大；当管试样在154.8MPa应力下加载时，可观察到较小的蠕变应变，蠕变应变的最大值仅为0.0008；随着应力水平提高，在206.4MPa应力下加载时这种时间相关的蠕变应变已经比较明显；当应力水平进一步提高至232.2MPa时，蠕变应变表现得更为显著，此时，在1800s内的蠕变应变累积量已接近0.0028。

图2 不同应力水平下1Cr18Ni9Ti钢管的蠕变应变－时间曲线Fig.2 Creep strain vs time for 1Cr18Ni9Ti steel tube at various stresses

实际上，常温蠕变是位错与时间相关的滑动过程。位错分为可动位错及不动位错，在载荷作用下，可动位错被激活而进行滑移，不动位错不仅不能进行滑移，而且对可动位错的滑移还具有阻碍作用。当可动位错经过位错运动自由行程的平均长度后，被不动位错捕获而成为不动位错。可动位错随时间延长而进行的滑移在宏观上表现为常温蠕变现象。位错的滑移速率与常温蠕变速率的关系见式（1）所示的 Orowan方程［9］。

此外，由晶粒内部的粘滞拖曳力控制的有效应力σe决定了可动位错的滑移速率和寿命，从而直接影响材料的常温蠕变变形程度，故有

式中：τ0为基体对位错拖拽作用的常数；n为应力－速率指数。

有效应力σe可用式（3）表示。

式中：σ为外加应力；a为位错强化常数；G为剪切模量；ρn为不动位错的密度。

由式（1）可以看出，可动位错的滑移速率和密度是影响常温蠕变速率的重要因素。对于特定材料，位错的滑移速率主要由作用在位错上的有效应力决定，如方程（2）所示。不仅外加应力水平对有效应力具有决定作用（呈正相关），而且不动位错的密度对其也有重要影响（呈负相关），如式（3）所示。因此，应力水平增大意味着有效应力及可动位错的滑移速率增大，常温蠕变应变随应力水平提高而迅速增加。

2.2 加载速率对常温蠕变性能的影响

由图3可见，在232.2MP应力水平作用下，常温蠕变应变随加载速率的增加而增大。在相同的应力水平下，总位错密度一定，可动位错密度增加的速率正比于蠕变速率，如式（4）所示。

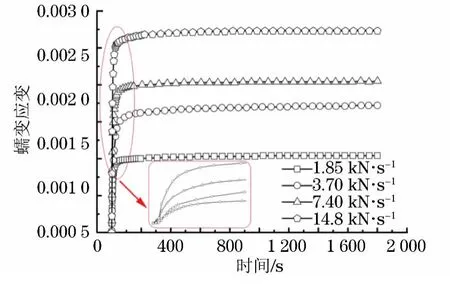
图3 不同加载速率下1Cr18Ni9Ti钢管的蠕变应变－时间曲线Fig.3 Creep strain vs time for 1Cr18Ni9Ti steel tube at various loading velocities

高的蠕变速率可产生更多的可动位错，较多的可动位错以相对较快的速率滑移，从而在宏观上表现为常温蠕变应变随加载速率的增加而增大。

此外，在试验过程中，由于存在应变硬化，故而可动位错占位错总量的比例下降［10］。由式（1～3）可知，初始的常温蠕变速率最大。随着蠕变的进行，可动位错逐渐陷入位错网络变为不动位错，从而使得可动位错的密度降低，不动位错的密度增大，同时不动位错的增加也使得有效应力降低，进而导致可动位错的滑移速率下降，因此常温蠕变速率随着蠕变的进行逐渐降低。

2.3 加载历史对常温蠕变性能的影响

除上述两个因素之外，试样加载前的加载历史也会对后续的常温蠕变性能产生明显的作用。由图4可见，常温蠕变应变因不同的加载历史而具有明显的差异。由于进行一次蠕变时，起始阶段不动位错的密度较低（仅预拉伸时的不动位错），可动位错的滑移速率较高，具有较大的常温蠕变速率；卸载后进行二次蠕变时，由于管试样已经历过一次蠕变，不动位错的密度高于仅经过预拉伸的的管试样，从而导致二次蠕变时可动位错的滑移速率降低。因此，在宏观上表现为二次常温蠕变应变显著减小，并且减幅随预变形量的增大而增大。

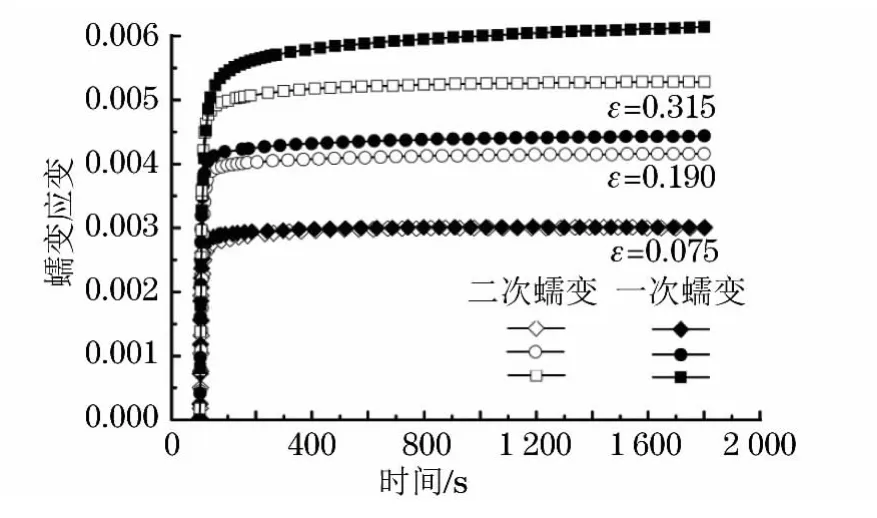
图4 二次蠕变下1Cr18Ni9Ti钢管的蠕变应变－时间曲线Fig.4 Creep strain－time curves of 1Cr18Ni9Ti steel tube at two－stage creep

2.4 常温蠕变及加载历史对屈服强度的影响

由图5可以看出，当管试样未经过常温蠕变时，加工硬化所获得的屈服强度增量为132.27MPa，而当管试样经过不同加载过程的常温蠕变后，屈服强度增量有所增大，屈服点处的屈服强度增量分别为176.79MPa和179.87MPa，即常温蠕变对材料产生了应变强化作用。

图5 常温蠕变及加载历史对屈服强度的影响Fig.5 Effects of room temperature creep and loading process on yield strength

管试样经一次单向拉伸、卸载之后继续进行二次拉伸后，其屈服强度并没有发生明显的突变（仍沿着屈服曲线变化）。这是因为在卸载后再加载的过程中，材料内部不动位错的密度没有明显变化，所以屈服强度没有明显变化。但是，当蠕变应变与预拉伸应变累加时，屈服强度会显著上升。这是因为在常温蠕变过程中，可动位错不断地被不动位错捕获，并陷入到位错网络中，明显提高了不动位错的密度，从而导致常温蠕变后再进行拉伸时屈服强度显著提高。

3 结 论

（1）1Cr18Ni9Ti钢管的常温蠕变应变随应力水平和加载速率的增大而增大，蠕变应变表现出明显的应力敏感性；当应力水平较低时，蠕变应变较小；当应力水平增大至232.2MPa时，蠕变应变约为0.0028。

（2）二次蠕变可提高不动位错的密度，阻碍可动位错的运动，从而使可动位错的滑移速率降低，在宏观上表现为二次常温蠕变应变减小。

（3）当试样经过不同加载过程的常温蠕变后，不动位错密度增加，之后再进行单向拉伸可使屈服强度有所提高。

［1］张敬文，鄂大辛，李延民，等.管材弯曲中起皱行为的试验及有限元模拟分析［J］.汽车工艺与材料，2011（5）：6－9.

［2］DAXIN E，CHEN Ji－sheng，DING Jie，et al.In－plane strain solution of stress and defects of tube bending with exponential hardening law［J］.Mechanics Based Design of Structures and Machines，2012，40：257－276.

［3］陈吉生，鄂大辛，张敬文.材料模型对1Cr18Ni9Ti管材拉伸有限元仿真的影响［J］.精密成形工程，2012，4（4）：10－12.

［4］吴海宏，郭正民.1Cr18Ni9Ti不锈钢丝蠕变机理及本构方程的研究［C］／／线材制品国际技术研讨会会议文集.北京：中国金属学会，2006：133－136.

［5］刘云旭，朱启惠，李兴仁.40CrNiMoA钢的常温蠕变规律及其影响因素［J］.吉林工学院学报，1992，13（3／4）：1－6.

［6］莫涛，赵杰，聂德福，等.0Cr18Ni9裂纹试样的室温蠕变现象及对裂纹扩展的延滞效应［J］.机械强度，2007，29（6）：997－1000.

［7］李建弘，李全安，张兴渊，等.汽车用抗蠕变镁合金的开发与应用［J］.铸造，2007，56（11）：1137－1142.

［8］杨楠林，谈建平，轩福贞，等.应力水平对In783合金蠕变性能和蠕变机制的影响［J］.机械工程材料，2014，38（3）：27－30，34.

［9］聂德福，赵杰，莫涛.X70管线钢的室温蠕变及其对流变应力的影响［J］.材料工程，2006（6）：58－61.

［10］杨晓光，石多奇.粘弹性本构理论及其应用［M］.北京：国防工业出版社，2013：141－142.