中美职前小学教师“教学用数学知识”的发展比较——以分数乘除法为例

段素芬，Xianwei Yuan Van Harpen

（1．淄博师范高等专科学校 数理科学系，山东 淄博 255130；2．University of Wisconsin-M ilwaukee, M ilwaukee, WI, U.S.A）

中美职前小学教师“教学用数学知识”的发展比较
——以分数乘除法为例

段素芬1，Xianwei Yuan Van Harpen2

（1．淄博师范高等专科学校 数理科学系，山东 淄博 255130；2．University of Wisconsin-M ilwaukee, M ilwaukee, WI, U.S.A）

中美职前小学教师对分数乘除法运算法则较熟悉，但知识的教学之用及发展存在一定差异：（1）知识方法维度：中国学生对分数乘除法运算的算法明确、结果准确，美国学生对分数乘除法的概念性理解有局限，有时出现一定偏差．（2）理解表征维度：美国学生的知识理解和表征是发散的、多样化的，中国学生的知识表征和运算方法则比较单一．中国学生倾向于数字和符号的计算，美国学生则关注和擅长于图形与问题情境的表征．（3）教学策略维度：中美学生的教学用数学知识有进步，但进步的幅度不大，美国学生的进步则更明显．中美学生对分数乘除法运算的程序性知识较好，但数学知识的教学实践之用是“捉襟见肘”的．

教学用数学知识；分数乘除法；职前小学教师；发展比较

1 问题提出

美国学者舒尔曼（Shulman）1986年提出[1]，教师在教学中仅有学科知识和教学知识是不够的，必须具有学科知识与教学知识的融合知识，也就是学科教学知识PCK（Pedagogical Content Know ledge）．PCK理论强调，教师能够“用学生易于理解的方法来表达学科内容的知识”，将所教的学科内容知识以学生易懂的方式加工、转化、表达并传授给学生．PCK的理论提出之后，引起了教育研究者的高度关注[2～3]．在具体的学科领域，如数学，就出现了数学学科教学知识（Mathematical Pedagogical Content Know ledge）[4～7]．著名学者范良火的研究指出[8]，教师教学知识的最重要来源是“自身的教学经验和反思”以及“与同事的交流”，而“作为学生时代的经验”以及“职前培养”却是最不重要的来源．这对职后教师培训与教师专业发展提供了重要的借鉴，却同时给教师教育的职前培养提出了深刻的思考：难道教师教育的职前培养在教师教学知识的专业发展中无能为力？无用武之地？

职前教师培养是教师教育的源头和起点，在教师专业成长与发展中具有基础而重要的决定作用．知识处于教师专业发展的核心地位，职前教师的专业知识决定着他们今后专业发展的基础和方向．当然，教师具有“学生易于理解、易于接受的方式或策略”的知识是无可厚非的，甚至是理所当然的，是教师专业发展中应着重努力的方向．但要想“用学生易于理解的方法来表达学科内容的知识”，教师首先要对所教学科内容知识有真正的专业理解，因为只有当教师深刻理解后，才有可能深入浅出地讲解，包括对学科概念、定理的形成过程，蕴涵的思想方法、本质含义，各知识命题之间的相互关系及严密的知识网络体系等等，要有深刻的、本质的理解，这在教师的职前培养中是需要重点达成的．Ball开创了“教学用数学知识”（Mathematical Know ledge for Teaching）的研究[9～10]．她指出，对数学知识性质的不透彻理解，将使世界范围内改善教师教育质量的良好意愿受挫[11]．为今后的教学做对教学有用的数学知识上的准备，这与沈文选教授提出的“教育数学”的思想（作为教育的数学）有一定的相近性[12]．

他山之石，可以攻玉．研究者从中外实践取向比较的视角来关注职前教师的教学用知识，更重要的是研究职前教师的教学用知识发展的比较．为了使比较有意义，比较单位之间应该有一定的相似性，惟其如此，才能使得研究内容表现出的差异更有意义．研究中选取的中美两国个案分别是中国山东一所师范高等专科学校和美国伊利诺伊州一所大学．中国的山东省乃是孔子文化的发源地，政治经济较为发达，教师教育亦属领先创新，这所师范高等专科学校已有六十多年的建校历史，为省内外培养了无数优秀的小学师资，是山东省教师教育基地．美国的伊利诺伊州是美国经济、政治和文化都相对发达的一个地区，伊利诺伊州的教师教育在美国也位于发端之列，这两所高校的小学教师教育都能较好地代表两个国家小学教师教育的水平．

2 概念界定

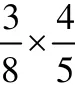
3 研究设计

3.1 研究对象

近年来，尽管大量的研究者做了对教学知识的研究，但由于时间和地域的原因，对中美两国职前小学教师的比较是很少的．这里将涉及两国高校小学教师教育大学新生和毕业班的学生，尽管这样的选择比不上跟踪同一批学生在整个高师教育过程中的进步情况，但由于时间的限制，这种选择将在最大程度上体现高师小学教师教育对职前小学教师教学知识的影响．

对中美职前小学教师教学用数学知识的发展比较，是通过调查大学新生和临近毕业的师范生来实现的．中国被试是山东省一所师范高等专科学校的数学教育专业（小学教育方向）的师范生，美国被试是指伊利诺伊州一所大学的小学教育专业的师范生．在两国的两所高校分别选取两个年级的师范生，共发放400份问卷，收回有效问卷373份．373名调查对象中，中国大学新生96名，毕业生89名；美国大学新生100名，毕业生88名．

3.2 研究内容

研究教学用知识必然涉及到具体的学科知识内容．张景中院士曾提到：教育数学可以着眼于两点——难点和新点[14]．分数作为学生在学习了整数的概念与运算基础上的新点，更是小学生学习过程中遇到的最为复杂的概念之一[15]，当属小学数学教与学的难点，理所当然成为职前小学教师准备的重点．有研究表明，教师对于分数概念与运算的学科教学知识状况让人堪忧．Post等对小学教师研究表明，约有四分之一教师在分数基本运算上存在困难；Stoddardt对小学职前教师研究发现，半数教师无法正确解决分数乘除法的问题；Li等研究表明，93%的职前教师能正确计算分数除法，但将问题换一种问法（如四分之三里面有几个二分之一？），则正确率降低至52%；Ball研究了教师教学分数除法表达式的能力，发现教师仅仅知道计算规则和程序，却不能把这种程序性知识转化成有助于学生理解的形式．Orton研究了分数概念的表达，发现大多数教师严重依赖于程序性的符号表达式，而不是依赖于有助于理性认识的表达方式[16]．这说明教师在理解分数概念和分数运算的意义上存在困难，在数的运算概念与运算程序上存在着知识和理解的间断性和不完整性[17]．

借鉴以上研究，以分数乘除法为例，对中美职前小学教师的教学用数学知识的发展状况进行调查比较，具体是：（1）中美两国大学新生对分数乘除法的认识和理解．（2）中美两国毕业生对分数乘除法的认识和理解．（3）中美两国师范生对分数乘除法认识和理解的发展状况的差异．

3.3 研究方法与过程

研究通过问卷调查法与访谈法，以中美职前小学教师为研究对象，针对分数乘除法运算知识，通过两个情境题（分别围绕分数乘除法设计，情境题要求师范生设想在特定的小学数学教学环境下教授分数的乘除法知识），对他们的教学用数学知识进行了比较．依据教学用数学知识的内涵，考虑知识评价框架，分别在知识方法维度（一般的数学知识）、理解表征维度（一般的教学知识与深刻的教学知识）和教学策略维度（联系的数学知识与深刻的教学知识），对中美两国职前小学教师的掌握情况及其发展状况进行比较分析．

在参考有关专家的研究工具的基础上[18]，研究者自行设计了调查问卷．采取集中调查的方式，在两国两所高校请调查对象在统一时间和地点填写问卷，时间以保证调查对象能够完成全部题目为准．2011年春季，研究获得美国IRB的批准；2011年秋季，对中美大一新生进行了调查，并进行了访谈录音；2012年春季，进行了中美两国毕业生的调查，并进行了深度访谈．

问卷收回后，对每道情境题的回答进行得分级别编码和赋分．两道情境题除了做不同得分级别的编码，还对答案类型编码，由中美两名研究者分别编码．首轮编码后，两道情境题的编码的一致性分别为96.6%、97.4%，随后对编码不一致的题目答案进行审议，直至得到一致的编码结果．所有数据采用软件SPSS13.0进行录入、处理与分析．

4 结果与分析

4.1 分数乘法的比较

情境一：人们通常会这样求解分数的乘法：

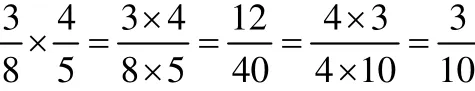
设想您是一位小学数学老师，您会怎样给一个五年级的小学生解释另外一种求解以上乘法的方法？

情境一回答类型与人数描述统计及相关研究如表1～表3所示．

表1显示，中美两国师范生中选择先约分再相乘或先相乘再约分方法的人数是最多的，这也是大多数人在面对分数乘法时使用最为普遍的方法．其中，从A、B策略中，可以看出中国学生明显注意到约分能使计算简单，美国学生大部分是计算到最后才约分，这样在计算过程中就要应付较大的数字．这可能体现出中国老师在教育中更注重计算的速度和正确性．从策略C可以看出，两国学生都有明显进步，而美国学生进步更大，体现出很多新生甚至不知道什么叫“解释另外一种方法”．到了毕业生，大部分学生都较明确．从策略F可见，美国毕业生采用画图解释人数是最多的，这是美国毕业生的显著不同之处，中国毕业生没有几个能这样想的，原因主要在于美国师范生的课程里强调画图．研究者认为，策略F和G是最能帮助小学生理解分数乘法概念的解释，美国学生在这两种回答上都超过中国学生，但是人数仍然很少．总之，中美师范生显然对常规分数乘法运算的法则都比较熟悉，但中国学生的熟悉度明显更高．在知识方法维度，中国学生解题正确率极高而且方法高度一致，而美国学生解题方法多样，但正确率较低．虽然约分法也是毕业生中使用最多的方法，但总体来讲，毕业生使用的方法策略稍多于新生．在理解表征维度：美国学生具有发散的、多样化的知识理解和表征，尽管有时具有一定偏差；而中国师范生的教学用知识虽然比较准确，但知识的呈现和运用较为单一．这也显示出美国文化教育的注重个性化与创新性，相对而言，中国是比较“整齐划一”的．在教学策略维度：美国毕业生做得较好，有近四分之一的人用画图的方式来解释分数乘法运算，有近十分之一的人用加法详细解释分数乘法运算的本质，这在所有的调查对象中比例是最突出的．

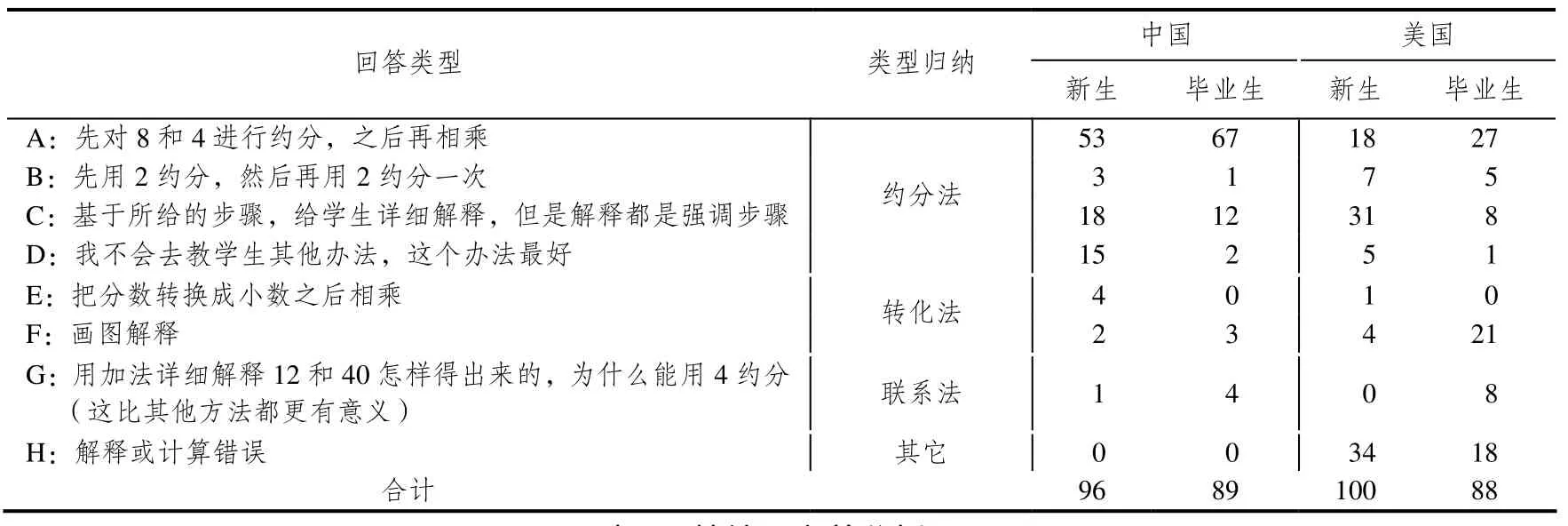
表1 情境一回答类型与人数描述

表2 情境一方差分析

表3 情境一多重比较

由表2可以看出，中美师范生对分数乘法的运算策略具有显著性差异．表3显示，中国两级师范生、美国两级师范生各自之间的差异不显著，p值均大于0.05的显著性水平．但中美新生之间、中美毕业生之间的差异较显著．具体是美国毕业生中有较多的人数用画图方法解释或表征分数的乘法，有的毕业生将分数乘法的理解联系到乘法就是加法的实质意义上来解释，这是美国毕业生在情境一的亮点．这说明，美国毕业生已经能够使用普遍方法之外的其他表征，并能从分数乘法的本质意义上来解释算法的合理性，也即能将算法联系到本原的算理意义上．这一点，比较可贵，体现了美国毕业生在教学用数学知识上的进步．相比较而言，中国的学生却稍逊，中国学生都很少使用约分之外的其它解释或表征方法．访谈中，中国毕业生认为，题目会做而且做对是没有问题的，但作为毕业生是很少考虑知识本原的理解以及面向小学生的教学用的知识．

4.2 分数除法的比较

情境二：问题(a) 人们在做分数的除法时方法不一．您会怎样解答以下这个除法？

问题(b) 设想您是一个小学数学老师．为了使学生理解数学的意义，很多老师会用现实世界中的情境或者故事来帮助学生看到某一数学内容日常生活中的应用．您能给上面这个除法运算编一个好的故事吗？

4.2.1 问题（a）的比较

此情境使用了马力平的测试题目，考查学生对分数除法的运算和理解．在小学数学中，分数被认为是最复杂的数，分数除法被认为是对最复杂的数作最难的运算．对问题（a），中国绝大部分学生的解答方法是首先将被除数的带分数转化成假分数，然后将分数除法转化成分数乘法，最后按照分数乘法法则进行计算，而且中国学生的计算结果几乎都正确，只是几个学生没有将最后结果进行化简约分．美国学生计算分数除法的程序性知识就远远不如中国学生，他们有的是思路正确，但结果错误；有的是思路本身就有误；有的是带分数转化成错误的假分数；有的是分数除法转化成错误的分数乘法；有的是分数乘法出现错误，有的是最后结果没有约分化简，关于师范生回答策略与人数描述的统计见表4．

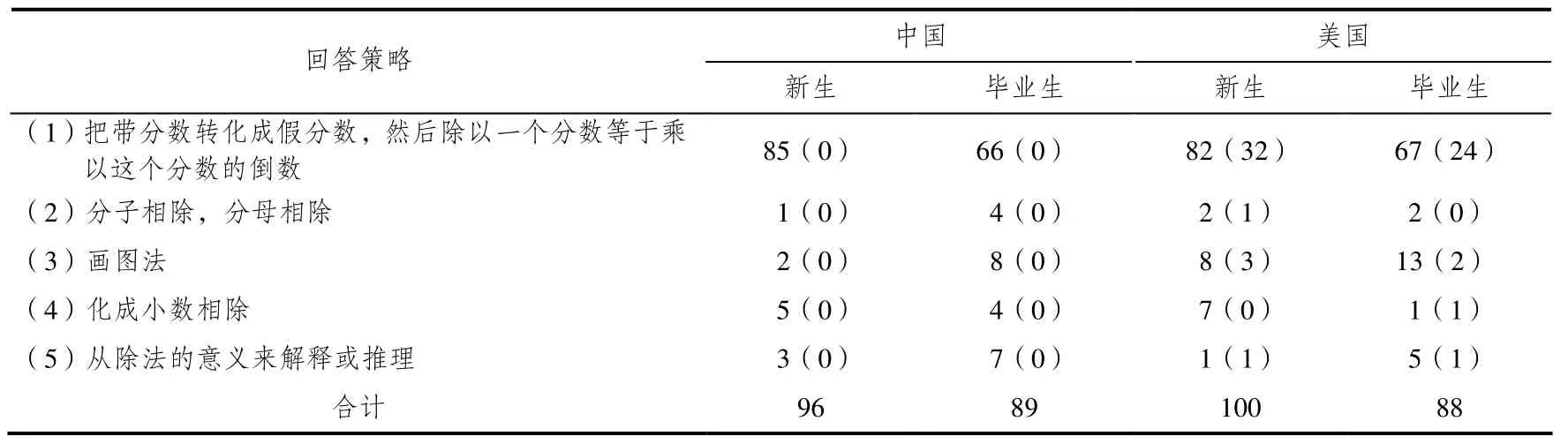
表4 情境二（a）回答策略与人数描述

表5 情境二（a）成对样本检验（显著性水平α=0.05）

4.2.2 问题（b）的比较

为了使学生理解数学的意义，很多老师会用现实世界中的情境或者故事来帮助学生看到某一数学内容在日常生活中的应用．中国学生编出了多种多样的文字题目，绝大部分是具有一定实际意义的．而美国学生几乎很少编出，写出想法的少数学生也在分数的意义、分数除法的意义上出现了错误，但美国学生编的文字题的实际背景的范围却比中国学生的宽泛．这个情境问题是中美学生差异最大的一个题目．这表明中国师范生对分数除法的运算法则、通分约分的运算有非常好的程序性知识的掌握，但中美新生与毕业生所使用的方法略有区别．情境二（b）回答类别及百分比描述见表6．

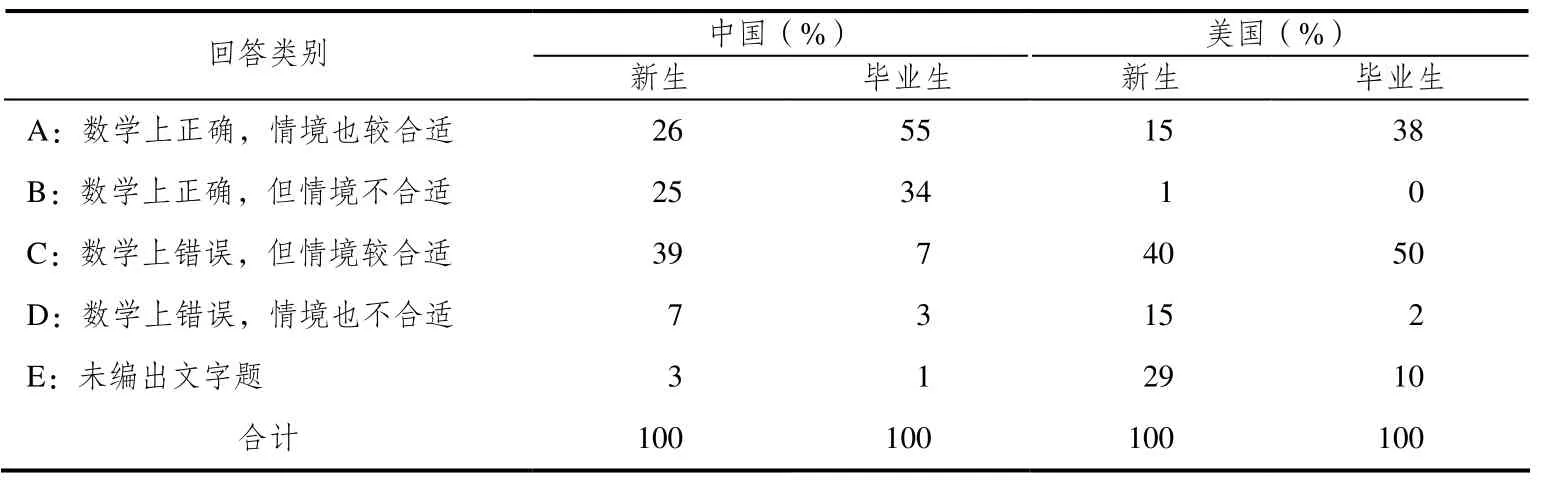
表6 情境二（b）回答类别及百分比描述

从表6可以看出，中美师范生编制的分数除法的文字题错误率较大，有的是数学上出错了，有的是问题情境不合适．中国总样本的正确率为43.8%（仅指所编文字题目数学上正确，情境也较合适的．比如：小明的爸爸买了3份一样的蛋糕，爸爸吃了一份不够，又吃了另一份的3/4，小明吃了一份的1/2，问：爸爸吃的是小明吃的多少倍？），中国大学新生和毕业生的正确率分别为26%和55%，相差29个百分点．美国总样本的正确率是28.2%，（例如：A person has to walk (1 and 3/4) of a m ile around a ½ m ile track. How many times does he need to walk around to get (1 and 3/4) mile?）美国新生和毕业生的正确率则更低，分别为15%和38%．这一点上，中美师范生的差异是比较显著的（见表7）．情境二（b）回答错误类别示例见表8．

表7 情境二（b）方差分析

表8 情境二（b）回答错误类别示例

表8是中美职前小学教师情境二（b）回答错误类别示例．值得一提的是，在错误类别B中，中国新生占25%，毕业生占34%；而美国新生仅占1%，美国毕业生更是0．这说明中国学生更多地倾向于数学上计算性的熟悉，而对计算背后的情境支撑则不太擅长；相反，美国学生编的文字题目更看重情境性里的数学．与此一致的是，在错误类别C中，美国毕业生（50%）比中国毕业生（7%）高出43个百分点．从这两个错误类别中可以明显看到，尽管中国学生的正确率高于美国学生，但中国学生关注且擅长于数字和符号的计算，相反美国学生关注且擅长于问题情境的表征，这也是中美学生在数学学习中的一个比较显著的差异．另外没有编出文字题的师范生中，美国学生较多（新生29%，毕业生10%）．该情境题目主要分析分数除法的含义以及分数除法与乘法的关系入手，处理错误的师范生在这方面存在困难．

5 结 论

针对分数乘法和除法运算，访谈中，学生对分数乘法和除法的计算法则几乎都能流利说出，但问及计算法则的意义，则理解欠佳，不能将乘法是加法的简便运算，以及除法是乘法的逆运算的道理联系起来．但相对来说，中美毕业生的理解是优于大学新生的．

5.1 教学用数学知识是有进步的但进步的幅度不大

从分数乘除法的情境题来看，中美毕业生的教学用数学知识的使用意识相对大学新生是比较明确的，这体现在：分数乘法中，在画图与利用加法来解释乘法的意义时，毕业生对于分数乘法的本质意义的理解是优于新生的；分数除法中，也是在画图与利用分数除法的本质意义来解释运算的法则，毕业生的理解也是优于大学新生的；而编制适当的分数除法的文字题，毕业生在“数学上正确，情境也较合适”更胜于大学新生，他们能够从数学上把握分数除法的正确性，还能将分数除法的意义放在合适的语境中使小学生学习和掌握．

此外，大学新生大多使用符号表征，较少使用言辞表征，毕业生则综合使用了言辞表征或符号表征，能够使用适当的语言解释或说明符号、图形、表达式的意义．横向来看，美国师范生使用直观表征要好于中国学生，这表现在美国学生更倾向于用画图的方式来解释分数乘除法，尽管他们在解释中出现了不同的错误．中国学生虽然计算正确，却高度一致地使用符号表达式来进行分数乘除法的法则运算，其中也有很少的围绕写出的运算表达式进行语言解释．研究发现，在使用言辞表征和符号表征的师范生中，使用固有的分数乘除法的运算法则去解释这两个情境问题的人数是比较多的，大学新生尤为突出．师范生对于分数乘除法运算法则的程序性知识非常熟悉，并非他们对运算法则理解较为深刻，而是先前的学习经验和学习基础只“记住”了法则之下的如何进行分数的乘除法运算，正如学生在访谈中所言：“我们对分数乘除法的运算法则根深蒂固”，但就是这样“根深蒂固”的知识，是否可以采用不同的表征和策略加以解释或理解，师范生们却“望而却步”．可见，师范生对于算法的理论依据——算理并非真正理解，大多停留在“算法”的方法操作层面上．

5.2 教学用数学知识的理论形态尚可但实践形态欠佳

研究表明，师范生的教学用数学知识带有明显的传统知识的色彩，无论是毕业生还是新生，大部分学生对分数乘除法的运算法则比较熟悉，即使在运算操作的过程中有时是有误的，但作为未来小学数学教师来讲，更丰富、更系统的关于分数乘除法的教学操作与实践形态的知识则是比较欠缺的．这表现在毕业生在处理分数乘除法运算的方法和策略，比新生做得要好，他们更多地使用画图以及从乘除法的本质意义上去解释运算的合理性，而美国毕业生在画图方面则表现更为突出，但总体来讲，这部分毕业生所占比例却很少，虽有意识但不具有普遍性．在分数除法文字题的编制中，毕业生把分数除法的意义放在合适的语境中做得也是比较好的．遗憾的是，毕业生虽然显现了一定的教学用数学知识的意识以及应用，但这部分的比例尚小，毕业生虽然能从分数乘除法的本质意义上去进行运算，但面对具体的分数乘除法知识，作为小学数学教师面对教学时的具体实践知识是比较欠缺的．这种情形表面上类似于“茶壶里煮饺子——有口倒不出”，但实际上师范生对于分数乘除法的本质意义的理解还是不到位的，即学生感受到了情境却可能没有体会到分数概念的必要性以及分数运算的意义，顺利地进行了操作活动却可能没有涉及分数的本质[19]．这表现在毕业生面对分数乘除法的教学时，仍很大比例的将运算法则直接教给小学生，而考虑小学生的学习心理以及接受知识的表征方式却很少．毕业生仍将教学用数学知识大面积的理解并应用于“运用法则、求出结果”即可，只是将所教知识“是什么”教给了小学生，而“为什么”、“怎么样”却很少涉及，甚至是在教学中“置之不理”．这种所谓的“理论”，面对教学实践之用是“捉襟见肘”的．

6 启示与思考

教师教育的职前培养是面向未来的教师，是为未来教师的知识和技能做准备的，其宗旨是培养未来教师的“教的知识和教的能力”，而教学用的知识则是教师从教知识与能力的综合体现，它不但要求教师要解答和学生一样的数学题，还要求教师分析学生的特殊解法，更要求教师对数学知识或关系做出合理解释．针对具体的分数乘除法来说，职前教师要准备的不单单是算法，更要准备算理，算法和算理是相辅相成的，算理是算法的理论依据，算法是算理的提炼和概括[20]．目前美国的课程体系比较注重数学的基础性和与数学的纵横联结[21]，而中国高师教育的课程方案中都包含具体学科的知识以及教育学心理学的知识，但关于学科知识与教学知识的融合却比较少，或者说是成效不彰．虽然有小学数学课程与教学论、小学数学教学案例、小学数学教学研究等数学与教育学融合的课程开设，但师范生教学用的数学知识却根基不牢、本质不清，如何在高师教育中彰显教学用学科知识的效力，真正发挥教师教育职前培养的功能，是当前亟需解决的现实问题．

从重视基础教育，到关注教师教育，再到重新审视教师职前教育．研究者认为，职前小学教师培养是一个战略上关键的阶段．在这个阶段中，职前小学教师应该发展对小学数学基础知识的深刻理解，应该发展对“教学用数学知识”的本质理解，应该发展基础数学与高等数学之间的联系知识．尽管中美职前小学教师对教学用的数学知识存在一定差异，但总的来看，职前小学教师对学科知识与学科教学知识的构建却都存在着不同程度的缺失．小学数学作为数学学习的开始，为进一步学习数学或教学数学打下了“根”与“源”的基础．作为职前小学教师的准备，应重视初等数学的基础性与高等性之间的联系，从而加深对数学基础知识的深刻理解，不仅仅是对小学数学有很好的概念性理解，而且还包含对小学数学内在的概念结构和基本的数学态度的掌握．

[1] Shulman L. Those Who Understand Know ledge Grow th in Teaching [J]. Educational Researcher, 1986, 15(2): 9.

[2] 李广，徐哲亮．近三十年来国外教师PCK研究的述评[J]．教育导刊，2013，（5）：48-52．

[3] 刘璇艳．国内关于学科教学知识（PCK）的研究综述及其对师资培训的启示[J]．中学数学杂志，2010，（12）：12-15．

[4] 陈子蔷，胡典顺，何穗．中国目前MPCK研究综述[J]．数学教育学报，2012，21（5）：19-22．

[5] 李渺，万新才，杨田．初中农村教师MPCK状况及来源的调查研究[J]．数学教育学报，2012，21（3）：35-38．

[6] 童莉．数学教师专业发展的新视角——数学教学内容知识（MPCK）[J]．数学教育学报，2010，19（4）：27-31．

[7] 李渺，宁连华．数学教学内容知识（MPCK）的构成成分表现形式及其意义[J]．数学教育学报，2011，20（2）：14-18．

[8] 范良火．教师教学知识发展研究[M]．上海：华东师范大学出版社，2003．

[9] Ball D L. Know ledge and Reasoning in Mathematical Pedagogy: Examining What Prospective Teachers Bring to Teacher Education [D]. East Lansing, M ichigan: M ichigan State University, 1988.

[10] Ball D L. Prospective Elementary and Secondary Teachers’ Understanding of Division [J]. Journal for Research in Mathematics Education, 1990, 21(2): 132-144.

[11] Ball D L, Bass H.Toward Practice-based Theory of Mathematical Know ledge for Teaching [R]. In: Davis B, Smm t E. Proceedings of the 2002 Annual Meeting of Canadian Mathematics Education Study Group.

[12] 沈文选．走进教育数学[M]．北京：科学出版社，2009．

[13] 徐章韬，顾泠沅．面向教学的数学知识[J]．教育发展研究，2011，（6）：59-63．

[14] 张景中，曹培生．从数学教育到教育数学[M]．北京：中国少年儿童出版社，2005．

[15] Boulet G. Didactical Implications of Children’s Difficulties in Learning the Fraction Concept [J]. Focus on Learning Problems in Mathematics, 1998, 20(4): 19-34.

[16] 赵冬臣，马云鹏，李业平，等．职前小学数学教师教学知识状况调查[J]．数学教育学报，2010，19（4）：48-52．

[17] 柳笛．美国数学教师学科内容知识的研究述评[J]．数学教育学报，2010，19（6）：78-82．

[18] 马力平．小学数学的掌握和教学[M]．李士锜，吴颖康译．上海：华东师范大学出版社，2011．

[19] 曹新．“分数的初步认识”中的多元表征学习问题[J]．教育学术月刊，2013，（12）：72-77．

[20] 徐章韬，陈矛．算法化视角下中学数学教学内容的知识分析[J]．数学教育学报，2013，22（2）：11-14．

[21] 周莹，蔡金法．美国综合大学中学数学教育专业的课程设置探析[J]．数学教育学报，2011，20（5）：74-77．

Comparison of Development of Pre-Service Elementary School Teachers’ Mathematical Know ledge for Teaching in China and The United States——W ith the M ultiplication and Division of Fractions as an Example

DUAN Su-fen1, Xianwei Yuan Van Harpen2
(1. Department of Mathematical Sciences, Zibo Normal College, Shandong Zibo 255130, China; 2. University of Wisconsin-M ilwaukee, M ilwaukee, W I, U.S.A)

The pre-service elementary school teachers are fam iliar w ith the algorithm for multiplication and division of fractions whether in China or America, but the use of know ledge in teaching and its development are different: (1) Know ledge Method dimension. For Chinese students, they are clear about the algorithm for multiplication and division of fractions and their computation results are correct. The American students’ comprehension of its concept has lim its and sometimes has deviation. (2) Dimension of understanding representation. The American students’ understanding of know ledge and representation are divergent and diversified. For Chinese students, their understanding of know ledge and representation are heterogeneous. Chinese students are skilled in the calculation of numbers and symbols. The American students are supposed to be good at representing the problem situation. (3) Dimension of teaching strategy. American and Chinese students’ mathematical know ledge for teaching is extending, but the extending level is modest. By contrast, The American students’ progress is evident. Both of them have preferable procedure know ledge of the operation of the multiplication and division of fraction, but their mathematical know ledge for teaching practice is deficient.

mathematical know ledge for teaching; the multiplication and division of fractions; pre-service elementary school teachers; the Comparison of development

G40-059.3

：A

：1004–9894（2015）01–0038–07

[责任编校：周学智]

2014–10–05

山东省教育科学“十二五”规划课题——小学教师教育U-S合作课程资源开发研究（2013GG216）；淄博师范高等专科学校教学改革项目——基于学科教学知识视角的师范生教学能力培养的研究与实践（12JG004）

段素芬（1974—），女，内蒙古乌兰察布人，副教授，硕士，主要从事数学教育和教师教育研究．