学生“数学素养”指标的理论分析

何小亚

学生“数学素养”指标的理论分析

何小亚

（华南师范大学 数学科学学院，广东 广州 510631）

国内外的数学素养观主要分为“知识”取向、“知识+能力”取向和“多维度”取向3种；“多维度”取向的数学素养观存在3个缺陷；数学素养是指满足学生自身发展和社会发展所必备的数学方面的品格和能力，是数学的知识、能力和情感态度价值观的综合体，其构成要素包括数学运算、数学推理、数学意识、数学思想方法和数学情感态度价值观；数学素养可以由低到高分成数学知识和技能、数学过程和方法、数学情感态度价值观这3个层次；数学素养的行为表现是，理解基本的数学概念和原理，具备一定的运算、抽象、推理能力，能运用数学解决问题，会用数学语言来表达和交流，形成良好的数学情感态度价值观．

数学素养；内涵；构成要素

1 导 论

虽然数学新课程改革实施了十余年，但“知识+解题能力”的应试教育依然大行其道，素质教育仍然没有得到真正落实．究其原因，除了以笔试成绩作为评价学生数学表现的唯一标准的评价方式没有真正改变这一核心因素外，数学课程、数学教学中数学素养的缺失是另一大原因．尽管2011年新修订的九年义务教育数学课程标准[1]中有4处，高中数学课程标准[2]有10处出现了“数学素养”这一术语，但无论是课标还是课标解读[3～4]都没有对数学素养的内涵与外延进行界定，导致数学素养的培养无法具体落实．即将启动的高中数学课程标准修订需要数学素养顶层设计的指导．所以，数学素养内涵的界定，数学素养的构成，各个阶段数学素养的具体要求成了亟待解决的问题．

采取文献分析和系统分析的方法对相关数学素养研究进行梳理，最后回答以下3个问题：

问题1：什么是数学素养？

问题2：数学素养由哪些要素构成？

问题3：数学素养的具体要求有哪些类别？

2 国内外数学素养研究梳理

文献的收集基于两条线索：一是学生的数学素养研究；二是学校培养未来公民的数学素养研究．不考虑数学教师的数学素养研究．下面，按照国内与国外两条线索进行梳理．

2.1 国内数学素养内涵的界定与构成要素研究

根据心理学的理论，“素质”既有先天的条件，又有后天的养成，而“素养”则只是后天学习获得的结果，即素质包含素养．因此，将数学素质的研究文献归于数学素养的研究．

国内数学素养的研究可分为3个阶段（康世刚，2009）：

第一阶段（70年代末以前）：没有明确提出“数学素养”的名词，只是讨论与数学素养相关的问题，如（1）双基教学；（2）三大能力培养；（3）数学与实际生活的紧密联系；（4）数学史教育；（5）提高数学学习兴趣等．

第二个阶段（70年代末到1983年以前）：使用了“数学素养（素质）”的名词，但没有给予明确的定义．从使用“数学素养”的话语中可以发现，数学素养有这样的涵义：（1）进一步学习和研究数学的能力；（2）数学应用能力；（3）把数学素养作为教学目的与掌握数学思想方法；（4）扩展数学知识视野．

第三个阶段（1983年以后）：把数学素养（素质）作为一个研究对象，直接讨论数学素养的涵义．特别是在数学教学大纲中提出“提高学生数学素养”之后，把这一研究推向高潮．这一阶段涌现出3种研究思路：（1）从数学角度解释数学素质．（2）素质教育思想指导下的数学素养教育．

（3）如何在数学学科中落实素质教育思想[5]．

下面仅介绍第三阶段的研究情况．

2.1.1 国内学者对数学素养内涵的界定与分类

国内对数学素养内涵的界定主要有两类：

第一类是由素养（或素质）概念出发，演绎出“素养（或素质）＋数学教育术语”式的定义．例如，“MA”课题组（1997）：“数学素养是指以人的先天生理特点为基础，在后天的环境和数学教育影响下形成并发展的心理方面的稳定属性．”[6]

张建良等（2005）：“数学素养，是指在个人的先天素质的基础上，受后天教育与环境的影响，通过个体自身的学习、认识和实践活动等所获得的数学知识、数学能力和数学思想观念等的一种综合修养，我们也称之为数学品质．”[7]

王子兴（2002）：“数学素养乃是数学科学所固有的内蕴特性，是在人的先天生理基础上通过后天严格的数学学习活动获得的、融于身心中的一种比较稳定的状态．”[8]

显然，第一种定义方法忽视了数学学科本身的特殊性，没有真正揭示出数学素养的内涵．

第二类考虑到了数学学科的特殊性，从数学素养内涵的一个或几个方面来界定数学素养．主要表现为以下3类数学素养观：

（1）“知识”取向的数学素养观．

“知识”取向的数学素养观把数学知识作为数学素养的核心内容，较少考虑其它因素．

谢恩泽（1991）认为，数学素养指一个人拥有的相应的数学内容知识，如算术、代数、几何、分析等[9]．

郑强等（2006）认为，数学素养是在数学课程学习过程中，学生通过数学知识的学习，内化数学文化的成果，最终在自己身上体现一种新的价值或达到新的水平．这一观点虽然强调了数学知识是数学素养的重要内容，但它并非只是简单的数学知识，还包括了数学文化的内容[10]．

（2）“知识＋能力”取向的数学素养观．

“知识＋能力”取向的数学素养观把数学素养看成是一种能力或知识与能力的综合．

束仁武（1997）认为：数学素养主要指运算能力、发展逻辑思维能力和空间观念，辨别、猜想能力等[11]．

刘俊先（2009）认为，数学素养是指人们灵活运用数学的理论与方法，观察、分析、解决问题的能力[12]．

苏洪雨等（2010）认为，数学素养指的是对数学知识的理解以及进行数学教学活动过程中所展现的数学思想方法和数学能力[13]．

（3）“多维度”取向的数学素养观．

“多维度”取向的数学素养观，除了知识、能力之外，还考虑到了数学素养的其它因素．

朱德江（2004）认为，数学素养就是人们通过数学教育以及个体自身的实践和认识活动，所获得的数学知识、数学技能、数学能力、数学观念和数学思维品质等方面的素质与修养[14]．

王子兴（2002）认为，数学素养（也称之为数学品质）为数学知识、数学能力和数学思想观念等的一种综合修养[8]．

姚丽行（1995）认为，人的数学素养在日常生活中表现为：在学习数学中形成的良好的个性品质；能自觉地用数学知识和数学思想方法去观察、分析、处理周围的生活和生产问题；语言表达准确、简练、逻辑性强，具有较好的数学语言交流能力[15]．

张奠宙教授研究小组（1994）提出，数学素质应包括下面4个“层面”：

知识观念层面：能用数学的观念和态度去观察、解释和表示事物的数量关系、空间形式和数据信息，以形成量化意识和良好的数感；

创造能力层面：通过解决日常生活、实际情境和其它学科问题发展提出数学模型，了解数学方法，注意数学应用的创造型数学能力，并形成忠诚、坚定、自信的意志品格；

思维品质层面：熟悉数学的抽象概括过程，掌握数学中的逻辑推理方法，以形成良好的思维品质与合理思维习惯；

科学语言层面：作为一种科学的语言，数学也是人际交流不可能缺少的工具，数学素质应包括能初步运用这种简约，准确的语言[16]．

康世刚（2009）认为，基于对数学素养具有境域性、个体性、综合性、外显性以及生成性的本质属性的认识，从数学素养生成的角度把数学素养界定为：数学素养指主体在已有数学经验的基础上，在数学活动中通过对数学的体验、感悟和反思，并在真实情境中表现出来的一种综合性特征．广义的讲是一种综合性特征，狭义的讲，是指在真实情境中应用数学知识与技能理性地处理问题的行为特征[5]．

潘小明（2009）没有给出数学素养的内涵，但建议对数学素养的认识应该从数学活动的视角、全球教育的视角去分析[17]．

刘喆（2011）认为：数学素养是在数学经验积累的基础上，生成并外显出来的可用于指导特定背景或区域中数学活动的一种整体性思想和行为特征，这里的思想和行为特征主要是通过数学知识、数学能力和数学情感表现出来的[18]．

2.1.2 国内“多维度”数学素养要素的研究

按照研究成果发表年份的先后顺序，列出国内主要“多维度”数学素养要素的研究（见表1）．

表1 “多维度”数学素养要素的研究

有一些研究是从数学学科分类的角度来研究数学素养．比如说，代数素养、几何素养、统计素养、概率素养．目前，基于这一视角的研究，国内已经有两篇博士论文．

苏洪雨（2009）：几何素养的内涵主要因素包括：几何知识、几何能力、几何应用和几何背景，两个次要的因素：几何学习态度和几何文化[34]．

桂德怀（2011）：中学生代数素养的理解主要集中在五个维度：代数基础知识、基本技能、基本思想方法、基本能力和初步应用意识．其中，基础知识主要是指符号、规则和关系；基本技能是指运算、推理和可视化；基本思想方法主要包括化归思想、方程思想和函数思想；基本能力主要是指抽象概括能力、符号化能力和一般化能力；初步应用意识主要包括发现关系、建立模型、求解反思3个方面[35]．

此外，徐德均（2011）认为，南通中学之所以院士辈出，主要的原因是实施了“诚恒治学、积健为雄、名师垂范、激趣励志、导学精进、文理兼修”的数学素质教育[36]．

2.2 国外数学素养研究梳理

国外研究大致通过两种方式揭示数学素养的内涵，一是直接下定义；二是用对具备数学素养的人的描述来间接地解释这一概念．从国际视野的角度来看，数学素养的内涵发展可以分为3个阶段（刘喆，2011）：

第一阶段（20世纪60至80年代中后期），是数学素养提出的早期阶段，人们已经认识到数学素养在个人日常生活中具有重要作用，但它的内涵还比较狭窄，偏重于数量运算、估算能力和解释图表等所含数学信息的技能．

第二阶段（80年代末期至90年代末期），是数学素养的内涵不断拓展与丰富阶段，既突出强调在家庭、工作场所、社区等生活背景中发挥数学素养的作用，也初步凸显出数学素养是知识、技能和观念的集合体（但是，1994年IALS的定义却有所退步）．其中，知识涵盖了数学思想方法；技能也由数、量的运算层面拓展到几何、概率、统计等的推理、证明、测量层面，包括数学交流、问题解决和自我监控能力等；观念则有懂得数学价值、理解和欣赏数学本质、对自己的数学能力有信心等．

第三阶段（21世纪之后），是数学素养的定义逐渐明晰、内涵走向综合的阶段，“内容、过程和背景”成为揭示数学素养内涵的3条主线[18]．

2.2.1 国外学者对数学素养内涵的界定

国外与数学素养的有关的术语主要有：Numerate、Numeracy（数字计算）、Literacy（知能：读、写、算）、Quantitative Literacy（数量方面的知识能力）、Mathematical Literacy（或Matheracy，数学知识能力）．对于“数学素养”的解释，不同时期有所不同，即使在同一时期，不同国家、组织机构，不同学者的理解也是不同的，目前尚无统一明确的定义．表2仅列举出部分较具代表性的定义．

表2 国外对数学素养内涵的代表性描述

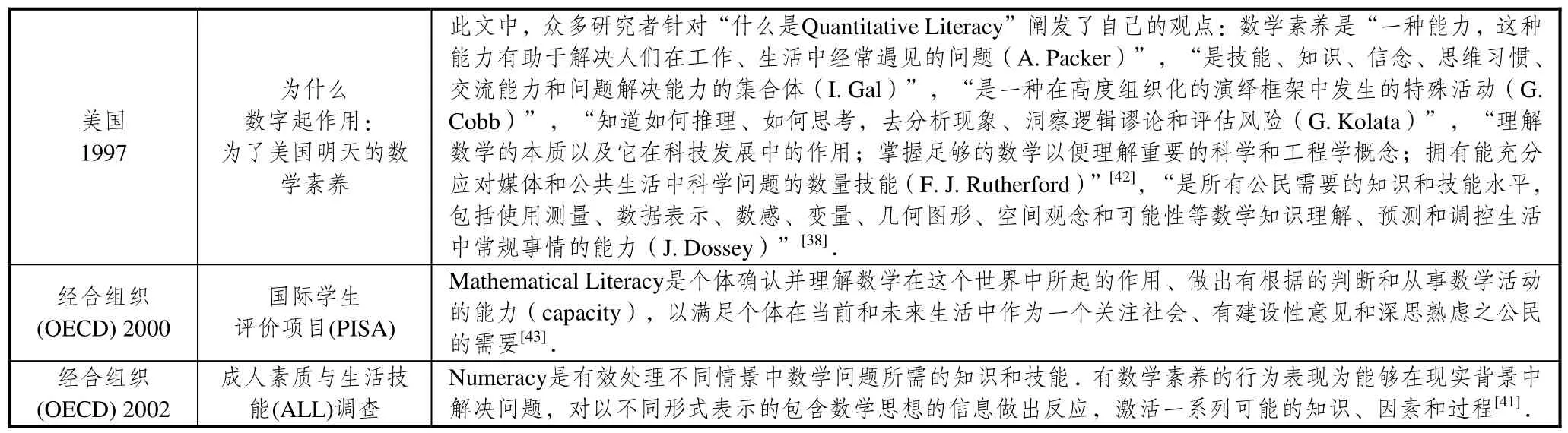
表2 （续） 国外对数学素养内涵的代表性描述

2.2.2 国外的数学素养观分类

概括而言，国外的数学素养观主要分4种类型：

（1）“背景需要”取向的数学素养观．

“背景需要”取向的数学素养观，是从家庭、工作、社会等特定区域情境对数学的需要来界定数学素养．这类研究强调，没有真实的情境需要，数学素养就无法外显、无法判断，因而“背景”会成为定义的重要组成部分．

澳大利亚数学教师协会指出，“数学素养就是能有效地应用数学来满足家庭生活、工作的需要，满足参与社区和公民生活的需要．”[38]

1992年，新西兰教育研究委员会认为一个人像在课堂中一样，在现实生活中能拥有运用数学的自信和技能，就称为有数学素养的（Numerate）[38]．

I. Gal认为：“数学素养是技能、知识、信念、态度、思维习惯以及一般交流、问题解决能力的集合体，这是人们有效应对真实世界情境或含有数学、可计量元素的任务所必需的．”[44]

（2）“数学知识”取向的数学素养观．

“数学知识”取向的数学素养观，强调数学知识对于成为有数学素养的人来说是非常重要的．数学知识包括了数、测量、代数、几何以及统计等领域．当然，不同的定义涉及的数学知识有差异．

John A. Paulos认为，数学素养是更好地理解个人情境中的有关数量[45]．

Jesse L. M. Wilkins 认为：“数学素养是对代数和几何的全面理解．”[46]

（3）“数学过程”取向的数学素养观．

“数学过程”取向的数学素养观聚焦于问题解决、逻辑推理、数学交流、数学表达、数学运用、数学观念、数学欣赏等各种数学过程，将能力和态度视为数学素养的核心内容．当然，这一类中的各种观点的侧重点有所不同．有的关注数学方法的理解和欣赏，有的重视数学态度和价值观；有的强调基本技能（如算术运算），有的强调高水平思维能力和使用数量工具的能力．表2中的很多描述属于这一类．

（4）“多维度”取向的数学素养观．

“多维度”取向的数学素养观，将“背景需要”、“数学知识”与“数学过程”3个因素综合起来界定数学素养．为了使数学素养的定义变得明晰，PISA项目中数学素养设计主席Jan De Lange给出了一些解释性的评论[47]：

用“素养”这一术语，我们是想强调那些在数学课程背景中已经被定义和可以定义的数学知识和技能不构成我们测评的核心内容．相反，我们所想的是以各式各样、沉思的、基于洞察力的方式把数学知识放入大量背景的功能性运用中．

数学素养不能够被简化成数学术语、事实、程序以及完成某些运算、执行某些方法的各种技能等等知识．我们想强调“素养”这一术语不被限定在指示基本的、最低水平的功能性．相反，我们认为素养是一个连续的、多维的光谱（spectrum），从基本的功能性变化到高水平的技能知识掌握．

暗含在我们的数学素养概念中至关重要的能力是提出、表达和解决各种领域和环境中的数学问题．这些问题的范围从纯数学的到开始没有呈现出、但能够被问题提出者或解决者成功抽取出数学结构的问题．

态度和情感（如，自信心，好奇心，兴趣，做事和理解事情的期望）不包括在数学素养定义的组成成分中．然而，它们是数学素养的重要的先决条件．原则上，没有这些态度和情感也有可能拥有数学素养．然而实际上，一个人没有一定程度的自信心、好奇心、兴趣和期望做或理解包含数学成分的事情，是不可能发挥素养并应用在实际之中的．

综上，PISA项目形成了比较综合的定义：数学素养（Mathematical Literacy）是个体确认并理解数学在这个世界中所起的作用、做出有根据的判断和从事数学活动的能力（capacity），以满足个体在当前和未来生活中作为一个关注社会、有建设性意见和深思熟虑之公民的需要．

定义中的“这个世界”是指个体生活所在的自然、社会和文化环境；“从事数学活动”不是狭义的从事物理或社会活动，而是还包括数学交流、立场、评价和欣赏数学知识，不能仅局限于数学的功能性用途，而应体现数学的美学价值；“当前和未来生活”囊括个体的私人生活、职业生活、社会生活以及公民生活．

PISA不仅关注数学内容的掌握，还特别注重应用数学的过程，因而数学情境就是一个非常重要的方面，将数学与现实、静态与动态结合在一起．由此可见，“多维度”取向的数学素养观，将数学素养看作在现实情境中发挥功用的数学知识、数学能力与数学情感的统一体．

3 数学素养的内涵界定与构成要素研究

3.1 素养的本质

素养与素质密切相关．对“素质”这一术语的解释有很多观点，研究者比较认同这一观点：素质是指人的先天遗传特质和后天形成的能力，包括修养、精神、气质、审美、爱好、志趣、习惯、思维、知识技能、实践能力、生存能力等．（黄书光，2006）[48]

阳凌云（2005）认为，现代素质观有3个共同点：一是素质包括先天和后天两方面的素质；二是素质的形成和发展受环境和教育的影响；三是强调了素质形成过程中的“内化”机制[49]．

素质教育是根据人的发展和社会发展的实际需要，以全面提高全体学生的基本素质为根本目的，以尊重学生个性，注重开发人的身心潜能，注重形成人的健全个性为根本特征的教育．为此，2011年，中华人民共和国教育部从培养目标、课程与教学以及家庭、学校、社会3个角度提出了30条素质教育理念[50]．

素养不同于素质，素质含有先天遗传特质的成分，而素养主要是靠后天的学习实践活动形成的．也就是说，素质中有些东西是不可教的，也不可学的，而素养是可以培养的．

素养（competencies）不只是“知识（know ledge）”或“技能（skill）”或“能力（ability、capacity）”，也不是“知识+能力”，“知识+能力”就是“知能（literacy）”．知能最初的含义主要是指学科的一些能力，比如说听、说、读、写方面的知识能力．PISA测试主要是测试学生在语言、数学、科学等学科方面的能力．而素养比知能的意义更为广泛，它不但含有知识和能力，还包括了情感态度价值观．当然，现在的PISA测试已将“知能（literacy）”的意义拓展到了“素养（competencies）”．

研究者认为，素养是学生为了满足个人发展和社会发展所必需的、重要的、关键的知识、能力和情感态度价值观．素养是可以培养的，它是一个有阶段性的动态发展系统．

3.2 对“多维度”取向的数学素养观的反思

由国内外数学素养研究的梳理部分可知，从历史演变的角度，国内的数学素养观的发展历程为：

国外的数学素养观的发展历程为：

当今，不管是国内还是国外，人们对“多维度”取向的数学素养观已经达成共识，数学素养包括了数学知识、数学能力和数学情感态度价值观．

把数学知识、数学能力、数学情感态度价值观作为数学素养的3大构成要素，是数学素养研究的一大进步，但这一要素结构存在着以下3个问题．

第一，这个三要素结构比较粗，不好具体区分落实，从而导致知识当能力、能力技巧化、有知识和能力但缺少深刻理解和良好态度的素养缺失教育．

第二，素养不是简单的知识+技能+能力+情感态度的加法结果．

（1）知识与技能联系紧密，数学认知技能需要知识的理解和思想的引领．

何小亚（2011）指出，在中国，人们长期以来把数学知识表述为数学中的概念、法则、性质、公式、公理、定理．技能是按照一定的程序或步骤进行的一种机械性操作．人们经常说，学校教育既要传授知识，也要形成技能．在教学实践中，数学知识的教学较多地演变为知识的言语信息的记忆和机械的模仿操作．而技能则更多地被理解为动作操作，忽略了心智技能．

知识（传统意义上的）与技能有着密切的联系，技能在知识的学习过程中逐步形成和得到发展，反之，一定的技能是知识的学习的必要条件．因此，不应该将知识与技能割裂开．实际上，与现代认知心理学相比，传统意义上的知识和技能分别对应着陈述性知识和程序性知识．

陈述性知识是关于事实的，能直接陈述的知识，它主要用于回答“是什么”的问题，它实际上是一系列的言语信息，主要以命题和命题网络的形式表征．程序性知识是关于操作的产生式系统，它主要用于回答“会做什么”的问题．程序性知识分为智慧技能和认知策略，以产生式系统表征．

皮连生先生认为，技能分为动作技能和认知技能，动作技能是在练习基础上形成的按某种规则或操作程序顺利完成身体协调任务的能力，而认知技能是在练习基础上形成的按某种规则或操作程序顺利完成智慧任务的能力，它包括了智慧技能和认知策略[51]．数学智慧技能的习得和保持需要知识的理解，而认知策略则需要数学思想的引领．

（2）意会知识涉及到了情感体验．

英国哲学家M. Planyi认为，人类大脑中的知识分为明确知识（explidt know ledge）和意会知识（tacit know ledge）．明确知识是指能言传的，可以用文字来表述的知识．意会知识是指不能言传的，不能系统表述的知识．意会知识是镶嵌于实践活动之中的，是情境性的和个体化的，只可意会，不可言传．传统的数学学习方式只注意到了数学明确知识的学习，忽视了数学的意识、思想和态度等数学意会知识的学习．意会知识隐藏在人类的实践活动中，只有通过亲身的活动体验才能学会和提高[51]．

第三，“数学知识”与“数学能力”不宜作为数学素养的一级指标．

从教学实践的操作性和教育评价的可测量这两个角度考虑，较抽象、较复杂和易混淆的“数学知识”与“数学能力”不宜作为数学素养的一级指标．而数学运算、数学推理、数学意识、数学思想方法和数学情感态度价值观这5个要素则比较符合共同性、操作性和可测量的要求．

算术中有数值计算，代数中有代数运算，而几何、统计与概率也离不开这两种运算．

代数中需要数学推理，几何离不开数学推理，统计与概率需要数学推理，问题解决更需要数学推理．

算术需要数的意识、代数需要符号意识、几何需要空间观念、统计与概率需要数据分析意识、问题解决中需要应用意识．

数学思想方法是数学中重要的内容，其中的数学思想是数学的灵魂，它们贯穿与各个数学领域之中．数学思想灵魂的缺失是过去数学教育的一大失败．

数学情感态度价值观是各个数学领域的学习中都共有的，它属于内隐的心理结构，不是明确知识，而是意会知识，无法通过传授而直接获得，必须通过学生的过程性学习间接获得．它是教师以知识技能为基础，以过程方法为途径，在引导学生学习数学的过程中形成的[52]．

不可否认，数学情感态度价值观的内容及测量是最困难的．数学情感态度价值观的界定及内容分类将在3.3和4.1小节中介绍．其测量也有了文献[53]的研究作为基础．

3.3 数学素养的内涵及构成要素

基于上述国内外数学素养研究成果的分析、梳理和筛选，将学生数学素养的内涵界定为：数学素养是指学生为了满足自身发展和社会发展所必备的数学方面的品格和能力，是数学的知识、能力和情感态度价值观的综合体．

选择数学素养构成要素的5个标准：一是反映数学的学科特色；二是在数学较多领域中共有；三是可以培养；四是容易分学段阐述；五是可以测量．根据这一标准，确定数学素养的构成要素为：数学运算、数学推理、数学意识、数学思想方法和数学情感态度价值观．

数学运算是指，根据算理和算法对数与式进行的运算．它要求运算要正确、迅速、合理，并对运算结果的正确性进行判断、验算．它包括：◆数值计算 ◆代数运算．

数学推理是指，由一个或几个已知判断得出一个新的数学判断的思维形式．它包括：

◆演绎推理：从已有的事实（包括定义、公理、定理等）和确定的规则（包括运算的定义、法则、顺序等）出发，按照推理规则进行的推理．其形式既有形式逻辑方面的分析、综合、抽象、概括、比较、分类、完全归纳、演绎、系统化、证明、反驳，也有辩证逻辑方面的已知与未知的互化、直与曲的互化、有限与无限的互化、化陌生为熟悉、化繁为简、正难则反、顺推与逆推之结合、动与静之转化、一般与特殊之转化，等等．

◆合情推理：从已有的事实出发，凭借经验和直觉，通过不完全归纳、类比和想象等方式来推断某些结果的推理．

数学意识是个体在思考问题时在数学方面的自觉意识或思维习惯．它包括：

◆数的意识：对数的意义的理解；数的表示；数的大小的相对性；用数进行交流；算法的选择；数值的估算与解释．

◆符号意识：能够理解并且运用符号表示数、数量关系和变化规律；知道使用符号可以进行运算和推理，所得到的结论具有一般性，能用符号进行交流．

◆空间观念：指根据物体特征抽象出几何图形，根据几何图形想象出所描述的实际物体；想象出物体的方位和相互之间的位置关系；描述图形的运动和变化；依据语言的描述画出图形，图形的分解与组合，等等．

◆数据分析意识：意识到数据中隐藏着重要信息；有收集数据、分析数据、用数据说理的习惯；意识到数据分析方法的多样性与合理性；通过数据分析体验随机性．

◆应用意识：有两个方面的含义，一方面有意识利用数学的概念、原理和方法解释现实世界中的现象，解决现实世界中的问题；另一方面，认识到现实生活中蕴涵着大量与数量和图形有关的问题，这些问题可以抽象成数学问题，用数学的方法予以解决．

数学思想方法是数学思想和数学方法的统一，它既含有观念层面的数学思想又含有操作层面的数学方法．它包括：数学表示、数形结合、公理化、化归、RM I原则、数学建模、统计思想、随机思想、微积分思想，等等．

数学情感态度价值观是指，个体对数学学科、数学活动、数学对象的喜好、立场观念等．

心理倾向．它包括：对数学有自信心，认识到数学的科学价值、应用价值和文化价值，能感受数学的精确性、抽象性、概括性、应用性、简洁性、整齐性、对称性、和谐性、统一性等独特之美，等等．

4 数学素养的层次与行为表现

4.1 数学素养的层次

按照学生获得的先后顺序和难易程度，数学素养的表现水平可以由低到高分成3个层次：数学知识与技能、数学过程与方法和数学情感态度价值观[52]．

4.1.1 数学知识与技能

这一层次指的是数学基础知识和基本技能．其内容主要包括3类：一类是数学概念、数学原理（即数学定理、性质、公式、法则）、基本的数学事实结论这样一些用于回答“是什么”问题的陈述性知识，它属于言语信息；第二类是涉及到数学概念、数学原理、基本的数学事实结论的运用，用于回答“做什么”的问题的程序性知识，它属于认知技能；第三类是数学操作性技能，它属于动作技能．

知识与技能层次的要求还可以分成以下4个层次：

了解：能回忆出知识的言语信息；能辨认出知识 的常见例证；会举例说明知识的相关属性．

理解：能把握知识的本质属性；能与相关知识建立联系；能区别知识的例证与反例．

掌握：在理解的基础上，能直接把知识运用于新的情境．综合运用：能综合运用知识解决问题．

4.1.2 数学过程与方法

过程与方法的内容是：通过数学学习过程，把握数学思想方法，形成数学能力，发展数学思维、数学意识和创新意识，提高问题解决能力，积累数学活动经验．

4.1.3 数学情感态度价值观

这里的情感是指在数学活动过程中比较稳定的情绪体验．数学态度是指对数学活动、数学对象的心理倾向或立场，表现出兴趣、爱好、喜欢与否、看法立场．数学态度可以演变为数学信念——对数学持有的较为稳定的总体看法、观念．数学态度包括对数学学科的态度（即数学信念）、对数学的兴趣、对数学具体内容的态度．这一层次的内容还包括宏观的价值观和数学审美观．

4.2 数学素养的行为表现

以数学素养提高为目的的数学教育，要求学生理解基本的数学概念和原理，具备一定的运算、抽象、推理能力，能运用数学解决问题，会用数学语言来表达和交流，形成良好的数学情感态度价值观．

5 数学素养的要求领域分类模型

根据数学素养的定义与构成要素，无论是在小学、初中阶段，还是在高中阶段，学生的数学素养要求领域分类可以统一为如表3所示的模型．

表3 数学素养要求分类模型

[1] 中华人民共和国教育部．义务教育数学课程标准（2011年版）[M]．北京：北京师范大学出版社，2012．

[2] 中华人民共和国教育部．普通高中数学课程标准（实验）[M]．北京：人民教育出版社，2003．

[3] 数学课程标准研制组．全日制义务教育数学课程标准（实验稿）解读[M]．北京：北京师范大学出版社，2002．

[4] 数学课程标准研制组．普通高中数学课程标准（实验）解读[M]．南京：江苏教育出版社，2004．

[5] 康世刚．数学素养生成的教学研究[D]．西南大学，2009．

[6] 江苏省连云港市教科所“MA”课题组．“发展学生数学思想，提高学生数学素养”教学实验研究报告[J]．课程·教材·教法，1997，（8）：35-39．

[7] 张建良．“高中数学新课标”对数学教师的数学素养提出了高要求[J]．数学教育学报，2005，14（3）：87-89．

[8] 王子兴．论数学素养[J]．数学通报，2002，（1）：6-9．

[9] 谢恩泽，滕福星，徐本顺，等．文科学生的自然科学素养[M]．济南：山东教育出版社，1991．

[10] 郑强．数学素养与数学教学[J]．山东教育学院学报，2006，（5）：1-3．

[11] 束仁武．充分利用“想一想”培养学生的数学素养[J]．中学数学，1997，（11）：10-12．

[12] 刘俊先．论数学史对提高数学素养的重要作用[J]．教育与职业，2009，（24）：175-176．

[13] 苏洪雨，江雪萍，桂鹏．基于几何问题情境的高中教师的数学素养研究[J]．数学教育报，2010，19（1）：81-84．

[14] 朱德江．小学生数学素养的构成要素与培养策略[J]．学科教育，2004，（7）：27-31．

[15] 姚丽行．提高学生数学素养的几点思考[J]．基础教育研究，1995，（1）：20-21．

[16] 张奠宙．数学教育研究导引[M]．南京：江苏教育出版社，1994．

[17] 潘小明．关于数学素养及其培养的若干认识[J]．数学教育学报，2009，18（5）：23-27．

[18] 刘喆．论师范生数学素养[D]．华南师范大学，2011．

[19] 蔡上鹤．民族素质和数学素养——学习《中国教育改革和发展纲要》的一点体会[J]．课程·教材·教法，1994，（2）：15-17．

[20] 江西省教委教研室“提高数学素养”课题组．提高数学素养的思考[J]．数学通报，1995，（5）：22-24．

[21] 车翔玖．论高师院校数学专业学生科学的数学素养[J]．吉林师范学院学报，1996，（5）：23-25．

[22] 戚绍斌．试论高校数学师范生数学素养的内涵与结构[J]．梧州师专学报，1996，（2）：23-28．

[23] 李树臣．加强数学观念教育 提高国民数学素养[J]．山东教育科研，1998，（3）：28-30．

[24] 顾沛．十种数学能力和五种数学素养[J]．高等数学研究，2000，（11）：5．

[25] 孔企平．西方数学教育中“Numeracy”理论初探[J]．全球教育展望，2001，（4）：56-59．

[26] 朱德全．数学素养构成要素探析[J]．中国教育学刊，2002，（5）：49-51．

[27] 王岳姝．中等职业学校学生数学素养培养若干问题研究[D]．天津大学，2003．

[28] 彭玉忠．师范生的数学素养及其提高策略[J]．师范教育，2003，（11）：5-6．

[29] 郑强．论数学课程标准中的数学素养观[J]．山东教育学院学报，2005，（5）：1-17．

[30] 张亚静．数学素养：学生的一种重要素质—基于数学文化价值的思考[J]．中国教育学刊，2006，（3）：65-67．

[31] 段志贵．高师数学专业学生数学素养的构成及其培养[A]．全国高师会数学教育研究会2006年学术年会论文集，2006．

[32] 桂德怀，徐斌艳．数学素养内涵之探析[J]．数学教育学报，2008，17，（5）：22-24．

[33] 吴晓红．地方师范院校文科大学生数学素养的现状及提高[J]．数学教育学报，2011，20（2）：49-52．

[34] 苏洪雨．学生几何素养的内涵与评价研究[D]．华东师范大学，2009．

[35] 桂德怀．中学生代数素养内涵与评价研究[D]．华东师范大学，2011．

[36] 徐德均．“百年通中”教育发展之启迪——从三位数学院士的成长片段看数学素养教育[J]．数学教育学报，2011，20（5）：86-89．

[37] O’ Donoghue J. Numeracy and Mathematics [J]. Irish Math, 2002, (48): 47-55．

[38] Neil W A lex. The Essentials of Numeracy. Paper Prepare for New Zealand Association of Research in Education Conference [EB/OL]. http://www.nzcer.org.nz/pdfs/10604.pdf.

[39] 陈昌平．数学教育比较与研究[M]．上海：华东师范大学出版社，2000．

[40] National Council of Teachers of Mathematics (NCTM) (1989). Curriculum and Evaluation Standards for School Mathematics [EB/OL]. http://www.standards.nctm.org/documents.

[41] Gal I, Manly M, M ieke van Groenestijn. Adult Numeracy and Its Assessment in The All Survey: A Conceptual Framework and Pilot Result s [M]. Ottawa: Statistics Canada, 2002.

[42] Steen L A. Reading, W riting, and Numeracy [J]. Liberal Education, 2000, (86): 26-36.

[43] OECD. Learning for Tomorrow’s World. First Results from PISA2003 [EB/OL]. http://www. pisa.oecd.org/pages/.

[44] Gal I. Big picture: What does “Numeracy” Mean [EB/OL]. http://forum.swarth.more.edu/teachers/adult.ed/articals/gal. htm l.

[45] Eva Jablonka. Mathematieal Literacy [A]. In: Alan J Bishop. Second International Mathemarics Education [C]. Kluwer Academ ic Publisher, 2003.

[46] Jesse L M Wilkins. Preparing for the 21st Century: The Status of Quantitative Literacy in the United States [J]. School Science and Mathematics, 2000, 100(8): 405-418.

[47] Jan de Lange. Mathematical Literacy for Living from OECD-PISA Perspective [J]. Tsukuba Journal of Educational Study in Mathematics, 2006, (25): 13-35.

[48] 黄书光．中国基础教育改革的历史反思与前瞻[M]．天津：天津教育出版社，2006．

[49] 阳凌云．数学素质教育导论[M]．长沙：湖南科学技术出版社，2005．

[50] 中华人民共和国教育部．素质教育学习提要[M]．北京：生活·读书·新知三联书店出版社，2001．

[51] 何小亚．数学学与教的心理学[M]．广州：华南理工大学出版社，2011．

[52] 何小亚．中学数学教学设计（第二版）．北京：科学出版社，2012．

[53] 何小亚，李耀光．初中生数学态度量表的编制及信度效度检验[J]．数学教育学报，2013，22（2）：37-43．

Theoretical Analysis of the Students’ M athematical Com petence’ Indicators

HE Xiao-ya
(School of Mathematical Sciences, South China Normal University, Guangdong Guangzhou 510631, China)

Mathematical competence concept in the domestic and overseas is divided into three types of “know ledge” orientation,“know ledge + ability” orientation and “multi-dimension” orientation; The mathematical competence of “multi-dimension”orientation exists three defects; Mathematical competence refers to the personality and capability on the aspect of math necessarily required to meet the self-development of students and social development, it is the combination of mathematical know ledge and ability as well as emotional attitude values, whose composing factors include mathematical operation, deduction, consciousness, ideological methods and emotional attitude values; Mathematical competence can be divided three levels from low to high, which are mathematical know ledge and skills, processes and methods of mathematics and mathematics emotional attitudes and values ;Behavioral expression of mathematical competence is that one understands basic mathematical concepts and principles, has certain operation and abstract and inferential capabilities, can use mathematics to solve problems, can use mathematical linguistics to express and communicate, and forms good mathematical emotion, attitude and value.

mathematical competence; connotation; constituent elements

G40-03

：A

：1004–9894（2015）01–0013–08

[责任编校：周学智]

2014–10–06

教育部哲学社会科学研究重大委托项目——我国高中阶段学生核心素养的模型及指标体系研究（13JZDW 009）

何小亚（1964—），男，贵州荔波人，教授，主要从事数学教学与数学学习心理研究．