基于自适应非趋势波动分析的齿轮振动信号特征提取

吴永恒， 肖 涵

(武汉科技大学 机械自动化学院 冶金装备及其控制教育部重点实验室,武汉 430081)

基于自适应非趋势波动分析的齿轮振动信号特征提取

吴永恒， 肖 涵

(武汉科技大学 机械自动化学院 冶金装备及其控制教育部重点实验室,武汉 430081)

非趋势波动分析用于齿轮故障识别时常采用标度指数作为特征量，该特征量容易导致齿轮故障模式间存在混叠。根据对数尺度波动函数图，将标度指数与表征信号强度的截距组成齿轮振动信号的特征向量。根据齿轮振动信号的双标度性，提出滑动加窗算法，实现标度指数的自适应提取，并结合神经网络算法进行故障分类。设计单级齿轮减速器的实验平台，并采集齿轮的径向振动信号进行自适应非趋势波动分析，研究表明，该方法能够提高标度指数的提取精度和提取效率。

非趋势波动分析；标度指数；长程相关性；聚类；神经网络

齿轮广泛应用于各种机械设备中，由齿轮故障引起机械设备无法正常工作的现象层出不穷，特别是对于一些大型连续生产设备，如轧钢设备，一旦故障，将会造成极大的经济损失。目前，对齿轮的状态监测主要是基于齿轮的振动信号进行的，而所采取的振动信号含有大量的与齿轮运动无关的信号，使得齿轮振动信号呈现非平稳性。传统的频谱分析、时域统计方法都是在假设信号是平稳的前提下进行的。因此传统方法不能完全提取信号所含有的信息。一些非平稳信号的处理方法如：时频分析、小波变换及小波变换的变种、多分辨奇异值分解、经验模式分解(Empirical Mode Decomposition, EMD)[1-3]等方法虽然改进了传统方法的不足，但它们比较依赖故障所产生的特征频率成分，如果故障特征的频率成分较弱或被其它信号成分所盖，这些非平稳信号处理方法也就很难取得有效的成果。

非趋势波动分析(Detrended Fluctuation Analysis，DFA)是由Peng等[4]根据DNA机理提出的标度指数计算方法，主要用于分析时间序列的长程相关性。其优点在于可以有效的滤除序列中各阶趋势成分，能检测含有噪声且叠加有多项式趋势信号的长程相关，这种长程相关性反映了时间序列内部动力学机制，因此可以根据标度指数来描述设备的状态信息，适合非平稳时间序列的幂律相关分析。近年来，非趋势波动分析在金融、电子信号、气象[5-6]领域应用广泛。该方法同样可应用于齿轮故障特征量的提取。非趋势波动分析方法提取齿轮故障特征时，可将标度指数表征齿轮的故障状态并进行故障分类[7-8]，该方法的缺陷在于：没有考虑因时间尺度变化，信号所表现再来的多分形特征。研究表明，齿轮信号进行非趋势波动分析运算后得到的波动函数图具有双标度特性[9]，如图1所示，LogF(s)与Log(s)呈线性关系，其斜率便是标度指数α，可由最小二乘法拟合得到。双标度指数表明信号在不同尺度下存在着自相似性，信号存在分形特征。

图1 齿轮信号进行DFA运算后的双对数图Fig.1 Gear after the operation signal DFA double logarithmic graph

但是，应用传统DFA方法提取双对数图中的双标度指数时，最关键的问题在于，如何界定第一标度与第二标度的转折点，也就是图1中的转折点。转折点所对应的时间尺度往往需人工确定，其准确性直接影响双标度指数的精度和可靠性，所得到的结果因主观因素的影响，最终导致齿轮故障聚类时存在误差。为此，提出基于非趋势波动分析的双标度时间尺度转折点自适应提取方法。

1 自适应非趋势波动分析算法步骤

设有一个长度为N时间序列x(t),(t=1,2,3,…,N)，运用自适应DFA方法提取标度指数步骤如下：

(1) 对时间序列x(t)采用DFA运算，求出波动函数F(s)与窗口大小s变化曲线。假定时间序列x(t)长程幂律相关，则F(s)与s满足如下关系：F(s)～sα

对上式两端同时取对数得： Log[F(s)]～Log(s)

令Fqs(i)=Log[F(s)]

(2) 将序列Fqs(i)在i=m处分为左右两个窗口，如图(2)所示。采用最小二乘法分别对左右两个窗口进行一阶线性拟合。得到左右两边的拟合直线方程yz(x)和yy(x)。

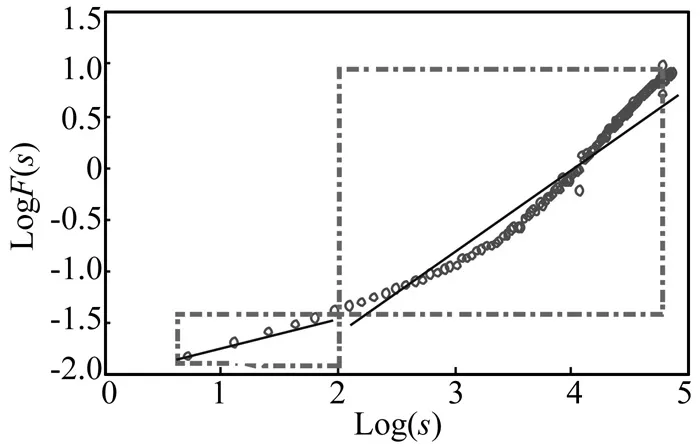
图2 齿轮信号进行DFA运算后的双对数图Fig.2 Gear after the operation signal DFA double logarithmic graph

(4) 按一定的步长增加左边的窗口，重复(2)～(3)，得出所有的Δ值，记为{Δi}。找出Δ值最小时的位置，并逆运算到双对数图中，找到转折点的实际位置M。

(5) 采用最小二乘法对转折点M左右两边分别进行一阶线性拟合，所得斜率为双标度指数，分别记为αz和αy。

2 实验装置与参数

由于齿轮在运转过程中，自身轮齿面刚度的周期变化和轮齿面的局部周期性接触，从而引起齿轮的径向振动与轴向振动，其中齿轮径向振动对轴承和齿轮箱的影响最大，构成噪声能量的主要部分，能够全面包含齿轮的状态信息。因此在实验过程中的测点主要分布在齿轮的径向方向，采集齿轮的径向振动。

实验数据采自齿轮故障实验台，为验证算法的有效性，齿轮故障皆为人为故障。实验台的结构简图以及各构件的参数如图3所示，由于齿轮径向振动对轴承的影响最大，因此振动加速度传感器安装在输入端轴承座的垂直端。分别采集齿轮正常、断齿、磨损、和周节误差四种常见故障的振动信号，各10组。

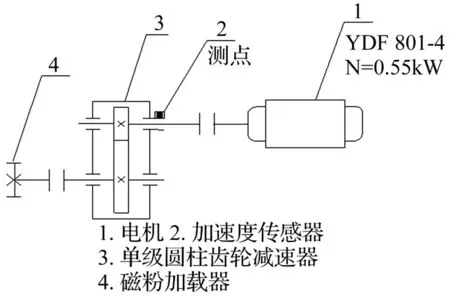
齿数电机转速负载采样时间采样频率Z1=20，Z2=37985r/min20N·m2s2048Hz

3 实验数据分析结果

四种模式下的自适应DFA所对应的Log[F(s)]-Log(s)曲线如图4(b)所示，(a)为四种模式下的振动信号图(只列出正常齿轮情况下的分析结果)。

图4 齿轮振动信号与相对应的双对数图Fig.4 Gear vibration signal with the corresponding double logarithmic graph

从图4可以看出，四种模式下经过自适应DFA运算后，所得到的Log[F(s)-Log(s)]曲线图具有两种线性关系，也就是前面所述的双标度特性。本实验对10组齿轮振动信号进行自适应DFA运算，所得到的双标度指数α1,α2如表1所示，均值和方差如表2所示。

从表1、2可以看出，四种齿轮箱振动信号的双标度指数的均方差都比较小，这说明这两个参量具有稳定性，能够准确地刻画时间序列内部的动力学行为，可以作为表征齿轮故障状态的特征参数。一些文献中将双标度指数联合起来，建立二维特征向量矩阵[α1,α2]来进行分类，效果都一般。另外从图3中明显可以看出来，不同模式下的标度指数所对应的截距各不相同，其大小与信号强度分布规律相关，所以将标度指数与其对应的截距联合建立二维特征向量组[α1,b1]或者[α2,b2]，分类结果如图5、6所示。与第二标度相比，第一标度对四种模式的齿轮振动信号区分能力更强，特征向量的集中性更佳。

表1 四种模式下齿轮振动信号双标度指数计算结果

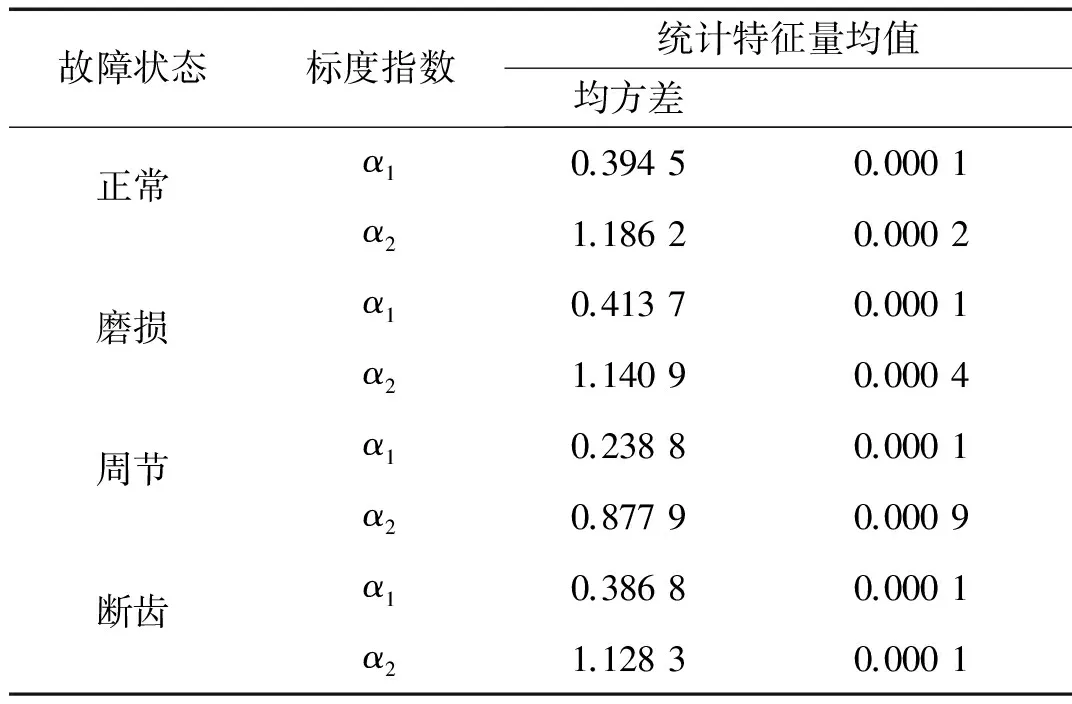
表2 四种模式下齿轮振动信号双标度指数的均值与方差

图5 单一标度与对应截距下齿轮故障分类效果Fig.5 Intercept corresponds to a single scale with the lower gear fault classification results

4 神经网络模型的故障识别(Probabilistic Neural Network PNN)

由于齿轮振动是一种非线性行为，所以需要一个对非线性分类能力极强的方法来进行故障模式识别。神经网络模型最大的优点是强大的非线性分类能力，将故障样本空间映射到故障模式空间中，从而形成一个具有较强纠错能力和结果自适应能力的故障诊断网络系统。本研究将采用PNN模型与自适应非趋势波动分析方法相结合，进行故障模式识别。具体步骤为：

(1) 采集数据；本文采用[α1,b1]作为特征向量组;

(2) 训练网络；选取来自于实验台的的20组数据作为训练样本，以1，2，3，4四类故障(断齿、正常、周节误差、磨损)为期望输出矢量。训练样本，得到PNN网络模型;

(3) 进行网络测试；训练完成后，输入80组数据进行检验，并对训练好的网络进行实际应用。

本文在实验台的基础上，定义训练样本20组，检验样本80组进行模式识别，所得结果见表3、4。

表3 自适应DFA模式识别结果

表4 一般DFA模式识别结果

从表3、4分类结果可以看出来，运用自适应方法对实验台的故障数据进行分类，80组数据只有断齿的分类出现1个误差，较之一般方法，提高了识别的准确率，可见自适应非趋势波动波动分析方法的实用性比较大，可靠性好。

5 结 论

针对齿轮振动信号非趋势波动分析的双标度性特征，提出双标度时间尺度转折点的自适应提取方法，克服了传统算法中存在的不精确性。实验表明，采用提出方法提取的双标度指数能减小故障分类误差，将第一标度指数与其对应的节距组成齿轮故障特征向量，并应用概率神经网络进行故障分类，取得了很好的故障识别率。但该方法采用数值分析方法得到的转折点还存在一定误差，可以借助假设检验的方法来进一步确认转折点的位置。

[1] 于德介,程军圣,杨宇. Hilbert-Huang 变换在齿轮故障诊断中的应用[J]. 机械工程学报,2005,41(6):102-107. YU De-jie, CHENG Jux-shen, YANG Yu. Hibert-Huang transform in gear fault diagnosise[J]. Chinese Journal of Mechanical Engineering，2005，41(6)：102-107.

[2] 陈向民,于德介,罗洁思. 基于线调频小波路径追踪阶比循环平稳解调的齿轮故障诊断[J]. 机械工程学报, 2012,48(3):95-101. CHEN Xiang-min,YU De-jie,LUO Jie-si. Gear tooth fault diagnosis by using order cyclostationary demodulatingapproach based on chirplet path pursuit[J]. Journal of Mechanical Engineering,2012,48(3):95-101.

[3] 吕勇,李友荣,徐金梧. 延时矢量方差算法及其在齿轮故障识别中的应用[J]. 振动与冲击,2006,25(6):59-61. LÜ LI You-rong,XU Jin-wu, Delay vector variance method and its application to gear fault diagnosis[J]. Journal of Vibration and Shock，2006,25(6):59-61.

[4] Peng C K, Buldyrev S V, Gold berger A L,et al. Finite size effects on long range correlations:Implications for analyzing DNA sequences[J].Physical Review E,1994,47(5):3730-3733.

[5] 张淑清,翟欣沛,刘永富,等,滑动去趋势波动分析在电能质量暂态扰动检测中的应用[J].电力系统自动化,2012.30(8):52-57. ZHANG Shu-qing， ZHAI Xin-pei， LIU Yong-fu，et al.Application of sliding detrended fluctuation analysis in detection of transient power quality disturbances[J].Automation of Electric Power Systems,2012,30(8):52-57.

[6] Echeverria J C, Alvarez-Ramirez J, Pean M A, et al. Fractal and nonlinear changes in the long-term baseline fluctuations of fetal heart rate[J].Med Eng Phys,34(4):466-47.

[7] 李力,彭中笑,彭书志. 去趋势波动分析在齿轮故障诊断中的应用研究[J]. 中国机械工程,2009,20(19): 2311-2314. LI Li,PENG Zhong-xiao,PENG Shu-zhi. Detrended fluctuation analysis for gear fault diagnosis[J].China Mechanical Engineering,2009,20(19):2311-2314.

[8] 何文平. 动力学结构突变检测方法的研究及其应用[D].兰州:兰州大学,2008.

[9] 林近山,陈前.基于非平稳时间序列双标度指数特征的齿轮箱故障诊断[J].机械工程学报,2012,43(13):108-114. LIN Jin-shan,CHEN Qian, Fault diagnosis of gearboxes based on the double-scaling-exponent characteristic of nonstationary time series[J]. Journal of Mechanical Engineering,2012,43(13):108-114.

[10] 夏志明,郭鹏江,赵文芝,等.Ⅳ模型中变点检测的 Cramer-VonMises方法[J].西北大学学报,2010,40(1):6-8. XIA Zhin-ming,GUO Peng-jiang,ZHAO Wen-zhi.Cramer-von misesmethod in detecting change points in IV models[J].Journal of Northwest University, 2010,40(1):6-8.

[11] 郭建英,周源泉.可靠性增长突变点辨识与MIL-HDBK-189[J].方法与应用,1998,1:30-32. GUO Jian-ying,ZHOU Yuan-quan. Reliability growth mutations identified with MIL-HDBK-189[J]. Methods and Applications,1998,1:30-32.

Adaptive detrended fluctuation analysis as a feature extraction method for gear’s vibration signal

WU Yong-heng, XIAO Han

(The Ministry of Education Key Laboratory of Metallurgical Equipment and Its Control, College of Machinery and Automation, Wuhan University of Science and Technology, Wuhan 430081, China)

Scaling exponent is often used as a feature measure for gear fault identification in detrended fluctuation analysis (DFA), but it leads easily to the problem of aliasing among gear failure modes. According to a logarithmic scale wave function diagram, the scaling exponents and the intercept of characterization of signal intensity were combined to make up a feature vector of gear vibration signal. According to the dual scaling character of gear vibration signal, a sliding windowing algorithm was projected to extract adaptively the scaling exponent, and used for fault classification combining with the neural network algorithm. The results show that the method can improve the extraction accuracy and extraction efficiency of the scaling exponent.

DFA; scaling exponent; long-range correlation; clustering; neural network

国家自然科学基金青年基金资助项目(51105284);湖北省高校优秀中青年创新团队计划(T200905)资助

2013-12-16 修改稿收到日期：2014-05-10

吴永恒 男，硕士生，1986年生

肖涵 男，副教授，1979年生

TH133

A

10.13465/j.cnki.jvs.2015.09.028