闭合型裂纹时间反转损伤识别

张 望， 吴维亮， 肖 黎， 屈文忠

(武汉大学 工程力学系，武汉 430072)

闭合型裂纹时间反转损伤识别

张 望， 吴维亮， 肖 黎， 屈文忠

(武汉大学 工程力学系，武汉 430072)

由于超声波能穿透闭合型裂纹界面，采用传统的线性超声技术难以检测和定位闭合型裂纹损伤，基于非线性时间反转理论研究了闭合型裂纹损伤检测方法。通过金属铝板上黏贴的压电激励/传感阵列，进行了Lamb波检测螺栓模拟的闭合型裂纹实验。根据Lamb波时间反转原理，得到激励重构信号。通过计算激励信号和重构信号间的相关系数定义了损伤指数,开发了能定位闭合型裂纹的成像算法。实验结果表明非线性超声时间反转方法能够有效地识别非线性的闭合型裂纹。

闭合型裂纹；结构健康监测；损伤检测；非线性时间反转；压电阵列

金属结构普遍应用于机械、航空航天和民用基础设施中。疲劳产生的闭合型裂纹扩展往往导致金属结构破坏，造成重大损失。闭合型裂纹界面往往保持闭合接触，传统的线性超声技术难以检测到。只有当超声激励幅值超过某一阈值,裂纹界面开始部分张开与闭合，响应具有非线性特征。因此非线性超声成为闭合型裂纹潜在的识别手段[1]。

应用Lamb波时间反转理论与方法进行板类结构的损伤检测研究成果不断。该方法是利用Lamb波时间反转过程中的信号重构特性,将换能器接收到的信号进行时间反转后重新发射，将在信号源点处聚焦。Fink, Hoon, Xu与Giurgiutiu等[2-7]均进行了Lamb波时间反转的理论分析和实验工作。袁慎芳等[8]基于时间反转理论进行了复合材料螺栓连接失效损伤监测的实验。Park等[9]利用Lamb波时间反转特性进行了金属板损伤检测的实验，用钢块模拟了板上的线性损伤，详细分析了时间反转后的重构波形与原始波形的不同，从而判断出结构损伤的存在。但该实验中钢块模拟的是线性损伤,重构信号主波包的波形应接近于原始波形，实验结论值得进一步讨论。尽管有关Lamb波时间反转技术能有效检测某些类型损伤的实验研究不断,但是基于非线性超声的Lamb波时间反转方法进行闭合型裂纹的损伤识别与定位研究鲜见报道。

本文基于Lamb波时间反转理论，进行了闭合型裂纹的非线性超声损伤检测实验，利用Lamb波时间反转重构信号与原始激励信号构造了相关性损伤指数，识别并图像定位了金属铝板上的模拟闭合型裂纹损伤。

1 Lamb波时间反转理论

Lamb波在二维板中时间反转过程如图1所示。PZTA上施加一个激励信号(步骤1),激发出的Lamb波在板内传播一段距离后被PZTB接收(步骤2),接收到的信号在时域内经过时间反转处理 (步骤3)，重新施加到PZTB上再发射，PZTA记录的Lamb波信号即是原始激励信号经过时间反转后的重构信号 (步骤4)。

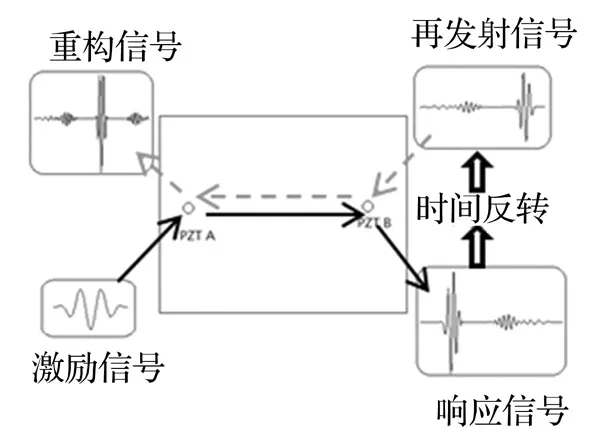
图1 Lamb波时间反转过程示意图Fig.1 A sketch map of the Lamb wave time reversal process

根据图1，中心频率为ω的正弦激励信号VA(ω)施加到PZTA上，激发出在板内传播的Lamb波。PZTA产生Lamb波的时域信号和能量分别为：

(1)

EA(ω)=kA(ω)VA(ω)

(2)

式中:kA(ω)为传感器A的压电系数。传感器B接收到的波信号可以写为：

VB(ω)=kB(ω)-1G(ω)kA(ω)VA(ω)

(3)

式中：G(ω)为板的传递函数，kB(ω)为传感器B的压电系数。当作动器和传感器使用相同的压电传感器时，即kB(ω)=kA(ω)，有：

VB(ω)=G(ω)VA(ω)

(4)

经过时间反转过程后，PZTA接收到的重构信号为：

V′A(ω)=G2(ω)VA(ω)

(5)

在时域内，重构信号可以写为:

(6)

理论上，如果在PZTA与PZTB之间的主动传感路径上不存在损伤时，时域内波信号V′A(t)与VA(t)相等；归一化后，重构信号V′A(t)的波形与原始激励信号VA(t)相同。

由于Lamb波的多模式特性，其时间反转过程变得复杂。图1中，选择特定频率的窄带信号施加到PZTA，激发出的Lamb波在板中传播只有S0和A0模式，该多模式信号被PZTB接收，经过时间反转重新施加到PZTB上再发射。A0和S0模式波在板上传播，分别产生与之对应的S0和A0模式波，因此最后得到含有4个波包的重构信号，叠加后的重构信号由中间的主波包和两侧的旁瓣波包构成[6]。由于线弹性系统波动的互易性[10-11]，Lamb波时间可逆性使得主波包波形与原始输入信号相同。

对于闭合型裂纹，当应力波幅值不足以张开裂纹界面时，闭合型裂纹在应力波的传播路径上表现为线性散射体，只有当应力波幅值超过某一阈值后,裂纹界面开始部分张开与闭合，成为波传播路径上的非线性源，此时响应具有非线性特征，波动的线性互易性和时间可逆性不再成立，Lamb波的中心频率发生改变。大幅值的波动激励信号与裂纹界面相互作用产生非线性成分，如高阶谐波与亚谐波，时间反转重构波形V′A(t)将不同于原始输入信号VA(t)。通过比较原始输入信号和重构信号间的差异，定义损伤指数DI(Damage Index)，可以识别出非线性类型的结构损伤(如金属结构中的疲劳裂纹和复合材料结构中的层脱等)。

2 损伤指数和损伤定位成像

定义损伤指数(DI)，是利用Lamb波传播的各条主动传感路径上的原始激励信号VA(t)={v1,v2,…,vn}和重构信号V′A(t)={v′1,v′2,…,v′n}间的相关系数定量描述两个信号之间的差异，为：

ρvi,v′i(t)=

(7)

式中:VA(t)和V′A(t)需要归一化后再进行相关性计算处理。ρvi,v′i(t)的值表示VA(t)和V′A(t)两个信号的相似度。两个信号相同时，ρvi,v′i(t)=1

损伤指数(DI)定义为：

DI=1-ρvi,v′i(t)

(8)

DI的值越大，损伤存在以及靠近Lamb波传播路径的可能性越高，是一个关于损伤到传感路径距离的分布函数，如下式：

(9)

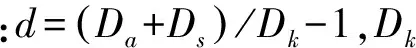
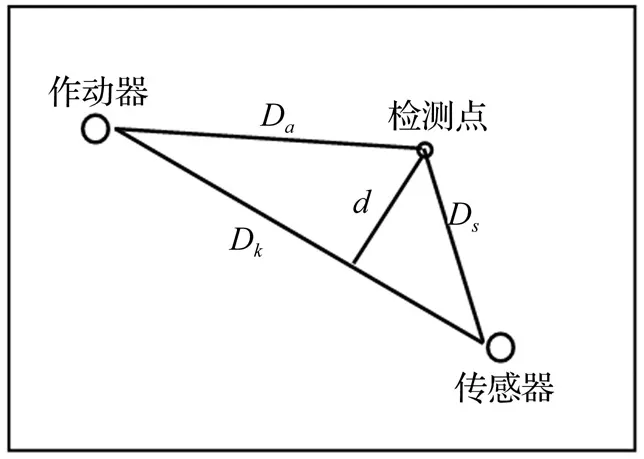
图2 传感路径示意图Fig.2 Illustration of senor path

设大面积损伤识别的主动传感网络存在n条传感路径，损伤位于点(x,y)的概率为：

(10)

式中:Pk(x,y)是损伤在点(x,y)的概率，DIk和fk(d)分别为式(8)定义的损伤指数和式(9)表示的损伤存在于第k条路径上的分布。

这种算法应用到每条传感路径上，可以得到板上各个位置即每个检测点的P(x,y)值。求和每条路径上对应点的P(x,y)值，最大P(x,y)值对应的检测点即为损伤存在的位置。用图像显示板上各点的P(x,y)值，即可定位损伤区域。

3 实验研究

3.1 实验装置

整体实验装置如图3所示。采用一个1 000 mm×1 000 mm×2 mm的铝板来评估本文中给出的方法。粘贴2列16个直径6.35 mm，厚0.25 mm的APC850压电陶瓷片组成压电作动/传感阵列，位置(1-16)如图4所示。一个直径15 mm，高 30 mm的圆柱形钢块黏贴于铝板(500, 500)mm处，模拟线性散射体。使用力矩扳手，用19 N·m的扭矩将一个砂纸打磨抛光过的螺栓固定在铝板上(380, 440)mm处，压电片在大幅值激励电压作用下产生的应力波与螺栓和铝板间非良好的接触面交互作用产生非线性响应，模拟非线性的闭合型裂纹。由Agilent 33522A任意函数发生器产生的激励信号，经Tegam 2350电压放大器放大后施加在作动器阵列上激发Lamb波，Agilent D50-X3014A示波器接收记录信号。板上压电阵列和损伤位置示意图如图4所示。

图3 实验装置Fig.3 Experimental setup

图4 板上压电阵列和损伤的位置示意图(mm)Fig.4 Schematic diagram of the PZT array and damage position

图5 Hanning窗调制3.5周期正弦激励信号Fig.5 3.5 counts 100 kHz Hanning window modulated sine tone burst

图6 路径7-16Lamb波时间反转过程Fig.6 Experimental waves in Lamb wave time reversal procedure for the path P7-16

当压电片的激励电压较小时，应力波幅值不足以张开闭合型裂纹的2个界面，闭合型裂纹在应力波的传播路径上表现为线性散射体；增大激励电压直至超过某一阈值，闭合型裂纹界面开始张开与闭合，2个界面接触作用产生非线性响应。根据该特性，本文实验的具体步骤如下：激励信号为3.5周期中心频率为100 kHz Hanning窗调制窄带正弦信号，如图5 所示。第一步，选择峰-峰值为50 V较小的激励电压依次激励作动器(#1-#8)，8个接收传感器(#9-#16)同时记录信号。选择合适的时间窗口对记录信号进行时间反转，同时消除了板边界反射的影响。重新施加到对应的接收传感器再发射。为消除各信号由于传播路径不同引起的信号衰减差异，将时间反转后的信号进行了归一化处理。压电作动器阵列用来接收时间反转传播的Lamb波信号。第二步, 选择150 V峰-峰值较大的激励电压，重复上述各个的步骤。

3.2 实验结果

选取铝板上三条传感路径(7-16、6-12和2-11)的信号进行具体分析。钢块和螺栓均远离路径7-16，50 V与150 V电压激励作用时的Lamb波接收信号以及时间反转重构信号如图6所示。Lamb 波沿传感路径传播424 mm后被16号压电片接收，如图6(a), (b)。注意第一个波包是E/M耦合信号，时间反转处理时不做考虑。图6(c), (d)为归一化后的重构信号。对比重构信号的主波包和原始激励信号，如图7所示。由式(6)计算相关系数，低电压激励(50 V)、高电压激励(150 V)时的2个重构信号与原始激励信号间的相似度均达到98%。表明远离该路径的闭合型裂纹(螺栓)与线性散射体(钢块)均没有影响到Lamb波在该路径上的重构，路径7-16可以视为完整的主动传感路径。

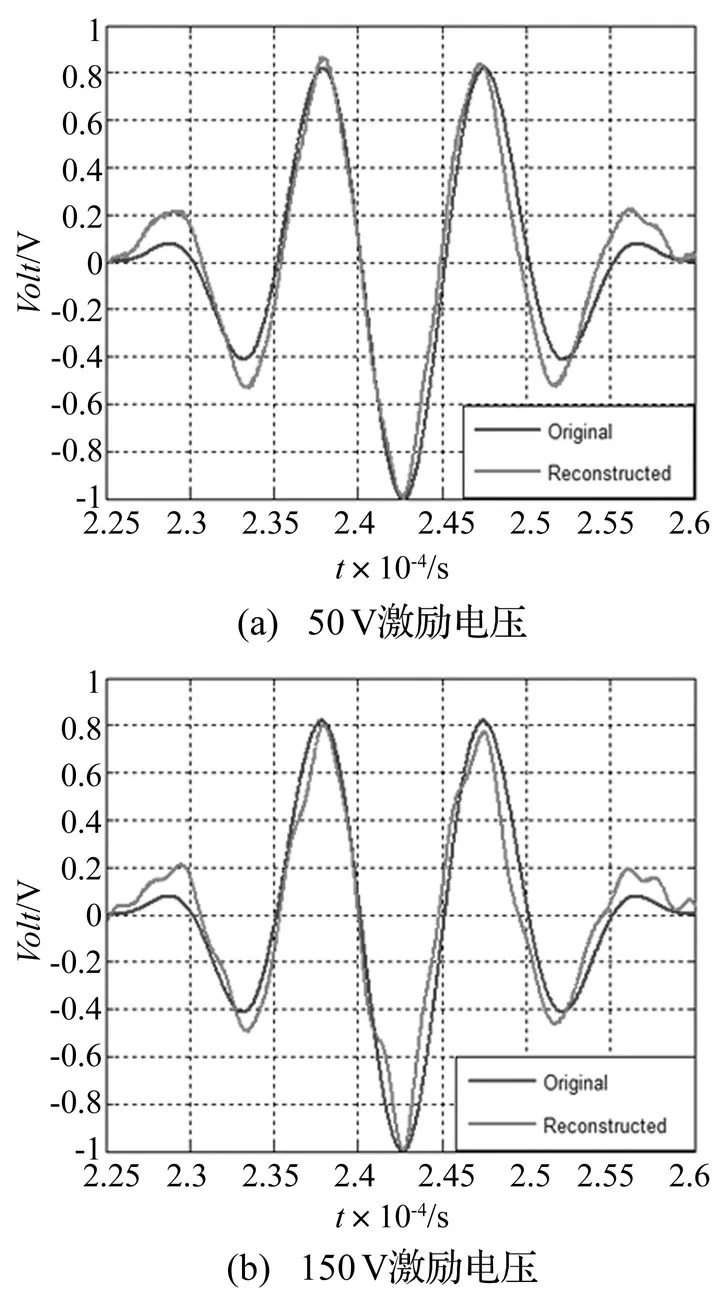
图7 路径7-16上原始激励信号与重构信号主波包比较 Fig.7 Original tone burst and reconstructed tone burst after time reversal procedure (Path7-16)

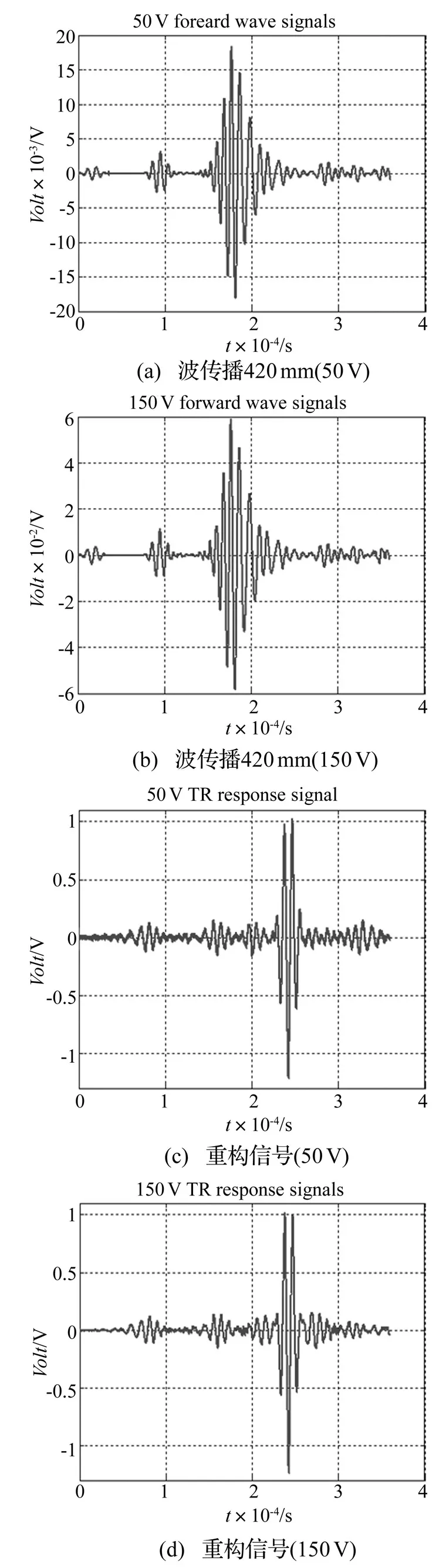
图8 路径6-12Lamb波时间反转过程Fig.8 The receive waves of Lamb wave time reversal procedure for the path P6-12

对于传感路径6-12，钢块在该路径上，而螺栓远离该路径。低电压与高电压分别激励时的Lamb波接收信号以及时间反转重构信号如图8所示。图8(a), (b)分别为低电压激励和高电压激励Lamb波沿传感路径传播420 mm后，12号压电片接收的响应信号。时间反转重构信号如图8(c), (d)所示。图9(a), (b)分别为2个重构信号的主波包与原始激励信号的对比。该传感路径上原始激励信号与2个重构信号的相似度与完整路径(7-16)时的相同，表明传感路径上存在线性散射体时(钢块)，尽管重构信号中的旁瓣信号波包有多个，但是波传播的线性互易性和时间可逆性依然成立，线性散射体的存在不会影响对非线性闭合型裂纹的检测。

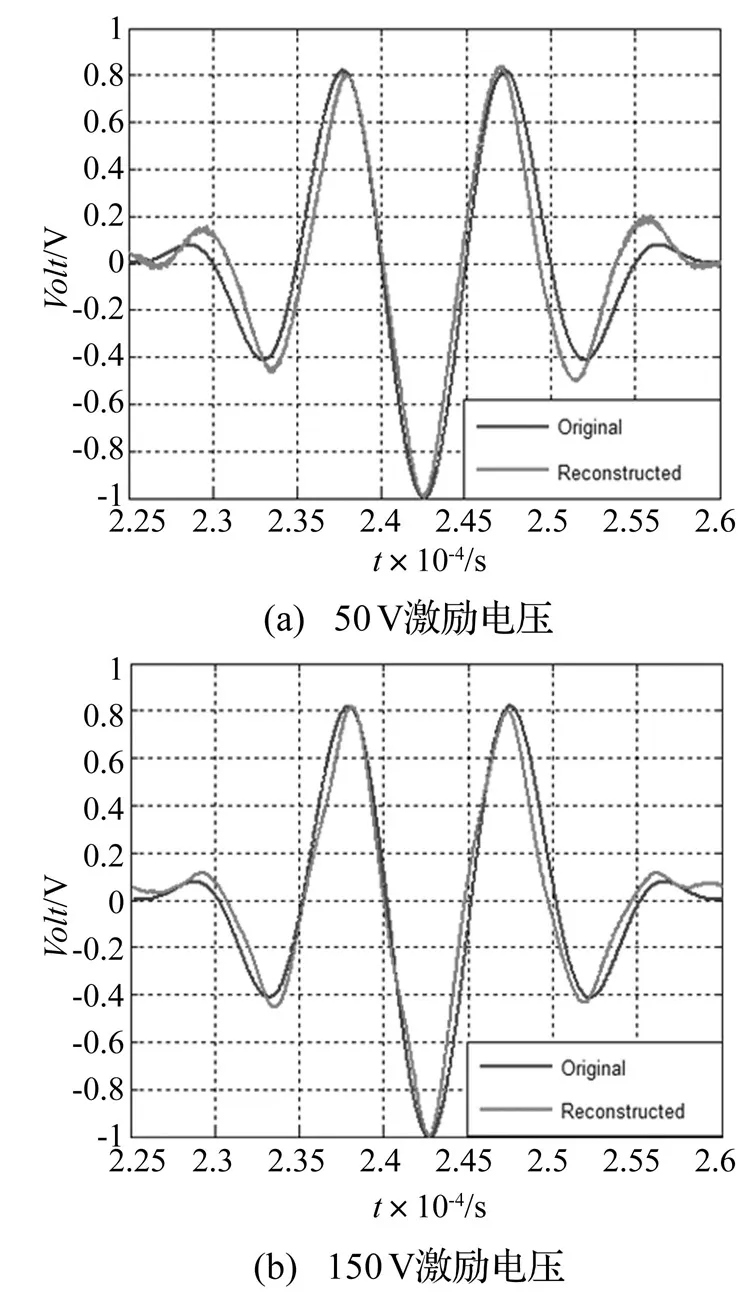
图9 路径6-12上原始激励信号与重构信号主波包比较Fig.9 Original tone burst and reconstructed tone burst after time reversal procedure for Path6-12

对于传感路径2-11，非线性的闭合型裂纹(螺栓)在该路径上。低激励电压(50 V)和高激励电压(150 V)激发的Lamb波时间反转的实验结果如图10所示。图10(a), (b)分别为2种电压激励下Lamb波传播424 mm后11号压电片接收到的波动信号，图10(c), (d)为2种情况下的时间反转重构信号。

图10 路径2-11Lamb波时间反转过程 Fig.10 Experimental response of Lamb wave time reversal procedure for path P2-11

闭合型裂纹在大幅值激励作用下裂纹界面开始部分张开与闭合，产生具有非线性特征的响应。提取150 V大激励电压作用下路径2-11上响应信号中的非线性成分，需要量化当前信号与线性参考信号间的差异。由于构件中疲劳裂纹程度不同，往往难以确定闭合型裂纹没有张开时线性参考信号的激励大小。本实验中用19 N·m扭矩固定螺栓在铝板上来模拟闭合型裂纹，50 V峰-峰值激励电压作用下，应力波幅值不足以张开该闭合型裂纹的两个界面, 响应是线性的，11号压电片接收到的波信号可以定义为瞬时基准信号VL。150 V峰-峰值的大电压激励作用下，应力波与闭合型裂纹的两个界面(螺栓和铝板间非良好的接触面)交互作用产生非线性响应，记录的波信号作为当前信号VH。路径2-11上的当前信号VH和基准信号VL如图11所示(VL乘以3)。为了消除板边界反射的影响，在选取时间窗口对记录信号进行时间反转时，反转信号中去除了图11所示的边界反射成分，50 V和150 V激励信号及其时间反转的重构信号分别如图12(a), (b)所示。由式(6)计算相关系数，低电压激励(50 V)、高电压激励(150 V)时的重构信号与原始激励信号间的相似度分别为98%和82%。图12表明，激励电压增大，闭合型裂纹被打开，重构信号与原始激励信号间的相似度显著降低，DI值增大；传感路径上存在非线性的闭合型裂纹时，波动的线性互易性不再成立，产生的非线性响应对Lamb波的重构有显著影响。

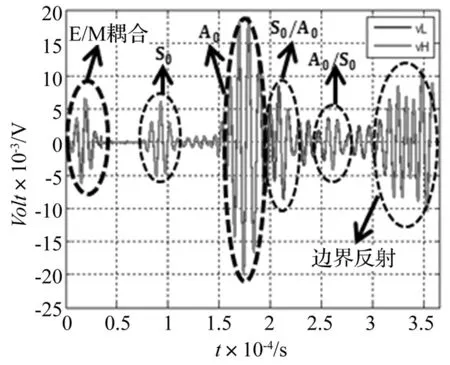
图11 50 V较小激励电压的基准信号vL与150 V较大激励电压的当前信号vHFig.11 Baseline signal vL(50 V excitation) and the current signal vH(150 V excitation)

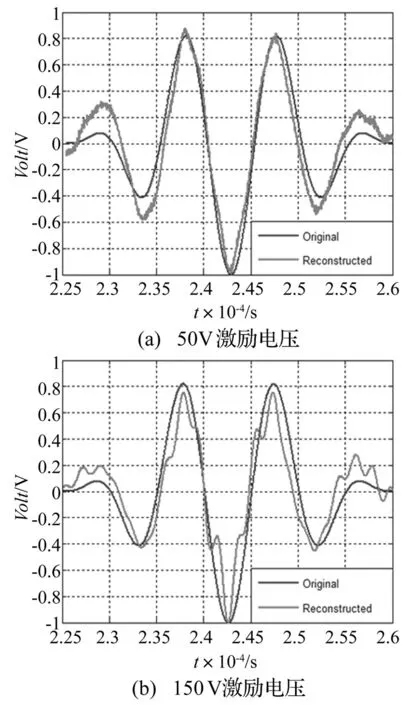
图12 路径2-11上原始激励信号与重构信号主波包比较Fig.12 Original tone burst and reconstructed tone burst of Path2-11 after time reversal procedure

上述非线性闭合型裂纹使得Lamb信号无法重构的结果可用来定位损伤位置。由2列16个压电传感器组成的主动传感网络中，理论上存在128条传感路径，根据波传播的互易性，实际上只有64条独立传感路径。随机选择16条路径，计算原始激励信号与重构信号间的相关系数，得到每条路径的损伤指数DI，如表1所示。将该板划分为1 000×1 000的像素点，利用式(10)计算每个像素点的值，形成如图13(a)所示的定位图(图中的像素值均进行了归一化处理)，像素值越大表示该点处存在损伤的可能性越大。图13(b)是利用全部64条传感路径得到的损伤定位图像，图中圆圈表示闭合型裂纹螺栓的实际位置，箭头表示估计的损伤位置。结果表明，本文所提出的非线性超声时间反转方法能准确识别并定位闭合型裂纹损伤。

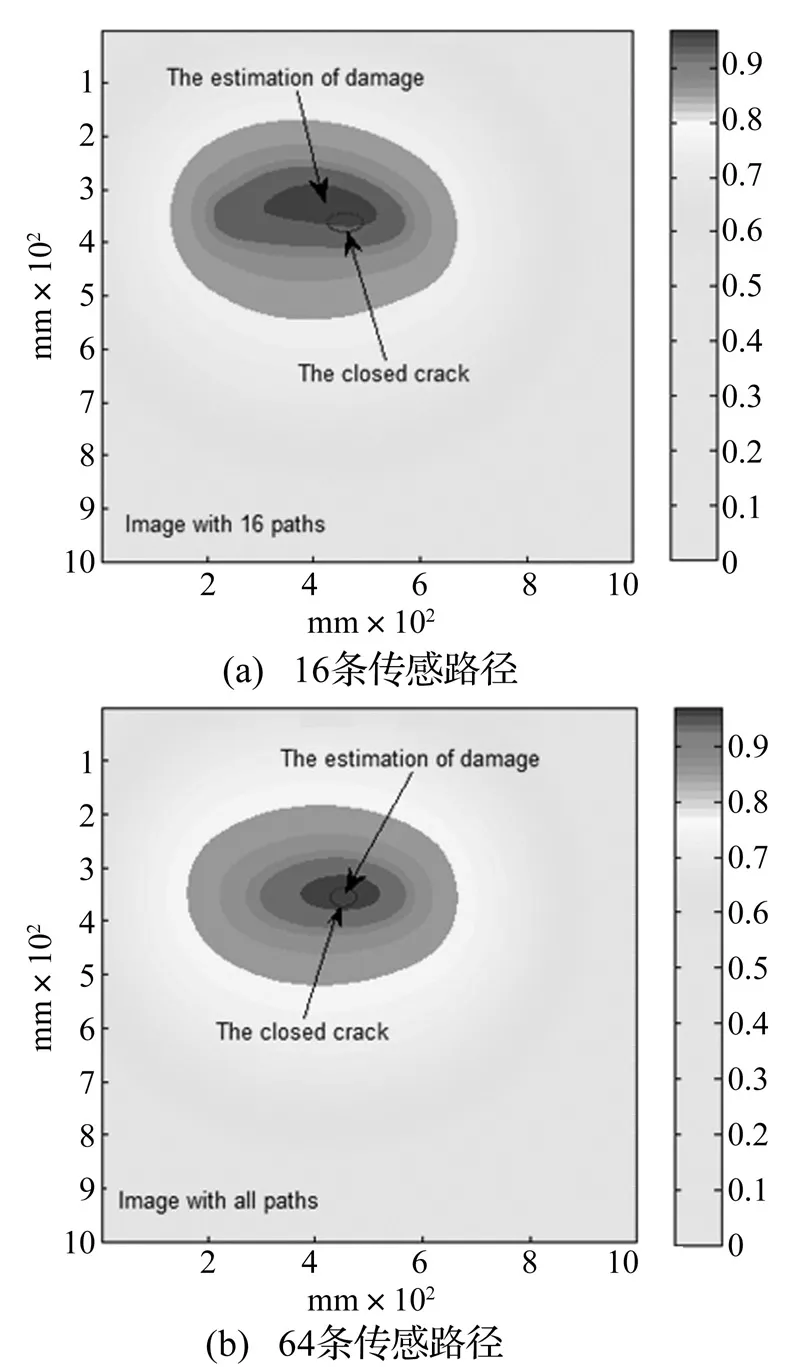
圆圈表示闭合型裂纹实际位置,箭头表示裂纹损伤的估计位置图13 闭合裂纹损伤定位图Fig.13 Image of damage constructed

4 结 论

本文提出了一种基于非线性超声时间反转理论识别和定位铝板结构中闭合型裂纹的方法， 进行相关实验验证了该方法。结果表明，在实际结构中使用简单的压电激励/传感阵列基于非线性超声时间反转理论的成像方法对非线性损伤定位和成像具有可行性，而且该方法利用比例相减原理不受波传播路径上线性散射体的影响。

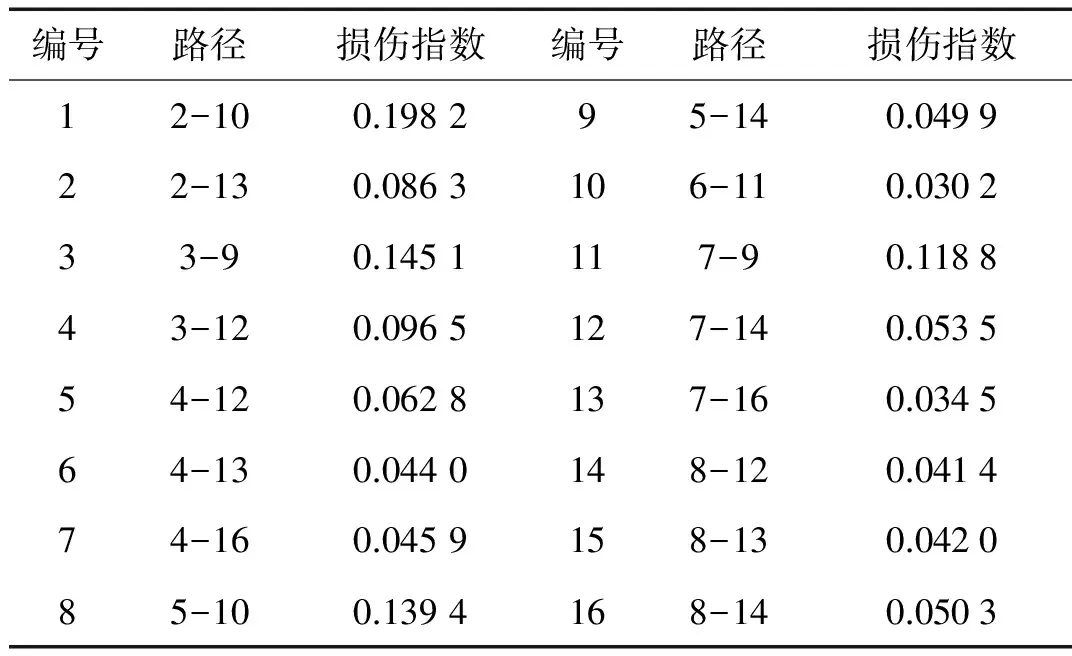
表1 不同传感路径上的损伤指数(DI)

[1] Ohara Y, Mihara T, Sasaki R, et al. Imaging of closed cracks using nonlinear response of elastic waves at subharmonic frequency [J]. Applied Physics Letters, 2007, 90(1): 011902-011902-3.

[2] Fink M. Time-reversed Lamb waves [J].Ultrasonics, Ferroelectrics and Frequency Control, IEEE Transactions on, 1998, 45(4): 1032-1043.

[3] Qiu L, Yuan S, Zhang X, et al. A time reversal focusing based impact imaging method and its evaluation on complex composite structures [J]. Smart Materials and Structures, 2011, 20(10): 105014.

[4] Cai J,Shi L,Yuan S,et al.High spatial resolution imaging for structural health monitoring based on virtual time reversal[J]. Smart Materials and Structures,2011,20(5): 055018.

[5] Fink M. Time recompression of dispersive Lamb waves using a time reversal mirror-application to flaw detection in thin plates[C]//Ultrasonics Symposium, 1996. Proceedings, 1996 IEEE. IEEE, 1996, 1: 659-663.

[6] Park H W, Kim S B,Sohn H. Understanding a time reversal process in Lamb wave propagation [J]. Wave Motion, 2009, 46(7): 451-467.

[7] Xu B,Giurgiutiu V. Single mode tuning effects on Lamb wave time reversal with piezoelectric wafer active sensors for structural health monitoring [J]. Journal of Nondestructive Evaluation, 2007, 26(2-4): 123-134.

[8] 王强, 袁慎芳, 邱雷. 基于时间反转理论的复合材料螺钉连接失效监测研究[J]. 宇航学报, 2007, 28(6): 1719-1723. WANG Qiang, YUAN Shen-fang, QIU Lei, et al. Study on bolt debonding monitoring of composite joint based on time-reversal method[J]. Journal of Astronautics, 2007, 28(6): 1719-1723.

[9] Ulrich T J, Johnson P A,Sutin A. Imaging nonlinear scatterers applying the time reversal mirror [J]. The Journal of the Acoustical Society of America, 2006, 119: 1514.

[10] Draeger C, Cassereau D, Fink M. Theory of the time-reversal process in solids [J]. The Journal of the Acoustical Society of America, 1997, 102: 1289.

[11] Fink M, Prada C. Acoustic time-reversal mirrors [J]. Inverse problems, 2001, 17(1): R1.

[12] Wang D, Ye L, Lu Y. A probabilistic diagnostic algorithm for identification of multiple notches using digital damage fingerprints (DDFs) [J]. Journal of Intelligent Material Systems and Structures, 2009, 20(12): 1439-1450.

[13] Mustapha S, Ye L, Wang D, et al. Debonding detection in composite sandwich structures based on guided waves [J]. AIAA Journal, 2012, 50(8): 1697-1706.

[14] Wang D, Ye L, Su Z, et al. Probabilistic damage identification based on correlation analysis using guided wave signals in aluminum plates [J]. Structural Health Monitoring, 2010, 9(2): 133-144.

Time reversal based damage detection for closed crack

ZHANG Wang, WU Wei-liang, XIAO Li, QU Wen-zhong

(Department of Engineering Mechanics, Wuhan University, Wuhan 430072, China)

Initial cracks in metallic structures incline to be closed at rest. Such incipient damage generally fails to be detected and located with traditional linear ultrasonic techniques because ultrasonic waves can penetrate the contact interface of closed cracks. An imaging algorithm based on nonlinear ultrasonic time reversal method was proposed to detect closed cracks in aluminum plates. Two surface-bonded piezoelectric transducer (PZT) arrays were used to generate, receive and re-emitted ultrasonic wave signals. The closed crack was simulated by tightening a bolt on the aluminum plate. By applying large amplitude excitation voltage on the PZT transducers, the closed crack could be opened and closed. The signals of transmitted waves recorded by PZT array, containing nonlinear components, were time reversed, emitted back, and the tone burst reconstructions were achieved. The correlation coefficient between the original excitation signal and the reconstructed signal was calculated to define the damage index for individual sensing path, and was further used to develop an imaging algorithm to locate the closed crack on the plate. The experimental results demonstrate that incident wave signals and their reconstructed signals can be used to accurately detect and locate closed cracks.

closed crack; structural health monitoring; damage detection; nonlinear time reversal; PZT array

国家自然科学基金资助(51078293,51378402)

2013-11-29 修改稿收到日期：2014-05-20

张望 男，硕士生，1991年3月生

屈文忠 男，教授，博士生导师，1968年生

TH212；TH213.3

A

10.13465/j.cnki.jvs.2015.09.017