建筑物内爆泄压口冲击波参数工程算法研究

汪 维, 刘瑞朝, 吴 飚, 周朝阳

(总参工程兵科研三所，河南 洛阳 471023)

建筑物内爆泄压口冲击波参数工程算法研究

汪 维, 刘瑞朝, 吴 飚, 周朝阳

(总参工程兵科研三所，河南 洛阳 471023)

建筑物内部爆炸泄压口冲击波参数的确定对于建筑物结构毁伤评估具有重要的作用，一旦泄压口冲击波参数确定以后，即可利用相应毁伤判据快速评估泄压口附近结构和设备的毁伤程度。由于内部爆炸波是初始爆炸波经过建筑物内壁面多次反射叠加作用的结果，在泄压口会形成不同于自由场的冲击波，目前还未有泄压口冲击波参数成熟的快速工程算法。为了分析泄压口冲击波参数、总结相应快速经验工程算法，在量纲分析的基础上，提出影响泄压口冲击波峰值压力和冲量相关的无量纲参数。然后利用首先利用AUTODYN软件数值仿真研究了特定当量内爆炸作用下冲击波形成的过程，分析了泄压口部冲击波压力波形，并研究了泄压口的冲击波峰参数与不同结构参数之间的关系，最后在大量数值计算的基础上总结了泄压口的冲击波参数的经验公式，为建筑物内爆毁伤评估奠定基础。

建筑物内爆;量纲分析;工程算法;数值模拟;AUTODYN

随着制导武器种类迅速增加，命中精度大幅提高，作战效能有力提升，如何科学准确预测弹药建筑物内部爆炸泄压口冲击波参数，直接影响到建筑物内部爆炸毁伤效果的预测与评估。而在内部爆炸环境下，作用于建筑结构上泄压口的爆炸载荷受建筑物的复杂结构分布，如不同的房间结构、房间开口大小及分布等以及冲击波与建筑结构相互作用等众多因素的影响，因此爆炸内爆载荷的泄压口冲击波参数研究是一个技术难点[1]。

建筑物遭受爆炸作用的毁伤分析中，关键因素之一就是如何确定爆炸载荷作用的方式和大小。由于内部爆炸波是初始爆炸波经过建筑物内壁面多次反射叠加作用的结果，在泄压口会形成不同于自由场的冲击波，目前还未有泄压口冲击波参数成熟的快速工程算法。Beshara[2-3]对结构内爆炸做了较全面的回顾，可以看出内爆的研究成果主要集中在上世纪70、80年代。近期的研究则主要是基于数值模拟方法[4-5]，针对特定问题进行研究，但对于内爆泄压口载荷模型的研究很少。

本文研究目的是通过对爆炸冲击波与建筑物房间相互作用的研究，建立在封闭房间内部爆炸环境下作用于泄压口部的爆炸载荷工程算法。首先，在量纲分析的基础上，提出影响泄压口冲击波峰值压力和冲量相关的无量纲参数。然后运用AUTODYN有限元显式动力分析软件[6]建立包括TNT炸药，空气和房间结构在内的三维有限元模型，并对TNT炸药的爆轰，在空气中的传播以及与房间结构的相互作用进行模拟，并对参数分析研究爆炸波和房间结构尺寸的相关参数对爆炸波与柱相互作用的影响。最后，在有限元模拟数据的基础上，采用曲线拟合方法，建立预测房间结构内爆泄压口部爆炸载荷参数的公式。

1 量纲分析

内爆泄压冲击波压力问题可以写成如下函数形式描述：

Pm=f(S,V,ω,R,ρ0,ρe,Ee,P0)

(1)

其中:Pm为泄出峰值压力；S为结构开口总面积；V为结构总的容积；ω为装药TNT当量；R为爆距；ρ0为空气密度；ρe为TNT装药密度；Ee为单位质量装药所释放的化学能；P0为初始大气压力，图1给出了开口的约束空间内爆炸示意图。

使用π定律，并选择合适的主变量，采用L-M-T度量单位系统作为基本量纲，则：

[Pm]=L-1MT-2[S]=L2
[V]=L3[ω]=M
[R]=L[ρ0]=L-3M
[ρe]=L-3M[Ee]=L2T-2
[P0]=L-1MT-2

(2)

Π=F(Π1,Π2,Π3,Π4,Π5)

(3)

其中:

(4)

把式(4)代入(3)中得：

(5)

图1 建筑物内爆结构示意图Fig.1 Schematic diagram of internal building blast

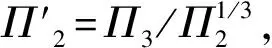
(6)

内爆泄压口冲击波正压冲量问题可以写成如下函数形式描述：

Im=f1(S,V,ω,R,ρ0,ρe,Ee,P0)

(7)

其中:Im为泄出正压冲量；S为结构开口总面积；V为结构总的容积；ω为装药TNT当量；R为爆距；ρ0为空气密度；ρe为TNT装药密度；Ee为单位质量装药所释放的化学能；P0为初始大气压力。

采用上述相同的分析方法，内爆泄压口冲击波正压冲量工程化近似为：

(8)

目前，试验中泄压口部的压力测量数据很少，很难进行经验公式的拟合，而美军TM5-1300手册[7-8]中的部分图表数据虽然给出了不同结构尺寸外部冲击波参数的经验图，但往往是泄压口外部距泄压口一定距离的冲击波参数，直接用于泄压口冲击波参数的经验图表比较少，因而采用在数值模拟方法试验验证的基础上，补充数值模拟计算可以解决拟合经验公式数据源不足的问题。

2 有限元数值模拟计算

目前，爆炸问题的计算通常采用拉格朗日法或欧拉法。拉格朗日法中的运动方程形式比较简单，容易建立精度较高而又稳定的格式。而且，拉格朗日法跟踪固定的介质，可以用来计算包含多种物质的系统，不同物质间的界面能清晰地表示出来，自由面的处理也很方便。因此本文采用拉格朗日网格模拟结构构件。欧拉方法采用固定的网格，物质在网格中流动，更适用于计算流体以及严重扭曲的问题。本文采用欧拉网格模拟炸药及空气。

在本文中，运用AUTODYN软件模拟爆炸波传播及其与房间结构的相互作用。由于爆炸冲击波与房间结构的相互作用很复杂，为了简化分析问题，在研究之前，提出以下假设：

(1) 仅考虑房间内爆炸。即炸药假定为球形装药，放置在房间内距各房间内壁一定距离处，爆炸产生的冲击波直接与结构产生相互作用；

(2) 房间结构为方形房间单开口结构，且在爆炸荷载作用下房间结构不发生破坏，保证爆炸冲击波传播到泄压口时，泄压面积不发生改变。

2.1 有限元模型

数值模拟从炸药的爆轰以及爆炸冲击波在空气中的传播开始，直至爆炸冲击波传播到结构构件所在位置并与之发生相互作用，继而向更远处传播为止。为了节省轴对称过程数值模拟的计算量，采用了两步模拟方法。① 利用一维模型模拟对球面爆炸波到达目标壁面之前进行数值模拟，直至传播到结构构件前但尚未和结构构件发生相互作用。② 利用AUTODYN[6]特有的映射功能，将先前一维模拟的结果映射并重现到三维模型中，形成三维的爆炸冲击波。随后，在三维模型中，模拟爆炸冲击波与结构构件的相互作用。这种两步模拟法较之完全的三维模拟，可以采用较少数量的网格、较小的网格尺寸，但同样获得准确的模拟结果，因此，对于整个模拟过程而言不仅能够有效提高计算效率，而且能够提高计算结果的精度。本文以柱为例进行计算，其它构件(板、梁、墙等)可以参考柱的计算结果。

图2 一维有限元模型及其结果向三维有限元模型的映射Fig.2 One-dimensional finite element model and the remap of one one-dimensional results to three-dimensional model

图2分别给出了模拟炸药爆轰以及爆炸冲击波传播的一维有限元模型以及将一维模型计算结果映射到三维模型中后的爆炸冲击波示意图。从图1中可以清楚地看出在爆炸冲击波与柱发生相互作用前，一维有限元模拟的结果映射到三维有限元模型中的情形，形成的三维爆炸冲击波可以用于爆炸冲击波与结构构件相互作用的模拟和计算。

在数值模拟中，由于结构的对称性，三维结构采用1/4计算模型进行计算，炸药和空气采用欧拉网格模拟，边界采用物质流出边界条件。柱采用拉格朗日网格模拟。利用AUTODYN提供的欧拉/拉格朗日全接触算法模拟爆炸波与柱的相互作用。

2.2 材料模型及参数

数值模拟中，TNT炸药的材料模型用JWL状态方程来描述，其方程如下：

(9)

式中：P为爆轰产物压力，V是相对体积，E是单位质量的内能，A，B，R1，R2和ω是材料常数。TNT炸药JWL状态方程参数[6]见表1所示。

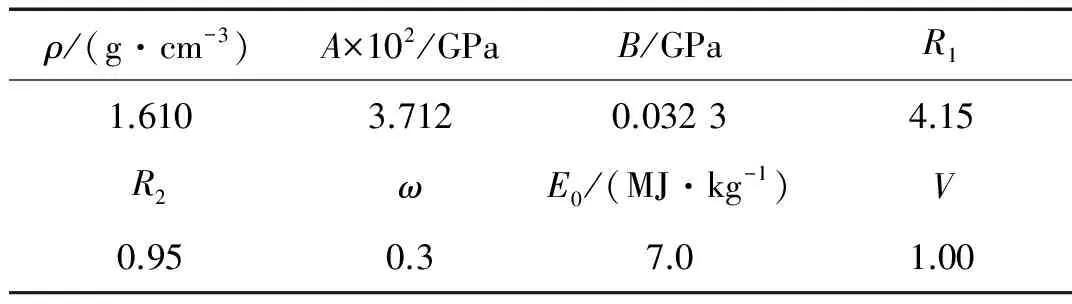
表1 TNT炸药模型材料的参数

空气采用理想气体状态方程描述。其压力P和能量e的关系可由下式确定：

P=(γ-1)ρe

(10)

式中：ρ为空气的密度，e为气体单位质量的内能，γ为材料常数。表2给出了具体材料参数。

表2 空气材料参数

国内其他学者的研究表明结构构件的刚度和变形并不能显著影响作用于构件上的爆炸载荷[9]。因此，当采用有限元模拟方法模拟爆炸波与结构的相互作用时，可以假定结构为刚体，约束构件所有自由度，从而提高计算效率。

2.3 数值模拟方法验证

对爆炸波的传播过程以及其与结构的相互作用进行数值模拟时，模拟结果的准确度在很大程度上取决于采用的网格尺寸和算法。因此，在大多数情况下，在数值模拟之前，都应该进行数值试验验证，从而找到可以接受的网格尺寸和算法。

为了验证爆炸冲击波传播及其与结构柱相互作用的数值模拟方法，利用该方法对Chapman等[10]做的爆炸试验进行数值模拟。图3给出了爆炸试验的布置图及有限元计算模型，试验中使用压力传感器测试一定TNT装药量在某一爆高空中爆炸抗爆墙后目标表面上目标点的反射压力参数。其中Ht为30 cm，抗爆墙高度Hl为30 cm，de和dw分别为60 cm，爆高为15 cm，装药量为60 g。数值模拟中网格大小取1 cm，并将数值模拟结果与试验结果进行对比分析。

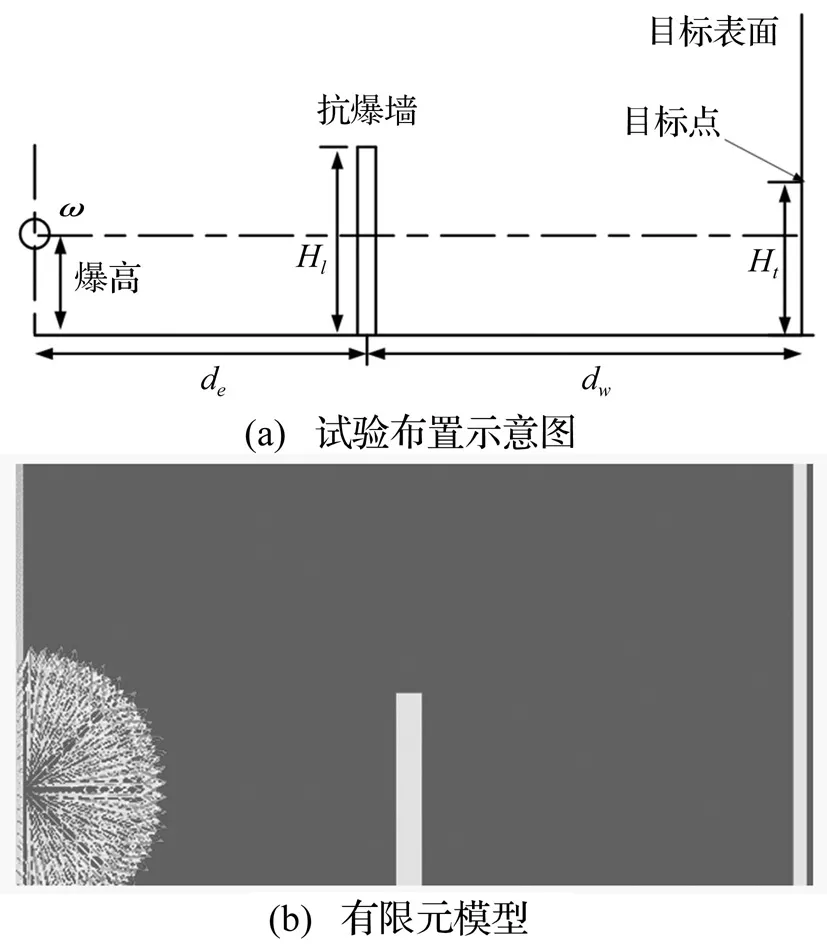
图3 爆炸试验布置图及有限元模型Fig.3 The set-up of blast experiment and finite element model

图4比较了数值模拟和试验得到的目标点反射超压的时程曲线，从图中可以看出，数值模拟得到的反射超压时程曲线和试验结果吻合较好，两次反射超压峰值大小以及到达的时间与试验结果吻合较为一致。与试验结果相比，数值模拟得到的反射超压由0上升到最大值的时间略长，正峰值超压的数值略小。这是由于本试验的炸药起爆位置和目标点的实际距离很小，尽管如此，数值模拟的结果仍与试验结果比较吻合，这进一步说明本文提出的数值模拟方法以及网格大小的适用性，可以用于爆炸冲击波传播及与结构相互作用的数值模拟计算。

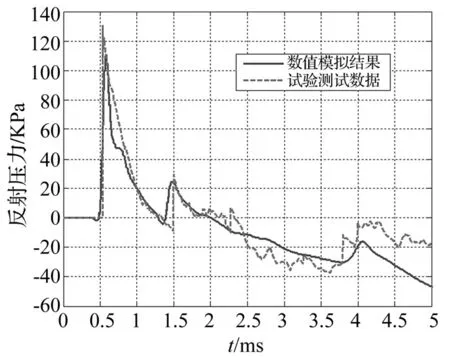
图4 目标测试点反射压力时程曲线试验和数值模拟结果对比Fig.4 Compare of reflect pressure of gauge point of numerical result with experiment result

图5 爆炸波传播与结构壁面相互作用过程Fig.5 The process of blast wave spread and interaction with structure faces

2.4 典型数值模拟结果

通过数值模拟，得到了大量的关于爆炸冲击波传播以及爆炸冲击波与房间结构相互作用的数据，这里仅给出一些典型的数值模拟结果。计算模型选取典型建筑物房间结构，房间大小为3.5×3.5×3.5 m3，开口大小为1.5×1.5 m2，TNT装药量为15 kg，球形装药房间中心爆炸。

图5出了爆炸波的传播及其与房间结构的相互作用过程，从中可以清楚看到爆炸波传播以及与房间结构相互作用的全过程。在t=600 μs，爆炸冲击波仍沿半球状向外传播；在t=900 μs，爆炸冲击波传播至房间墙前表面，在墙前表面形成反射波，冲击波压力急剧增强，在泄压口冲击波则继续向外传播；在t=1 300 μs，爆炸冲击波传播至房间四角，四角压力急剧增加；在t=2 100 μs，爆炸冲击波在房间四角反射后继续反向传播；在t=2 400 μs，在四面墙表面反射的冲击波汇聚形成中心高压区域；在t=2 900 μs，冲击波再次沿泄压口向外传播，泄压口迎来第二次反射的冲击波，此后冲击波压力随着在房间内来回反射逐渐降低至大气压。

图6 泄压口冲击波压力历史Fig.6 Shock wave pressure history of venting area

泄压口冲击波压力历史如图6所示，可以发现随着冲击波在房间内来回反射传播，泄压口的冲击波压力出现抖动而逐渐降低，主要原因是冲击波在房间内壁来回反射，造成了泄压口冲击波压力出现了多次峰值压力且峰值压力逐渐降低。在时间t=50 ms时刻降低至200 kPa，最终泄压口冲击波压力降低至大气压力。在泄压口中心(图6(a)所示)和边缘(图6(b)所示)冲击波压力波形接近一致，峰值压力误差不超过15%，因而可以近似泄压口冲击波压力和冲量与泄压口测点位置无关。

3 泄压口部冲击波参数计算结果

为了补充拟合经验公式所需的冲击波参数数据，对不同装药量、不同房间开口面积情况下房间结构内爆进行了数值模拟计算，典型工况如图2所示，计算过程中记录泄压口部冲击波压力历史曲线。

研究结果表明，随着比例泄压面积的减小，泄压口峰值压力和冲量均呈现增加的趋势；随着单位体积装药比减小，泄压口峰值压力和冲量均呈现减小的趋势；而泄压口距爆心比例距离的增加，泄压口峰值压力和冲量均呈现减小的趋势，计算结果如表3所示。

用最小二乘法进行拟合得到的冲击波峰值压力的计算公式为：

(11)

本文的拟合公式在置信度99%水平下，相关系数为0.972，F检验为1 020.7，F0.01为6.63，F≫F0.01，相对误差值大小与数值模拟结果对比如图7所示，其中n为数据源数目，这说明拟合式(11)和数据源吻合得较好。

图7 内爆泄压峰值压力拟合相对误差示意图Fig.7 The relative error of peak pressure in venting area of internal blast

用最小二乘法进行拟合得到的冲击波正向冲量的计算公式为：

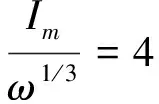
(12)

本文的拟合公式在置信度99%水平下，相关系数为0.981，F检验为1 528.1，F0.01为6.63，F≫F0.01，相对误差值大小与数值模拟结果对比如图8所示，这说明拟合式(12)和数据源吻合得较好。

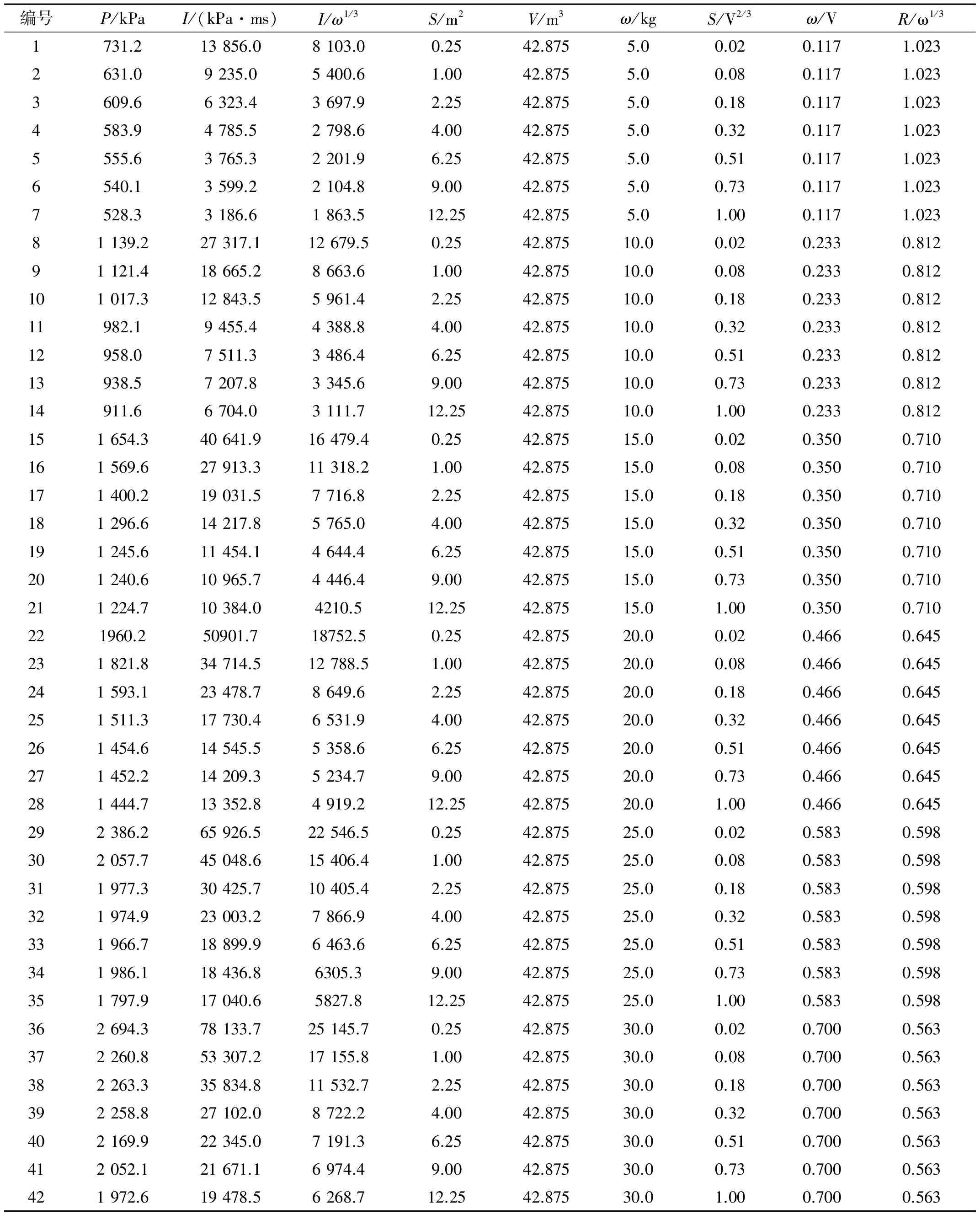
表3 内爆泄压数值模拟结果

图8 内爆泄压冲量拟合相对误差示意图Fig.8 The relative error of impulse in venting area of internal blast

应当注意的是，上述拟合的经验公式仅仅适用于常规间室结构(2 m≤L≤9 m)，并且比例泄压面积0.02≤S/V2/3≤1的情况。对于无限开口的情况则采用自由场冲击波参数经验公式进行计算，对于完全封闭的情况则采用封闭内爆经验公式进行计算，对于狭长坑道形式则采用坑道内爆冲击波参数经验公式进行计算。

4 结 论

本文通过数值模拟，主要研究了在建筑物房间内部爆炸环境下，爆炸波的传播以及爆炸波在传播过程中与房间结构相互作用的过程，并在量纲分析的基础上，提出了预测房间泄压口上爆炸载荷各参数的公式。主要结论如下：

(1) 通过量纲分析，总结提出了影响建筑物内爆泄压口冲击波参数的无量纲参数，为后续总结冲击波参数工程算法提供基础。

(2) 通过显式有限元动力分析软件AUTODYN数值模拟了爆炸波传播及其与房间结构的相互作用过程。研究结果表明，随着冲击波在房间内来回反射传播，泄压口的冲击波压力出现抖动而逐渐降低，爆炸压力作用时间较自由场有较大增加。

(3) 随着比例泄压面积的减小，泄压口峰值压力和冲量逐渐增加；随着单位体积装药比减小，泄压口峰值压力和冲量逐渐减小；而泄压口距爆心比利距离的增加，泄压口峰值压力和冲量逐渐减小。

(4) 在有限元模拟数据和量纲分析的基础上，提出了预测结构表面特征处爆炸载荷各参数(正反射峰值压力和冲量)的公式，为建筑物内爆毁伤评估奠定基础。

[1] SMITH P D, ROSE T A. Blast wave propagation in city streets-an overview[J]. Progress in Structural Engineering and Materials, 2006, 8(1): 16-28.

[2] BESHARA F B A. Modeling of blast loading on aboveground structures-Ⅰ.General phenomenology and external blast[J]. Computers and Structures, 1994, 51(5): 585-596.

[3] BESHARA F B A. Modeling of blast loading on aboveground structures-Ⅱ. Internal blast and ground shock[J]. Computers and Structures, 1994, 51(5): 597-606.

[4] Zhao C F, Chen J Y, Wang Y, et al. Damage mechanism and response of reinforced concrete containment structure under internal blast loading[J]. Theoretical and Applied Fracture Mechanics, 2012, 61: 12-20.

[5] FELDGUN V, KARINSKI Y, EDRI I, et al. On blast pressure analysis due to a partially confined explosion: Ⅱ. numerical studies[J]. International Journal of Protective Structures, 2012, 3(1): 61-80.

[6] AUTODYN. Theory manual[M]. Century Dynamics, 2006.

[7] TM5-1300. Structures to resist the effects of accidental explosions[R]. US Department of the Army 1990.

[8] UFC-3-340-02. Structures to resist the effects of accidental explosions[R]. US Department of Defense 2008.

[9] SHI Y C, HAO H, LI Z X. Numerical simulation of blast wave interactionwith structure columns[J]. Shock Waves, 2007, 17: 113-133.

[10] CHAPMAN T C, ROSE T A, SIMTH P D. Refleced blast wave resultants behind cantilever walls: a new prediction technique[J]. International Journal of Impact Engineering, 1998, 16(3): 397-403.

Engineering arithmetic for internal blast waves parameters in venting area of building structures

WANG Wei, LIU Rui-chao, WU Biao, Zhou Chao-yang

(The Third Engineering Scientific Research Institute of the Headquarters of the General Staff, Luoyang 471023, China)

The blast waves parameters in venting area are important in damage assessment of building structures under internal blast. Once the blast waves parameters are certain, the damage level of structures and equipments near the venting area can be assessed. As internal blast wave is the superposition of multi-reflectied waves of initial blast by the inner surfaces of building structure, and the blast waves in venting area is not of the same character as free air blast waves, the traditional engineering arithmetic for blast waves parameters in venting area is not yet applicable. In the paper, based on dimensional analysis, the relationship between venting area blast wave parameters and different structure parameters was analyzed. Then the internal blast shock wave of building structure was simulated by using AUTODYN software. The evolutionary process of internal blast wave was investigated and the blast pressure wave profile in venting area was analyzed. Based on a large number of numerical simulations, the empirical equations for venting area shock waves parameters were summarized, and they can be used as the base of damage assessment of internal building blast.

building internal blast; dimensional analysis; engineering arithmetic; numerical simulation; AUTODYN

国家自然科学基金资助项目(11302261)

2013-12-19 修改稿收到日期：2014-04-30

汪维 男，博士，助理研究员，1983年生

刘瑞朝 男，博士，研究员，1965年生

O383

A

10.13465/j.cnki.jvs.2015.09.009