基于混沌振荡粒子群优化的FCM文本聚类方法

符保龙

(柳州职业技术学院 电子信息工程系，广西 柳州 545006)

0 引言

Internet包含了大量的数据，如何快速的寻找到用户关心的信息是当前数据挖掘研究的一个重要问题。模糊聚类分析是一种无监督的方法，它根据一定的规则自动对数据进行分类。特别是模糊C均值聚类(Fuzzy C－Mean，简称FCM)算法，它具有模糊处理能力，算法简单、运算速度快，在很多领域得到了大量应用。FCM算法聚类效果受初始值影响较大，且算法采用梯度下降对目标函数进行优化，而目标函数具有多峰值，使得算法易于陷入局部极值。很多专家学者对FCM算法进行了改进，文献［1］提出了一种NSFCM算法，该方法通过计算样本的平均信息熵确定最终的聚类数，使用密度函数设定FCM算法的初始聚类中心，具有较高的聚类精度和执行效率;文献［2］提出了一种基于粒子群算法的模糊均值聚类方法，该方法利用粒子群优化算法(Particle Swarm Optimization，简称PSO)优化模糊均值聚类算法，获得了较好的文本聚类效果，但PSO算法自身的缺点也影响了FCM算法的聚类效果;文献［3］提出了一种基于多样性策略的粒子群算法，该算法设计了一种吸引和排斥机制对粒子的速度进行更新，同时引入物理学中的反弹理论设计了一种反弹机制，该机制能将解空间外的粒子反弹回解空间内，充实了群体粒子的多样性，有利于算法搜索到全局最优解。

在文献［1－3］的启发下，为了解决FCM算法受聚类中心初始值影响大的问题，同时也为了避免标准PSO算法易于陷入早熟的缺点，本文引入混沌思想对PSO算法进行优化，在寻优的过程中利用一个振荡环节来提升PSO算法的全局收敛性。把改进的PSO算法和FCM算法相结合，提出一种基于混沌振荡粒子群优化的模糊C均值聚类算法(Chaos Concussion Particle Swarm Optimization Fuzzy C－Mean Algorithm，简称CCPSO－FCM)。实验结果表明，CCPSO－FCM算法运行速度更快，对大样本的数据具有更好的聚类效果。

1 FCM算法的基本原理

FCM算法是在经典C均值聚类算法的基础上发展而来的，与C均值聚类算法不同在于FCM引入隶属度的概念，样本中的数据点通过隶属度来进行归类。设有样本集X={x1，x2，…，xn}，根据要求把样本集X划分m类，m是常数且m＞1。如果第i个样本点属于第i类的隶属度用uij表示，且0≤uij≤1，此时X就可以用模糊矩阵U来表示，即:U=(uij)。当满足条件0＜uij＜n，此时FCM的目标函数就可以定义为:

其中Aj(j=1，2，…，m)表示样本的聚类中心，b(b＞1)是模糊指数。

公式(1)的约束条件为:

在公式(2)的约束下，通过引入拉格朗日乘子求解公式(1)可得:

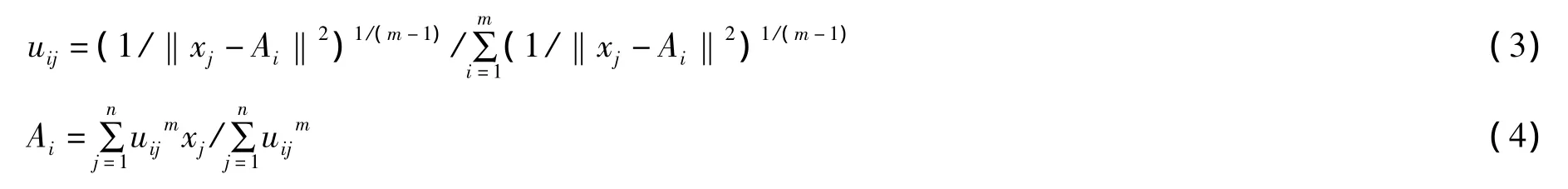
在公式(3)、(4)中，i=1，2，…，m，j=1，2，…，n。

FCM算法的思想就是通过迭代公式(3)和公式(4)，使得目标函数j(u，A)最小。FCM每一次迭代都使得目标函数j(u，A)减小，这种梯度下降的方式使算法易于陷入局部极小值，特别是样本数量较大的时候，陷入局部极值的问题更加明显。而且这种算法的目标函数j(u，A)可能有多个极值，聚类初始值的选取对最终聚类的结果会产生很大影响。

2 混沌因子和振荡因子优化的PSO算法基本原理

PSO算法源于对鸟群寻找食物行为的观察研究，它是一种全局寻优方法，具有结构简单、速度快且具备并行搜索能力，对问题的求解精度高。但PSO算法也存在学习因子不稳定的问题，该原因将导致群体内的个体在某个局部过多的徘徊，此时群体内的其它个体将会向同一位置聚集，从而使算法陷入早熟。针对PSO算法存在的问题，我们引入一个振荡环节来提升PSO算法的全局搜索性能［4－5］，利用混沌理论来优化PSO算法的局部搜索能力。

标准PSO算法更新粒子速度和位置的方程如下:

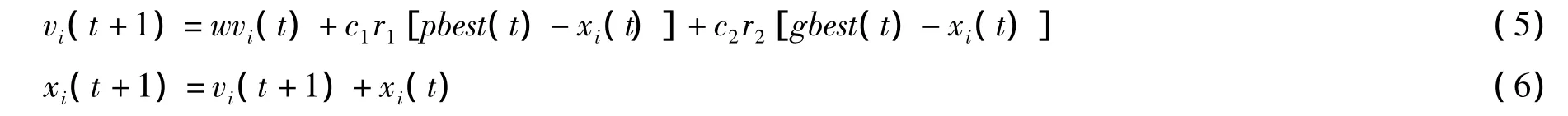
其中，w称为惯性权重，一般其值都是从0.9线性变化到0.4;c1=c2=2，它们称为加速常数;r1和r2是两个随机数，且r1∈［0，1］、r2∈［0，1］;pbest(t)和gbest(t)分别表示t时刻粒子群中个体的最优值和全局最优值。

为了解决标准PSO算法易于陷入早熟的问题，引入一个振荡环节，此时公式(1)可转变为:

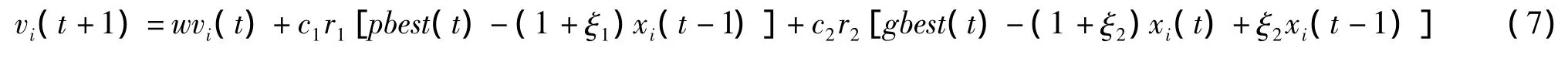
在公式(7)中，ξ1和ξ2称为振荡系数，它们的值随着进化代数的不同取不同的值，以此来保证PSO算法能保持种群的收敛性和多样性，从而保证算法全局搜索和局部搜索的性能。为了能更好的描述问题，我们假定g表示当前进化代数，Gmax表示算法设定的最大进化代数，ξ1和ξ2的取值分两种情况:

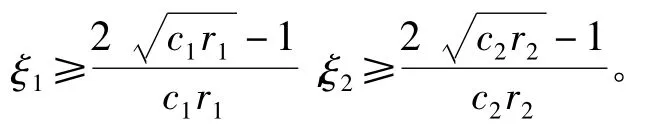
为了能进一步保证PSO算法的多样性，我们还引入了混沌理论对粒子的pbest和gbest进行优化，具体优化步骤如下:

Step 1:令k=0，将待优化的粒子xkj通过公式(8)转换到区间［0，1］内;

其中i=1，2，…，n，j=1，2，…，m，第j维粒子搜索所能达到的上、下界分别用xmin，j和xmax，j表示;

Step 2:把Step1得到的数据用Logistic函数映射成为混沌系列:

Step 3:利用公式(10)对混沌变量sk+1j进行映射，经过转换后xk+1j称为决策变量:

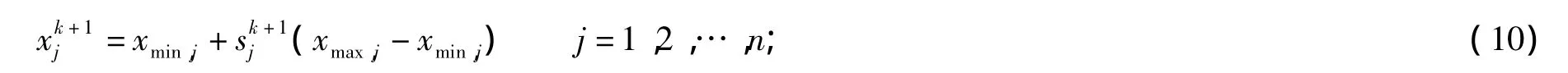
Step 4:对Step3中得到的序列进行评估，选取适应度最高的粒子和当前的粒子进行比较，如果优于当前解则进行替换，否则保留当前粒子并令k=k+1，然后跳转到Step2。

根据以上的讨论，引入振荡环节和混沌理论的PSO算法的步骤如下:

Step1:随机初始化种群中粒子的位置，利用公式(7)计算粒子的速度;

Step2:计算种群内所有粒子的适应度，并保存各自的位置和速度，把适应度值最高的粒子的位置和适应值保存在gbest中;

Step3:更新所有粒子的速度和位置;

Step4:再次计算所有粒子的适应度并降序排序，保留前面20%的粒子;

Step5:按本文所讨论的混沌步骤更新粒子的pbest和gbest;

Step6:如果满足设定的阈值或达到最大进化代数，则输出计算结果，算法结束，否则，跳转到Step2。

3 基于混沌振荡粒子群优化的FCM算法

3.1 粒子编码

CCPSO－FCM算法的目标是确定最优的聚类中心，因此算法中的粒子采用实数编码，每一个粒子分别表示每一个待确定的聚类中心Aj(j=1，2，…，m)，对于一个样本集X={x1，x2，…，xn}来说，如果用aij来表示第i个粒子的第j个聚类中心，则样本集X的聚类中心可以形成一个集合Zi=(ai1，ai2，…，aim)。

3.2 适应度函数

为了简化问题，我们使用如下的函数作为CCPSO－FCM算法的适应度函数。即:

公式(11)表明，如果J(u，A)的值越小，则粒子群中个体适应度值越大，即CCPSO－FCM算法的聚类效果越好。

3.3 CCPSO－FCM算法的具体实现步骤

CCPSO－FCM算法的具体执行步骤如下:

Step1:初始化算法的各种参数，如:聚类中心类别m、模糊加权指数b、粒子群规模N等;

Step2:随机生成粒子的初始位置Zi并初始化它们的速度vi;

Step3:根据公式(3)、(4)计算各样本的隶属度;

Step4:利用公式(11)计算所有粒子的适应度;

Step5:执行本文设计的混沌振荡环节来更新粒子的速度和位置;

Step6:如果满足设定的阈值或达到最大进化代数，则输出结果，算法结束，否则，跳转到Step2。

4 实验及结果分析

为了验证CCPSO－FCM算法的有效性，我们从复旦大学文本分类语料库中随机选取了体育、军事、房地产、经济以及科技等5个大类，每一类文章选200篇，共1 000篇文献进行实验。在实验前，必须先对所有的文档进行分词、词频统计、特征选择等预处理，最后得到的文本特征向量维数为4 165。实验的硬件配置为酷睿i3CPU 2.8 GHz、4 G内存。软件环境为64位Win7系统，采用Matlab7编程实现。实验所采用的相关参数的值设置如下:模糊指数b=2、最大进化代数Gmax=500，粒子群规模N=20。由于涉及到5类文档，因此本实验中选择的聚类中心数m=5，实验结果采用准确率和召回率这两个评价指标。经过多次运行，取结果最好的一次，如表1所示。

表1 CCPSO－FCM算法的实验结果

从表1可以看到，CCPSO－FCM算法具有较高的准确率和召回率。为了能进一步证明CCPSO－FCM算法的性能，我们把它与PSO－FCM算法和FCM算法在经济类文档上进行了对比实验，结果如表2所示。

表2 三种算法的对比实验结果

从表2中可以看出，没有经过优化的FCM算法性能最差，主要原因在于聚类中心的初始值是随机的，对算法的性能影响很大，经过PSO优化的FCM算法相对FCM算法在性能上有所提升，这主要是因为在聚类中心的初始值经过PSO算法优化后趋于合理。本文提出的CCPSO－FCM算法明显要优于其它两种算法，这主要得益于改进算法设计的振荡环节增加了粒子种群的多样性，同时引入的混沌搜索环节能有效保证粒子群能搜索到局部极值，保证了算法的收敛性。

5 总结

本文提出了基于混沌振荡粒子群优化的模糊C均值聚类方法，该方法在标准PSO算法中设计了一个振荡环节，同时引入混沌理论来进一步增加粒子群的多样性和收敛性。将改进后的PSO算法和FCM算法相互结合，并应用于文本挖掘中。仿真实验表明，相对于PSO－FCM算法和FCM算法，CCPSO－FCM算法具有良好的全局搜索能力和收敛速度，有效提升了传统FCM算法的聚类效果，对文本挖掘算法是一种有益的补充。

［1］刘志勇，耿新青.基于模糊聚类的文本挖掘算法［J］.计算机工程，2009，35(5):45－49.

［2］叶吉祥，林泉.基于粒子群算法的文档模糊均值聚类分析［J］.计算机工程与设计，2009，30(6):1 446－1 448.

［3］徐刚，杨玉群，刘斌斌，等.一种基于多样性策略的粒子群算法［J］.南昌大学学报(理科版)，2013，37(1):17－21.

［4］耿立艳，赵鹏，张占福.基于二阶振荡微粒群最小二乘支持向量机的物流需求预测［J］.计算机应用研究，2012，29(7):2 558－2 560.

［5］胥小波，郑康峰，李丹，等.新的混沌粒子群优化算法［J］.通信学报，2012，33(1):24－30.