一类种群动力学脉冲系统的周期解

侯宗毅，磨峰

(河池学院 数学与统计学院，广西 宜州 546300)

0 引言

近年来，生态数学成为人们研究的热点课题［1－5］。文献［6］讨论了一类种群动力学系统:假设x(t)和y(t)分别表示食饵和种群在时刻t的数量，则食饵—种群系统的动力学行为可由下述方程表示

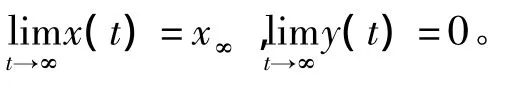
其中0＜α＜1，λ＞0是常数。应用分析的方法，作者研究了系统(1)周期解的存在性。但是，在实际问题中，为了保证种群不至于灭绝而保持一定数量(即系统存在周期解)，食饵的增量不应该是常数，即不应当置种群减少多少都不顾而一味增加常量的食饵，而应该与种群原来的数量(密度)以及原来食饵的数量有关，这有助于避免资源的浪费。为此我们研究下述较之系统(2)更切合实际的脉冲系统:

其中β，λ是常数。在适当的假设条件下，我们得到了保证系统(3)存在周期解的一组充分条件，推广了文献［6］的结果。

1 主要结果

定理1 假设下述条件成立:

(H1)δ，γ，ε均是正常数，0＜α＜1而λ，β是常数。tk是z(t)=(x(t)，y(t))T的第一类间断点，即z(tk)=z()，Δz(tk)=z)－z()。脉冲效应时刻tk是周期序列，即存在正整数q使得tk+q=tk+ω，ti＜ti+1(i=0，1，2，…)。

则系统(3)存在唯一周期解。

证明:假设x=ξ(t)，y=η(t)是(3)的 ω －周期解，记 ξ0=ξ(0+)，η0=η(0+)，ξ1=ξ(ω)，η1=η(ω)，=ξ(ω +)=η(ω +)。由解的 ω 周期性知=ξ0，=η0，并且有

对t∈0，(]ω，系统(3)的解x=ξ(t)，y=η(t)满足关系式

特别当t=ω时，我们有

结合(4)式得η0应满足方程

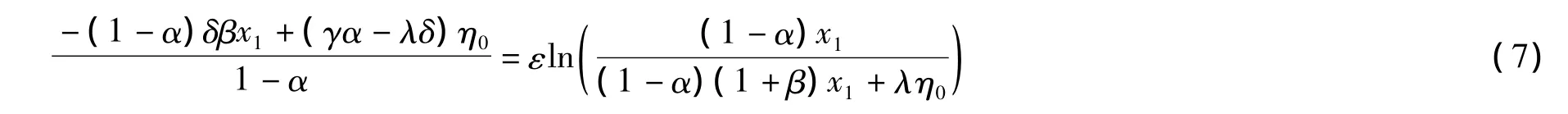
从而在(7)式中当η0取正值时可以得到x1的一个估计值(即脉冲时刻)，因为只要x1的取值满足(7)式就可以了。

现在对系统(3)的解x(t)，y(t)根据文献［6］的定理8.1，要保证x(t)，y(t)确实是系统的ω周期解，需要计算乘子μ的值，使得|μ|≤1。根据文献［6］186页中的公式(8.9)我们有

于是有

本文考虑了在一个ω周期内有一个脉冲点的情形，对一个ω周期内有多个脉冲点的情形将另文给出。由于假设食饵取值与x，y有关，从而未必常数λ一定为正，只要λ满足定理假设条件(2)就可以了，因为此时即便λ取负值而β取适当正值仍然可以保持食饵增量为正。

［1］陈兰荪，宋新宇，陆征一.数学生态模型与研究方法［M］.成都:四川科学技术出版社，2003.

［2］马知恩，周义仓，王稳地，等.传染病动力学的数学建模与研究［M］.北京:科学出版社，2004.

［3］王庚.三种群非线性食饵—捕食反应扩散系统奇摄动Robin问题［J］.纯粹数学与应用数学，2007，23(2):152－156.

［4］刘潇.污染环境中具有脉冲的单种群模型的最优捕获问题［J］.生物数学学报，2007，22(3):265－271.

［5］王政.具非线性饱和功能反应的捕食者—食饵系统的定性分析［J］.生物数学学报，2007，22(2):215－218.

［6］Bainov D，Simeonov P.Impulsive differential equations:periodic solutions and applications［M］.New Youk:Pitman Monographs and Surveys in Pure and Applied Mathematics 66，1993.