论教育投入及其结构对经济增长的作用

2015-03-16卜振兴

西南大学学报（社会科学版） 2015年5期

关键词：财政性教育经费变量

卜振兴

(南开大学经济学院/国家经济战略研究院,天津市300071)

论教育投入及其结构对经济增长的作用

卜振兴

(南开大学经济学院/国家经济战略研究院,天津市300071)

教育投入和教育投入结构是影响经济增长的重要因素,利用我国1990－2012年教育经费投入、高等教育投入占总投入的比重和国内生产总值数据,实证研究了教育投入、投入结构对经济增长的影响.研究表明:教育投入与经济增长正向相关,而教育投入结构(高等教育投入占总投入的比重)与经济增长是负相关关系.因此,国家应进一步加大财政性教育经费的投入,同时在投入方向上向中等和基础教育倾斜.

教育投入;投入结构;经济增长;向量自回归模型;误差修正模型

一、引言

教育投入也称教育投资,是指一个国家或地区在一段时间内投入教育领域中各种资源的总和[1].我国的教育投入如果按照规模来讲,包括财政性教育经费、民办学校中举办者投入、社会捐赠经费、事业收入和其他教育经费投入.教育经费投入如果按照投入教育机构的层级来讲,又分为高等教育投入、中等教育投入和基础教育投入.教育投入的规模决定了教育事业发展的物质基础,教育投入的结构决定了教育经费投入的方向,并间接决定了教育的产出方向.教育投入规模和结构都对经济增长具有重要作用,教育可以促进实业发展,并最终促进经济增长[2].教育可以实现自然与人文优势向经济优势的转变[3],因此重视教育投入及其投入结构对经济增长的影响具有非常重要的意义.为了更好地了解我国教育投入规模和结构的变动和发展情况,我们对1990－2012年教育经费投入情况进行了分析.

我国的教育经费投入由1990年的564亿元增长到了2012年的22 236亿元,年均增长17.22%,增幅快于国民收入增长率.除1991年、1998年外,其余年份的教育经费投入增长率均保持两位数以上,尤其是2006－2012年,增长率达到20%左右.教育经费投入占GDP的比重也是衡量教育规模的一个重要指标.我国1990－2012年教育经费占GDP的比重平均为2.94%,整体呈现震荡上升的趋势.2012年教育经费投入占GDP的比重达到4.28%,首次突破4%的水平.但是这一指标与一些教育发达国家仍存在很大的差距.例如根据世界银行的统计数据,早在2000年的时候,丹麦的教育经费占GDP的比重就已经达到8.3%,加拿大为5.6%,法国为5.7%,瑞典为7.2%,英国为4.5%.因此,我国的教育经费投入还有进一步提升的空间.

高等教育经费投入占总经费投入的比重是衡量教育投入结构的重要指标.通过对1990年－2012年的数据分析,我们可以发现:一是1990－2012年高等教育经费投入占比一直处于14%以上;二是根据高等教育经费投入占总教育经费投入比重的变动情况,可以将我国的教育投入结构划分为以下阶段:1990－1992年为高等教育经费投入占比上升阶段,1992－1995年为下降阶段,1995－2003年为上升阶段(其中主要受高校扩招的影响),2003－2009年为下降阶段(高校扩招幅度放缓、国家加大对基础教育和中等教育的投入),2009－2012年为快速上升阶段.这几个阶段反映了国家对于高等教育投入的重视情况.

教育投入会提升人力资本,而教育投入结构决定了人力资本提升的方向.根据内生经济增长理论的观点,人力资本提升会促进经济的增长.这种情况在中国是否适用,教育投入和投入结构在经济增长中各起到什么作用,这是本文需要解决的问题.在我国不断重视教育发展,加大高等教育投入的背景下,给予上述问题明确的回答不仅具有理论意义也具有现实意义.

二、文献回顾

本文的研究重点主要在教育经费投入和高等教育投入占总投入的比重对经济增长的作用,因此文献回顾主要从教育投入和高等教育投入对经济增长的影响展开.

(一)教育投入与经济增长

根据人力资本理论,教育投入越高,人力资本越大,因此经济增长越快.所以教育投入与经济增长是正相关关系[4].Ganegodage和Rambaldi[5]以新古典增长理论和内生经济增长理论为基础,研究了斯里兰卡1959－2008年教育投入对经济增长的影响,研究表明教育投入与经济增长是正相关关系.Razak et al[6]基于马来西亚1970－2010年的数据,利用向量自回归模型研究了财政性教育经费投入与经济增长之间的关系,除了考虑高等教育投入外还考察了固定资本投资、劳动力数量等因素,研究表明经济增长与选取变量之间呈现正向相关系,教育等人力资本因素在马来西亚的经济增长中发挥重要的作用.Ghosh Dastidar et al[7]通过理论模型和实证分析研究了印度公共教育投入与经济增长之间的关系,研究表明,教育投入是否对经济增长产生促进作用取决于经济制度和劳动力市场,同样也取决于贸易开放度等其他因素.正是由于以上因素的存在,印度公共教育投入与经济增长之间的关系缺少一致性.

国内关于教育投入与经济增长的研究也有很多,如于凌云[8]以卢卡斯的人力资本理论为模型,利用1996－2005年我国31个省级单位的面板数据,研究了非政府教育经费投入和财政性教育经费投入对经济增长的影响,研究表明教育投入对经济增长具有短期效应,相较于财政性教育投入,非财政性教育投入对人力资本积累产生了更大的促进作用.肖小虹[9]以人力资本理论和内生经济增长理论为基础,选取了1953－2008年贵州教育投入与经济增长的数据,运用协整检验和因果关系检验研究了教育投入与经济增长的关系,研究表明两者之间长期存在稳定的均衡关系,教育投入每增加1个百分点,经济增长增加0.70个百分点,但是由于教育投入的滞后性,经济增长先促进了教育投入的增加,七年后教育投入对经济增长的促进作用才逐步显现.

(二)高等教育投入与经济增长

Gyimah-Brempong et al.[10]利用1960－2000年亚洲国家的面板数据,研究了高等教育人力资本对经济增长的作用.研究表明不同水平的人力资本都对人均收入的增长产生了显著的正向作用,并且高等教育人力资本增长对经济的拉动作用,大概是物质资本作用的两倍.Bradley[11]利用美国1970－2005年的面板数据,在考虑了非政府性教育投入的因素后,研究了高等教育财政性投入与经济增长之间的关系,研究发现,在一个私立教育机构就读的学生份额占比较大的州,高等教育财政性支出对经济增长具有促进作用,但是在私立教育机构就读的学生份额占比较低的州,两者之间呈现负相关关系.

赵树宽等[12]利用我国1990－2008年的数据,通过向量自回归模型研究了高等教育投入对经济增长的影响.研究表明高等教育经费投入与经济增长之间存在长期均衡关系,高等教育经费投入每增加1个百分点,经济增长增加0.251个百分点.邓水兰等[13]选取了江西省1995－2011年经济增长、高等教育经费投入和师生人数比三个变量,研究了高等教育投入和人员投入对经济增长的促进作用.通过回归检验表明高等教育投入对经济增长产生了促进作用,但是作用时间不长,同时经济增长也对教育投入产生了促进作用.

总结近年来的文献,我们发现,在教育经费支出促进经济增长方面,学者们基本取得了共识,但是对于财政性高等教育经费投入对经济增长是拉动还是抑制却没有形成共识.另外,国内外大量的相关文献主要集中于教育经费投入或高等教育经费投入与经济增长的关系研究,并没有关于教育经费投入结构的相关研究.与以往的研究相比,本文的不同之处在于:一是在考察教育经费投入规模的同时,引入了教育经费投入结构这一核心变量;二是在考察核心变量的同时,将金融发展、经济开放度、财政支出规模、城市化率等影响经济增长的关键指标引入经济增长核算模型,使估计结果的误差进一步降低;三是利用了我国1990－2012年的数据,该数据反映了中国财政性教育经费投入和高等教育投入占比的最新动向,检验更有实践意义.总之,本文加深了对于财政性教育经费投入规模、教育投入结构与经济增长关系的认识,为中国教育经费的投入及投入方向提供了一定的借鉴参考.

三、模型设定和数据说明

在模型中,gdp表示国民收入,edu表示高等教育投入,edus表示教育投入结构,a0表示常数项,ai表示系数,Xt表示参考变量,可能影响经济增长的参考变量包括居民消费(con)、企业投资(inv)、金融发展(fd)、经济开放度(eo)、财政支出规模(gov)、城市化率(urb)、失业率(unr)及基尼系数(gini).

(二)模型设定和数据说明

1.参数设定

本文的参数设定,参照经典的指标表示方法,其中国民收入用国民生产总值表示,这是表示国民收入最重要的指标之一;教育经费投入主要指国家财政性教育经费投入;居民消费用社会消费品零售总额表示,它可以反映社会商品购买力的实现程度,居民消费是拉动经济增长的主要引擎[14];企业投资用固定资产投资总额表示,反映了企业等私人部门进行生产和运营的基本建设资金投入,固定资产投资对于经济增长的促进作用由固定资产投资的种类决定[15];金融发展用商业银行存款余额表示,它反映了虚拟经济的规模大小,金融发展会对经济增长产生促进作用[16];经济开放度等于对外贸易总额/国内生产总值,它反映了一个国家对外贸易和开放的程度,经济开放可以实现对资源和要素的优化配置,一般会促进经济的增长(Romer,1986、Lucas,1988);财政支出规模,等于财政支出总额/国内生产总值,表示了政府主动刺激经济增长作用的大小,关于财政支出规模对经济增长的影响作用存在较大争议(Lucas,1985、Barro,1990等);城市化等于城市人口占总人口的比重,城市化会促进消费,同时也会带动基础设施建设等,从而促进经济增长[17];失业率是指失业人口在全部劳动力人口中的比重,根据奥肯定律的解释,失业会造成人力资源投入的浪费,不利于经

(一)理论假设

本文的基准模型参照经典的国民收入核算理论模型,同时在模型中加入所需要研究的变量,因此模型设定如下:济实现充分就业的增长[18];基尼系数是判断收入分配公平性的重要指标,基尼系数越低表示收入分配差距越小,基尼系数越高表示收入分配差距越大,根据Kuznets[19]提出的倒“U”型假说,经济增长与收入差距之间呈现倒“U”型关系.

2.相关性分析

为了消除变量的波动性以及由此带来的异方差的问题,同时也为了使单位统一化,更好地揭示变量之间的关系,我们对其中的绝对变量(如gdp、edu、con、inv等)取对数,然后以lngdp为控制变量,进行相关性检验,以避免回归结果出现多重共线性的问题.相关性检验表明:消费总额lncon、金融发展fd、政府支出规模gov、城市化率urb、基尼系数gini与其他指标相关性较高,为了消除多重共线性,将相关性较高的指标进行删除,删除后的指标为高等教育投入lnedu、高等教育投入结构edus、政府投资lninv、经济开放度eo和失业率unr.再进行相关性检验,检验结果表明变量之间的相关系数均小于0.6,可以认为不存在显著的相关性.

3.模型设定

在进行相关性检验,删除相关性较高的指标变量后,我们的模型精简为:

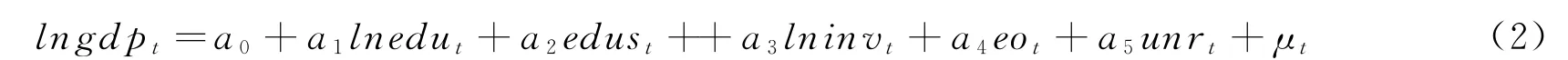
其中,lngdp表示对数化的国民收入,lnedu表示对数化的教育经费投入,edus表示教育投入结构,lninv表示对数化的投资,eo表示经济开放度,unr表示失业率,ai(i＝1,2,…,5)表示系数,μ表示残差项.各变量的相关图如下所示:

从图1我们可以发现,lngdp变量与其他变量之间呈现近似的线性相关关系,模型设定是较为合理的.

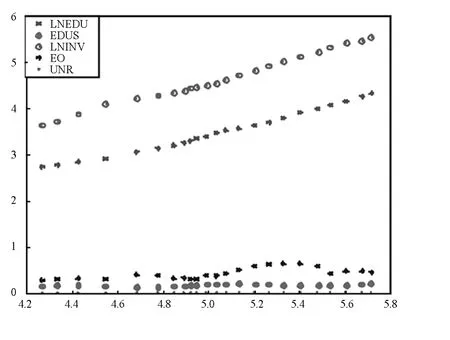
图1 变量相关图

(三)数据来源

本文教育经费投入及教育投入结构数据来源于《中国教育统计年鉴》(1991－2013)和《中国教育经费统计年鉴》(1991－2013)、《中国教育事业发展统计公报》(1991－2013),并经计算整理而得;国民收入gdp、居民消费con、固定资产投资inv、经济开放度eo、财政支出规模gov等宏观经济数据来自《中国统计年鉴》(1991－2013),并经计算整理而得;城市化率来自于《中国统计年鉴》(1991－2013),城镇居民登记失业率数据来自于《中国人口和就业统计年鉴》(1991－2013);由于国家并未给出1990－2003年官方的基尼系数,因此我们采用各年《中国统计年鉴》、《中国统计摘要》,并借鉴贺晋,李玲玲(2012)[20]的数据整理而得.

四、模型检验和结果说明

(一)平稳性检验

Granger(1974)提出对非平稳变量不能进行简单的OLS估计,因为这会使弃真的概率大大增加,从而造成伪回归.为了避免这种情况,我们首先必须对变量进行平稳性检验,以确定采用合适的估计方法,提高估计结果的有效性和无偏性.平稳性检验的方法包括:直接观察法、相关图法、单位根检验等方法.其中单位根检验是较为定量和客观的方法,本文就采用这种方法.

单位根检验的方法中最常用的是ADF检验和PP检验.为了确保估计结果的稳健性,本文采用这两种办法对选取的变量进行单位根检验.检验结果表明,在5%的显著性水平下,选取变量均为非平稳变量,经过一阶差分后,单位根检验的统计量小于临界值,落在了拒绝域,拒绝了存在单位根的原假设.因此国民生产总值(lngdp)、教育投入(lnedu)、教育投入结构(edus)、政府投资(lninv)、经济开放度(eo)和失业率(unr)均为一阶单整I(1)过程.

(二)向量自回归分析

传统的经济计量方法是以经济理论为基础来描述变量关系的模型,但是经济理论通常并不能对变量之间的动态关系进行严密的说明.为了解决这一问题,Christopher Sims[21]提出了向量自回归模型(vector auto regression,VAR)和向量误差修正模型(vector error correction model,VEC)来研究变量之间的关系,目前已经被广泛运用于宏观经济变量的分析中.VAR模型是用模型中所有当期变量对所有变量的若干滞后变量进行回归,从而估计全部内生变量的动态关系.

1.模型特征根

建立VAR模型首先要满足平稳性的假定,平稳性要求通用特征方程的特征根均要位于单位圆以内,稳定性检验结果如下:

图2 原变量稳定性检验

图3 一阶差分后稳定性检验

由稳定性检验可知原变量的单位根有一个位于单位圆之外,不满足稳定性的要求,差分后的特征根均位于单位圆内,表明差分后的模型满足稳定性要求,可以进行脉冲、方差分解等计算.

2.脉冲响应

由于VAR模型的估计结果只具有一致性,单个参数估计值的经济解释是很困难的.要想对一个VAR模型做出分析,通常是观察系统的脉冲响应函数和方差分解.脉冲响应函数解释了变量是如何对各种冲击做出反映的,以及反映的程度.具体地说,它描述的是在随机误差项上施加一个标准差大小的冲击后对内生变量的当期值和未来值所带来的影响.为了避免var模型误差项相分析带来的困难,很多学者采取了cholesky分解方法,对误差项进行正交化处理,但是这种方法对分解顺序的要求较高,不同的分解顺序会产生不同的分析结果,为了降低正交化处理对于分解顺序的依赖性,pesaran和Shin(1988)提出了一般脉冲响应分析(generalized impulse response)方法,本文就是基于这一方法.经济增长对各种变量冲击的响应如下图所示:

图4 d(lngdp)对自身冲击的响应

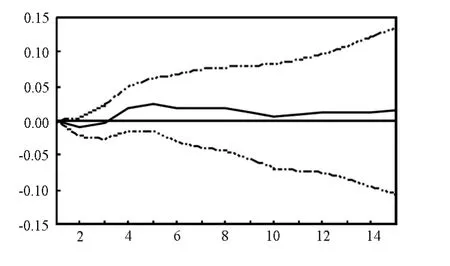
图5 d(lngdp)对d(lnedu)冲击的响应

图6 d(lngdp)对d(edus)冲击的响应

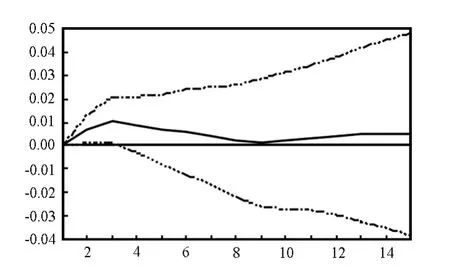
图7 d(lngdp)对d(lninv)冲击的响应

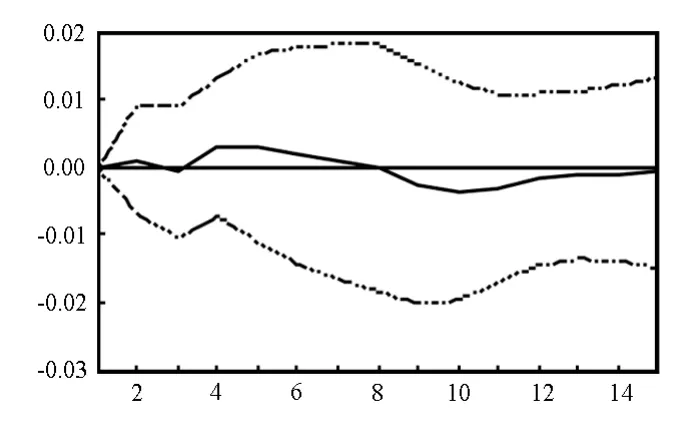
图8 d(lngdp)对d(eo)冲击的响应

图9 d(lngdp)对d(unr)冲击的响应

如上图所示,在一个单位的冲击下,gdp对于自身的冲击初始值较高,在第五年后基本消失; gdp对教育经费投入的冲击在第三年才开始响应,直至第十年响应基本结束;gdp对教育经费投入结构的冲击在第四年才开始响应,并在第十年基本消失;gdp对固定资产投资冲击的响应一开始就发生,冲击的影响在第八年基本消失;gdp对经济开放度和失业率的响应很小,基本没有产生明显的影响.

相对于其他冲击因素的影响,教育经费投入和教育投入结构的冲击表现出三个特点:一是冲击不是当期发生,一般会延迟几期对经济增长的冲击作用才会显现;二是冲击作用较为明显,尤其是与经济开放度和失业率相比;三是冲击持续时间较长,一次冲击发生基本要持续6期左右的时间,6期后影响才会基本消失.

3.方差分解

方差分解反映了未来预测误差由不同信息的冲击影响的比例或贡献的百分比决定,对d(lngdp)的分解如下所示:

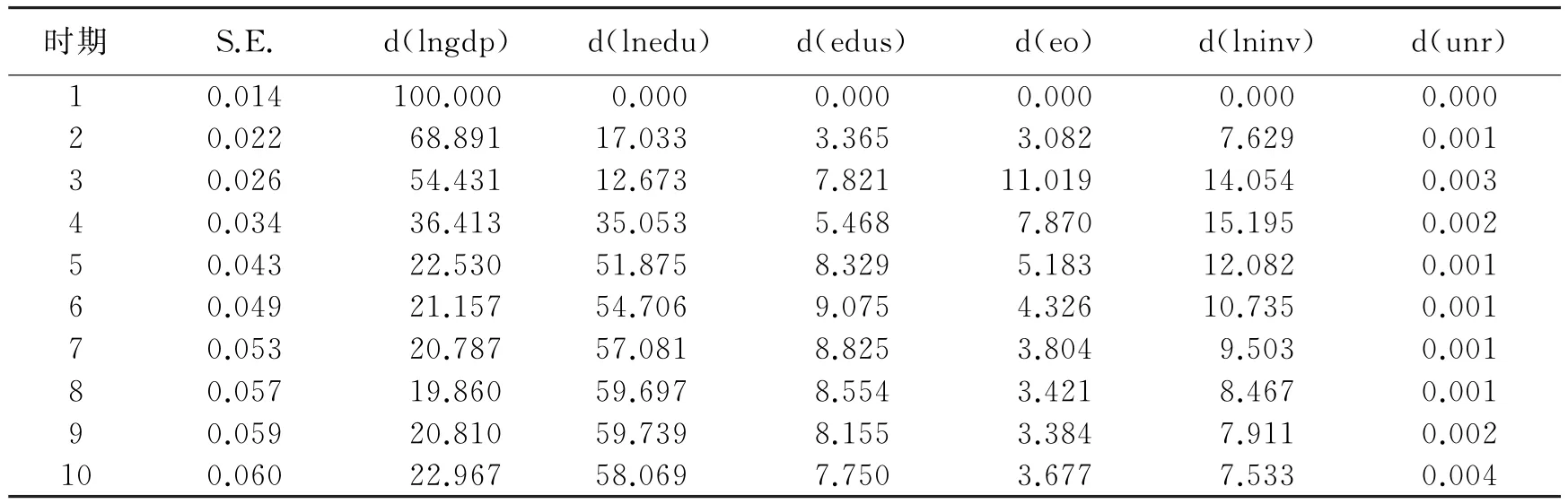
表2 d(lngdp)的方差分解结果表(%)

方差分解的结果表明:d(lngdp)自身的滞后影响从第一期的100%迅速下降到第五期的22.5%,之后基本维持在23%的水平之上,这说明d(lngdp)惯性较小,呈现较低的粘性度,如果没有其他因素的影响,经济增长很难长期维持;教育经费投入d(lnedu)对于经济增长的影响在第一期后呈现快速上升的趋势,在第五期达到51.9%,之后进入平稳上升阶段,并基本维持在59%左右的水平;教育投入结构对经济增长的滞后影响在第一期到第六期出现小幅震荡,以后各期基本维持在7%左右的水平;经济开放度、固定资产投资对经济增长的滞后影响趋势相似,基本在前几期出现小幅震荡,之后基本维持在较低的水平上,其中经济开放度为5%左右,固定资产投资为6%左右;失业率对经济增长的冲击影响较小.

总结起来,教育投入和经济增长自身因素的滞后影响是经济增长冲击的关键变量,其余变量的影响均较低.

(三)协整关系检验

协整是对非平稳变量长期均衡关系的统计描述.单个变量是非平稳的,但是两个非平稳变量之间往往存在稳定的均衡关系,下面本文就对lngdp、lnedu、edus、lninv、eo和unr是否存在长期均衡关系进行检验,检验公式如下:

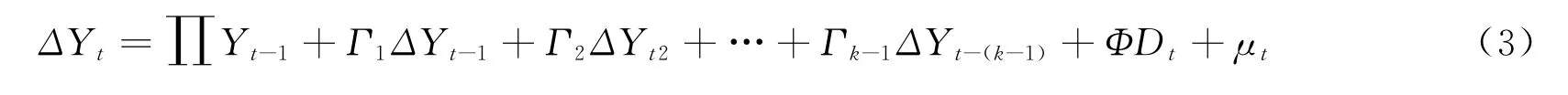
对于协整关系的检验方法主要有两种:迹检验和最大特征值检验,本文采取了迹检验的方法,检验结果如下表所示:

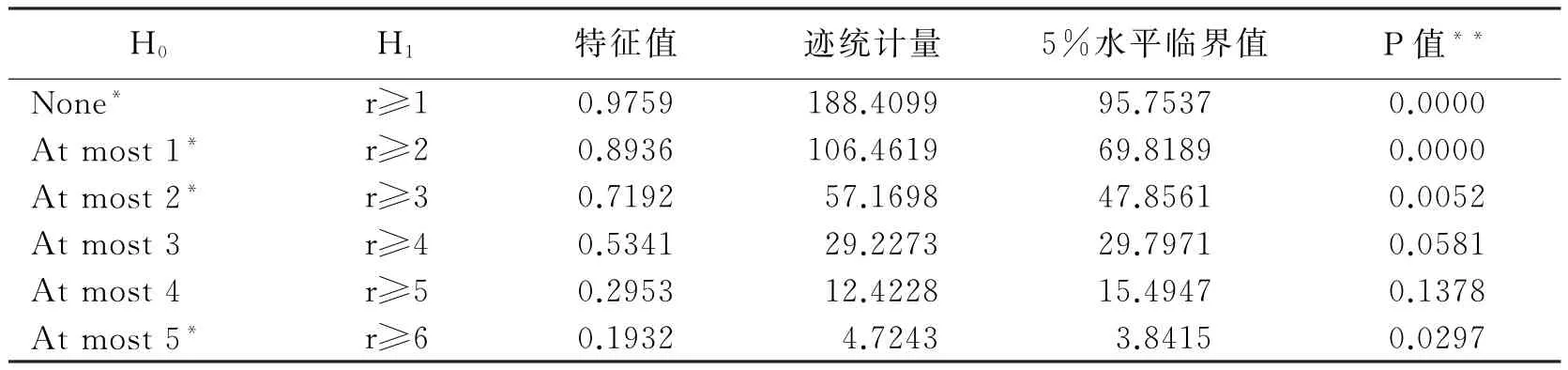
表2 协整向量个数r迹统计量检验

迹统计量检验:因为57.1698＞47.8561,所以拒绝原假设“At most 2(至多存在两个协整关系)”,同时29.2273＜29.7971,接受原假设“at most3(存在三个协整关系)”,检验结果表明经济增长、教育经费投入、教育投入结构、经济开放度、固定资产投资和失业率之间存在三个协整关系.

(四)格兰杰非因果关系检验

协整检验表明:教育经费投入和教育投入结构与经济增长之间存在长期的均衡关系,下面运用格兰杰(Granger,1969)提出的非因果性检验进一步验证三者之间的关系.格兰杰非因果性检验指的是,若加上xt的滞后变量后对yt的预测精度不存在显著性改善,则称xt－1对yt存在格兰杰非因果性关系,为简便,通常总是把xt－1对yt存在非因果关系表述为xt对yt存在非因果关系(严格讲,这种表述是不正确的).

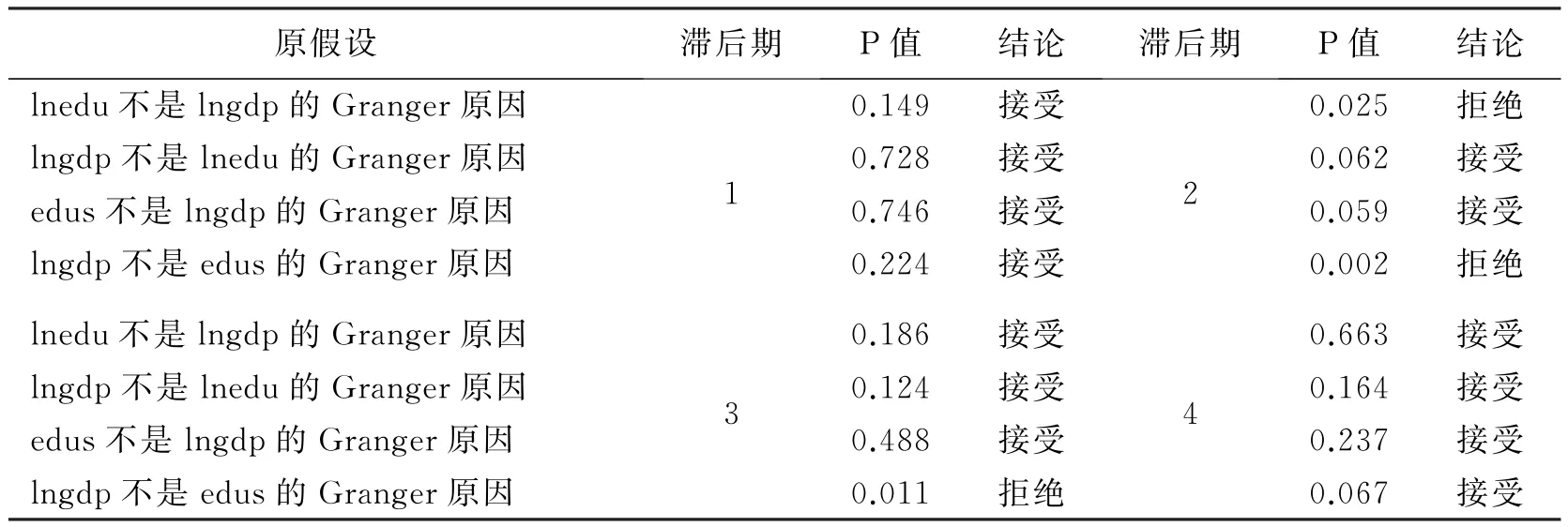
表4 格兰杰因果检验表

检验结果表明:滞后期为1期时,lnedu、edus和lngdp之间不存在格兰杰因果关系;当滞后期为2期时,教育经费投入是经济增长的格兰杰因果关系,经济增长是教育经费投入结构的因果关系;滞后期为3期时教育经费投入对经济增长的作用并不明显;滞后期为4期时经济增长对教育经费投入结构的因果关系也不显著.

(五)误差修正模型

如果变量是一阶单整,同时又存在长期均衡关系,那么这些非平稳变量的线性组合则是平稳的,此时如果建立差分var模型将会丢失重要的非均衡误差信息,为了解决这一问题,格兰杰提出了向量误差修正模型.当有一个大范围的短期动态波动时,VEC表达式会限制内生变量的长期行为收敛于它们的协整关系.因为一系列的部分短期调整可以修正长期均衡的偏离,所以协整项被称为是误差修正项.根据协整向量个数检验结果表明,研究变量之间存在三个协整关系,因此进入VEC模型的误差修正项分别是:

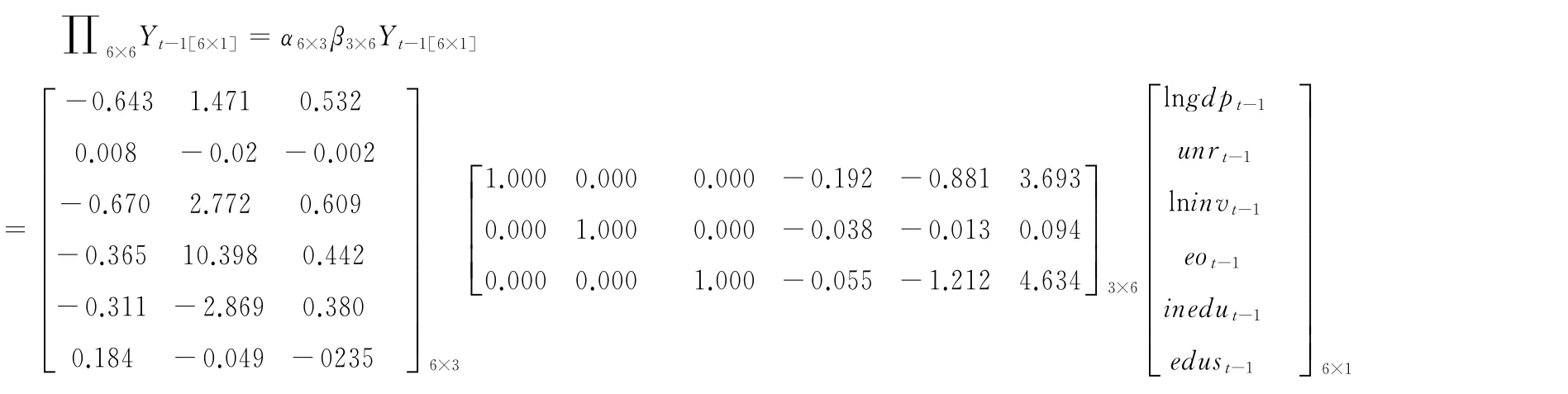
因此变量之间的长期关系为:

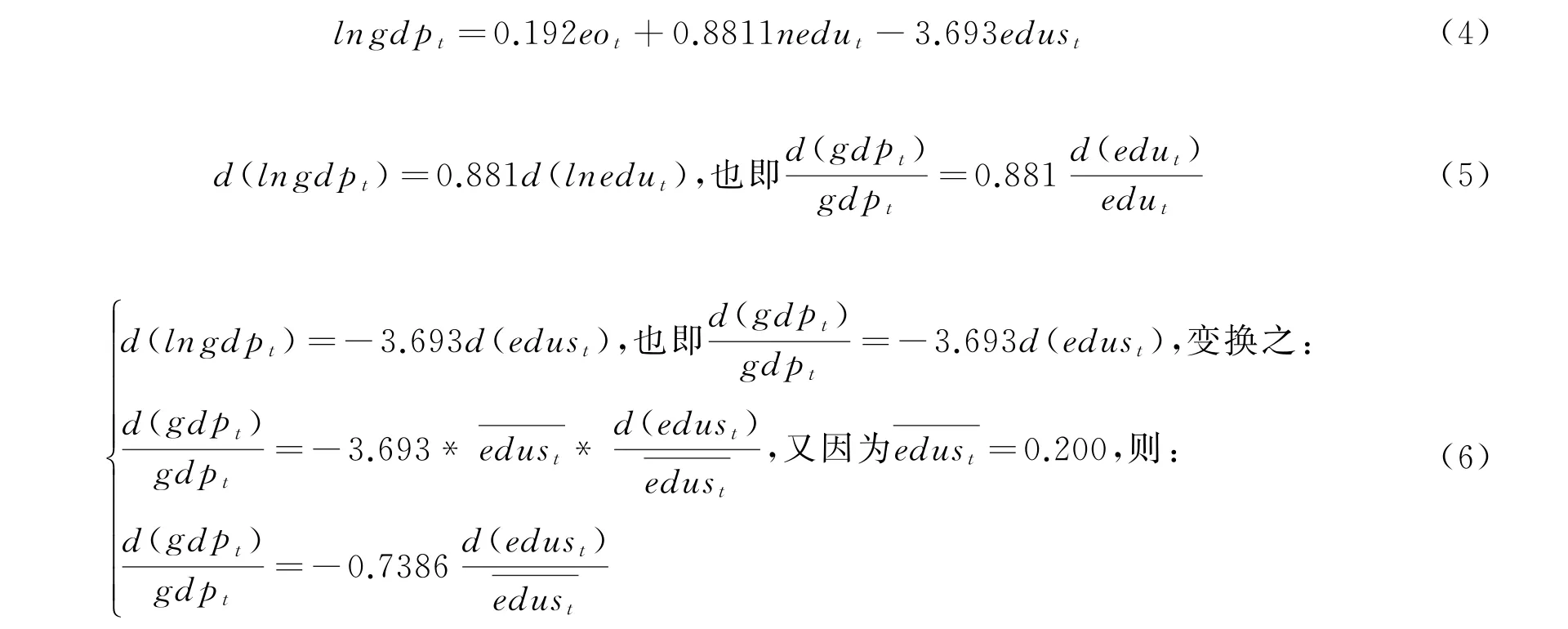
由误差修正模型可知:教育投入与经济增长的弹性为0.881,即教育投入每增加1个百分点,国民收入增长0.881个百分点,教育经费投入对经济增长的促进作用还是较为明显的;教育投入结构与经济增长的弹性为－0.7386,即教育结构(高等教育投入在教育经费投入中的比重)每上升1个百分点,国民收入下降0.7386个百分点,这说明我国当前的财政性教育经费对高等教育的投入比例相对于初等教育和中等教育偏高.当前,在保持高等教育投入适当规模的前提下,财政性教育经费应更多地支持中等和初等教育的发展.

五、结语

随着国家对创新能力和创新人才的关注,教育被提升到了非常重要的位置.国家每年也安排一定比例的财政资金用于教育事业的发展,有力地提升了我国的教育水平和人力资源水平.按照新经济增长理论的观点,人力资本的提升会带动经济的增长,那么财政性教育经费投入的规模和投入方向在经济增长中到底发挥了多大的作用?在教育投入力度逐步加强和教育改革不断深入的背景下,回答上述问题有非常重要的现实意义.

为此,本文基于1990－2012年的教育投入、教育投入结构和经济增长等相关变量的数据,采用向量自回归模型和误差修正模型分析了我国教育经费投入及其结构对经济增长的影响.通过检验我们有以下结论:第一,教育经费投入及其结构对经济增长的冲击影响较为显著,但是发生作用有一定的延迟,这与固定资产投资等变量对经济增长快速响应有明显的区别;第二,教育经费投入在解释经济增长的预测误差方面占有较大比重,同时教育经费投入是经济增长的格兰杰因果关系;第三,经济增长、教育经费投入及结构之间存在协整关系,三者之间的长期均衡关系表明教育经费投入与经济增长呈正相关关系,弹性为0.881,而教育经费投入结构(即高等教育投入占总投入的比重)与经济增长之间是负相关关系,高等教育经费投入占比每增加一个百分点,国民收入下降0.7386个百分点.

因此,为了更好地发挥教育对经济增长的推动作用,一方面要继续加大财政资金对于教育的支持力度,另一方面由于高等教育投入占比与经济增长是负相关关系,而在财政性教育经费投入一定的情况下,高等教育投入占比与初等教育和中等教育比是此消彼长的关系,所以在财政性教育经费的分配中应该向中等教育和初等教育倾斜,以充分发挥财政性教育经费投入对经济增长的拉动作用.

[1]刘道兴.教育投入的革命[M].北京:社会科学文献出版社,2011:11-15.

[2]李忠.近代中国“教育救国”与“实业救国”的互动[J].西南大学学报:社会科学版,2011,37(4):141-148.

[3]张学敏,史利平.文化－教育－经济共生机制:西南民族地区教育反贫困战略选择[J].西南大学学报:社会科学版,2012,38(6):48-53.

[4]Schultz T.Investment in Human Capital[J].American Economic Review,1961,3(151):1-17.

[5]Ganegodage K R,Rambaldi A N.The impact of education investment on Sri Lankan economic growth[J].Economics of Education Review,2011,30(6):1491-1502.

[6]Razak M Y M H,Muhammad F,Hussin M F A,et al.Education Expenditure and Economic Growth A Causal Analysis for Malaysia[J].Journal of Economics and Sustainable Development,2012(3):7.

[7]Ghosh Dastidar,Sayantan,Sushil Mohan,et al.The relationship between public education expenditure and economic growth:The case of India[J].2013:1-15.

[8]于凌云.教育投入比与地区经济增长差异[J].经济研究,2008(10):131-143.

[9]肖小虹.贵州经济增长与教育投入的实证分析[J].财经问题研究,2010(8):119-122.

[10]Gyimah-Brempong K,Paddison O,Mitiku W.Higher education and economic growth in Africa[J].The Journal of Development Studies,2006,42(3):509-529.

[11]Bradley R.Curs B C S.The Roles of Public Higher Education Expenditure and the Privatization of the Higher Education on U.S.States Economic Growth[J].Journal of Education Finance,2011,36(4):424-441.

[12]赵树宽,余海晴,刘战礼.高等教育投入与经济增长关系的理论模型及实证研究[J].中国高教研究,2011(9):11-15.

[13]邓水兰,肖梦露,温诒忠.高等教育投入促进经济增长的实证研究——来自江西省的数据[J].教育学术月刊,2013(10):68-71.

[14]江小涓.大国双引擎增长模式——中国经济增长中的内需和外需[J].管理世界,2010(6):1-7.

[15]Madsen J B.The causality between investment and economic growth[J].Economics Letters,2002,74(2):157-163.

[16]谈儒勇.中国金融发展和经济增长关系的实证研究[J].经济研究,1999(10):53-61.

[17]Moomaw R L,Shatter A M.Urbanization and Economic Development:A Bias toward Large Cities?[J].Journal of Urban Economics,1996(1):13-37.

[18]Okun A M.Potential GNP:its measurement and significance[M].yale university,State of Connecticut,1963:98-103.

[19]Kuznets S.Economic growth and income inequality[J].American Economic Review,1955,45(1):1-28.

[20]贺晋,李玲玲.我国居民消费需求为何不足?——基于1978—2008年基尼系数的分析[J].财经问题研究,2012(6):110-115.

[21]Sims C A.Comparison of Interwar and Postwar Business Cycles:Monetarism Reconsidered[J].American Economic Review, 1980,(2):250-257.

责任编辑曹莉

G40-054