水空跨越航行器密度对出水的影响

余宗金, 冯金富, 徐保伟

(空军工程大学 航空航天工程学院, 陕西 西安 710038)

水空跨越航行器密度对出水的影响

余宗金, 冯金富, 徐保伟

(空军工程大学 航空航天工程学院, 陕西 西安 710038)

为了模拟水空跨越航行器的出水过程并研究其密度对出水过程的影响,结合理想流体与粘性流体对航行器的作用,考虑出水过程中浮力、浮心等物理量的变化以及附加质量的变化率,建立了圆柱航行器斜出水动力学模型,计算了不同密度航行器成功出水的临界速度和临界推力。最后分析得到了航行器密度和出水临界速度与临界推力之间的关系。

密度; 动力学模型; 出水; 临界速度; 临界推力

0 引言

水空跨越航行器是一种能够在水和空气中循环飞行的新概念航行器,针对出水过程的研究是实现水空跨越航行器的关键。航行器的出水过程非常复杂,由于是从水下运动到空气中,所以必然存在流场环境的剧烈变化,会带来一系列复杂的伴随现象,如空泡、出水瞬间的剧烈冲击等,必须采取相应的简化措施。针对航行器出水过程的研究多采用理论模型与数值计算相结合的方法来进行。

有关物体出水的研究,Karman等[1]于1927年提出了计算物体出入水过程中与水面撞击载荷的理论模型,这个经典的基于动量定理的理论模型一直被沿用至今。文献[2]通过实验和有限元理论模型相结合的方法,研究了某种潜射导弹复合圆顶弹头在出水过程中的强度和稳定性。国内针对航行器出水过程的研究也已经有大量的成果,由于计算机技术的迅猛发展,结合各种计算机软件对出水过程的研究已经成为研究物体出水过程的重要方法。文献[3]利用Creator和Vega软件视景仿真的结构特点,对水空跨越航行器的出入水以及水下的航行过程进行了仿真研究模拟。文献[4]利用Fluent软件及其VOF模型,通过数值模拟的方法对结构物出水过程中受到的流体力和顶部压力进行了计算和分析。针对影响航行器出水过程的影响因素,文献[5]利用均质多项流模型和空化模型,对多种头部形状和出水迎角对航行器出水过程流场的影响进行了研究。

为了对水空跨越航行器的出水过程进行模拟研究,并且探究航行器密度对出水过程的影响,本文基于鱼雷水下航行动力学模型和导弹空中飞行动力学模型,充分考虑出水过程中浮力、浮心、质心等物理因素的变化,同时引入了附加质量变化率的概念,建立了航行器斜出水的圆柱体斜出水动力学模型。利用所建立的模型,对不同密度航行器成功出水所需要的临界速度和临界推力进行了模拟和仿真计算,分析了航行器密度与成功出水的临界速度、临界推力的关系。

1 构建模型

1.1 物理模型

建立的物理模型如图1所示,为一个30°尖头的回转圆柱体,全长5.33 m。根据物理模型的数值特征可以得到其外形的具体计算公式R(x)。

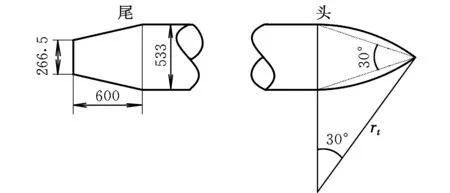
图1 物理模型示意图Fig.1 Shape of the vehicle

圆柱航行器在出水过程中,受到重力G、浮力B、推力T和流体作用力F的相互作用,受力如图2所示。图中以圆柱航行器体轴为x轴,且指向前方为正;y轴垂直于x轴,指向上方为正;z轴垂直于xOy平面,方向使坐标系满足右手系规定。由于航行器在跨越水和空气的自由交界面时,航行器受到的水的作用力F也随着时间在不断变化,变化过程中的F非常复杂,为了便于分析,分别考虑理想流体和粘性流体对航行器的作用效果。

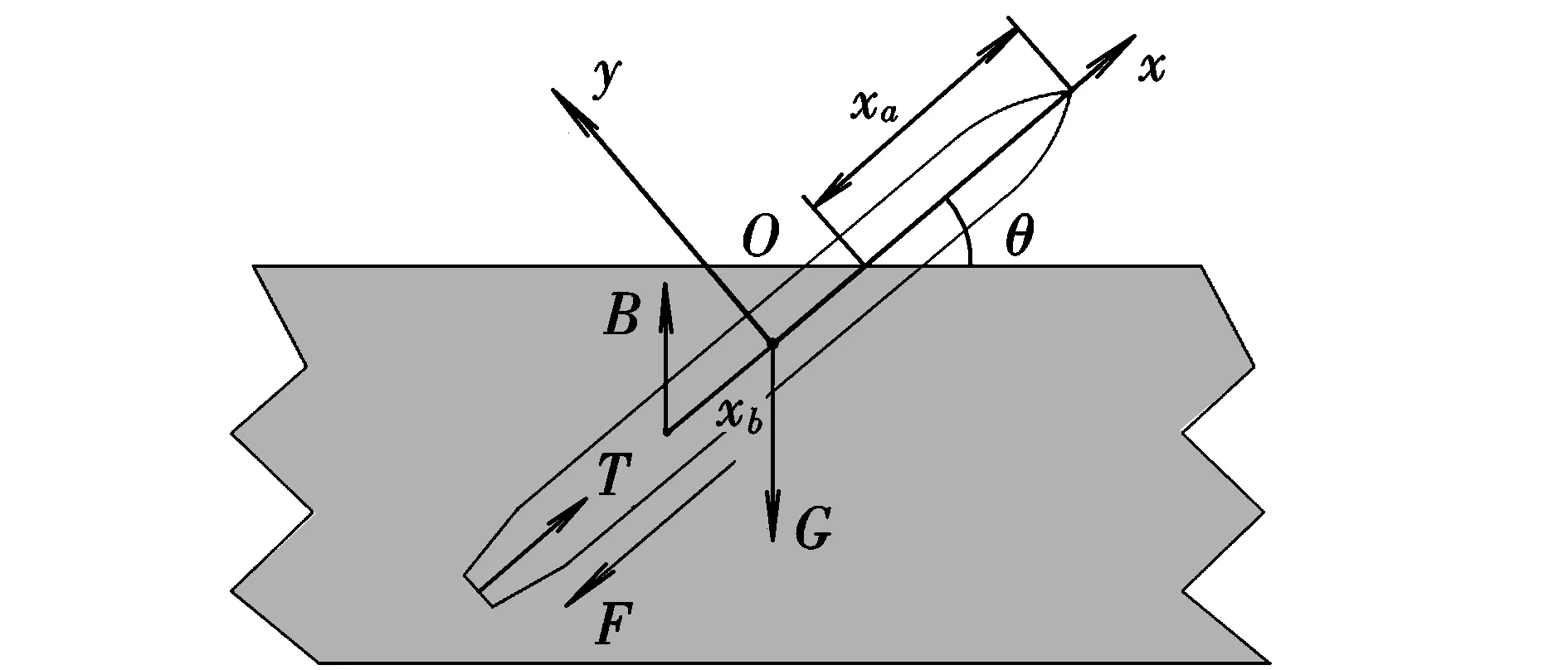
图2 航行器出水过程受力示意图Fig.2 Force analysis of vehicle in the process of water-exit

(1)理想流体作用效果

航行器在理想流体中的受力模型及所建立的动力学模型,只考虑了圆柱航行器在垂直平面内的二维受力情况,再结合模型轴对称的特征,可得到理想流体条件下航行器受到的力和力矩的方程[6]：

(1)

式中:Rix,Riy分别为理想流体对航行器在x轴和y轴方向的作用力;Miz为理想流体对航行器在z轴方向的力矩;λ为附加质量;vx,vy为航行器在x轴和y轴的速度分量;ωz为航行器绕z轴转动的角速度。

(2)粘性流体作用效果

粘性流体作用效果主要包括航行器的运动阻力、升力和由迎角引起的作用力。由于本文航行器是轴对称的,因此不存在运动升力。航行器受到的运动阻力和由迎角引起的作用效果可体现于航行器在水中运动的阻力系数上。实验和实际理论分析指出:水下物体运动的阻力系数与速度、雷诺数和迎角有关[7]。由于本文所采用的速度比较小,所以忽略了雷诺数的影响。航行器的粘性系数计算公式为:

Cx=Cx0(v)(1+kδ2)

(2)

通过数值计算方法可求出航行器模型零迎角阻力系数Cx0(v)和系数k。Cx0(v)在航行器以低速出水时,可以认为是一个常数Cx0,因而有:

Cx=Cx0(1+kδ2)

(3)

阻力方程为:

Fμ=Cx·0.5ρSv2

(4)

粘性流体和迎角引起的作用力和力矩为:

(5)

式中:ρ为水的密度;S为航行器浸水面积;v为航行器运动速度;Rμx为由流体粘性引起的阻力;Rμy为由航行器迎角引起的升力;Mμz为由航行器迎角引起的俯仰力矩;α为航行器迎角;xa为航行器出水过程中露出水面的长度。

1.2 相关参量求解

(1)附加质量及其变化率

随着航行器的出水运动,其浸没水中的体积逐渐减小,附加质量λ也随着逐渐减小,可采用剖面法进行附加质量的计算[8]。计算公式如下:

(6)

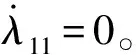
(7)

式中:dxa为航行器头部出水部分长度的变化率。

根据图2物理模型的几何特征可得:

(8)

式中:hf为质心(航行器全浸水时的浮心)距水面的垂直距离,设定其在水面下为负,水面上为正;x0为航行器尾部至质心的距离,为一常量;θ为航行器倾斜角度。

(2)其他参量

浮力B、质心x0、浮心xb0、浮心和质心距离xb、浸水面积S、体积V、转动惯量J的计算公式分别为:

(9)

(10)

(11)

xb=x0-xb0

(12)

(13)

(14)

(15)

1.3 动力学模型构建

根据上述受力分析,构建航行器出水运动动力学模型计算公式为:

(16)

另有辅助公式:

(17)

式(1)～式(17)构成了可描述航行器出水运动的微分方程组,给定初值条件可进行求解。初值条件包括初始速度(vx0,vy0)、初始出水倾斜角θ0、转动角速度ωz0和初始航行器头部顶点在轴线方向距水面的距离xa0,并规定当航行器头部顶点在水下时xa为负值,在水面以上时为正值。

2 航行器密度对出水的影响

2.1 临界出水状态

在进行密度对水空跨越航行器出水所需的速度和推力的研究过程中,选定航行器刚好能够成功出水,即航行器全部脱离水面,自身体轴与水平面平行的状态为航行器出水的临界状态。航行器从其前端距离水面为xa0的初始状态,到最后达到出水临界状态所需要的推力值和速度值称为航行器的出水临界速度和临界推力。由于篇幅有限,本文仅讨论航行器初始出水倾斜角为45°的情况。图3给出了密度为500 kg/m3的航行器在临界速度和临界推力的作用下,航行器出水成功,并达到临界状态的过程(粗实线为航行器质心运动轨迹)。

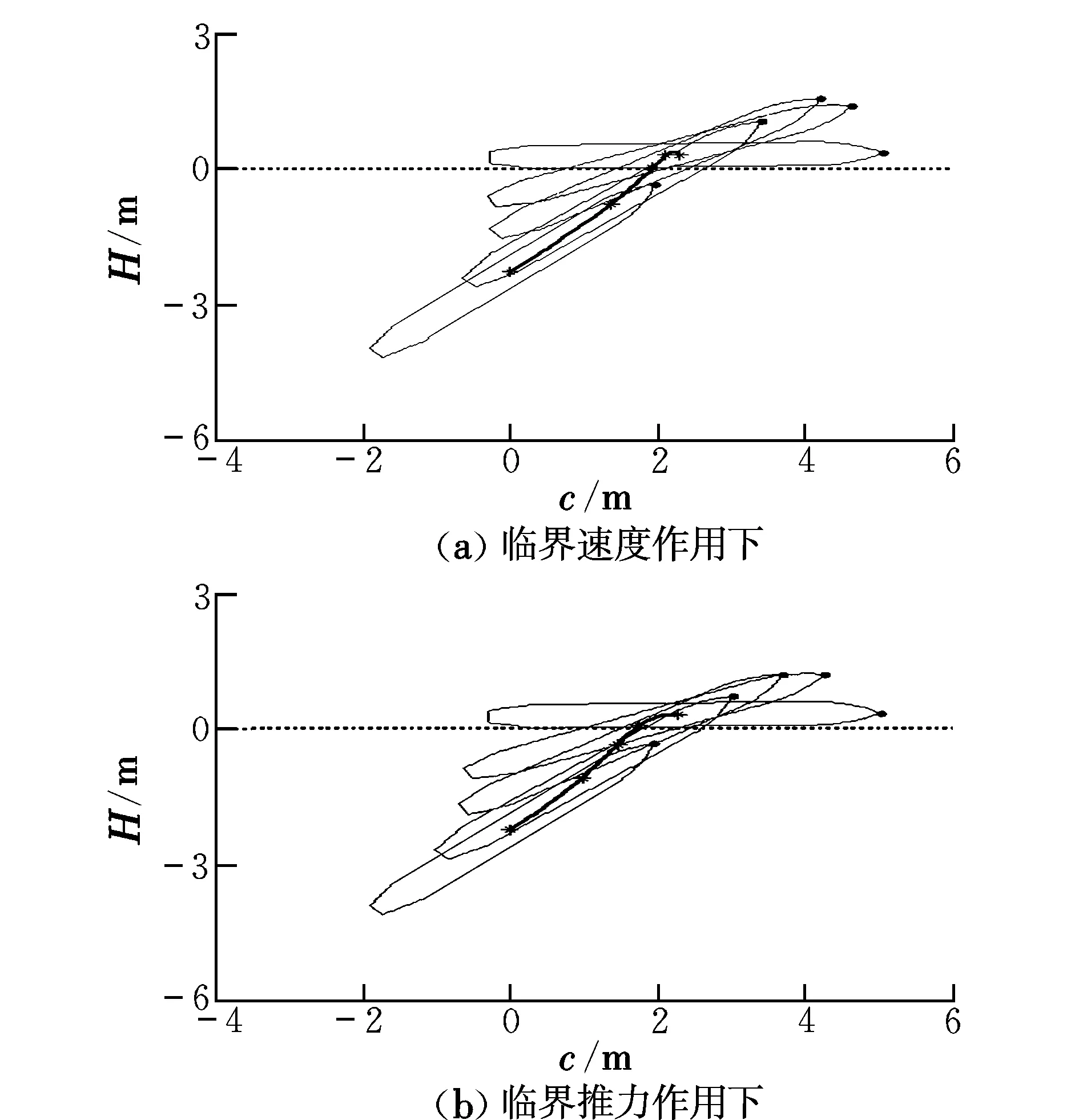
图3 航行器临界出水状态Fig.3 Vehicle’s water-exit process under critical condition

2.2 临界出水状态分析

基于所建立的圆柱体航行器出水模型,在不同的密度条件下,分别对不同密度航行器的临界速度和临界推力进行仿真计算。设定航行器的密度范围从100～1 900 kg/m3,以100 kg/m3为间隔逐渐增加,选择19种不同密度进行仿真计算。

2.2.1 临界速度分析

分别计算初始推力为0 N和初始推力为1 000 N的条件下,航行器能够成功出水的临界速度。计算得到不同密度航行器的临界速度值,以及密度与临界速度的关系曲线，如图4所示。可以看出,航行器能够成功出水的临界速度随着密度的逐渐增加呈一条开口向上的类二次抛物线,必然存在一个最低点。航行器的密度从100 kg/m3增加到900 kg/m3,临界速度逐渐变小,而且变化的程度大致可以分为两个阶段:从100～300 kg/m3,航行器的临界出水速度几乎呈直线下降;从300～900 kg/m3,临界速度的大小呈现缓慢递减的趋势,并且在密度值等于900 kg/m3时,得到最小的航行器出水临界值。从900～1 900 kg/m3,航行器的临界出水速度缓慢增加。由于本次计算变量设定的原因,并不能准确地找出能够得到最小临界出水速度的航行器的密度值;然而通过所得的数据和图形的比较可以发现,该密度值位于900～1 000 kg/m3之间。因此,在一定的初始推力的条件下,这个密度区间的航行器在出水的过程中,成功出水所需的速度最小。

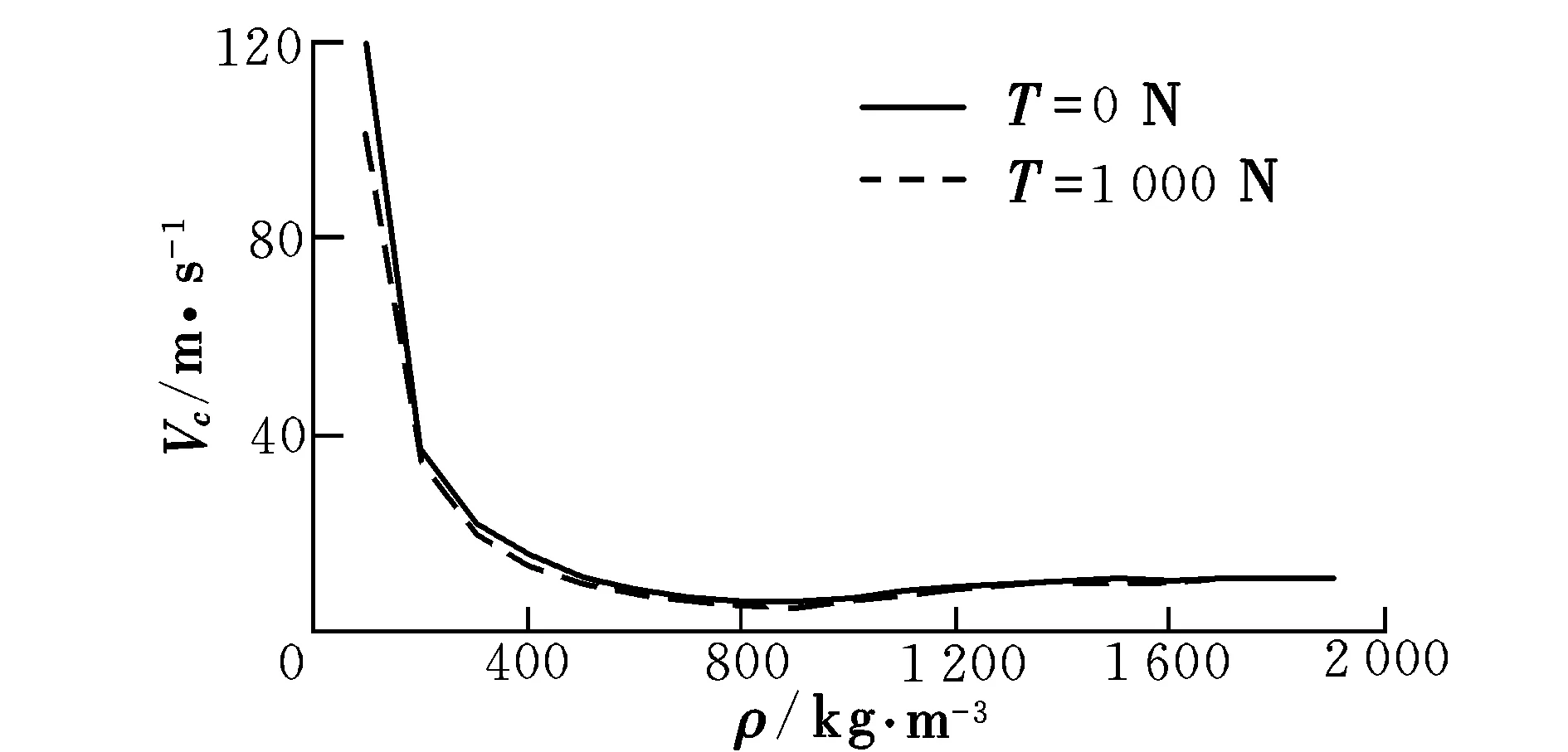
图4 临界速度值Fig.4 The values of critical velocity

由图4还可以发现,除了因为推力为0导致出水临界速度相应地变大了一些之外,临界速度随着密度的变化规律大致相同,并且在900～1 000 kg/m3这个区间内存在能够使航行器出水所需的临界速度最小的密度值。

2.2.2 临界推力分析

分别计算在速度为5 m/s和1 m/s的条件下,刚好能够推动航行器成功出水的临界推力的大小。不同密度航行器的出水临界推力值,以及航行器密度与临界出水推力的关系曲线如图5所示。

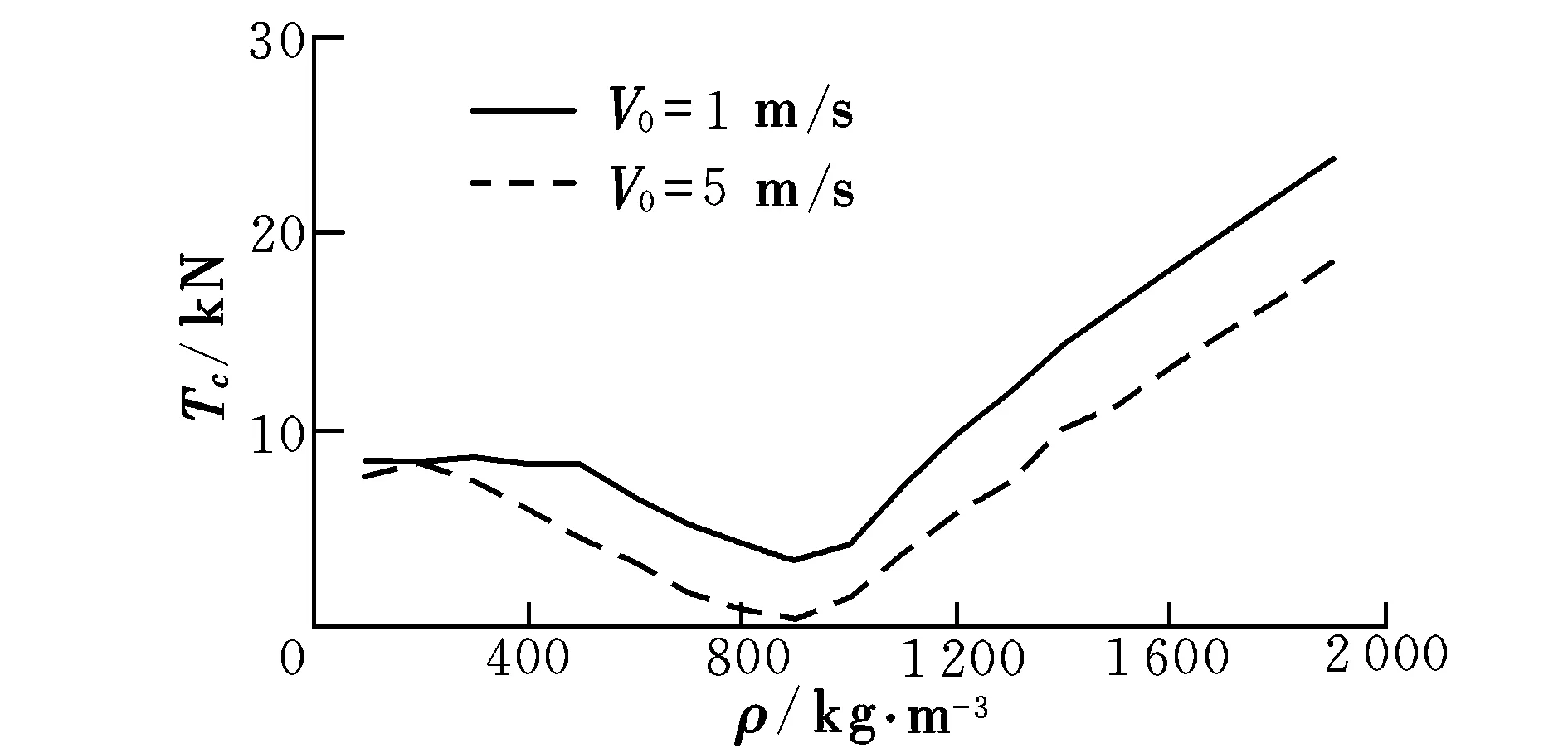
图5 临界推力值Fig.5 The values of critical thrust

由图5可以看出,航行器刚好能够成功出水的临界推力值随着航行器密度的变化呈开口向上的类二次抛物线。除了在密度为200 kg/m3时出现一定的误差外,从100～900 kg/m3,不同密度航行器的临界推力值逐渐减小,当航行器密度为900 kg/m3时,所需要的临界推力值最小;从900～1 900 kg/m3,航行器能够刚好成功出水的临界推力值逐渐增加。类比临界速度的结论,由于计算变量设定的原因,无法得到最小临界出水推力的密度值,但该密度值存在于900～1 000 kg/m3区间内,即密度在该区间内的航行器出水过程所需要的临界推力最小。由于设定的航行器出水初速度减小了,所以可以看到为了弥补出水所需要的动能,航行器的出水临界推力值相应地增大了;但是随着密度的变化,临界推力值的变化规律与速度为5 m/s时的变化规律基本一致,且900～1 000 kg/m3密度区间依然是所需出水临界推力值最小的区间。

3 结论

通过对本文所得到的计算结果进行分析和比较发现,在出水过程中,密度较大和较小的航行器都不是最利于出水的选择,只有密度在一定区间内的航行器,方可以相对较小的速度和推力成功出水。该密度区间即900～1 000 kg/m3。本文结论对后续出水航行器的设计和结构优化均具有一定的指导和参考意义。

[1] Karman V T,Wattendore F L.The impact on seaplane floats during landing[R].NASA-TN-321,1929.

[2] Huang J,Zeng G.Finite-element strength and stability analysis and experimental studies of a submarine-launched missile’s composite dome[J].Engineering Structure,2000,22(9):1189-1194.

[3] 尹翔,冯金富,吝科,等.基于Creator和Vega的水空跨越航行器视景仿真[J].飞行力学,2013,31(5):477-480.

[4] 邹星,李海涛,宗智.基于VOF模型的结构物出水过程数值模拟[J].武汉理工大学学报:信息与管理工程版,2012,34(5):558-561.

[5] 尤天庆,张嘉钟,王聪,等.航行器出水过程头部流场载荷特性分析[J].北京航空航天大学学报,2011,37(5):610-614.

[6] 严卫生.鱼雷航行力学[M].西安:西安工业大学出版社,2005:26-27.

[7] 魏暄荪,刘昌礼,黄长强.导弹/弹丸飞行力学[M].西安:空军工程学院,1996:76-78.

[8] 罗格维诺维奇T B.自由边界流动的水动力学[M].施红辉,译.上海:上海交通大学出版社,2012:127-156.

(编辑：李怡)

The effect of water-air crossing vehicle’s density on water-exit

YU Zong-jin, FENG Jin-fu, XU Bao-wei

(Aeronautics and Astronautics Engineering College, AFEU, Xi’an 710038, China)

In order to simulate the water-exit process of vehicle, and study the effect of vehicle’s density on the process when vehicle is exiting water. Combining with the ideal fluid and viscous fluid effects on aircraft, the dynamics model for cylinder vehicle’s water-exit was established. In the process of vehicle’s water-exit, the variation of physical factors like buoyancy, center of buoyancy etc were considered while. The critical velocity and thrust that make vehicle successful to exit water were calculated respectively under different density. At last, the relationships between vehicle’s density and critical velocity and thrust were obtained respectively.

density; dynamics model; water-exit; critical velocity; critical thrust

2015-01-12;

2015-04-25;

时间:2015-06-24 15:03

余宗金(1990-)，男，四川华蓥人，硕士研究生，研究方向为兵器科学与技术。

V211.8

A

1002-0853(2015)05-0460-04