激光驾束制导导弹抗侧风作用控制方法

赵辉, 赵斌, 卢晓东, 周军

(西北工业大学 精确制导与控制研究所, 陕西 西安 710072)

激光驾束制导导弹抗侧风作用控制方法

赵辉, 赵斌, 卢晓东, 周军

(西北工业大学 精确制导与控制研究所, 陕西 西安 710072)

针对激光驾束制导导弹抗侧风干扰问题,基于减载控制思想,提出了一种通过控制气流侧滑角的大小来实现姿态修正的方案。在不增加弹上设备的前提下,由惯组信息估计得到实时气流侧滑角,进而将其反馈到控制回路,通过调节修正系数来抵抗侧风造成的导弹横向过载。六自由度仿真结果表明,在24 m/s的侧风干扰下,不加侧风修正方案的导弹会脱离激光波束,而改进方法的制导线偏差则快速收敛,脱靶量小于0.1 m,证明了该方法的有效性。

侧风干扰; 气流侧滑角; 侧向偏差; 弹道修正

0 引言

风速是影响弹道散布的重要因素。激光驾束制导导弹以激光波束作为导引,较大的风速将会使导弹的飞行方向发生变化,脱离有限宽度的波束,从而失去精确打击能力[1]。因此,风干扰对驾束制导导弹的影响不容忽视。

目前对飞行器抗风干扰的研究较多,因控制对象的差异,控制方法也不尽相同。文献[2]将侧风视为常值干扰,导弹控制系统通过观测器反馈来补偿风的影响;但其设计过程繁琐,线性观测器也不能很好地估计干扰值。文献[3]针对飞翼无人机着陆侧风干扰问题,提出了副翼和方向舵联合控制以抵消附加侧滑角的方案;但其控制方式基于实时侧滑角信息,而一般战术导弹的侧滑角无法直接测量。文献[4]运用减载控制思想,在姿态控制方程中加入实时计算出的火箭相对气流的迎角、侧滑角,使火箭具有一种向合成气流飞行的趋势,降低了气动载荷;但该方法依靠发动机推力主动减载,对气动舵控制的导弹并不适用。对于激光驾束制导导弹来说,在不增加弹上设备的前提下,控制系统如何对抗侧风干扰成为其设计过程中的关键。

针对以上内容,本文首先在已有的侧风模型的基础上,分析了侧风对弹道参数的影响。然后针对侧风对驾束制导导弹偏航通道影响较大的问题,提出了一种气流侧滑角反馈的弹体姿态修正方案,并依据典型风场数据,调节修正项系数以减弱导弹所受到的横向过载。此外,针对实时气流侧滑角的获取问题,提出了基于惯组信息的卡尔曼滤波方案。最后通过六自由度仿真验证了本方法对抗侧风干扰的有效性和优越性。

1 侧风的作用

1.1 侧风引起的气流侧滑角

导弹在侧风作用下的相对速度如图1所示[5]。

图1 侧风作用下的相对速度Fig.1 Relative speed under the action of crosswind

将风速W由惯性系通过转换矩阵L′(θ,ψ,γ)转到弹体系,再由速度三角形得到空速VK在弹体坐标系的分量为:

(1)

式中:[Vkx1,Vky1,Vkz1]T为空速Vk在弹体坐标系下的分量;θ,ψ,γ分别为俯仰角、偏航角和滚转角。

根据文献[6]气流侧滑角定义可得:

sinβ*=Vkz1/Vk1

(2)

其中:

将式(1)中的空速分量[Vkx1,Vky1,Vkz1]T代入式(2),即可得到气流侧滑角β*。

1.2 对侧风干扰的修正措施

侧风作用在弹体侧滑角平面,相当于对弹体施加了均匀分布的力Fy。一般情况下力的作用点与弹体质心并不重合,产生的气动力矩会使弹体偏斜,产生侧滑。表1中列出了激光驾束制导导弹在不同风速下的偏航角与标准弹道偏航角的差异值。

表1 不同风速下偏航角偏离情况Table 1 Yaw angle deviations at different wind speeds

导弹侧向受力为:

Fy=LsinγV+CcosγV

(3)

式中:L为升力;C为侧向力;γV为速度滚转角。在γV不大的情况下,上式近似表达为:

(4)

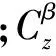
进行弹道修正的目的是使导弹纵轴与空速矢量一致,使导弹具有一种向合成气流方向飞行的趋势。实际情况是尽可能使气流侧滑角减小,以减少作用在弹体上的气动载荷,从而达到卸载的目的[7]。

本文通过将实时计算的气流侧滑角β*引入到控制量u,成为附加控制项,改进后控制量形式为:

u=u0+kββ*

(5)

式中:u0为未加修正时的控制量;kβ为修正系数,其大小表征修正能力。

考虑短周期运动方程[8]:

(6)

式中:Δψ为偏航角;Δδy为控制量;Mgy为干扰力矩。若不考虑侧滑角反馈,控制量可表示为:

(7)

将式(12)代入式(11),得到:

b28Mgy+b24βw

(8)

(9)

要减小气流侧滑角,应设法使Δβ去抵消βw。

(10)

将气流侧滑角反馈到控制项中,得到:

(11)

将式(11)代入式(6),并忽略动态项后得:

(12)

(13)

2 实时侧滑角的估计方法

工程实际中获得实时侧滑角的方法一般有两种:一种是通过弹上传感器直接获得,如飞机上的迎角传感器等;另一种是借助导弹动力学模型,以惯组数据的姿态角和姿态角速度为量测值,利用卡尔曼滤波或其他非线性观测器估计出侧滑角。由于后者克服了对硬件的依赖性,并且只要动力学建模的准确度高,滤波精度也会越高,故本文采用第二种方法。

采用线性化后的动力学模型,其状态方程和观测方程如下[9]:

(14)

z(t)=[0 0 1 1][αβωyωz]T+v(t)

(15)

式中;α为迎角;ωx为滚转角速度,为耦合项,由惯组信息给出;w(t)为系统噪声矩阵;v(t)为观测噪声矩阵。选取状态变量X=[αβωyωz]T,输入量u=[δyδz]T,令

状态方程可简写为:

(16)

观测方程为:

z(t)=Hx(t)+v(t)

(17)

选取离散时间常数T=0.01 s,对状态方程和观测方程离散化,采用标准卡尔曼滤波过程进行滤波,得到最优的侧滑角估计值[10]。

选取系统噪声方差矩阵Q(k)时应保证其为对称的半正定矩阵,观测噪声矩阵R(k)为正定的对称矩阵。滤波流程如图2所示。

图2 滤波流程图Fig.2 Flow chart of filtering

3 仿真结果及分析

图3 估计值与真值对比Fig.3 Comparison of estimated values and true values

图4 修正前后气流侧滑角对比Fig.4 Comparison of air flow sideslip angles before and after correction

图5 修正前后侧向偏差对比Fig.5 Comparison of lateral deviations before and after correction

由图3～图5可以看出,卡尔曼滤波值与真实值相差不超过0.3°,可以满足一定的精度要求。采取修正措施后,气流侧滑角β*在幅值上减小,即作用在弹体上的横向过载减小;侧向偏差峰值Zlmax下降到3 m以内,保证了导弹在10级侧风的影响下不脱离激光波束。图6为启控3 s后引入风干扰的侧向偏差对比情况,图7为对应的弹道曲线。

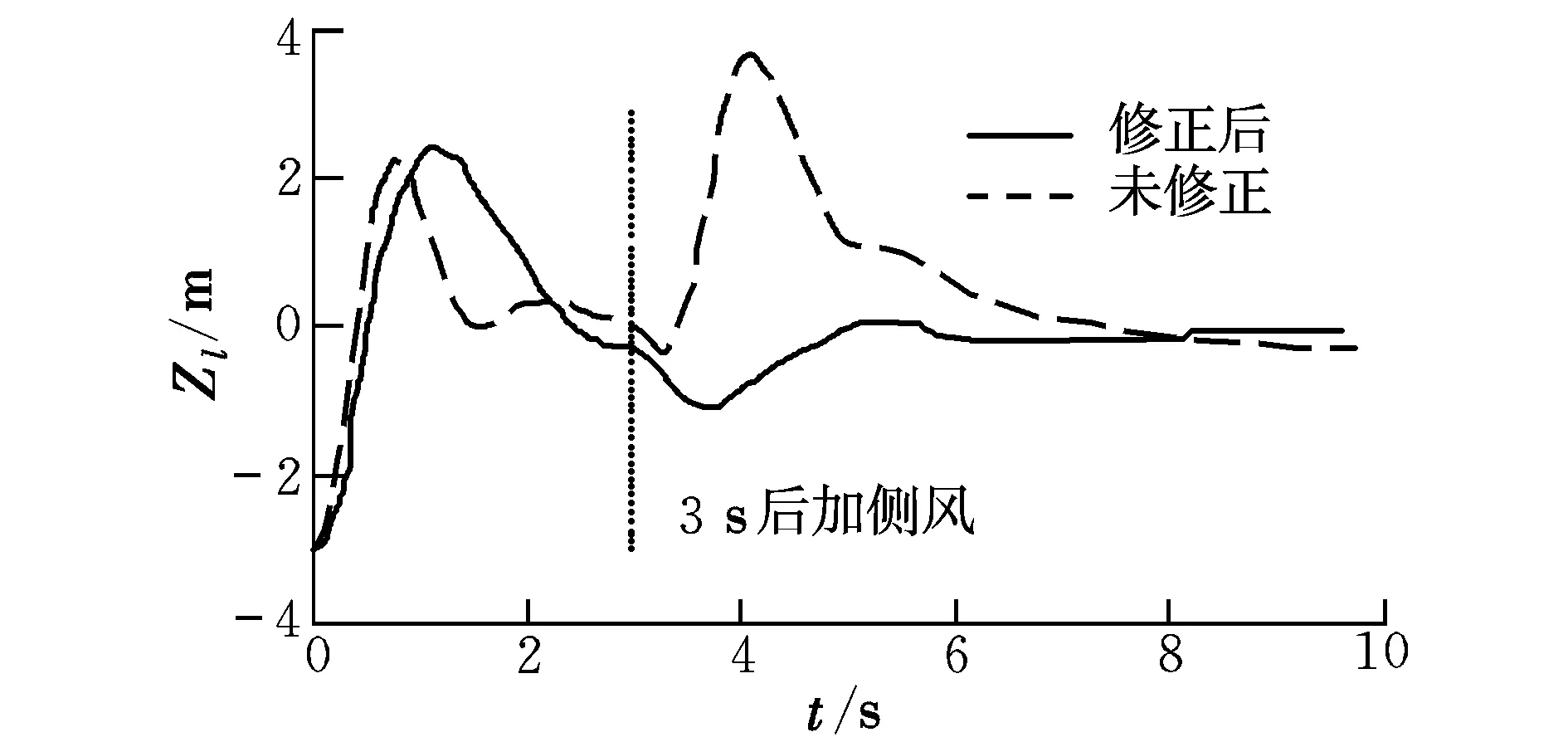
图6 引入侧风后侧向偏差对比Fig.6 Comparison of lateral deviations with crosswind

图7 弹道曲线Fig.7 Trajectory curve

由图6和图7可以看出,未修正控制方法的侧向偏差超调量大,幅值也超出了激光半径;而修正后的曲线平滑收敛,抗风性良好。

表2列出了不同风速下修正前后侧向偏差峰值Zlmax、稳态时间tess(侧向偏差幅值低于Zmax×5%的时刻)以及脱靶量T的具体数据(其中“∞”表示侧向偏差并未收敛到Zmax×5%区域)。

表2 修正前后参数比较Table 2 Comparison of parameters before and after correction

由表2可以看出,修正前Zlmax均超过了3 m,即飞离激光波束,而修正后既保证了导弹始终在激光波束内飞行,又保证了高精度打击能力,脱靶量T小于0.1 m。采取修正措施后线偏差的稳态时间延长了,这是时变的侧滑角信息作为附加控制项持续作用的结果,但是在整个收敛过程中波动的幅值是在容许范围内的。

4 结束语

本文主要研究了激光驾束制导导弹抗侧风干扰问题,通过将实时气流侧滑角反馈到控制端,达到了弹道修正的目的,并保证了高打击精度、简化了弹上设备。本文方法形式简单,容易实现。在今后的研究中,将加入复杂的风模型,综合考虑大气运动对弹道的影响;通过预先仿真,得到修正系数表,根据风速和风向进行插值获得修正系数。另外为了提高导弹在风干扰下的命中率,也可以通过训练射手、修正初始发射角[11]来减弱风的影响。

[1] 王婷,周军.驾束制导导弹一体化制导控制系统设计[J].西北工业大学学报,2009,27(2):173-176.

[2] 杨绍卿.反坦克导弹控制系统设计的状态空间法初探——风及未知常值干扰的补偿问题[J].兵工学报:弹箭分册,1985(1):21-29.

[3] 王艳丽,周洲,张琳.飞翼无人机侧风着陆控制方法研究[J].飞行力学,2009,27(1):24-26.

[4] 李效明,许北辰,陈存芸.一种运载火箭减载控制工程方法[J].上海航天,2004 (6):7-9.

[5] 李卫丽,严洪森,张维琴.风干扰下某型导弹的弹道仿真 [J].计算机技术与发展,2011,21(1):246-249.

[6] 李新国,方群.有翼导弹飞行动力学[M].西安:西北工业大学出版社,2004:5.

[7] Mori H.Control system design of flexible-body launch vehicles [J].Control Engineering Practice,1999,7(9):1163-1175.

[8] 郭广明,罗琴.侧向运动耦合对导弹稳定裕度的影响[J].飞行力学,2013,31(3):250-254.

[9] 黄汉桥,黄长强,赵辉.考虑前馈作用的BTT导弹自动驾驶仪设计方法研究[J].西北工业大学学报,2012,30(3):307-313.

[10] 周凤岐,卢晓东.最优估计理论[M].北京:高等教育出版社,2009.

[11] 孙百安,姜水平.风对BL-1A型增雨防雹火箭弹道的影响及修正 [J].气象科技,2010,38(5):625-628.

(编辑：李怡)

Crosswind-proof control technique for laser beam-rider guidance missile

ZHAO Hui, ZHAO Bin, LU Xiao-dong, ZHOU Jun

(Institute of Precision Guidance and Control, NWPU, Xi’an 710072, China)

For the crosswind disturbance of the laser beam-rider guidance missile, an attitude correction program was proposed by controlling the air-path angle of sideslip based on the load control theory. In the premise of not increasing the equipment on the missile, the real-time air-path angle of sideslip was obtained by the estimated inertia unit information, and then was fed back to the control terminal. The lateral overload was decreased by adjusting the correction coefficient. The 6-DOF simulation results show that the missile without crosswind correction program is driven away from the laser field, while the guidance range errors of the improved method is fast convergence, the miss distance is less than 0.1 m under a crosswind disturbance at a speed of 24 m/s. It indicates that the modified method is effective.

crosswind disturbance; air-path angle of sideslip; lateral deviation; trajectory correction

2015-12-15;

2015-04-22;

时间:2015-06-24 15:03

西北工业大学基础研究基金资助(JCT20130101)

赵辉(1990-)，男，河北衡水人，硕士研究生，主要从事飞行器制导与控制技术研究。

TJ765

A

1002-0853(2015)05-0435-04