高持续荷载下的混凝土徐变破坏试验

谢 竞 吴韶斌

（湖南水利水电职业技术学院 长沙市 410131）

处于复杂环境中的水工混凝土结构在服役期间承受自重、水压力和温度应力等持续荷载，其作用时间长达数十年。众多理论与试验研究表明这类混凝土在其设计寿命周期内强度产生劣化甚至破坏。忽视这种长期持续荷载下的强度劣化影响，对混凝土结构的设计，安全耐久性评价是不利的。受试验设备和试验难度的制约,对混凝土在高持续作用下产生徐变破坏的试验成果还不能很好地解释其破坏机理。

研究荷载水平与持荷时间对混凝土长期强度的影响可以为评价混凝土抗裂设计、提高其设计寿命提供依据,为混凝土结构的安全性、耐久性提供参考。

1 混凝土徐变破坏试验研究

1.1 原材料与配合比

试验采用重庆金井源建材厂生产的32.5级的普通硅酸盐水泥，中砂、（5～20）m粒径的碎石，混凝土的配合比0.48∶1∶1.47∶2.74（水∶水泥∶河沙∶碎石）。

1.2 试件与加荷装置

弯曲受拉试件采用尺寸为100mm×100mm× 100mm试件，目前徐变试验的加荷载主要有弹簧式液压仪、杠杆式拉伸徐变仪等，但都并不能很好地适用混凝土试件弯曲下的徐变变形测量。本文自行设计了一个简单、较可靠的加载装置。如图1所示。

图1 徐变试验加载装置及控制系统

1.3 持荷水平

混凝土在较低的持续应力水平以下需要持荷数月甚至数年才发生破坏，而目前加荷的液压试验机不能进行长时间的持荷，本次徐变破坏采用应力强度因子（σc/fc）0.8以上的持荷水平，σc为持荷应力，fc为短期荷载下的混凝土强度，应力水平σc/fc分别为0.8，0.0.85，0.90，0.95进行试验。

1.4 试验设计

在通过短期强度试验得到本次试验混凝土试件的抗压强度fc后，采用RMT-150C岩石力学试验试验机，最大荷载为1000kN。RMT-150C试验系统，分别对4组试件进行混凝土分别在 80%，85%，90%，95%强度下的持续荷载抗压试验。在荷载达各应力水平后维持稳定不变，观察混凝土在持续荷载下的破坏形式和记录破坏时间；如若试件经历2h的持续相应荷载仍未破坏，再以1kN/s的恒力控制加载直至试件破坏，记录破坏时间与经过持荷后破坏的极限强度。

2 抗压徐变破坏试验结果及分析

2.1 破坏时间

本试验的结果表明，在持续荷载作用下，试件的徐变破坏时间普遍存在明显的离散性，为此，采用每组试件的平均破坏时间作为试验结果。如附表。

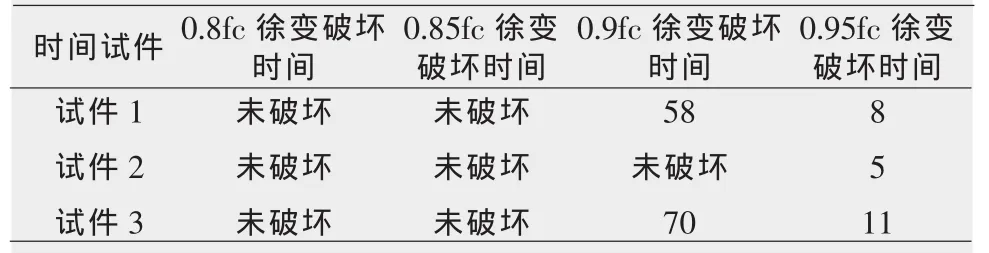
附表 各持荷水平下徐变破坏时间 min

从附表可以看出高持续荷载下的混凝土在低于其抗压强度时就会发生破坏。在95%单轴抗压强度的荷载下混凝土在大约经过6min左右就发生破坏。而在90%抗压强度下混凝土的破坏时间在64 min左右。由于本文单轴抗压徐变试验中的加载采用液压机，不能进行长时间的加载，只设计了为期2 h的持荷时间。试验还观察到，在2h相应的恒定的荷载下如果试件未发生破坏，以1kN/s的恒力控制加载后，试件破坏的时间低于短期强度试件组的破坏时间，破坏的极限强度也低于混凝土的抗压强度。应力强度因子越大，破坏时间越短，强度也越低。这表明在持荷过程中混凝土的变形在增加，损伤在发展，导致在低于其短期抗压强度试件就发生破坏。

2.2 受压徐变变形

采用RMT-150C岩石力学试验机控制系统得到以位移表示的变形与持荷时间的关系，如图2。

从图2看出混凝土的徐变变形大致分为三个阶段，在前期变形增长较快，随着时间的增加变形的增长速率放慢。经过较长时段的持荷后，变形开始急剧增加。增长速率也成不收敛性。混凝土徐变变形在高持续荷载下表现为非线性。同时通过比较90%荷载水平以上与以下的徐变变形曲线，可以认为上文的徐变破坏在低于90%荷载水平的破坏发展趋势是合理的。即在80%、85%荷载水平下的混凝土也会发生徐变破坏。其荷载越高，破坏时间越短。

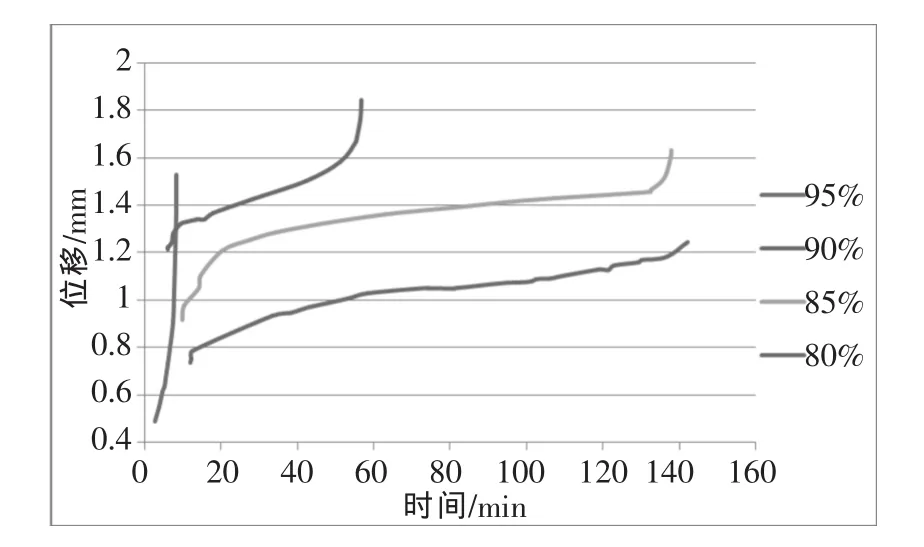
图2 不同持续荷载下的抗压徐变变形曲线

众多试验与理论均表明，高持续荷载的混凝土徐变历经三个阶段（图3）：稳定的徐变阶段、徐变减速阶段、徐变加速阶段。在徐变加速阶段，高应力下混凝土的微裂缝不断地扩展，微裂纹发生失稳扩展导致混凝土内部产生损伤，形成宏观的裂缝，这一阶段的徐变变形随时间增加继续增加，且徐变的增加速率迅速变大，不再收敛，混凝土结构也发生破坏。此时混凝土徐变变形表现为非线性。

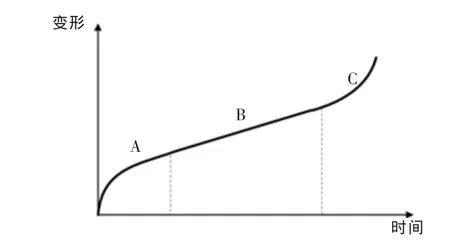
图3 较高荷载下混凝土的徐变破坏

根据徐变变形的三个阶段，可将混凝土在高持续荷载下的应变表示为：

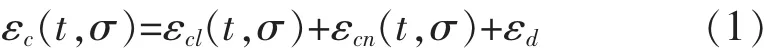
式中 εcl（t，σ）——加载初期可恢复的迟后弹性变形和由荷载作用下混凝土凝胶空隙中水的流动产生的不可恢复流动变形，为线性徐变；

εcn（t，σ）——混凝土徐变减速阶段非线性徐变，它主要与微裂纹的扩展有关。

εd——混凝土第三阶段的变形，它主要为损伤变形。

根据鲍尔次曼(LBolztmna)迭加原理，线性徐变εcl（t，σ）可以采用以下公式计算。

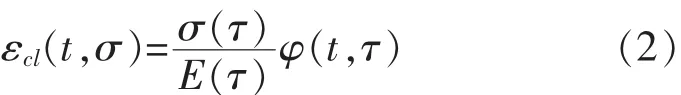
式中 φ（t，τ）——徐变系数。

σ（τ）——t时刻作用于混凝土单轴常应力。

E（τ）——弹性模量。

目前亦认为叠加原理也适用于非线性徐变的计算，通过一些改进与调整（如随龄期调整有效模量法）将非线性问题转为线性问题来计算混凝土的非线性徐变。

混凝土的徐变破坏过程是大量微裂纹产生、扩展和相互作用，直至形成宏观裂纹并发生失稳扩展导致的。当混凝土承受荷载时，材料内会累积应变能；荷载越高，应变能越大。当应变能超过一定限度后，导致混凝土的损伤破坏。损伤变量D定义为材料中发生破坏的微单元数量 NF与总单元N的比值，根据Lemaitre的损伤力学理论，混凝土等脆性材料的本构关系可以表示为：

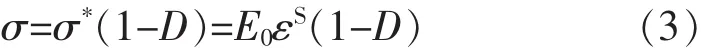
可假设混凝土单元强度P服从 Weibull分布，可将（3）中的D表示为：

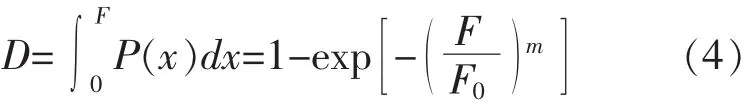
式中F为材料微单元强度。

根据（4）可以得到单轴持续荷载下混凝土的应力应变关系：

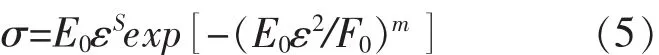
3 结论与展望

混凝土在持续高荷载下会发生徐变破坏，荷载越高，破坏时间越短，破坏时间具有离散性；在较高的持续荷载下混凝土的徐变具有依时性，应力水平超过0.80fc，徐变急剧增加。即使荷载不增加，变形仍然继续增加，荷载水平越高，变形增加得越快越高。经过一段稳定荷载的持续时间后混凝土破坏，徐变变形表现为非线性。

由于只进行了强度因子在0.8以上的混凝土受压徐变试验，对于在多大荷载水平下混凝土将发生破坏，其变形呈非线性，文中试验并不能确定，而这是工程设计中关心的问题。高持续荷载下混凝土徐变破坏试验仅对初步混凝土徐变变形及破坏进行试验研究，今后还需要进一步的试验与理论研究，分析高持续荷载下混凝土破坏的机理。

[1]欧进萍.重大工程结构的累积损伤与安全度评定[R].走向21世纪的中国力学——中国科协第9次 “青年科学家论坛”报告文集,北京:清华大学出版社,1996.

[2]惠容炎，黄国兴，易若冰.混凝土的徐变[M]:中国铁道出版社，1988.

[3]熊维.不同强度早龄期混凝土徐变及徐变对长期荷载作用下预应力构件的影响[D].天津:天津大学，2011.

[4]尹志府，混凝土强度等级与徐变的关系[J].混凝土，1991，（6）:21-23.

[5]王德法,张浩博,黄松梅.混凝土受拉徐变中破坏时间与持荷应力关系研究[J].西安交通大学学报.1999，33（10）:104-105.

[6]张子明,周红军,殷波,基于等效时间的混凝土徐变[J]河海大学学报，2005，（3）:173-17.

[7]李兴贵.高拉应力作用下混凝土的徐变和徐变破坏[J].河海大学学报.1996，24（4）.

[8]李兴贵，周耀文.混凝土在不同介质中持续高拉应力下的徐变破坏试验研究[J].水利水电技术，1996，（3）:58-62.