基于ANSYS的摆线齿锥齿轮有限元模态分析与研究

张志民，樊喜刚，周志刚，高善柱，鞠伟华

(北京星航机电装备有限公司 技术中心，北京 100124)

基于ANSYS的摆线齿锥齿轮有限元模态分析与研究

张志民，樊喜刚，周志刚，高善柱，鞠伟华

(北京星航机电装备有限公司 技术中心，北京 100124)

摘要：研究了摆线齿锥齿轮的固有振动特性，考虑到摆线齿锥齿轮的特点，利用三维软件Pro/E进行了精确参数化建模，以有限元方法理论为基础，通过有限元分析软件ANSYS对齿轮进行模态分析，得到了10阶固有振动频率、模态振型和应力、应变云图，为齿轮系统的振动特性分析、振动故障诊断和预报以及结构动力特性的优化设计提供了依据，为摆线齿锥齿轮系统的动态设计和减少振动等方面提供了理论依据；同时，为齿轮系统的动态响应计算和分析奠定了基础。

关键词：摆线齿锥齿轮；模态分析；有限元法；固有频率

摆线齿锥齿轮是机械传动中最重要的部件，为了保证齿轮传动过程的平稳可靠，减小振动和噪声，应对齿轮传动系统固有特性进行分析。模态是齿轮的固有振动特性，每一阶模态具有特定的固有频率、阻尼比和模态振型，齿轮系统的模态特性可为齿轮系统的振动特性分析、振动故障诊断和预报以及结构动力特性的优化设计提供依据。在齿轮设计初始阶段很难得到其固有振动特性的试验数据，只能通过理论计算得到其动力学分析的相关参数，目前，大多数人使用有限元分析法。本文利用三维软件Pro/E对摆线齿锥齿轮进行精确的参数化建模，并在有限元分析软件ANSYS中对其进行模态分析，得到了各阶固有振动频率、振型和应力、应变云图，并对其进行了研究，针对摆线齿锥齿轮系统设计提出了几点建议，为减少振动和噪声等方面提供了理论依据，为齿轮系统动态响应分析奠定了基础。

1模态分析理论依据

由弹性力学有限元理论可得到齿轮传动系统的运动微分方程：

(1)

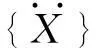
若无外力干扰，即{F(t)}={0}时，可将齿轮系统视为自由振动，得到齿轮系统的自由振动方程。在求齿轮系统的振动特性(固有频率和固有振型)时，系统的阻尼对其影响不大，因此可以忽略阻尼项，得到1个关于无阻尼自由振动的运动微分方程：

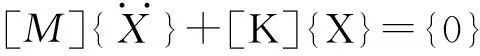
(2)

设X=Usin(wit+φ)，则有：

(3)

令式3的系数行列式等于零，即可求得第i阶模态固有频率wi，i=1,2，…，n，向量ui为其对应的主振型。这时求出的系统固有频率有n个,同时对应着n个模态振型，固有频率wi和模态振型向量ui构成了系统的第i阶自然模态，它表征了一种系统的同步运动。显然，一般n自由度系统有n种同步运动，每种运动均为简谐运动，但频率wi不同而且其振幅在各自由度上的分配方式即模态向量ui也不相同。

模态分析的最终目的在于识别出系统的模态参数，为结构系统的振动特性分析、振动故障诊断和预报以及结构动力特性的优化设计提供依据。在有限元分析软件ANSYS中，模态分析是一个线性分析过程，该软件提供了多种分析方法，最常用的分析方法为Subspace法。本文完成的模态分析主要包括建立参数化模型、导入ANSYS加载、求解、扩展模态和查看结果。

2建立齿轮参数化模型

三维软件Pro/E可以很好地与ANSYS有限元分析软件结合，并且在Pro/E软件中建模相对更快捷、方便。在Pro/E软件中，根据表1中的数据对摆线齿锥齿轮进行参数化建模，根据参考文献[1-2]对摆线齿锥齿轮进行参数化建模，摆线齿锥齿轮的参数化模型如图1所示。

表1　摆线齿锥齿轮参数

图1　摆线齿锥齿轮参数化模型

3摆线齿锥齿轮的模态分析

3.1导入、加载并求解

图2　有限元模型

在Pro/E中软件建立好摆线齿锥齿轮参数化模型后，点击菜单工具栏中“ANSYSGeom”按钮，将齿轮模型导入ANSYS软件的经典模式中，对齿轮零件做模态分析。本文中摆线齿锥齿轮采用40Cr合金钢材料，因此在材料属性中定义弹性模量E=2.1×105MPa、泊松比μ=0.3、密度ρ=7.8×10-6kg/mm3。选用单元类型Solid Brick 20node 186,该单元类型是一个高阶三维固体结构单元，适用于CAD/CAM中不规则的复杂模型，该单元有20个节点，每个节点有3个沿着xyz方向平移的自由度，具有任意的空间各向异性，单元支持塑性、超弹性、蠕变、应力刚化、大变形和大应变能力。采用自由划分网格方法得到合适的有限元模型，如图2所示[3-7]。

求解过程中，选择分析类型为model，在模态提取方法中选择“block lanczos”并在提取模态数和模态扩展数文本框中输入10，这样在求解中可获得10阶的模态的固有频率，同时选择“Calculate elem result”复选框。求解前需对摆线齿锥齿轮进行合理的自由度约束，本文选择齿轮孔的内表面为约束面，设置约束其所有的自由度，即在对话框中选择 “ALL DOF”，数值设置为0，最后单击“Solve LS”可获得摆线齿锥齿轮的10阶模态的固有频率，见表2。

表2　各阶模态的固有频率

弯曲振主要表现为轮齿的弯曲振动；伞型振为轴向的振动收缩成伞形振型；对折振主要表现为轴向出现规则波浪振型，在端面上为规则多边形振型，综合起来为结构扭曲型的对折振；圆周振为轴向基本无振动，在端面上为圆周方向的振动；径向振主要表现为齿轮沿径向伸缩，端面出现多边形振型，轴向基本无振动。

3.2结果后处理

本文在求解前已经设置了模态扩展，因此在求得每一阶模态固有频率的同时，ANSYS软件也求解了其对应的主振型(体现在对应固有频率时的齿轮各节点的位移情况)。通过ANSYS分析软件的通用后处理器可以方便地对其进行观察和分析，也可以对各阶主振型进行动画演示，这时就可以在通用后处理模块“Plot Results”中查看各阶固有频率时各个方向上的应力云图和应变云图，如图3所示。

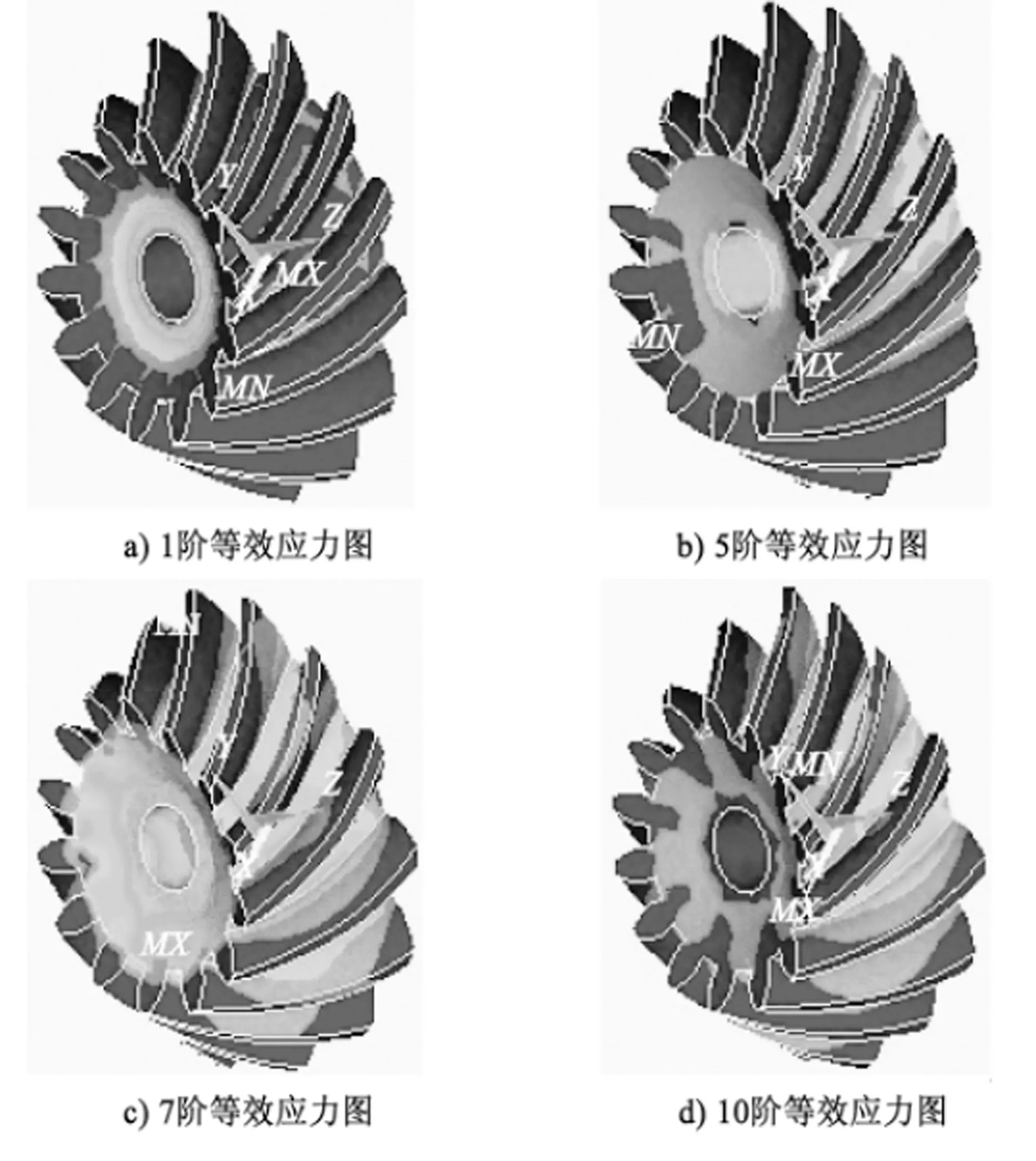
图3　各阶模态的等效应力图

4分析结果研究

从表2可以看出固有频率<50 Hz，从各阶振型动画演示可见各阶位移都呈现齿根较小，齿顶处最大的现象。具体到各阶，由于振型不同，位移云图也随之不同，如1阶固有频率下的振幅各个齿的变化基本相同，其他阶数模态的轮齿的相对振幅各不相同，一些齿振幅较大，其他齿振幅相对较小。从图3可以看出，各阶都呈现出齿根过渡曲线上等效应力值较大，齿顶较小的规律。1～10阶模态时，轮齿中在齿根过渡处的应力值最大，齿顶最小，并且随着阶数增大，应力值变大。

该齿轮适用于高频啮合，在应用时尽量避免其固有频率，这样可以减少齿轮传动时所产生的振动和噪声；在设计齿轮传动系统时，应根据啮合频率对齿轮相应部位进行强度校核和分析。

5结语

通过三维软件Pro/E对摆线齿锥齿轮进行了精确参数化建模,并导入ANSYS软件对其进行模态分析，得到了10阶模态的固有频率和对应的主振型及应力、应变云图。研究了各阶模态振型的特点和应力、应变云图的变化规律，并根据这些特点和规律对摆线齿锥齿轮系统的动态设计和减少振动等方面提供了建议。

参考文献

[1] 汤兆平，孙剑萍.克林贝格摆线齿锥齿轮的精确参数化设计[J]. 机床与液压，2010,38(3):113-116.

[2] 刘明.克林贝格摆线齿准双曲面齿轮建模与仿真[J]. 现代制造工程，2010(9)：57-61.

[3] 孙伏.基于ANSYS的少齿数齿轮模态分析与研究[J].机械设计与制造，2011(5)：119-121.

[4] 汤宏.基于ANSYS有限元软件的斜齿轮振动模态分析[J].中国科技信息，2009 (23)：140-141.

[5] 何亚银.基于有限元法的渐开线直齿圆柱齿轮模态分析[J].装备制造技术，2010 (7)：43-44.

[6] 叶友东，周哲波.基于ANSYS 直齿圆柱齿轮有限元模态分析[J].机械传动，2006,30(5)：63-65.

[7] 陶泽光，李润方，林腾蛟.齿轮系统有限元模态分析[J].机械设计与研究，2000(3)：45-46.

责任编辑李思文

Analysis and Research on Finite Element Modal of Cycloid Bevel Gear based on ANSYS Software

ZHANG Zhimin, FAN Xigang, ZHOU Zhigang, GAO Shanzhu, JU Weihua

(Technology Center, Beijing Xinghang Electrical Equipment Co., Ltd, Beijing 100124, China)

Abstract:The paper studied the natural vibration characteristics of cycloid bevel gear. Based on the theory of finite element method, the order natural vibration frequency, modal vibration mode and stress and strain contours were carried out through the finite element analysis software ANSYS for gear modal analysis, by considering the characteristics of the cycloid bevel gear and using 3D software Pro/E to accurately parameterized modeling. The vibration characteristic analysis of gear system, the vibration fault diagnosis and forecast and optimized the design of dynamic characteristics of the structure was provided theoretical basis. The cycloid bevel gear system dynamic design, reducing vibration, etc was provided the theory basis, as well as the dynamic response of the gear system calculation and analysis was provided a foundation.

Key words:cycloidal tooth bevel gear, modal analysis, FEM, natural frequency

收稿日期：2014-05-12

作者简介：张志民(1986-)，男，助理工程师，主要从事机械制造及自动化和电气化设计等方面的研究。

中图分类号：TH 132.4

文献标志码：A