GM(1,1)模型在某型飞机维修保障费用预测中的应用
2015-03-15孙海霞魏华凯
孙海霞,魏华凯,韩 莉
(海军航空工程学院 青岛校区,山东 青岛 266041)
GM(1,1)模型在某型飞机维修保障费用预测中的应用
孙海霞,魏华凯,韩莉
(海军航空工程学院 青岛校区,山东 青岛 266041)
摘要:基于某型飞机维修费用的历史数据,运用灰色系统理论建立了GM(1,1)模型,对该装备维修保障费用进行了预测, 并对模型精确度进行了验证。结果表明,所建立的模型准确、有效,可以用来对未来几年的维修保障费用进行预测。
关键词:维修保障费用;灰色GM(1,1)模型;预测
随着航空技术的发展,军用飞机技术含量的增加,其维修需求也在迅速增大;因此,无论哪个国家,军用飞机的使用保障需求都是装备决策机构考虑的重要因素。飞机的维修费用(maintenance cost,简称MC)是飞机在规定条件下进行维修, 消耗维修资源(人力和物资)而支付的费用,在飞机整个寿命周期费用中占有较大的比例[1]。为谋求最大的军事经济效益,应对装备所需的维修保障费用进行科学和合理的预测。影响飞机维修费用的因素比较多,可参考的历史数据比较少,对飞机维修费用的预测造成了一定的难度。一般的预测方法,比如参数法和统计回归等都难以进行精确的分析预测。灰色系统理论可以在较少数据等不确定背景下研究数据的处理、现象的分析、模型的建立、发展趋势的预测和事务的决策等工作。针对这种情况,本文采用所需样本数据相对较少的灰色理论预测方法来建立GM(1,1)模型,对我军某型飞机未来几年的维修费用进行预测,这对于得出该型机维修保障需求规律具有直接的应用价值,在考虑机型之间的差距后,其研究方法、思路和所建立的模型可推广应用于其他型号飞机的计划与保障决策。
1灰色GM(1,1)预测模型
灰色系统建模是在削弱原始信息随机性,建立灰色模块的基础上,应用微分拟合法直接将时间序列转化为微分方程,建立的是抽象系统发展变化的动态模型。运用这种模型对系统进行分析,可以反映出系统内部机制变化过程的本质,可用于预测控制。这是一种用不足信息建立信息尽可能充分的模型的途径,是充分发挥白色信息作用的途径,是用离散数据建立微分方程的一种方法,可以使抽象系统模型化和实体化。
GM(1,1)模型的实质是对原始数据做一次累加生成,得1-AGO序列,使生成的数据序列呈一定的规律性,再作一次累减生成,还原求出模拟值,并进行预测[2]。
1.1模型的建立
构建步骤如下。
1)输入原始数列X(0)(非负序列),即X(0)=(x(0)(1),x(0)(2),…,x(0)(n))。
2)对X(0)进行一次累加生成,得1-AGO序列X(1),即X(1)=(x(1)(1),x(1)(2),…x(1)(n))。
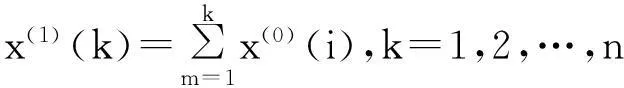
3)Z(1)为X(1)的紧邻均值生成序列,即Z(1)=(z(1)(2),z(1)(3),…,z(1)(n))。
式中,z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1),k=2,3,…,n。
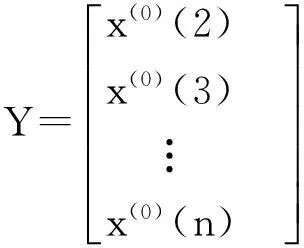
5)得到灰色微分方程为z(0)(k)+az(1)(k)=b。
8)做一次累减生成,得到还原值为:
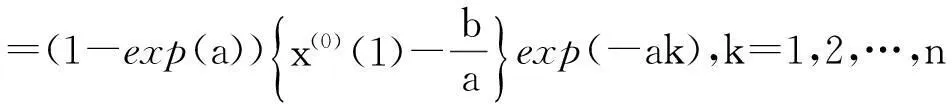
9)检验误差。
1.2模型精度检验及预测值精度评估方法
为确保GM(1,1)模型的预测精度,还需要进行模型精度检验,模型精度检验常用的方法有残差检验、关联度检验和后验差检验等方法[3-6]。本文选用残差检验和后验差检验方法进行检验,方法步骤如下。
1.2.1残差检验
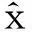
1.2.2后验差检验

按C和p的大小来区分预测精度等级,其中,C和p应同时满足条件。
1.2.3预测值精度评估方法
上述2种检验方法中,相对误差和均方差比值越小越好,小误差概率越大越好。常用的精度等级评估见表1。
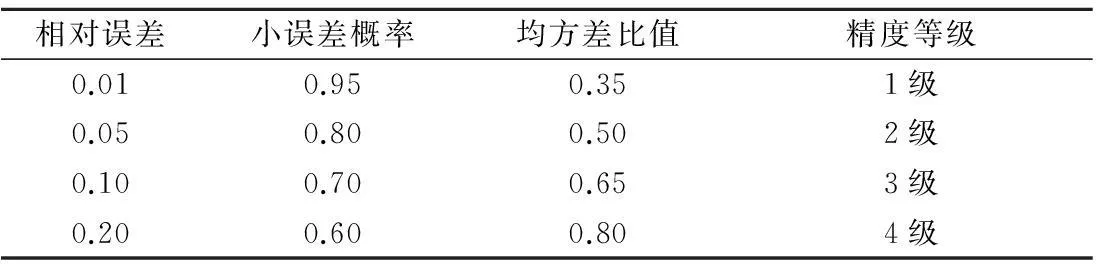
表1 GM(1,1)模型精度检验等级参照表
2基于GM(1,1)模型的某型飞机维修保障费用预测
2.1GM(1,1)模型的建立
某型飞机2008~2013年的年维修保障费用数据见表2。

表2 某型飞机2008~2013年的维修保障费用
将上述数据输入灰色系统理论建模软件中,计算过程和结果如下。
---------Start----------
第1步,原始序列的初始化
初始化后的序列:263,286,291,309,328,345
第2步,原始序列的1-AGO
1-AGO序列:263.00,549.00,840.00,1 149.00,1 477.00,1 822.00,
第3步,1-AGO的紧邻均值生成
紧邻均值生成序列:406.00,694.50,994.50,1 313.00,1 649.50
第4步,发展系数和灰色作用量的计算
a=-0.05b=261.16
第5步,模拟值的计算
263.00,281.31,295.75,310.94,326.90,343.68,
第6步,计算残差
残差=51.28
-----------End----------
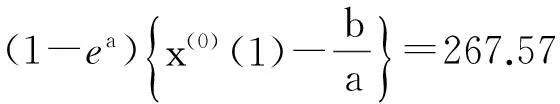
2.2模型精度检验
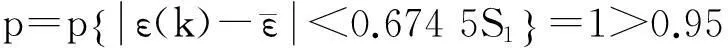
对照表1可知,本模型的预测模拟精度等级为1级,满足精度要求。预测值与实际值的对比情况见表3,通过对比可以看出预测值与实际值相差很小,这也说明模型的精度较高,能较好地预测未来几年发生故障的数量。
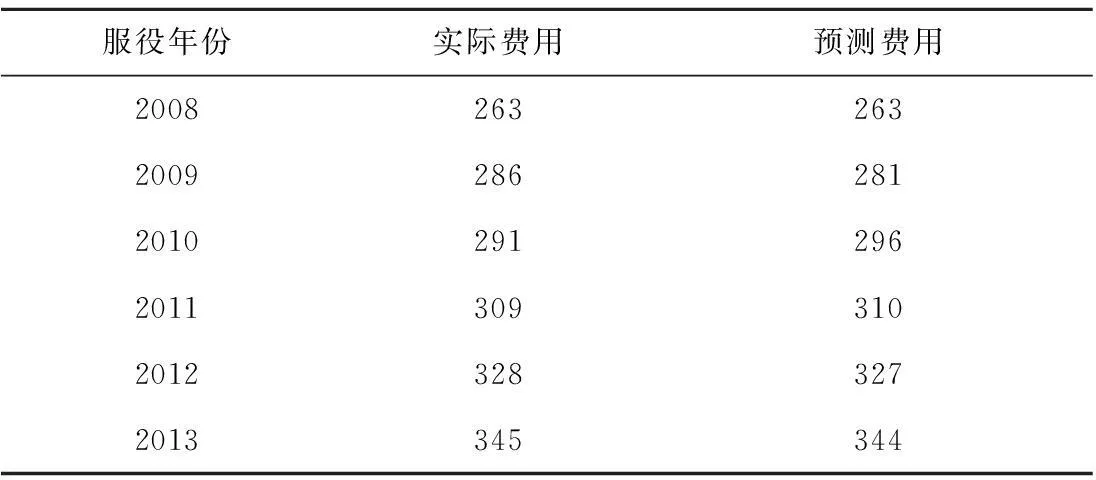
表3 某型飞机2008~2013年的年维修保障费用
3结语
根据某型飞机已有的维修保障费用数据,建立了该飞机的年维修保障费用GM(1,1)模型,并对该模型的精度进行了检验,其精度为1级。实践证明利用该模型可以对未来几年内的维修保障费用进行有效预测。随着装备服役年限的增加,真实的维修保障数据会不断增加,所以,根据新的数据,还可以采取新陈代谢的方法,进一步改进模型,提高预测模型的准确性。装备自身的情况和日常的维护情况都会影响到装备的维修保障费用,装备和日常维护工作的情况都会随时间发生变化,因此,及时考虑新的数据是十分必要的。
参考文献
[1] 孙德全. 飞机维修品质与维修性设计[M ]. 北京: 中国人民解放军总后勤部司令部,1987.
[2] 邓聚龙. 灰色理论基础[M]. 武汉: 华中科技大学出版社, 2002.
[3] 刘建. 航天型号使用维修费用的GM模型估算方法研究[ J]. 航天工业管理,2004(11):17-20.
[4] 陈勇.民用飞机维修成本分析与评估 [D].南京:南京航空航天大学,2006.
[5] 范红军.军用飞机维修保障费用的GM(1,1)预测[J].微计算机信息,2011,27(5):126-127.
[6] 白暴力,杨琳.飞机维修费用估算的分析[J]. 空军工程大学学报: 自然科学版,2005,6(5):8-10.
责任编辑李思文
Application of Estimation with GM(1,1) Model for Aircraft’s Maintenance Cost
SUN Haixia,WEI Huakai,HAN Li
(Qingdao Branch, Navel Aeronautical Engineering Institute, Qingdao 266041,China)
Abstract:Based on the available maintenance costs data of a certain type airplane, a GM(1,1) model was applied by using the grey system theory to forecast maintenance cost and the accuracy of the model was demonstrated. It’s shown that the established model is accurate, available and is applicable to forecast the maintenance cost in several years later.
Key words:maintenance costs, GM(1,1) model, forecast
收稿日期:2014-03-14
作者简介:孙海霞(1979-),女,讲师,硕士,主要从事结构强度有限元分析及航空维修技术等方面的研究。
中图分类号:N 941.5
文献标志码:B
