一种近场屏蔽的基本模型及试验验证

丁永平，苏　醒，党　丽，郭艳辉

(中国兵器工业新技术推广研究所,北京 100089)



一种近场屏蔽的基本模型及试验验证

丁永平，苏醒，党丽，郭艳辉

(中国兵器工业新技术推广研究所,北京 100089)

摘要：随着对屏蔽理论的深入研究，屏蔽体的基本模型也在不断地发展。经典的Schelkunoff屏蔽定量测试方法是根据传输线理论来定量描述屏蔽效能的一种常用方法，但在实际应用中，研究者往往对其对于电场和磁场屏蔽的不同性产生质疑。通过对屏蔽效能描述方法的分析及对电场和磁场偶极子模型的研究和计算，建立了一种近场屏蔽的基本模型，利用该模型可清晰地描述屏蔽设备对外辐射发射与内部干扰源的对外辐射发射的依存关系，得出屏蔽体在远场对磁场和电场可进行同等衰减，而在近场对于低频磁场抑制更加困难的结论，并通过试验进行了验证，证明了Schelkunoff屏蔽分析方法在远场应用的正确性。

关键词：电磁屏蔽；基本模型；试验验证

1Schelkunoff屏蔽理论

通常来讲，屏蔽效能取决于屏蔽体的反射性损耗和吸收性损耗，屏蔽体的作用和屏蔽传输线模型如图1所示。最经典的定量测试方法是由Schelkunoff提出的[1]，是通过对屏蔽体和其周围环境介质(即图1所示的自由空间的特性阻抗(ZO、ZSh)和传播常数(ΓO、ΓSh))建模，并将传输线方程引入到屏蔽分析中。典型的有效屏蔽体通常具有比其周围环境介质更低的特性阻抗(ZSh)和更大的传导常数(ΓS)的实部，从而对入射电磁场产生较大的反射性和吸收性损耗，进而起到屏蔽的效果。传输线模型表明，屏蔽层对入射的磁场和电场衰减效果是相同的；但是在实际工程经验中，往往会觉得屏蔽强磁场干扰源要比屏蔽强电场干扰源困难得多。根据传输线理论，可以描述为屏蔽高阻抗场强比屏蔽低阻抗场强容易，因此对于研究Schelkunoff的屏蔽定量测试方法产生了诸多困惑。本文通过基本理论模型对其进行分析，并通过试验进行验证。

图1　屏蔽体的作用和屏蔽传输线模型

2屏蔽效能的描述方法

屏蔽效能定义为辐射源裸露状态的辐射场强与加屏蔽层后的对外辐射场强的比值，其场强测试如图2所示，其表达式为：

S(dB)=P1(dBm)-P2(dBm)

式中，P1为辐射源裸露状态的辐射场强；P2为加屏蔽层后的对外辐射场强。

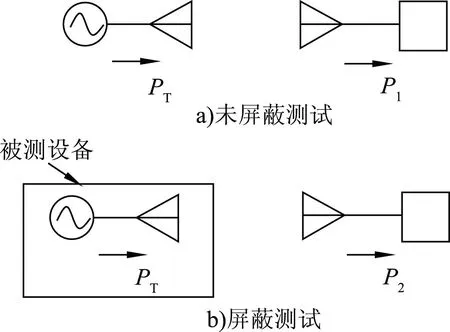
图2　屏蔽效能测试示意图

当屏蔽体物理尺寸比辐射源波长大时，屏蔽体的场强阻抗为377 Ω(ZF=E/H)，这相较于自由空间将起到效果，屏蔽效能S也会相应变大。当屏蔽体物理上小于干扰源波长时，场强阻抗相较于自由空间有可能会小很多，也有可能会大很多，这完全取决于屏蔽体内干扰源自身类型。在文献[2]中，屏蔽体可被视为辐射天线，并且提出了如下2条重要原则：1)当距离大于天线尺寸(即屏蔽体尺寸)2～3倍时，辐射场可用偶极子源系统来表示；2)场的本质是屏蔽体物理尺寸的一个函数，并且也是电磁激励的一个函数。由第1条原则可知，由已屏蔽的基本电场或磁场偶极子发射出的场可认为是衰减后的原始偶极子场；因此，在实际运用中可认为在电磁屏蔽模型中干扰源的基本发射是典型的基本环天线(磁场偶极子)，或者是短的电场偶极子天线。

3偶极子模型

3.1磁场偶极子模型

基本的磁场偶极子模型如图3所示。它的模型可用电流环来表示。偶极矩MH等于导通电流I与环形区域A的乘积。

图3　基本磁场偶极子模型

近场阻抗计算如下：Eφ=ωμIA/4πr2(θ=π/2)，Hr=IA/2πr3(θ=0)，Hθ=IA/4πr3(θ=π/2)，ZF=Eφ/Hθ=ωμr≅377r/(λ/2π)。

由上述计算可知，近场偶极子的场强阻抗ZF比远场阻抗(377 Ω)要小，并且当干扰源不断接近时其变得越来越小；因此，可定义磁场偶极子的近场特性为低阻抗场。

3.2电场偶极子模型

基本的电场偶极子模型如图4所示。它的模型可用一对具有相反极性，且其偶极矩ME等于电极间电量q和相互之间间隔L的乘积的间隔振荡电荷来定义。

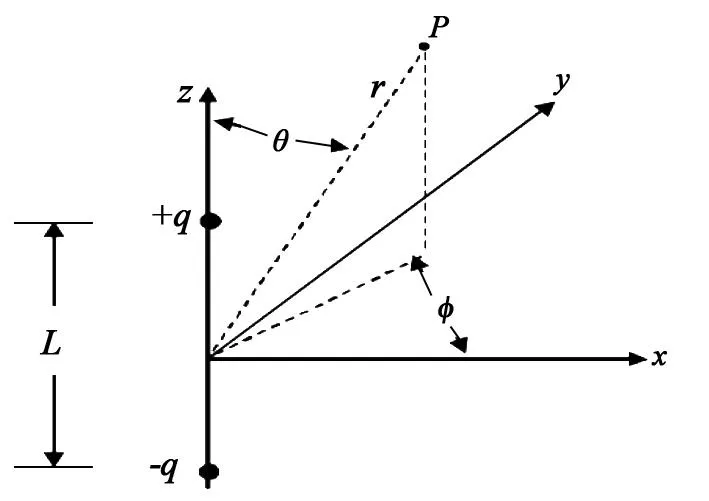
图4　基本电场偶极子模型

近场阻抗计算如下：Hφ=ωqL/4πr2(θ=π/2)，Eθ=qL/4πεr3(θ=π/2)，ZF=Eφ/Hθ=1/ωεr≅377λ/2πr。

由上述计算可知，近场电场偶极子的场强阻抗ZF比远场阻抗(377 Ω)要大，并且当干扰源不断接近时，其变得越来越大；因此，可定义电场偶极子的近场特性为高阻抗场[3]。

3.3偶极子模型的结论

由上述关于电场和磁场偶极子模型的方程式可得出如下结论：1)在电场偶极子和磁场偶极子的近场，场内的辐射分量φ和θ迅速衰减，并且远场比场内的衰减速度逐步减缓；2)在电场偶极子和磁场偶极子的近场，场内θ分量衰减速度比φ分量衰减速度快得多；3)在远场，场内φ和θ2种分量与r成反向衰减。

4基本屏蔽模型

4.1磁场基本屏蔽模型

基本的屏蔽电流环模型如图5所示。图5a所示的是未屏蔽的电流环区域A，电流为IL，磁场偶极子此时MH=ILA。图5b所示的是轴向屏蔽电流环，电流IL在屏蔽层上感应电流为ISh，它具有抵消由IL引起的磁场的趋势。其等效电路如图5c所示。

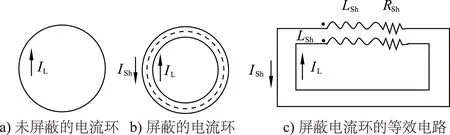
图5　屏蔽和未屏蔽的磁场偶极子模型

屏蔽层中的电流如下式：

(1)

但是，当LM=LSh时[4]，有：

(2)

在具有屏蔽的环内产生网络场的电流效应为：

(3)

屏蔽电流环的磁场偶极矩为：

(4)

磁场偶极矩MSh等于未屏蔽电流环的偶极距ILA，并随屏蔽的衰减因素(1/ (1+jωLSh/RSh))而改变。因此，屏蔽电流环的屏蔽效能为：

(5)

由式5可知，低阻抗偶极子随频率的降低屏蔽效能越高。

4.2电场基本屏蔽模型

基本的屏蔽电场偶极子电流环的模型如图6所示。图6a是一个伴有激励源的短线偶极子V。有效的偶极子电学长度大约是其物理长度L的一半，因此，具有的电场偶极矩为ME=qL/2=CWVL/2。

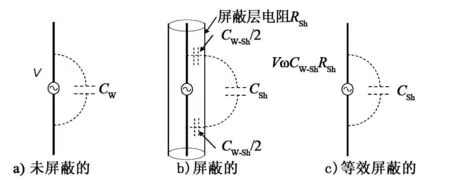
图6　屏蔽和未屏蔽的电场偶极子模型

图6b所示的是具有轴向屏蔽电场偶极子。导线与屏蔽层的耦合电容为CW-Sh，屏蔽层电流为ISh，屏蔽层等效电容为CSh，在图6c所示的等效电路中的屏蔽层等效电容的电压约为：

(6)

从而，屏蔽的电场偶极子的偶极矩等于：

(7)

当等效电容CW、CSh与导线及屏蔽层半径成对数函数关系时，它们几乎相等；当在式7中，将CSh用CW代替时，可见屏蔽的偶极矩和原始电场偶极矩相等，但其随衰减因素而变化。

具有屏蔽的电场偶极子的屏蔽效能为：

(8)

由式8可知，高阻抗偶极子在频率越低时屏蔽效能越高。

4.3基本屏蔽模型的结论

2种模型都揭示出屏蔽的磁场和电场偶极子仍保持它们各自未屏蔽基本偶极子的特性，只是具有衰减效应。典型屏蔽模型的屏蔽方程式和那些适用于球体屏蔽的理论模型的方程式形式相同[5-6]。

5模型的试验验证

图7、图8所示的数据图是一个实际具有环形激励源的屏蔽设备近场测试结果。测试设备为铝外壳，尺寸为31.5 cm×25.5 cm×13.5 cm。测试先将设备屏蔽，然后去掉屏蔽。在去掉屏蔽的测试中，取掉31.5 cm×25.5 cm的一面，而将一块约1 Ω/mm2的金属化塑料板作为盖子。具有相对高电阻的盖子可以减小测试的动态范围。

图7所示为设备的磁场近场发射测试，先裸露测试后屏蔽测试。从图7a和图7b中可以清晰地看出，在屏蔽前、后2种状态下的磁场衰减速率均为60 dB/decade，试验结果与方程式5中的计算结果基本一致，磁场衰减在低频段非常微弱，但随着频率升高衰减会变大。

图8所示的是设备的电场近场发射，先裸露测试后屏蔽测试。从图8a和图8b中可以清晰地看出，在屏蔽前、后2种状态下的磁场衰减速率均为40 dB/decade。在现有试验的测量精度条件下，对电场的屏蔽效能和对磁场的屏蔽效能(分别见图8c和图7c)的大体一致，这和从磁场偶极子模型得出的预测是一致的。

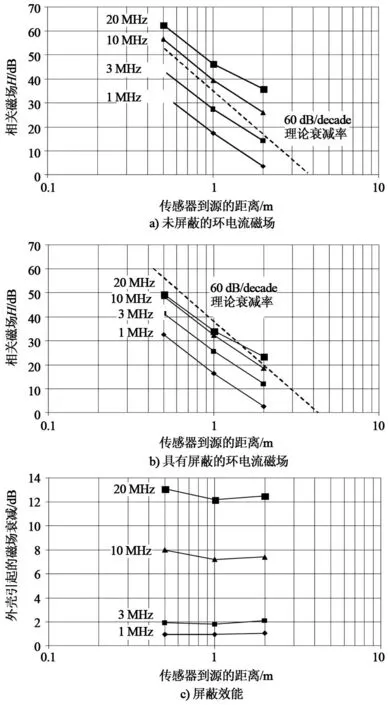
图7　环形源的磁场衰减

图8　环形源的电场衰减

6结语

本文对屏蔽电磁场偶极子的基本模型进行了介绍，并对其理论特性进行了推导。根据此模型，可以计算出屏蔽模型的近场辐射特性只是对未屏蔽偶极子源进行衰减，且通过模型可得出磁场和电场可由屏蔽进行同等的衰减，但衰减速率基本不同。通过对具有环形激励源的屏蔽设备进行近场测试的结果表明，该近场屏蔽模型与实测数据基本吻合，能够准确描述近场屏蔽效能。说明在近场低频磁场比高频电场更加难抑制，同时验证了Schelkunoff屏蔽分析方法在远场应用的正确性。

参考文献

[1] Schelkunoff S A. Electromagnetic waves[M].New York：D.Van Nostrand Company, Inc., 1948.

[2] 杨克俊.电磁兼容原理与设计技术[M].北京：人民邮电出版社，2004.

[3] 王岩.用传输线输入阻抗原理确定屏蔽提屏蔽性能[D].北京：北京邮电大学，2007.

[4] Mohr R J.Coupling between lines at high frequencies[J].IEEE Trans. On EMC, 1967, 9(3):127-129.

[5] Miller D A， Bridges J E. Review of circuit approach to calculate shielding effectiveness[J].IEEE Trans. on EMC, 1968,10(1):52-62.

[6] Wheeler H A.The spherical coil as an inductor, shield, or antenna[J], Proc. IRE, 1958, 46(9):1595-1602.

责任编辑马彤

A Fundamental Model for Near-field Shielding and Verification Test

DING Yongping, SU Xing, DANG Li, GUO Yanhui

(Advanced Technology Generalization Institute of CNGC, Beijing 100089, China)

Abstract：The fundamental models for shielding enclosure are developing with constant researches on the shielding theory. The classic approach for the quantitative treatment is that presented by Schelkunoff approach by employed transmission line equations in shielding analysis. But in practical application, the difference between electric field and magnetic field shielding is often questioned. Through the analysis of the method of shielding effectiveness and the research, and the calculation of electric and magnetic dipole model, a basic model for near field shielding could illustrate the interdependence of emissions from the shielded enclosure and the basic source of emissions within the enclosure. The conclusion shows that the magnetic and electric field can be equally attenuated in the far field, but in the near field shielding the magnetic field is more difficult. And a verification test is designed to verify the conclusion of the basic model, and prove the correctness of Schelkunoff approach to shielding analysis which is often questioned.

Key words:electromagnetic shielding， fundamental models， verification test

收稿日期：2015-10-09

作者简介：丁永平(1983-)，男，高级工程师，主要从事电磁兼容性测试技术，复杂电磁环境分析及防护等方面的研究。

中图分类号：TM 15

文献标志码:A