基于CAM的空间投影曲线槽的加工工艺研究

宁　栋，贡喜东，赵海峰

(西安近代化学研究所，陕西 西安 710065)



基于CAM的空间投影曲线槽的加工工艺研究

宁栋，贡喜东，赵海峰

(西安近代化学研究所，陕西 西安 710065)

摘要：研究了在拟合曲线回转体零件上加工等壁厚槽的工艺过程。利用数学建模方法建立了空间曲线方程，并应用CAM软件根据相贯曲线在空间投影的变化找出实际加工点的坐标。使用相对应的工装解决了相贯曲线在空间投影后曲线槽的加工问题，提出了合理、有效的加工方案，提高了加工精度，满足了产品图样技术要求。

关键词：拟合曲线槽；坐标点；CAM；相贯曲线空间投影

筒体零件是某产品的重要件(见图1)，其内、外型均是由N个坐标点拟合而成的曲线回转体，等壁厚，其中外曲面已在数控车床上加工完成。产品要求在拟合曲线回转体外圆周上加工多条1.5 mm宽、10 mm深的均布曲线槽。该曲线槽与轴线夹角为5°，横贯外曲面整个轮廓。加工后的槽深在回转曲面的不同位置要求保持一致，由于原始坐标点发生了变化，由此形成了新的空间相贯拟合曲线。在用立式加工中心进行铣削时，如再用图样给定的原始曲线坐标点编程加工，则加工后的槽深、壁厚尺寸就会发生较大的变化，偏离图样设定的技术指标；因此，如何找出新的相贯拟合曲线在空间的坐标点是曲线槽加工工艺研究的关键所在。通过一年多的反复研究、实践，在加工方式、工艺改进等多方面做了大量的研究工作，解决了筒体曲面与平面相贯后在空间投影形成的新的拟合曲线槽坐标点的问题，使产品加工质量更加稳定，满足了设计要求。

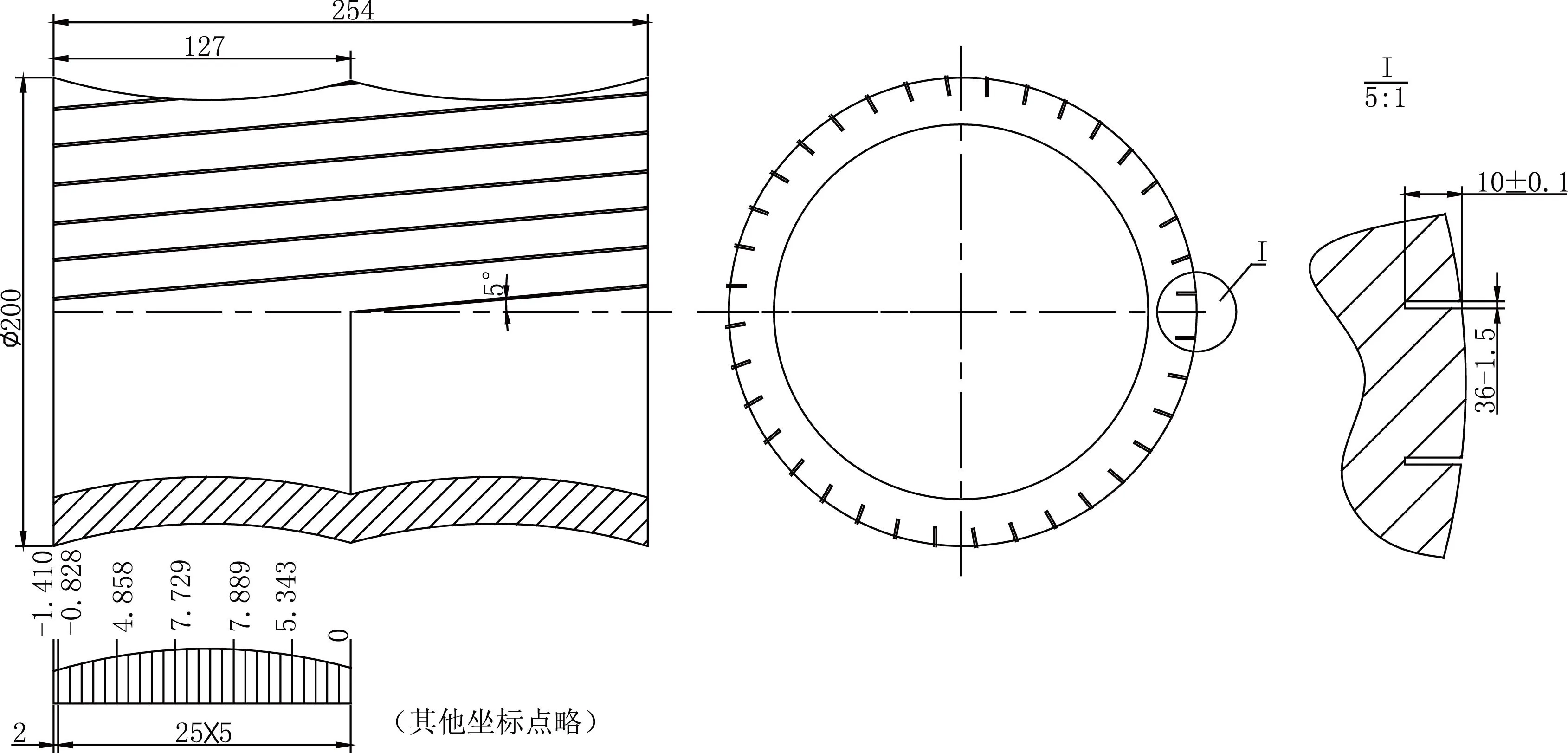
图1　零件简图

1建立曲面上曲线的数学模型

在CAD/CAM领域，常利用参数形式表示曲面。在给定的坐标系下(不一定是直角坐标系)，1个曲面可表示为2个变量的单值函数，即S(u,v)=0,(u1≤u≤u2，v1≤v≤v2),参数偶(u,v)和曲面上的点是一一对应的。

曲面上曲线(见图2)的加工，是当曲面整体已加工完成时，对曲面上局部待加工区域内用投影法确定刀具轨迹进行插补计算。由图2可以看出,待加工曲线就是将参考坐标系下某一空间矢量作为投影方向，把直线族在曲面上的投影曲线作为实际的刀具路径[1]。

图2　曲面上的曲线

1.1曲线拟合

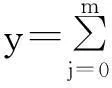
以表1坐标点为例，应用MATLAB软件对其做二项式拟合：f(x)=a1x2+a2x+a3。

表1　曲线拟合数据　(mm)

拟合的MATLAB代码如下：

x=[-127.486 -120 -95 -70 -45 -20 0];

y=[0.789 1.147 5.838 7.908 7.421 4.363 0.789];

A=polyfit(x,y,2);

xx=-127.486:0.001:0;

z=polyval(A,xx);

plot(x,y,'k+',xx,z,'r')[3]

程序执行后，在MATLAB Command Window对话框中可得：a1=-0.001 8,a2=-0.226 4,a3=0.747 0。

拟合结果如图3所示。

图3　拟合的曲线

1.2旋转曲面方程

设旋转曲面的母线为：

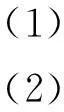
设旋转轴过点(a，b，c)，且方向向量为s=(l，m，n)，则其对称式直线方程为：

(3)

取一圆族，使它们的圆心在旋转轴上，且圆所在的平面与旋转轴垂直，则此圆族方程为：

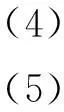
式中，R、p是2个变化的参数，R是球面半径，2个参数的连续变化形成了一圆族。

从式1～式5中任意取3个，联立求出x,y,z,代入其余的一个即得：

H(R,p)=0

(6)

再由式4～式6，得旋转曲面方程为：

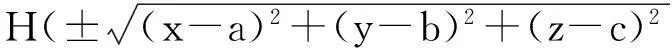
lx+my+nz)=0

(7)

那么，以y=f(x),z=0为母线，以X轴为旋转轴，所产生的旋转曲面方程为：

(8)

1.3投影曲线方程

投影曲线即旋转曲面与平面的交线(见图4)。根据题意知，与X轴夹角为α，平行于Y轴，且过点P0(a,0,0)的平面的法向量式方程为：

图4　交线的形成

上述旋转曲面与该平面的交线(即欲加工目标曲线)，其解析式可表示为：

可以看出，刀具路径是由这族直线族沿一空间矢量投影到曲面上形成的[4]。

2应用CAM进行曲线坐标点的补偿与修正

空间曲面与平面的交线是空间平面曲线，对于数控系统，插补空间曲线难度较大，铣刀插补点的求解较为复杂，工艺上也难以进行加工。方案初期考虑选用硬质合金φ1.5mm键槽铣刀，利用立式加工中心四轴联动，分层加工该曲线槽；但由于此槽较深，刀具耐用度不高，磨损严重，加工初期此方案即被否定。后来，经过反复实践，发现利用高速钢锯片铣刀，根据图样要求将零件轴线倾斜5°，使待加工曲线与坐标系X轴平行，在等高平面下进行插补运算，这样简化了插补点的求解，满足了窄槽与轴线夹角5°的设计要求。

党的十九大把习近平新时代中国特色社会主义思想确立为我们党必须长期坚持的指导思想，实现了党的指导思想的又一次与时俱进。习近平新时代中国特色社会主义思想，集中体现了十八大以来我们党理论创新、实践创新、制度创新的丰硕成果，在理论和实践上实现了新的突破，具有重大而深远的政治意义、理论意义、实践意义、世界意义。

曲线的投影及比较如图5所示，曲线1为图样给定的坐标点拟合形成的曲线，曲线2为与轴线倾斜5°的直线，曲线3为待加工轨迹曲线。从图5中可以看出，待加工曲线3与图样给定的曲线1有偏差，所以在加工曲线槽时需要对已知原坐标点进行补偿与修正。在研究中，应用CAD/CAM软件进行实体的生成和曲线的投影，以大量直线段来逼近投影曲线，利用数控系统的插补功能，找出新曲线的坐标点，从而加工出曲线。

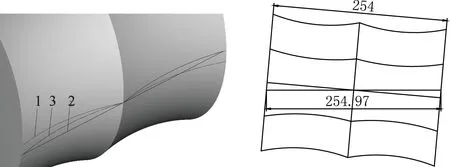
图5　曲线的投影及比较

MasterCAM软件是美国CNCSoftware公司开发的CAD/CAM系统，是目前国内广泛应用的CAD/CAM软件之一。其主要特点是操作简单、易学，且自带多种标准的后置处理，方便自定义刀具库[5]。本文以该软件为例进行说明,具体步骤如下：1)开启新档，在构图面XOY平面依次输入给定坐标点，绘制曲线1；2)以X轴为旋转中心，以曲线1为母线旋转360°，生成实体；3)在XOZ平面上绘制一条与轴线夹角为5°直线2；4)选择“绘制—曲线—曲面曲线—投影线”，分别选择直线2与实体，在构图面XOZ平面内向实体曲面进行投影，生成曲线3，曲线3即为目标曲线。

通过5°直线建立一个新平面，在此平面中建立新坐标系，与原给定坐标数值进行比较，结果如图6所示(因曲线两边对称，在此仅以一半为例进行说明)。

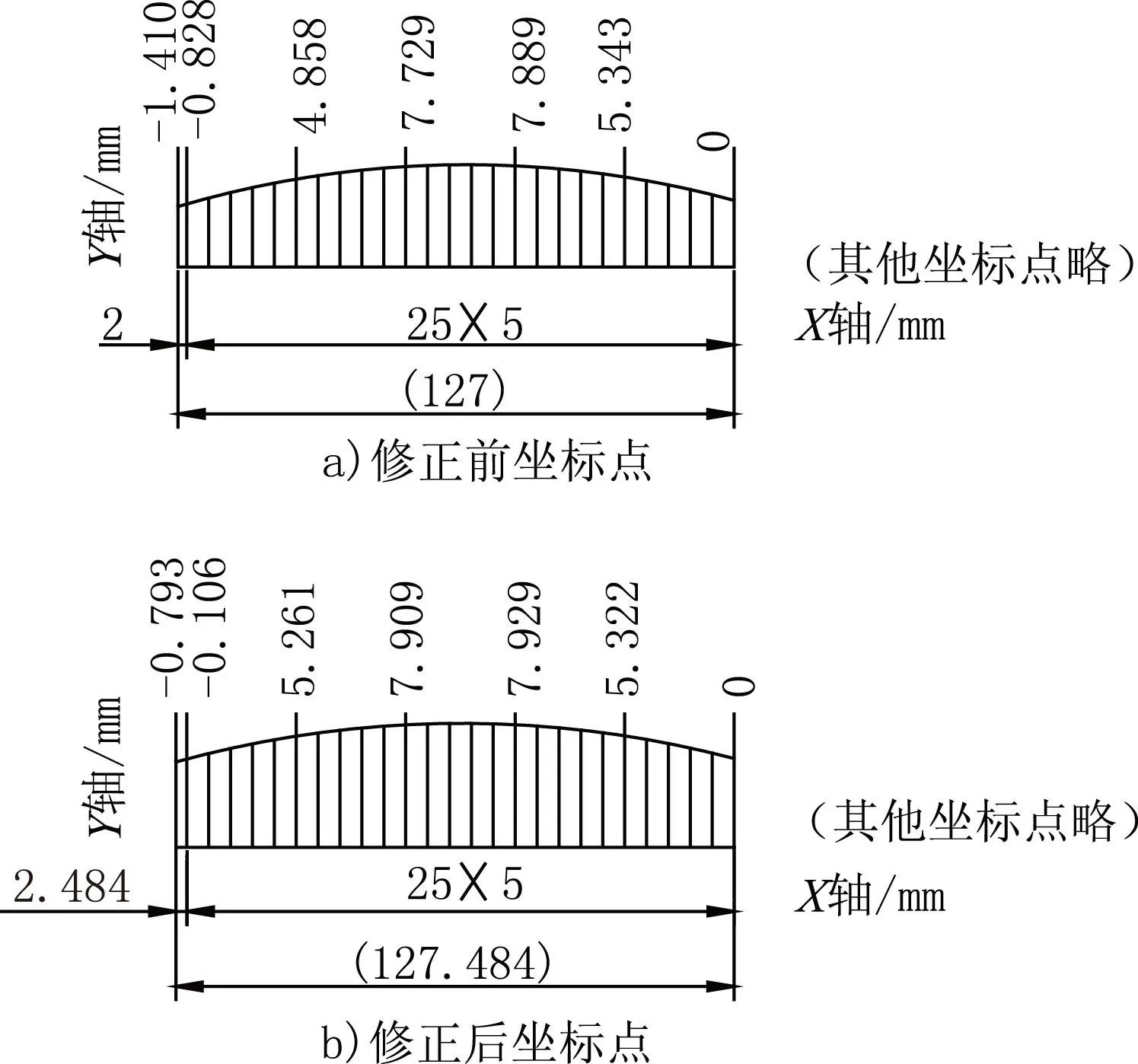
图6　曲线的修正与补偿(一半)

经测量，新生成的目标曲线3长度为254.97mm,比原给定曲线254mm增长了0.97mm(见图5)。由此可见，在铣曲线槽时，如果直接用原给定坐标点进行编程，则加工的结果是偏离图样要求的。

3工件坐标系的设定

经分析，筒体零件在曲线槽加工时需以内孔定位，运用心轴一夹一顶的装卡方式来限制工件的5个自由度，同时与车削外曲面基准统一。设备选用美国Hardinge立式加工中心，为简化编程与加工，制作了可调式倾斜工作台(见图7)。加工时，工作台调整为5°，并打表找正，锁紧，使待加工曲线位于水平面。采用具有良好韧性及耐用度的高速钢涂层锯片铣刀，沿目标曲线单向多次切削实现[6]。

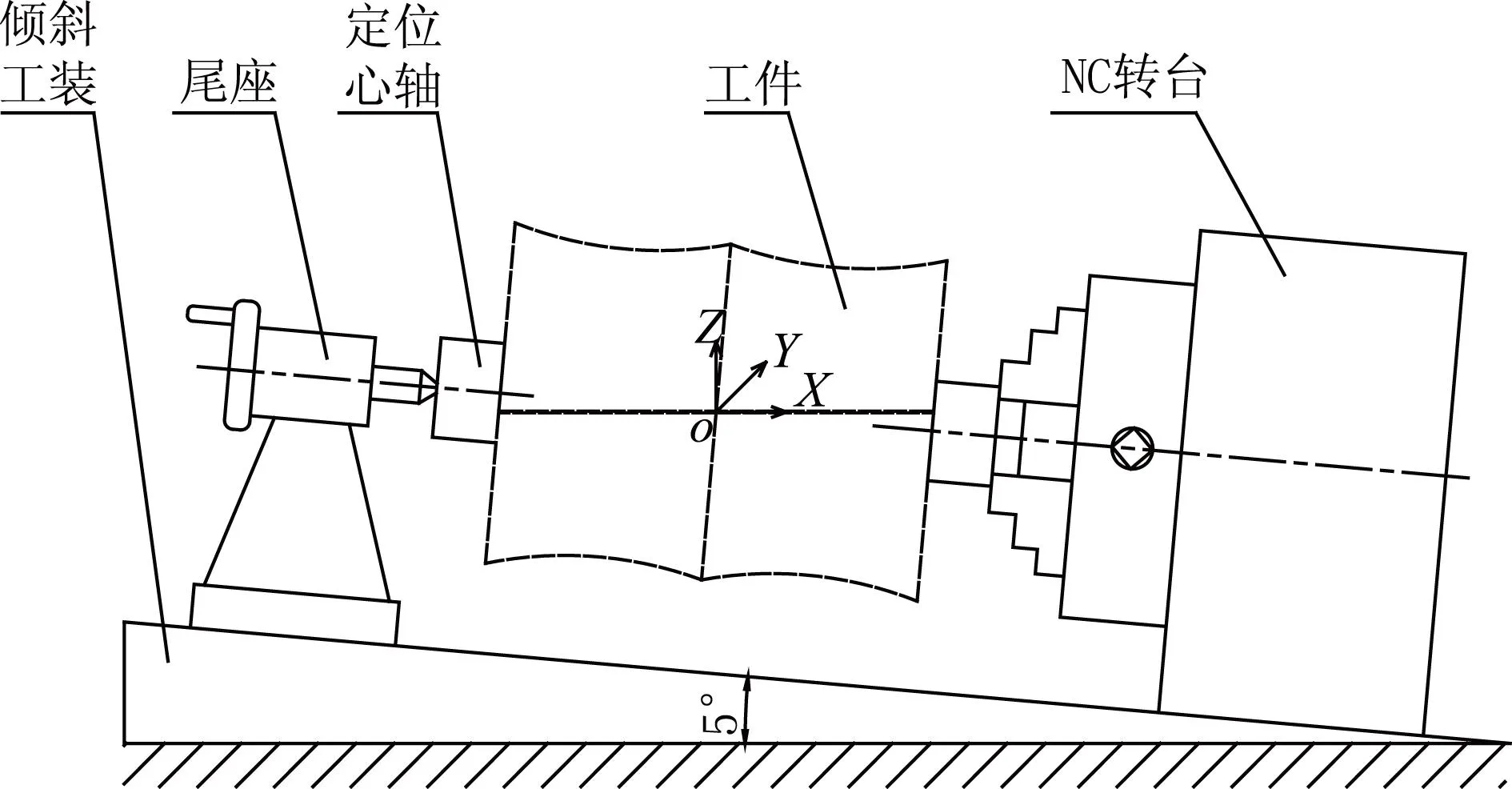
图7　可调式倾斜工作台示意图

工件坐标系的设定如图8所示，工件坐标系原点设置在工件轴向中心，即距端面127mm处。

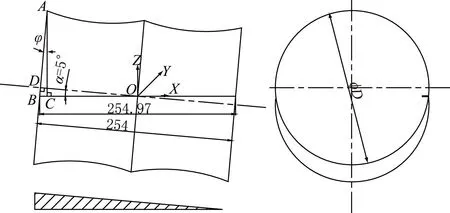
图8　工件坐标系的设定

在开始加工前，采用如下方法进行对刀。

1)X方向：由于工件坐标系设置在工件中心位置，X方向直接对刀不便操作。

由图8可知，在ΔDBO中：DB/DO=tanα，DB=127tan5°=11.11 (mm)；DO/BO=cosα，BO=127/cos5°=127.485 (mm)。在ΔABC中：BC/AB=sinφ，BC=(D/2+DB)sinφ=9.684 (mm)，CO=BO-BC=117.801 (mm)。

使用寻边器在端面靠近A点处对刀，得到CO的距离，这样即可完成X方向坐标系的设置。

2)Y方向：工件装夹之前，使用标准棒进行转台与顶尖的校正，并用寻边器对标准棒进行分中，将机械坐标值输入G54坐标系中，完成Y方向坐标系的设置。

3)Z方向：在MDI状态下，执行G54G0Y0指令，将工件移至G54坐标系下Y方向工件中心位置，刀柄夹持小定心钻，主轴正转，在工件上表面X方向曲线拐点处轻点一标记小孔(随后加工曲线槽时该孔被切削掉)。然后第四轴转动90°至操作者面前位置，装卡锯片铣刀，手轮状态下移动Z轴，目测刀片中心与标记小孔重合。记录并输入Z轴机械坐标值，完成Z轴的工件坐标系的设置。

工件坐标设置完成后，在MasterCAMV9.0软件中，对于生成的目标曲线进行CAM刀路编程及后置处理，生成刀具路径(见图9)。

图9　生成的刀具路径效果

上述方法可以实现简单对刀，当首条曲线槽试切完成后，需进行槽深测量，如发现槽深尺寸深浅不一，可利用FANUC系统中的旋转指令(G68X_Y_R_)进行曲线的旋转,或运用坐标系的偏移进行微调，直至整个槽深均匀，满足设计要求。

4结语

通过研究并验证，用上述方法进行加工，曲线的轮廓与槽深全部合格，满足了图样的技术要求。上述应用CAM软件建模进行曲线投影的加工方法可以推广至其他回转体曲面，为同类产品的加工工艺提供了范例。

总而言之，曲面上的投影曲线深槽加工是一个复杂的过程，涉及到机床的几何精度、工件的定位误差和数控系统的插补精度等各个环节。要实现此类零件的高效率、高精度及低成本的加工，应从数控加工工艺路线、切削参数以及选择高性能刀具等方面进行优化及试验研究，从而满足此类产品批量生产的需要[7]。

参考文献

[1] 孟书云，赵东标.参数曲面上投影曲线的直接插补算法[J].华南理工大学学报，2006,34(2)：88-91.

[2] 王能超.数值分析简明教程[M].北京：高等教育出版社，2001.

[3] 张志涌，等.精通MATLAB[M].北京：北京航空航天大学出版社，2009.

[4] 高红铸，王敬庚，傅若男.空间解析几何[M].北京：北京师范大学出版社，2007.

[5] 龚环球.MasterCAM软件在航空发动机零部件数控加工编程中的应用[J].新技术新工艺，2013(3)：11-14.

[6] 吴拓.现代机床夹具设计[M]. 北京：化学工业出版社，2008.

[7] 杨金发，叶洪涛，田晓龙，等.薄壁斜深槽加工技术研究[J]. 金属加工，2012(2):43-45.

责任编辑郑练

The Research on the Processing Technology of the Space Projection Curve Groove based on CAM

NING Dong，GONG Xidong，ZHAO Haifeng

(Xi’an Modern Chemistry Research Institute, Xi’an 710065, China)

Abstract：The processing technology of equal-thickness wall groove with fitting curve on the turning pares with fitting curve is introduced. The space curve equation is established by the method of mathematics modeling, and the coordinate of the practical processing point is found from the space projective transformation of intersection by CAM software. The processing technology curve groove induced by the space projection of the intersection is settled and more proper and effective processing program is proposed by improving the processing accuracy.

Key words:equal-thickness wall groove with fitting curve, coordinate of the practical processing point, CAM, the space projection of the intersection

收稿日期：2015-04-28

作者简介：宁栋(1982-)，男，技师，大学本科，主要从事CAD/CAM数控加工工艺等方面的研究。

中图分类号：TG 659

文献标志码:A