基于分数阶PID控制器的储气罐恒压控制
2015-03-15麦云飞
王 杰,麦云飞
(上海理工大学机械工程学院,上海200093)
0 引 言
随着科技的进步和对控制品质要求的提高,控制精度和鲁棒性要求更高,控制效果要求更好,在运行要求更稳定、可靠、准确的场合下,传统PID控制的缺陷越来越凸现出来。因此,寻求一种切实可行、效率较高的算法就显得尤为重要。本文首先对分数阶PID算法和传统PID算法作了简单的对比,凸显了分数阶PID算法的优越性,然后给出其简化工程算法,将其运用在储气罐恒压控制系统中,在最优传统PID参数的基础上运用分数阶PID的工程算法,最后对比了两者的实际控制效果。
1 分数阶PID算法
分数阶PID算法在时域中的表达式为:

由G-L分数微积分定义[1]得:

式中,
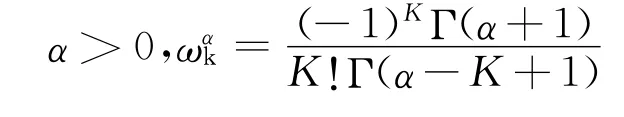
权系数ωαk可视为幂级数(1-x)α在原点的泰勒展开式的系数:
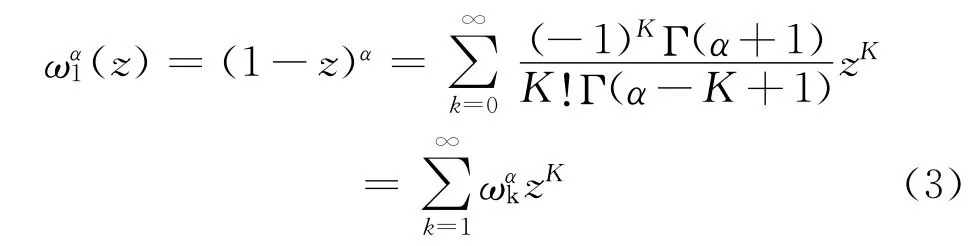
对于G-L分数微积分的2~6阶近似,Lubich给出了如下结论:一阶导数的n阶近似表达式可用(n+1)个点的后向差分表示,同样,(n+1)个点的后向差分表达式的p次幂可以表示p阶导数的n阶近似,则有:
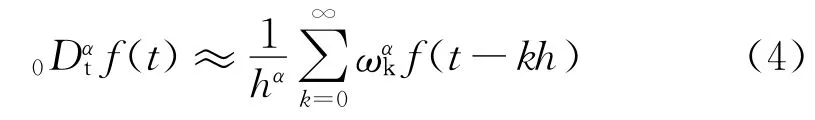
令采样周期为T,式(3)经Z变换得:

时间离散化得到分数阶PID数字实现表达式如下:

式中,Um为分数阶PID控制器的输出;ym为反馈值;rinm为定义目标值;λ为积分阶次系数;μ为微分阶次系数。
从上式可见:分数阶PID比传统PID多了2个可调参数λ和μ,而且阶次是可以任意选择的,因而更具灵活性,选择范围也更大。
2 分数阶PID改进算法
由分数阶PID控制器的表达式可知:由于引入系数dj、qj,并且dj、qj是一个与运算次数j相关的表达式,无法通过递归法消去之前的误差e。直接将其表达式数字化实现是不可行的,因为任何微处理器的资源是有限的,长时间运行必定会发生溢出的现象;由于分数阶PID的记忆性,每增加一个e对于积分项和微分项,微处理器就需要多计算一次,长时间使用微处理器,计算时间就会比初始状态增加时间Δt,这违背步长h一致原则[2]。
综上所述,直接将分数阶PID控制器的数字实现表达式运用于工业微处理器中不可行,因此必须对公式进行简化。
对于积分环节而言,整数阶PID对以前任何时刻采样点的记忆性相同,而分数阶积分只与当前时刻较近的有限项采样点值有明显关系。通过观察分数阶PID表达式的积分项与微分项发现:当λ=-μ的时候积分项表达式ui=ud,所以推测:分数阶PID积分项和微分项只与当前时刻较近的有限项采样点值有明显关系。
由此提出了短记忆分数阶PID算法:取有限项。
具体算法如下:以取n+1项为例进行说明(记忆长度L为n+1)。

当m<n的时候按原式计算,当m≥n的时候分数阶控制器输出Um可通过取最近的n项误差e和从n+1项以q0、d0作为起始项至qn、dn为止的微分与积分系数计算得到。
3 分数阶PID在储气罐恒压控制系统中的应用
储气罐恒压控制系统由控制器、压力传感器、信号调理电路、比例阀、储气罐、气源等组成,其系统框架如图1所示,系统原理框图如图2所示。储气罐的压力值由压力传感器实时采集并转换为模拟量信号,经控制器内部计算转换为压力反馈信号。控制器读取储气罐实际压力和设定压力后,交由控制器算法在线运算,计算出控制量,将控制量输出到比例阀放大器,实时改变比例阀阀芯开口大小跟开口方向,实现储气罐压力实时跟随设定压力。
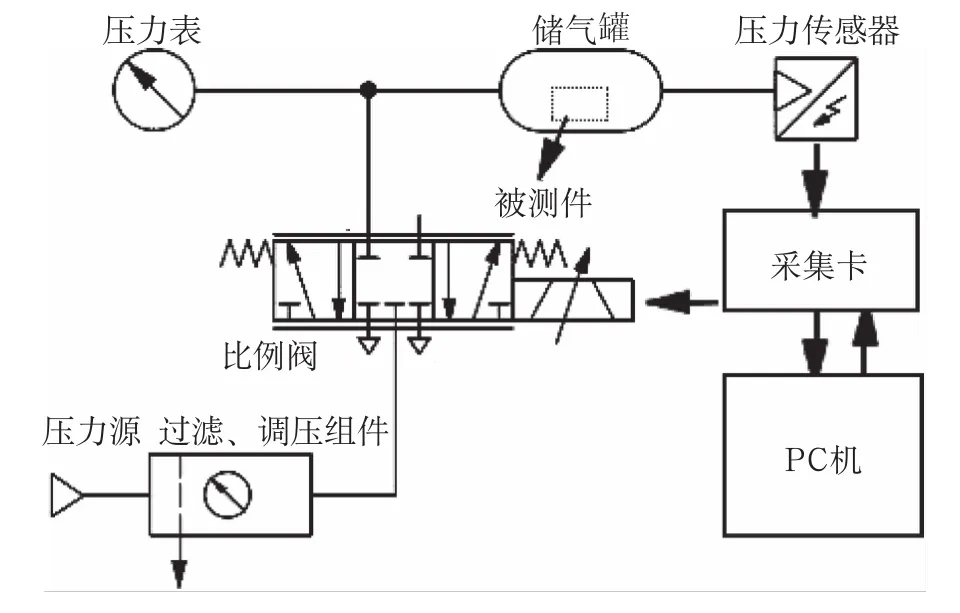
图1 储气罐恒压控制系统框架图
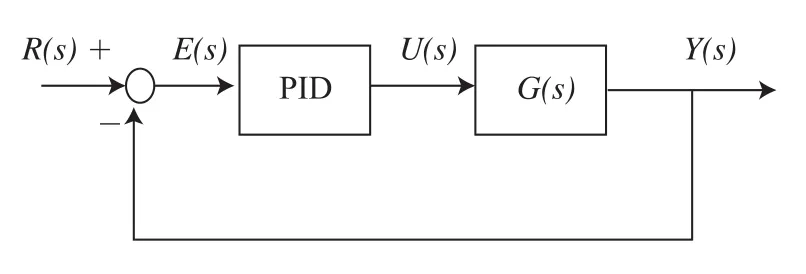
图2 储气罐恒压控制系统原理框图
3.1 系统工作阶段分析[3]
(1)充气阶段
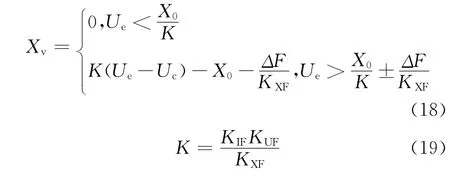
式中,Ue为输入电压信号;Uc为比例阀阀口全关时的输入电压;Xv为阀芯位移;X0为反馈弹簧预压缩量;ΔF为干扰力;K为比例增益;KIF为比例电磁铁的电流-力增益;KUF为比例放大器的电压-电流增益;KXF为反馈弹簧的弹性系数。
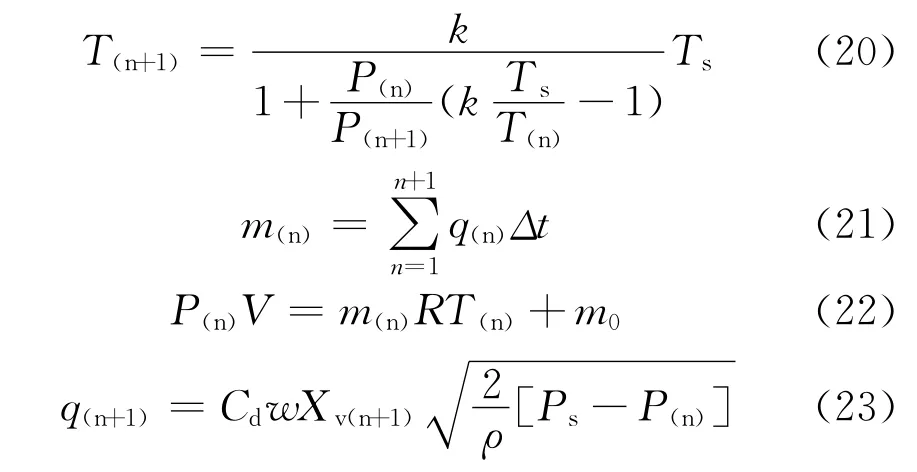
式中,T为储气罐内气体温度;P为储气罐内气体压力;Ts为气源温度;K为绝热系数;m为储气罐内气体质量;m0为储气罐内原有气体质量;q为比例阀阀口流量;Δt为采样间隔;V为储气罐体积;R为气体常数;Cd为流量系数;w滑阀节流窗口面积梯度;Ps为气源压力;ρ为气体密度。
(2)放气阶段

(3)比例阀阀口关闭阶段
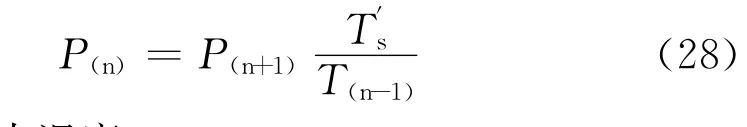
式中,T′s为室内温度。
由系统工作阶段分析可知:温度、压力、空气量三者之间互相影响,因此该系统属于非线性系统。本文分别用传统PID和分数阶PID来进行压力控制,对两者实际控制效果进行比较。
3.2 测试
测试步骤如下:
(1)寻优[4]
调整传统PID参数,使其处于最优状态。
(2)对比
a.取相同参数的分数阶PID对比,不同记忆长度的分数阶PID进行对比。
图3中的曲线为跟随频率为0.1 Hz,振幅为1,偏差为3,占空比50%的方波信号所得。

图3 不同记忆长度的分数阶PID对比曲线
整理曲线和实验数据得表1。

表1 a对比曲线数据对比图
对比结论:短记忆分数阶PID会引入稳态误差;随着记忆长度L的增加,分数阶PID稳态误差逐渐下降;上升时间对记忆长度L不敏感。
取相同Kp,Ki,Kd的整数PID与分数PID控制器曲线对比。
b.对比所得曲线如图4、图5所示。

图4 传统PID压力响应曲线

图5 分数阶PID压力响应曲线

表2 b对比曲线数据对比图
对比结论:分数阶PID比传统PID上升时间tr明显减少;随后进行的大量随机试验证明采用分数阶PID控制算法,系统的可靠性、适应性得到显著提高,很好地实现了非线性控制。
4 结束语
分数阶PID更具灵活性,选择范围更大,在传统PID调至最优后,用短记忆分数阶PID可以进一步将其优化,响应速度能够大幅度提升。短记忆分数阶PID算法的提出有利于突破传统PID的局限性,具有很好的发展前景。
[1]PODLUBNY I.Fractional-order systems and PIλDμ-controllers[J].IEEE Trans on Automatic Control,1999,44(1):208-214.
[2]高建龙.分数阶PID控制器在伺服系统中的应用及实现[D].南京:南京理工大学,2013.
[3]黄友锐.曲立国.PID控制器参数整定与实现[M].北京:科学出版社,2010.
[4]张 超.多变量系统分数阶控制器的设计[D].南京:南京信息工程大学,2011.
[5]任彦硕.自动控制系统[M].北京:北京邮电大学出版社,2006.
