基于递推最小二乘卡尔曼滤波方法的模糊度解算*

徐冠楠 汪 捷

(海军工程大学导航工程系 武汉 430033)



基于递推最小二乘卡尔曼滤波方法的模糊度解算*

徐冠楠 汪 捷

(海军工程大学导航工程系 武汉 430033)

针对北斗动态定位,通过使用递推最小二乘方法,采用扩展卡尔曼滤波的方法估计模糊度浮点解,实现了利用多历元载波相位观测信息求解整周模糊度。通过模拟北斗观测数据进行仿真,可以得出扩展卡尔曼滤波的方法精度高,适合动态定位解算。

北斗动态定位; 最小二乘; 扩展卡尔曼; 整周模糊度

Class Number TP301.6

1 引言

Kalman滤波是目前动态导航定位中最常用的方法,其特点是一种时域滤波方法,引入了状态空间概念,算法采用递推形式,即利用系统的状态转移方程,由参数的验前估计和新的观测数据进行状态参数的更新,递推估计新的状态估值。在高精度动态定位中,通常是对位置等运动参数进行估计,而不对它们的误差进行估计,由于解算中需要用到载波相位观测数据,因此待估状态向量不仅仅包含位置和速度等载体运动参数,同时还包含模糊度向量参数。

2 Kalman滤波原理

2.1 Kalman滤波的通用模型

Kalman滤波是一种基于状态模型解决最优估计,能够使用递推方式的数据处理方法。Kalman滤波的方程表示如下:

xk=φk-1,kxk-1+Γk-1wk-1
Lk=Akxk+vk

(1)

式(1)中,xk是系统的n维状态向量,包括用户位置、速度、加速度、整周模糊度、电离层延迟、对流层延迟等待估参数。wk-1是系统的q维过程噪声向量,Γk-1是n*q维干扰系数矩阵,φk-1,k是系统的状态转移矩阵,Lk是观测值向量,Ak是设计矩阵,vk是观测噪声。系统的观测噪声和过程噪声都是均值为零,且不相关的白噪声。其统计特性表示如下:

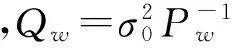
2.2 扩展Kalman滤波(EKF)

由于Kalman滤波适用于线性观测系统,但是在北斗动态定位中,由于观测方程式是非线性的,需要采用一种新的滤波方法,即本文采用的扩展Kalman滤波方法进行结解算。其总体思路是将非线性的函数通过泰勒展开并截断高阶项将其线性化之后再进行滤波。首先,采用扩展Kalman滤波方法构造系统方程和测量方程,利用条件平差方法进行推导。扩展Kalman滤波的观测方程在某一点处线性化可以表示为

进一步简化可以得到:

Lk=Hkxk+vk

式中的xk为Δxk,于是上式可以改写为

由上述分析可以得到此时的预估残差权逆阵为

计算增益矩阵Kk:

计算出最终的滤波解:

3 北斗动态定位模型与解算

针对实际北斗动态定位情况,利用扩展Kalman滤波结合定位中观测方程与状态方程作解算。

3.1 观测方程

设tk历元,参考站r和流动站p都观测到了m颗卫星,每个测站的双频伪距与双频载波观测量已知,分别双差,得到双差观测量,设参考卫星为k,则动态定位的状态向量为

在动态定位中,观测量Lk为

函数f(xk)的表达式表示为

f(xk)=[fφ1fφ2fR1fR2]T

其中:

由f(xk)可以得到Hk的表达式:

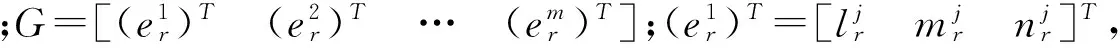
双差观测量的方差-协方差阵可表达为

其中:

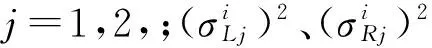
3.2 状态方程

在实际定位中,假设在某一历元时刻观测了m颗卫星,状态向量的维数为n,状态转移矩阵φk-1,k的表达式可以写为

式中的Ik为K阶单位矩阵,Δt为观测数据的采样间隔。

矩阵Γk-1的表达式为

动态噪声的方差协方差阵表示为

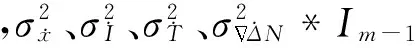
4 算法仿真与分析

接下来将上述扩展卡尔曼滤波方法进行仿真,从而便于对算法进行分析,证明其滤波定位精度可以为后续的整周模糊度解算提供初始值。

由于目前北斗尚未有公开的双频观测数据,为了保证算法的有效性,下面的仿真将用模拟的北斗观测数据以及真实的GPS数据来分析算法的效果。

4.1 卫星星历模拟仿真

对一个观测点的可见数目进行仿真。如图1所示,在连续3000个历元中,可见的卫星数目不断发生变化,由于只有当卫星数目值大于等于4的时候才能完成解算。

4.2 用户运动轨迹的模拟

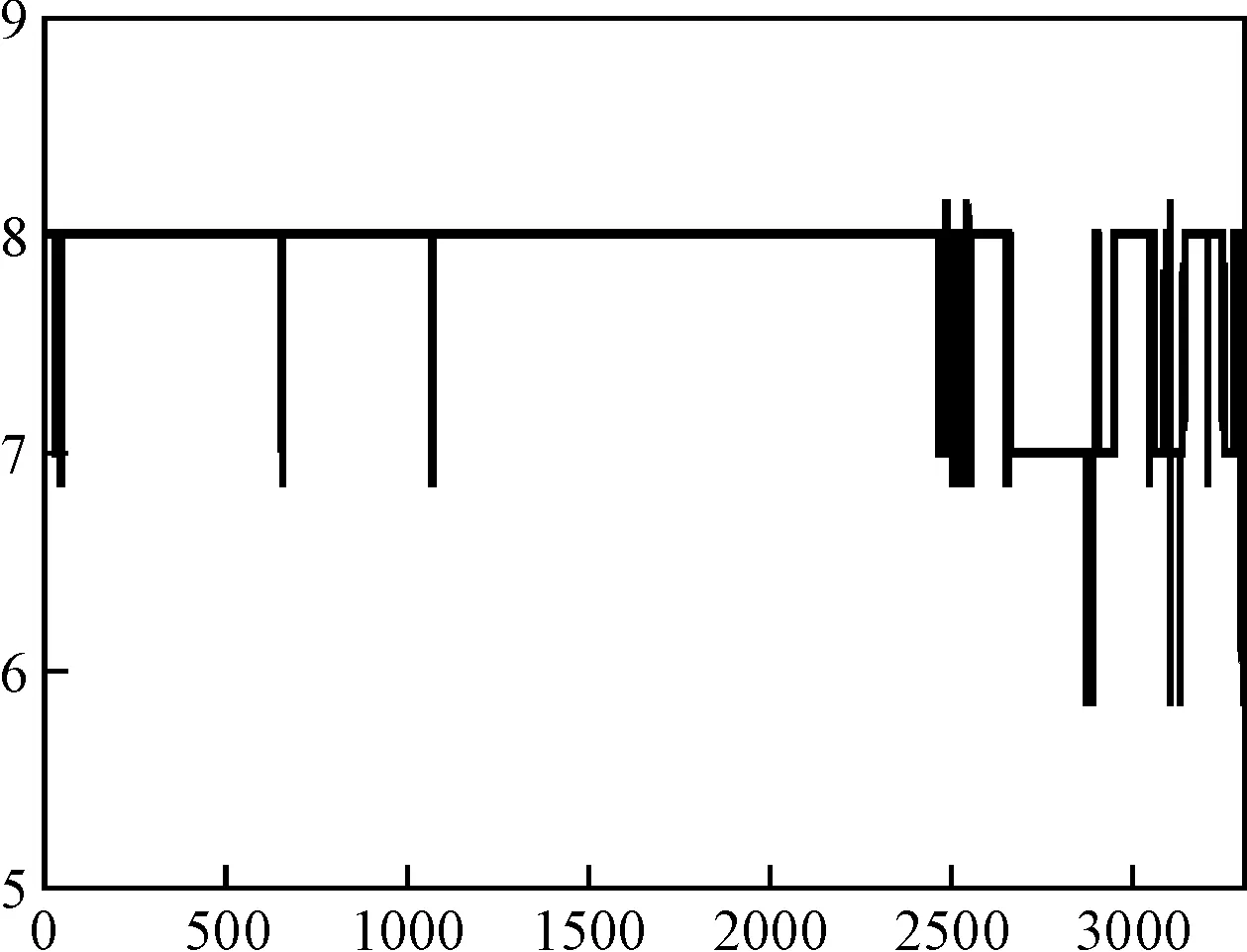
图1 可见卫星数目仿真

图2 飞行器运动轨迹模拟路线

4.3 观测数据模拟方法

在数据模拟一块,首先可以模拟出无噪声的载波相位测量值,再加入高斯白噪声等噪声,这样就产生了北斗导航系统的载波相位测量值。同样的对于北斗系统伪距测量值,模拟思路大致一样,首先模拟出无噪声的伪距测量值,然后加入钟差等各种误差的影响,在此基础上再加入多种噪声,这样就产生了北斗导航系统的伪距测量值。

图3 观测数据模拟方法

4.4 滤波定位算法仿真与性能分析

利用已有的模拟数据进行算法仿真,结果如表1所示。在东向和北向给以初速度,观测扩展卡尔曼滤波法在滤波前后各方向的误差变化情况。

表1 模拟北斗观测数据下的EKF定位误差方差

通过观测图可知,EKF定位滤波算法的在减小误差以及适应性方面很显著。在0～100历元时刻里,东向误差又滤波前的-50m～50m减小到-3m到3m,北向误差由-50m～50m减小到-5m～5m,并且随着历元时刻的增加,误差范围逐渐减小。说明EKF算法的滤波定位精度较高,方差较小,这为后续的整周模糊度解算提供较为精确的初始值。因为后续的整周模糊度解算要求伪距初始定位的误差方差在3m～5m以内,由下表可以说明EKF滤波定位已经可以达到为后续提供初始坐标的目的。

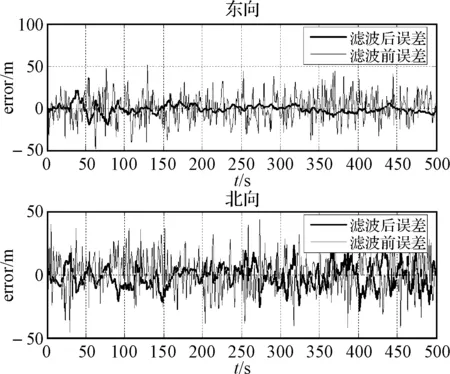
图4 模拟北斗数据下EKF滤波定位算法仿真

5 结语

本文通过采用扩展卡尔曼滤波的方法进行了模糊度参数估计,通过仿真数据进行了验证。扩展卡尔曼滤波法通过线性化观测方程的方法提高了模糊度参数估计的精度,并且在历元时刻较长之后可以减小观测误差,有利于后续的模糊度解算。

[1] 刘立龙,刘基余,李光成,等.单频GPS整周模糊度动态快速求解的研究[J].武汉大学学报:信息科学版,2005,30(10):885-887.

[2] 周巍.北斗卫星导航系统精密定位理论方法研究与实现[D].北京:解放军信息工程大学,2013(6).

[3] 邱蕾,花向红,蔡华,等.GPS短基线整周模糊度的直接解法[J].武汉大学学报:信息科学版,2009(1):97-99.

[4] 孙红星,付建红,袁修孝,等.基于多历元递推最小二乘卡尔曼滤波方法的模糊度解算[J].武汉大学学报:信息科学版,2008(7):35-39.

[5] 吴万清,宁龙梅,朱才连,等.一种单频单历元整周模糊度的解算方法[J].武汉大学学报:信息科学版,2005,30(6):497-501.

[6] 周忠谟,易杰军.GPS卫星测量原理与应用[M].北京:测绘出版社,1997:80,97-101.

[7] 刘基余.GPS卫星导航定位原理与方法[M].北京:科学出版社,2003:46-50.

[8] 刘超,王坚,路鑫,等.GPS载波相位观测值随机模型的比较研究[J].测绘科学,2010(6):151-154.

[9] 李保利.北斗多频高精度定位理论与方法研究[D].北京:解放军信息工程大学,2011,6.

[10] 邢喆,王泽民,伍岳.利用模糊度聚类方法筛选GPS载波相位组合观测值[J].武汉大学学报:信息科学版,2006(1):23-26.

[11] Teunissen, P. J. G. A New Method for Fast Carrier Phase Ambiguity Estimation[C]//Proceedings IEEE Position Location and Navigation Symposium PLANS94, Las Vegas, 11-15 April 1994:562-573.

[12] CHEN D. Fast ambiguity search filter(FASF): a novel concept for GPS ambiguity resolution[J]. Proceedings of GPS-93. Alexandria, Virginia: The Institute of Navigation,1993:781-787.

Fuzzy Degree Calculation Based on Recursive Least Square Kalman Filtering Method

XU Guannan WANG Jie

(Navigation Engineering, Naval University of Engineering, Wuhan 430033)

In view of the big dipper dynamic positioning regarding recursive least squares method as the basic, extended Kalman filter method is used to estimate the fuzzy degree of float solution. Thus using more epoch carrier phase observation information to solve the fuzzy degree of the whole week is achieved. Through test simulation by simulating beidou observation data, it proves that extended Kalman filtering method has high precision, and is suitable for dynamic positioning algorithm.

beidou dynamic positioning, least squares, extended Kalman, the whole week ambiguity

2014年10月8日,

2014年11月28日

徐冠楠,男,硕士研究生,研究方向:导航制导与定定位方向理论与应用。

TP301.6

10.3969/j.issn1672-9730.2015.04.011