基于CFD的低浓度水力碎浆机转子结构流场分析

王 侃 郭 楠

（北方工业大学机械与材料工程学院，北京100144）

0 引言

水力碎浆机是制浆造纸过程中用于碎解纸浆板和废纸等的传统机械设备。随着纸张品种和产量的增加，世界各国都加强了废纸的回收和再利用工作，废纸处理技术亦有了很大的发展，促进了水力碎浆机的不断改进和提高。水力碎浆机转子根据浆料的浓度可以分为高、低浓度两种结构，近些年来又发展出了中浓度转子。与低浓度碎浆机相比，中、高浓度水力碎浆机可以减少对纤维剪切的损伤，利于生产再生纸张，同时提高碎解效率、降低能耗，因此是废纸碎浆机的主要发展方向。但浆料在浓度大于10%时，流动性会变差，于是浆料不能充分循环，致使碎解效率低下，这就成为了高浓度水力碎浆机设计的难点。

CFD（Computational Fluid Dynamics），即计算流体动力学，以计算机为计算工具，运用各种离散化的数学方法以及数学模型，对流体动力学的各类问题进行数值实验、计算机模拟和分析研究，以解决各种实际问题。FLUENT软件的设计基于CFD软件群的思想，采用不同的离散格式和数值方法，以期在特定领域内使计算速度、稳定性和精度等方面实现最佳组合，从而高效率地解决各个领域的复杂流动计算问题［1］。

1 水力碎浆机转子结构模型的建立

1.1 几何建模

本文是根据已有低浓度转子来进行结构仿真模拟，在Solidworks中进行三维建模，具体结构如图1所示。将模型副本保存为.STEP文件格式，打开GAMBIT，执行File→Import→STEP，单击Browse选取之前保存的模型，选中stand－alone geometry中的3个选项以及heal geometry，GAMBIT会自动将Solidworks导进来的模型的多余线条去掉，自动予以完善。单击Accept将之前保存的.STEP格式文件导入GAMBIT软件中［1］。

图1 低浓度转子

在GAMBIT里进行网格划分之前，建立圆柱实体（Volume 2）代表碎浆机内液体。因所建立的液体模型与转子模型有部分重叠，故使用实体Subtract命令。用液体实体（Volume 2）剪去转子实体（Volume 1），且不保留剪切出的部分。

在GAMBIT里对几何体进行网格划分：因所建精准模型较为复杂，不便于划分网格，所划分出的网格数量较大且存在扭曲，会影响后续迭代计算的收敛性，故在不改变模型大致外观与仿真结果的条件下，对三维模型进行了简化处理。如图2所示，将传统低浓度转子的8个外伸叶片简化为6个，去掉叶片下与筛板的缝隙。

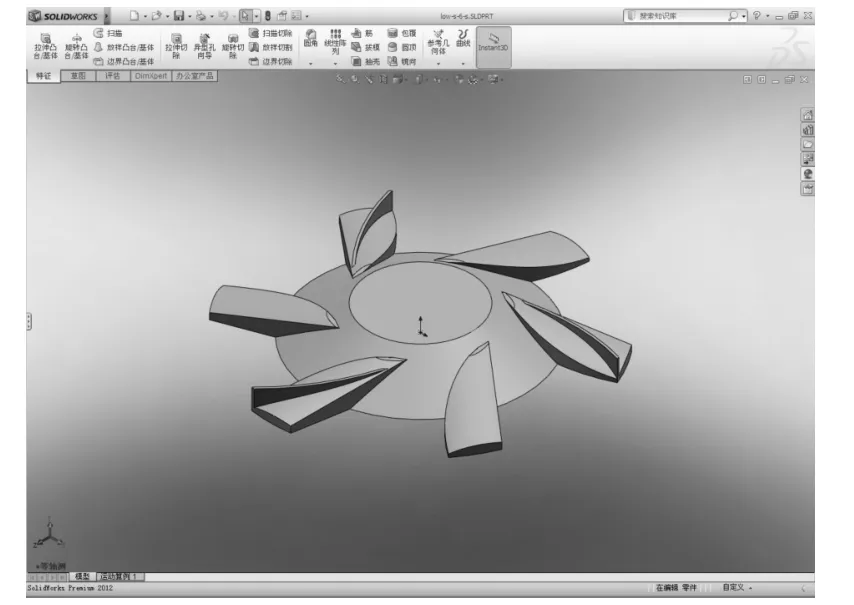
图2 低浓度转子（简化）

定义边界条件：液体的上下液面与外壁、转子壁面均定义为WALL，其中，转子壁面又分为转子结构的壁面与流体部分随转子结构的壁面。

定义介质类型：转子实体定义为SOLID，液体实体定义为FUILD。

在GAMBIT中完成必要的网格划分与边界、介质定义后，运用FLUENT进行流场模拟与迭代计算。将划分好网格的模型副本保存为.msh文件格式，以便后续对网格进行更改以及完善。另外，保存模型副本为.cas文件，以便后续导入FLUENT软件中。

1.2 数学模型

了解所要模拟流场特性是模拟流场的必要条件，这样才能选择正确的数学模型，并保证合理施加边界条件。碎浆机内部属于典型的湍流模型，流场由各种不同尺度的湍流涡叠合而成［2］，故选择标准的k－ε模型。下面介绍在直角坐标形式的绝对参照系下，描述其瞬时流动状态的基本控制方程［3］。

连续方程：

Navier－Stokes方程（动量方程）：

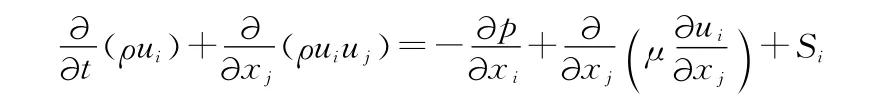
式中，ρ为流体的密度；u为速度；p为压力；t为时间；x为空间坐标；μ为动力黏度；S为源项；指标i、j表示坐标轴方向分量，遵从张量中的求和约定。

其湍动能方程（简称为k方程）表达式为如下形式［4］：

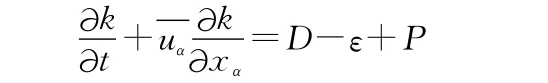
其中，D、ε与P分别称为扩散项、耗散项与生成项，其表达式分别为：

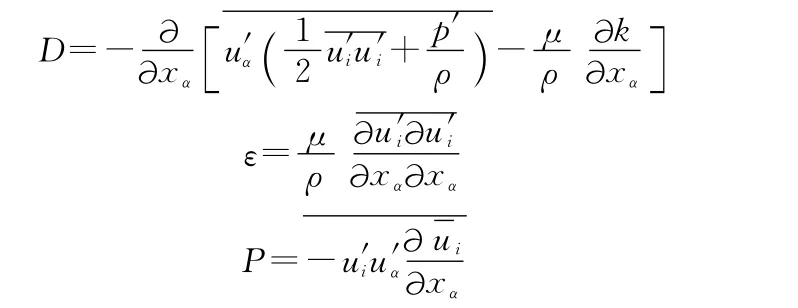
定义液体上、下及外壁为“Moving Wall／Relative to Adjacent Cell Zone／Rotational”。转子实体为“Moving Mesh”，给定转速1 000r／s。液体部分为“Moving Reference Frame”，给定相对转速10r／s。

定义收敛精度为0.01，给定时间步长为0.1s，非稳态计算。初始化后进行迭代计算。

2 模型的模拟仿真结果与分析

大约经过20 000步迭代，计算结果趋于收敛，各物理量趋于稳定，不再随迭代次数的增加而变化。CFD软件的优点之一便是强大的后处理功能，方便直接查看所需的相关数据。

对于不同浓度转子的流场模拟，静压是最能够直接影响转子使用寿命的数据，故主要分析压力，如图3所示。

图3 低浓度转子仿真结果

为方便观察比较仿真结果，取2个纵截面（X＝0，Z＝0）、3个横截面（Y＝0，Y＝5，Y＝9）来查看，如图4～8所示。

由图可知，同一水平面上压力场的分布规律基本上是随着半径的增大而增大的，从纵向上看，多个不同水平横截面的压力图基本一致，说明压力场在纵向上基本没有变化。

根据文献［5］，理想的自由涡流运动关系式为：

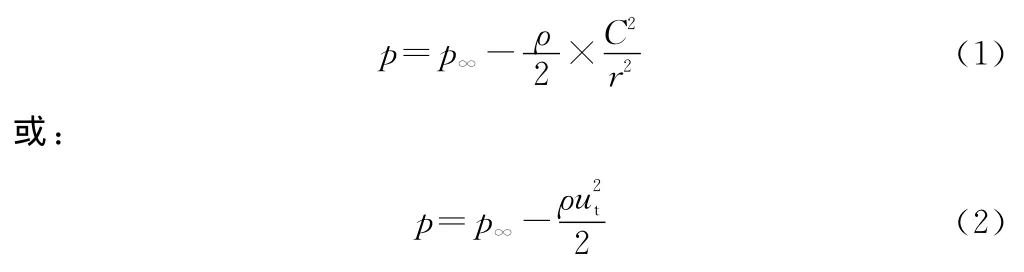
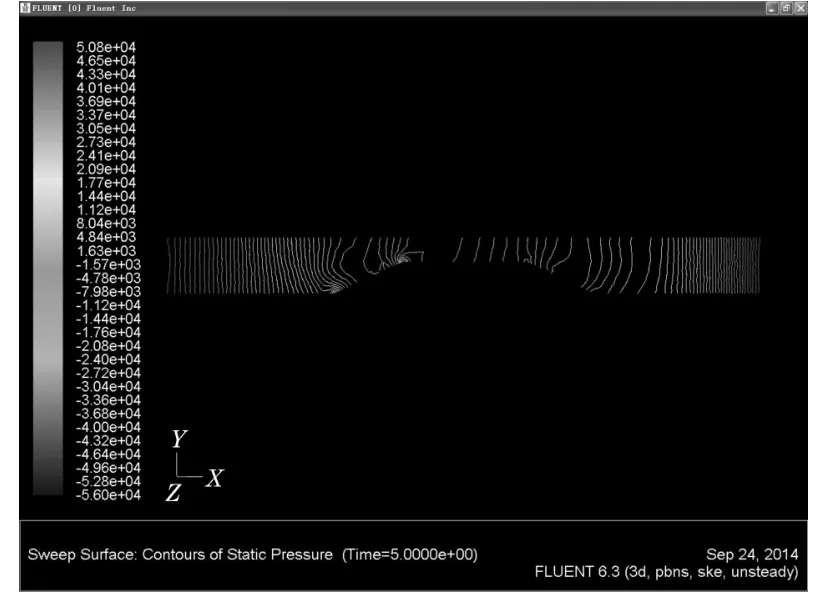
图5 Z=0

图6 Y=0

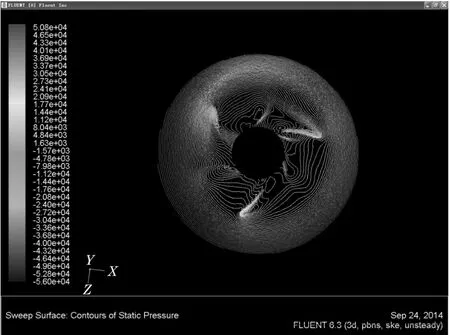
图7 Y=5

（1）、（2）两式相减得：

式中，p为半径r处压力；p∞为半径无穷大处压力；ρ为流体黏度；C为常数；ut为流体在半径r处的切向速度。

从验证关系式可知，切向速度是验证模拟仿真结果真实有效性的一个必要条件。根据图9切向速度沿截面（截面Y＝0）半径的分布曲线，取各半径处的切向速度均值，代入上述公式（3），验证模拟仿真结果的收敛性。

图8 Y=9

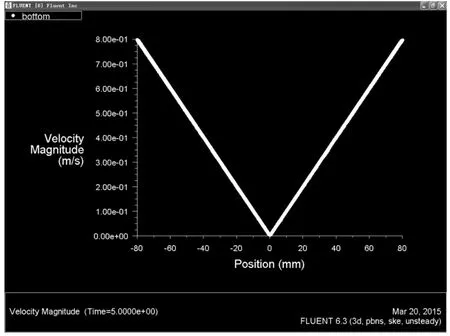
图9 切向速度沿截面半径的分布曲线

3 结语

以上模拟仿真结果代入文献［5］所提供的验证公式后，数值吻合，证明了模拟仿真结果的可靠性，为下一步的结构设计与计算提供了有效的数据支持。通过分析主要参数的模拟数据结果，发现碎浆机内部运动基本符合自由涡运动规律，为碎浆机转子结构的设计提供了可靠依据。

［1］周俊波，刘洋，等.FLUENT6.3流场分析从入门到精通［M］.北京：机械工业出版社，2012

［2］王福军.CFD在水力机械湍流分析与性能预测中的应用［J］.中国农业大学学报，2005，10（4）：75～80

［3］Ohashi H.Vibration and Oscillation of Hydraulic Machinery［M］.Cambridge University Press，1991

［4］王保国，蒋洪德，马晖扬，等.工程流体力学（上册）［M］.北京：科学出版社，2011

［5］任连城，梁政，钟功祥，等.基于CFD的水力旋流器流场模拟研究［D］.西南石油学院，2005