多锤电驱式激振系统的振动耦合特性及控制*

廖高华 来鑫 乌建中†

（1.同济大学机械与能源工程学院，上海 201804；2.上海理工大学机械工程学院，上海 200093）

多锤电驱式激振系统的振动耦合特性及控制*

廖高华1来鑫2乌建中1†

（1.同济大学机械与能源工程学院，上海 201804；2.上海理工大学机械工程学院，上海 200093）

针对振动锤联动激振耦合特性，以两振动锤为对象建立动力学模型，利用拉格朗日方法推导系统数学方程；基于能量分布法对耦合过程中的能量分布进行求解，分析了激振系统在各频率段的耦合规律，利用哈密顿原理推导系统振动同步的条件，得到相位差所处的稳定区间；构建多锤激振的同步控制系统，对耦合作用下的同步控制进行研究，确立了相邻偏差耦合转速调节及虚拟锤点动相位调节控制方式，并进行理论分析和控制方式的试验验证.结果表明：共振点的外耦合能量对相位差不产生影响，相位差有在低频区朝零趋近、近共振区朝±/2趋近及超共振区朝±趋近的趋势；采用相邻偏差耦合转速调节及虚拟锤点动相位调节控制方式，系统同步效果良好.

多锤激振；耦合特性；控制策略；自同步

振动锤联动技术解决了单个振动锤对大直径桩基施工时功率不足的问题.目前工程上振动沉桩机普遍使用同步齿轮来同步，存在机械结构与安装复杂、齿轮等传力部件易于损坏等问题［1-2］.振动锤设计中没考虑系统自身特性对同步性影响，这使得同步齿轮在打桩过程中受到较严重的摩擦和冲击，从而导致齿轮传动系统发热大、温升高、齿轮频繁损坏，大大缩短了振动锤的使用寿命.针对这些问题，荷兰PVE公司提出了一种电控联动方法，电测相位差，并利用计算机软件实时修正相位差［3-4］；文献［5-6］对液压振动桩锤的沉桩动力学及调频调矩控制、同步特性及控制等进行了详细研究.研究发现，桩锤联动激振系统在工作中存在较强的耦合作用，与其他振动同步机械系统的耦合特性［7-10］不同，振动桩锤间的耦合作用受土壤参数、振动锤安装位置等因素的影响.

振动桩锤间存在较强的机电耦合影响控制同步效果［11］，通过智能控制方式使得机构在工作过程中达到同步效果将成为一个新的发展趋势.研究锤联动耦合振动特性及控制，对多锤联动激振技术的发展具有重要意义.文中针对两电驱式锤联动激振系统，建立联动系统动力学模型，并利用能量分布法对激振系统在各频率段耦合规律进行分析，通过对耦合过程中能量分布求解，揭示耦合特性与机理，研究了耦合作用下的同步条件及控制策略，并通过试验对理论推导结果的正确性进行验证.

1 振动系统的机电耦合数学模型

在沉桩过程中，土壤刚度相比桩要小得多，根据巴尔坎的振动打桩理论及文献［11-12］，作如下合理假设：土壤为弹性体，振动锤与桩为均质刚体，土壤对桩的弹性力和阻尼力分别是桩位移与运动速度的线性函数.振动系统力学模型如图1所示，图中Oxyz为绝对坐标，O′x′y′z′为动坐标，φ为坐标系间夹角，o″为振动机体质心，o′为运动合成质心，oi为振动锤偏心块旋转中心连线中点，li=ooi，l0=oo′，βi=∠oiox（i=1，2），θi（i=1，2）为偏心块的旋转角度.

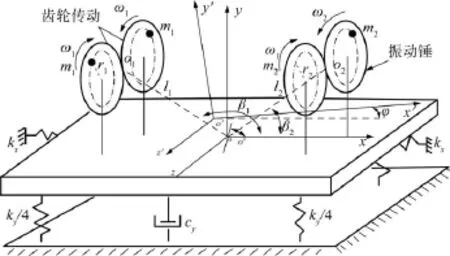
图1 两振动锤振动系统模型Fig.1 Two vibration hammer excitation system model

选取x、y、φ、θ1和θ2为广义坐标，根据拉格朗日方程，得到振动系统的动力学方程为

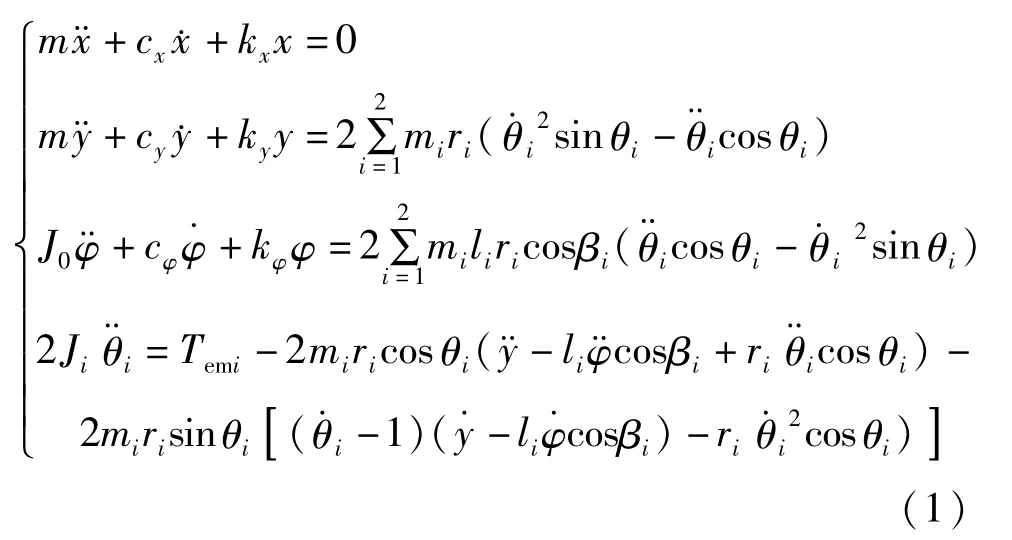
式中：i=1，2；kx、ky、kφ为土壤刚度系数；cx、cy、cφ为土壤阻尼系数；J0为振动系统转动惯量；Ji为电机i的转动惯量；m为振动锤和桩的总质量；mi为偏心块i的质量；ωi=为两振动锤偏心块旋转角速度；ri为偏心块的偏心距；Temi为电机i转轴上的电磁转矩.

振动桩锤电机采用二相同步旋转坐标系下的数学模型，其状态方程［13］与式（1）动力学方程构成了两锤激振系统机电耦合数学模型.从模型上看是振动系统与动力系统相互影响的非理想系统，它表达了在系统振动过程中两者之间的耦合关系.

2 全频率区域耦合特性分析

基于能量分布法对激振系统在各频率段的耦合规律进行分析，通过对耦合过程中能量分布求解，定性地分析3种频段区的机电耦合规律.当两台振动锤同时进行激振时，系统激振力叠加，激振对象受到的合力为F，振动系统的振动速度为vy=.根据功率流方法（即功率流的大小等于力与速度的点积），假定两振动锤的机械结构、几何尺寸、电机性能等参数一致以及振动锤对称布置，当振动锤的偏心块的旋转频率等于系统的振动频率时，两振动锤输出功率分别为

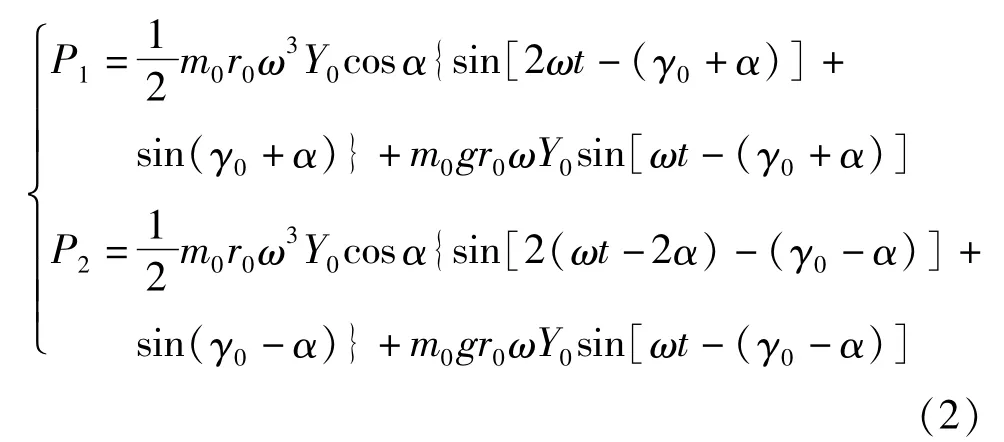
电机输出功率由3部分构成：振动锤自身旋转产生的能量波动，定义为内能量耦合Pini（ω，t）；与相位相关的固定值，可看成振动锤之间的耦合能量传递，定义为外能量耦合Pouti（α，t）；偏心块旋转时的势能.机电耦合作用是3部分共同作用的结果，内耦合能量及外耦合能量定义如下：

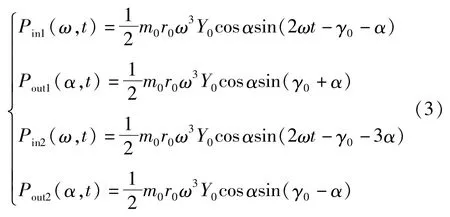
由式（3）得到内耦合引起的能量分布差可为

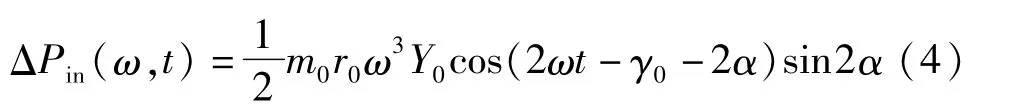
式（4）用图形表示如图2所示，内耦合引起的能量差与振动响应状态、相位差密切相关.在处于超共振区时（γ0≈），当相位差2α=±或0时，两振动锤耦合功率差ΔPin=0，相位差越靠近0或±，ΔPin波动越小；当相位差2α=±/2时，ΔPin波动最大，相位差越靠近±/2，ΔPin波动越大.

由于式（4）为时变周期函数，因此求取一个周期内ΔPin平均值，通过平均值的变化规律近似等效内耦合变化情况，可表示为

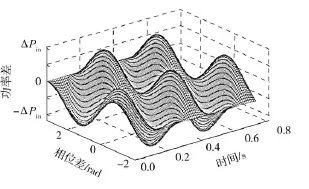
图2 超共振下内耦合功率分布Fig.2 Inner coupling power distribution in super resonance

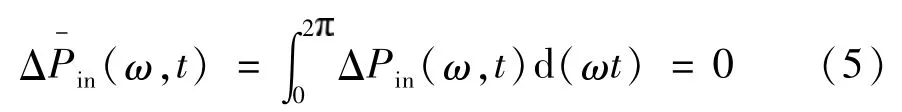
由式（5）可知，内耦合能量在一个振动周期内的平均值为零，因此在分析机电耦合时可近似认为相位差的改变是外耦合引起.

由式（3）可得外耦合能量差，表示为

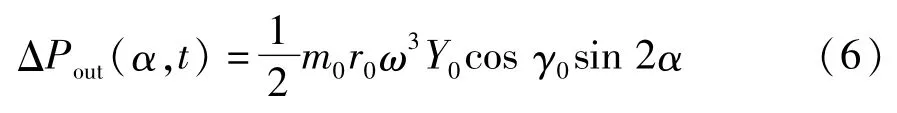
据式（6）可得外耦合引起的两电机功率分布，如图3所示.

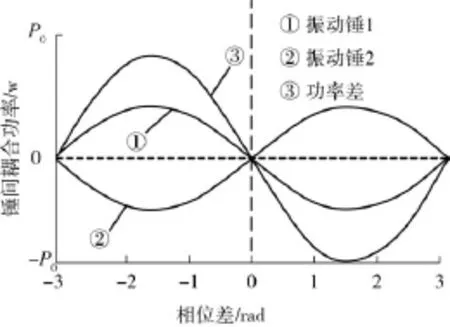
图3 振动锤外耦合功率分布Fig.3 Power distribution of vibratory hammer out coupling

由图3可见，两电机轴系上产生的功率分布不一致，从而使相位差变化达到功率的自动平衡状态，相位差会朝区间（-，）内的某值趋近，整体趋势为外耦合作用使相位差有向零度或附近逼近的趋势，外耦合引起的能量差还与振动响应参数γ0相关.

（1）超共振区机电耦合特性分析

系统在超共振区时（γ0≈），由式（6）可得外耦合能量差关系：

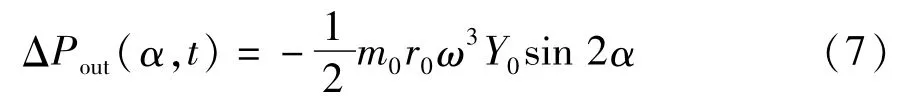
由式（7）可知，在超共振情况下，当相位差2α∊（0，）时，ΔPout＜0，为了使能量平衡，相位领先的振动锤加大能量输出，相位差朝趋近；当2α∊（-，0）时，相位领先的振动锤的输出功率大于相位落后的振动锤，相位差朝-趋近.据以上分析可知，在超共振情况下，为了保持两电机的能量输出平衡，相位差有朝±趋近的趋势.

（2）低频区机电耦合特性分析

系统在超共振区时（γ0≈0），由式（6）可得外耦合能量差关系：

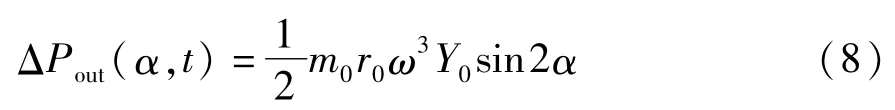
此时外耦合达到最大值，当相位差2α＞0时，ΔPout＞0，相位差有朝零度趋近的趋势；当相位差为零时外耦合能量达到平衡.据以上分析可知，当处于低频区时相位差有朝零度趋近的趋势.

（3）共振区机电耦合特性分析

当处于共振条件时（γ0≈/2），代入式（3）得外耦合能量表达式：

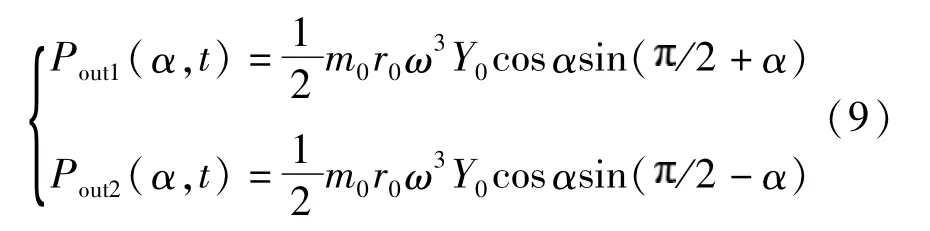
稳定状态时两电机的能量分布均匀，即Pout1= Pout2.由式（9）可知，不论相位差为何值，两振动锤外耦合能量都相等，即在共振点，外耦合对相位差的分布没有影响.综合上述低频区及超共振区的特性，可得出在共振点及近共振区的机电耦合特征：相位差有朝±/2趋近的趋势.

3 振动系统的同步条件

运用哈密顿原理求解两振动锤系统实现振动同步的条件，根据图1的两桩锤振动系统力学模型，在广义坐标x、y、φ、θ1和θ2下，系统的动能Ek、势能En代入哈密顿数学表达式得哈密顿作用量（表示一个动力物理系统内在的演化趋向）H为

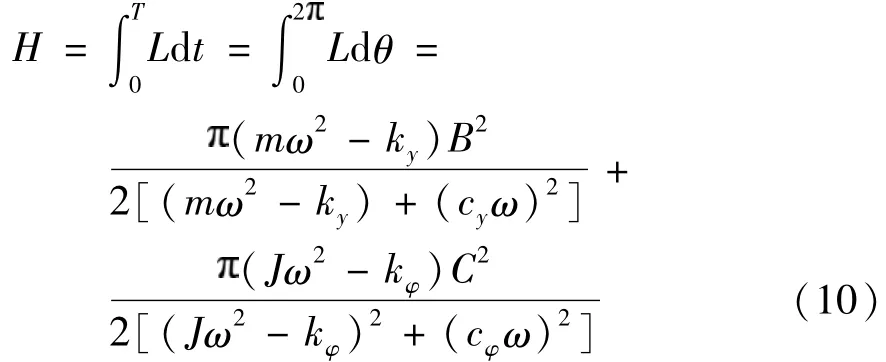
取α为广义坐标，采用虚功方法求振动系统的广义力表达式为

由|sin2α|≤1及式（11）可知，两振动锤激振系统振动同步的必要条件为

可见，要达到较好自同步效果，电机参数需相近.振动锤的偏心力矩越大，越容易进入自同步状态.当偏心块之间的转速相近时，由于负载转矩的重新分配，两电机的转速与相位差会自动趋于一致.同步性转矩Tt越大，系统越容易进入同步状态，偏转振动对于同步是有益的.

根据哈密顿原理和数学极值方法，系统稳定的条件是哈密顿作用量存在极值，对其化简可得：

式（13）为两锤激振系统的同步稳定性条件，定义S为振动系统稳定性参数.当振动体在超共振情况下，参数S＞0时，即振动机体偏转运动对振动机体的影响大于y方向上，相位差2α的稳定区间为［-/2，/2］，反之稳定区间为［/2，3/2］.

4 耦合同步控制策略

控制同步通过调节转速消除相位差，当电机转速差大于设定值时，启动转速调节器减小转速差，否则启动相位调节控制器消除相位差［14］.

（1）相邻偏差耦合转速调节器

各振动锤转速初值以同一个基准转速为参考，考虑振动锤自身转速差反馈，同时还考虑与之相邻的一台振动锤的转速，将相邻转速偏差引入到当前振动锤转速控制中，形成环形网络控制系统.用同步及跟随误差描述系统同步性能，控制算法使同步误差εi（t）及跟随误差ei（t）都趋于零，转速控制策略如图4所示.

（2）虚拟锤点动控制的相位调节器

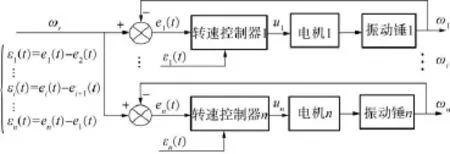
图4 电机转速控制策略Fig.4 Motor speed control strategy

采用独立硬件及程序产生与真实传感信号一致的虚拟相位信号作为基准，相位调节控制目的就是消除各振动锤相位信号与基准信号的相位差.考虑耦合作用对电机的转矩存在驱动与阻碍作用及给控制带来的其他影响，采用点动BangBang算法［15］.它的基本原理是：当速度差小于设定的速度阈值VT时进入相位调节控制器，振动锤偏心块旋转一圈，进行一次相位调节，设此时第i台（i≥1）从振动桩锤的控制量为ui，检测振动锤偏心块与虚拟振动锤之间的相位差，由下列算法得出当前的控制量Ui（t）：

式中，λj为点动控制系数，Δu（t）为控制增量.Δu（t）可用下式表示：

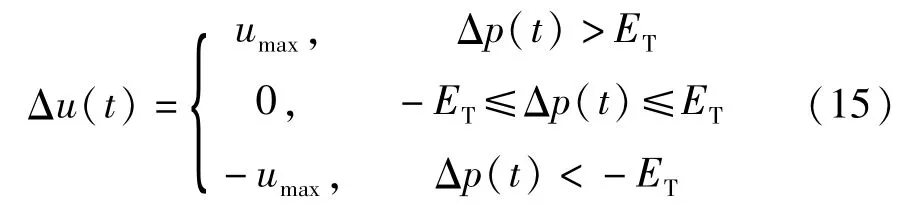
式中，Δp（t）为实时检测的相位差，ET为设定相位差的阈值，umax为设定控制量.

基于控制方式对耦合模型进行同步数值仿真分析，如图5所示.从图可看出“虚拟点动控制”方式可较好地实现相位的同步控制，在工程中易于实现.

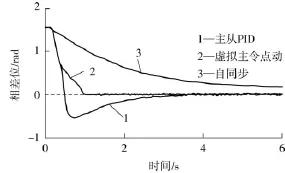
图5 机电耦合相位控制同步Fig.5 Electromechanical coupling phase control synchronous

5 试验研究

两振动锤系统进行沉桩试验，验证耦合特性及控制效果.系统中桩长9.8m，直径1.45m，质量7.7 t，采用ABB的ACS550变频器、MEMS器件ADIS16209进行驱动控制及振动加速度测量.变频器控制电机转速，传感器检测偏心块位置，控制器记录并分析计算转速及相位差等参数，试验装置如图6所示.

图6 现场试验装置Fig.6 Field test device

图7为耦合控制试验转速与相位同步曲线，其中n1、n2分别表示振动锤1、振动锤2的转速，由图7（a）可看出，两振动锤的转速同步情况较好，两振动锤在控制作用下相位差趋于同步，说明控制策略与算法的有效性.图7（b）为桩下沉3m时自同步曲线与控制同步的相位差试验结果.当两振动锤电机转速差较大（30 r/min）时，系统不能进入自同步状态；当电机转速差较小时，相位差会稳定在固定角度且有小波动，通过控制方法能够消除由机电耦合带来的固定相位差，促使相位差稳定地维持在零度附近，实现两振动锤的激振力最大合成沉桩.

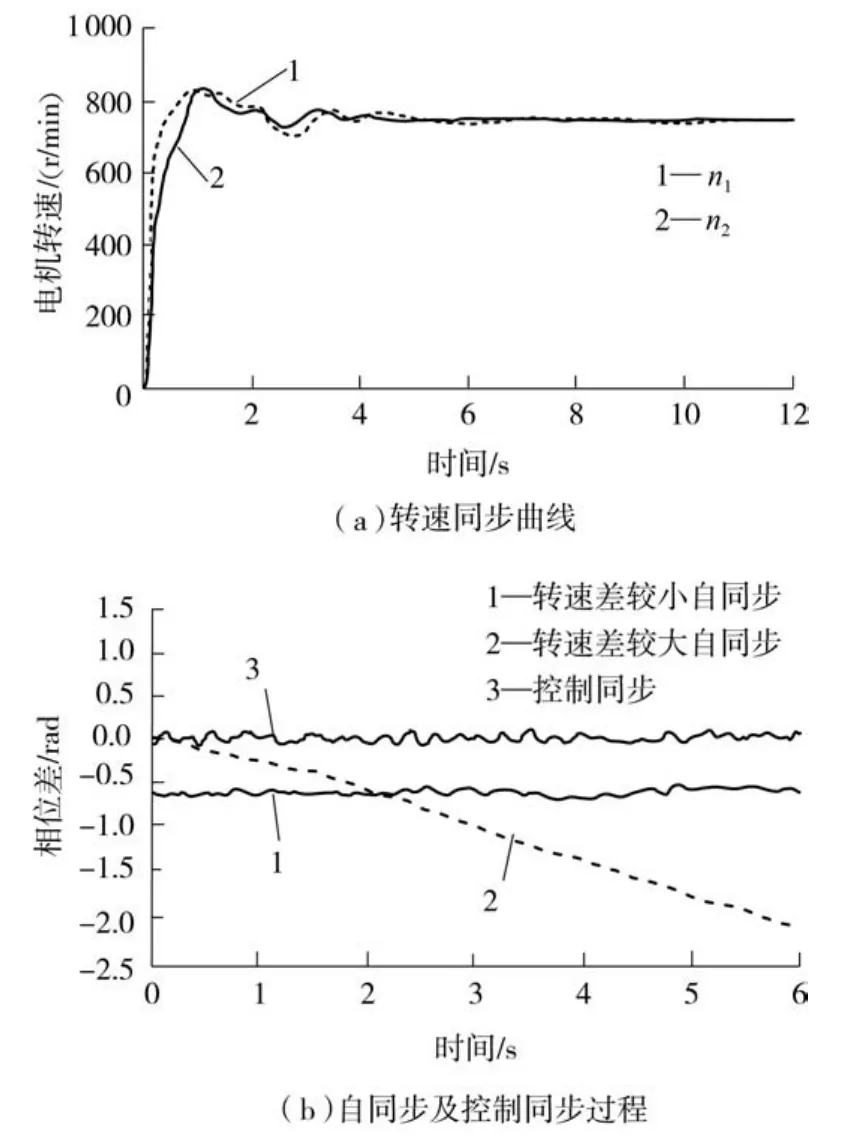
图7 耦合控制特性试验曲线Fig.7 Test curves of coupling control characteristics

沉桩过程中，当振幅百分比达到60%时发生了频率与相位的跳变现象，控制同步曲线如图8所示.

图8 振幅百分比为60%时的同步控制曲线Fig.8 Synchronous control curves of60%amplitude

通过控制方法使相位差减小，系统的振动加速度加大，电机所受的负载转矩加大，因此相位差超前的电机首先发生频率跳变，相位差迅速增大，两电机的负载变小，转速迅速增大后恢复正常，后控制手段减小相位差，如此反复，两电机的转速交替朝相反的方向突变，相位差超前的振动锤首先发生突变.试验表明同步控制在电机功率不足时是无能为力的，设计振动系统时应该考虑最大加速度（在相位差等于零时）选择合适功率的电机.

6 结论

（1）多锤激振系统中存在较强的耦合作用，振动锤间有较强的力与能量传递，使各电机的外负载转矩变化，在一定条件下耦合出现相位差自动趋于某个值.共振点的外耦合能量对相位差不产生影响，相位差有在低频区朝零趋近、近共振区朝±/2趋近及超共振区朝±趋近的趋势.

（2）系统采用控制同步方式改变转速消除相位差，耦合作用在多数情况下阻碍控制同步.考虑机电耦合及电机功率对控制影响，设计了相邻偏差耦合转速调节器及虚拟点动控制相位调节器，仿真分析与实验均表明，系统同步效果良好.

（3）试验验证了同步控制必须在电机功率匹配基础上进行，电机额定功率越大，振动系统对动力驱动系统的扰动越小，耦合作用对电机转速的影响越小，控制效果越好.电机机械特性越硬，对控制同步是有利的，当相位同步要求较高时可考虑使用同步电机.

［1］ Mahboob I，Nier V，Nishiguchi K，et al.Multi-mode parametric coupling in an electromechanical resonator［J］. Applied Physics Letters，2013，103（15）：1-4.

［2］ Khoubani Ali，Ahmadi，Mohammad Mehdi.Numerical study of ground vibration due to impact pile driving［J］. Proceedings of the Institution of Civil Engineers Geotechnical Engineering，2014，167（1）：28-39.

［3］ 范期锦.多台大型液压振动锤联动工作的同步性问题［J］.中国港湾建设，2003（2）：1-4. Fan Qi-jin.Synchronization of large hydraulic vibrators when working together［J］.China Har Bour Engineering，2003（2）：1-4.

［4］ Hall M V.A semi-analytical model for non-mach peak pressure of underwater acoustic puleses from offshore pile driving［J］.Acoustics Australia，2013，41（1）：42-51.

［5］ 刘指先.四轴液压振动桩锤的同步特性及其控制研究［D］.长沙：中南大学机电工程学院，2011.

［6］ 罗春雷.液压振动桩锤沉桩动力学及调频调矩控制研究［D］.长沙：中南大学机电工程学院，2005.

［7］ 闻邦椿，赵春雨，苏东海，等.机械系统的振动同步与控制同步［M］.北京：科学出版社，2003.

［8］ Zhao Chun-yu，Zhu Hong-tao，Wang Rui-zi，et al.Synchronization of two non-identical coupled exciters in a non-resonant vibrating system of linearmotion［J］.Shock and Vibration，2009，16（5）：505-515.

［9］ 魏巍，杨志东，韩俊伟.基于动力学耦合模型的超冗余振动台解耦控制［J］.华南理工大学学报：自然科学版，2014，42（4）：124-130. WeiWei，Yang Zhi-dong，Han Jun-wei.Decoupling controlof hyper-redundant shaking table based on dynamic coupling model［J］.Journal of South China University of Technology：Natural Science Edition，2014，42（4）：124-130.

［10］ Guo Y，Hu J，Zhang L Y.Finite element analysis of multi-body contacts for pile driving using a hydraulic pile hammer［J］.Proceedings of the Institution of Mechanical Engineers Part C：Journal of Mechanical Engineering Science，2011，225（5）：1153-1161.

［11］ Blekhman i I.Synchronization in science and technology［M］.New York：ASME Press，1988.

［12］ 朱合华，谢永健，王怀忠.打桩锤击解析模型及垫层材料参数的优化［J］.同济大学学报：自然科学版，2004，32（7）：841-845. Zhu He-hua，Xie Yong-jian，Wang Huai-zhong.Analytical solution for pile hammer impact and application of optimum design technique for determining cushion parameters［J］.Journal of Tongji University：Natural Science Edition，2004，32（7）：841-845.

［13］ 王锋，姜建国，颜天佑.基于Matlab的异步电动机建模方法的研究［J］.系统仿真学报，2006，18（7）：1733-1741. Wang Feng，Jiang Jian-guo，Yan Tian-you.Methods of asynchronousmotor model simulation based on Matlab［J］.Journal of System Simulation，2006，18（7）：1733-1741.

［14］ 来鑫，乌建中，周文，等.桩锤同步振动系统的机电耦合特性及同步控制［J］.同济大学学报：自然科学版，2012，40（6）：920-925. Lai Xin，Wu Jian-zhong，Zhou Wen，et al.Synchronization control and electromechanical coupling characteristics of pile hammer synchronous vibration system［J］. Journal of Tongji University：Natural Science Edition，2012，40（6）：920-925.

［15］ 刘豹，唐万生.现代控制理论［M］.北京：机械工业出版社，2006.

Coupling Characteristics of Electrically-Driven M ulti-Hammer Excitation System and Its Control

Liao Gao-hua1Lai Xin2Wu Jian-zhong1
（1.School of Mechanical Engineering，Tongji University，Shanghai201804，China；2.School of Mechanical Engineering，University of Shanghai for Science and Technology，Shanghai200093，China）

In order to solve the coupling problem ofmulti-hammer excitation，firstly，a dynamicmodel of two vibration hammers is constructed and amathematical equation of system is deduced bymeans of the Lagrangianmethod. Next，the energy distribution during the electromechanical coupling process is solved through the energy distribution method，the coupling laws of the excitation system in each frequency range are discussed，and the conditions of system vibration synchronization are deduced on the basis of the Hamilton principle.Thus，the stable region of phase difference is obtained.Then，a synchronous control system formulti-Hammer excitation is established to investigate the synchronous controlwith coupling，and a controlmode on the basis of the speed regulation of adjacent deviation coupling and the dynamic phase regulation of virtualmaster bang-bang is proposed.Finally，both the theoretical analysis and the proposed controlmode are verified by tests.The results show that（1）the coupling energy of resonance points do notaffect the phase difference；（2）the phase difference tends to be zero in a low frequency range，±/2 in the region close to resonance and±in the super-harmonic resonance region；and（3）the proposed controlmode achieves a good system synchronization effect.

multi-hammer excitation；coupling characteristic；control strategy；self-synchronization

TH113

10.3969/j.issn.1000-565X.2015.07.018

1000-565X（2015）07-0130-06

2014-12-02

上海市产学研合作计划项目（20131628）

Foundation item：Supported by the Shanghai Industry-Academia-Research Cooperation（20131628）

廖高华（1978-），男，博士生，主要从事机电液控制研究.E-mail：86655319@qq.com

†通信作者：乌建中（1953-），男，博士，教授，主要从事机电液控制研究.E-mail：tjjd328@163.com