川中丘陵地区土地利用空间分布的分形分析

段含明，张雪梅

(西华师范大学国土资源学院，四川 南充 637009)



川中丘陵地区土地利用空间分布的分形分析

段含明，张雪梅

(西华师范大学国土资源学院，四川 南充 637009)

以南充市搬罾镇和凤山乡为例，采用盒计数法提取了川中丘陵地区不同类型土地利用图斑的计盒维数；并分析分维值蕴涵的土地利用空间分布特征及其影响因素. 结果表明：川中丘陵地区村镇尺度上，主要土地类型的空间分布具有显著的分形特征. 不同土地类型的分维值介于1-2之间；其中以坑塘为主的水利设施分维值趋于1；面积大、连片分布的耕地趋于2. 计盒维数能指示土地类型在行政区内的占据度和在外接正方形空间中的填充度，分维值越大，占据度和填充度越大. 在村镇尺度上，土地利用的分维值与地形、农户户数未检测出明显的相关性.

分形；计盒维数；土地利用；空间分布；川中丘陵

土地利用是人类活动与自然环境双重作用的产物，综合反映了人类活动、社会经济以及自然环境之间的相互作用，是区域和全球环境变化的指示器. 由于多重环境因子的共同作用，土地利用的空间结构具有破碎、不规则和复杂性等特点，以至于传统的欧氏几何难以有效刻画，须借助分形几何学来探寻其内在的规律和特点.

分形几何学由美籍数学家Mandelbrot于19世纪60-70年代创立. 分形指那些表面上看似杂乱无章、支离破碎，但其组成部分以某种方式与其整体存在相似的几何形状. 分形几何学被广泛应用于土地利用/覆被和景观的空间格局研究，以揭示在表面的杂乱无章背后暗含的空间分布格局的内在规律. 应用的关键在于分维值的提取及其地理含义的解释. 常见的分维值提取方法包括周长-面积法和盒计数法，二者得到的分维值及其内涵并不完全一致[1, 2]. 周长-面积法提取的结果是反映土地斑块边界特征的形状维数[3-6]，该算法涉及图斑周长值，受矢量数据编辑的精细程度影响显著，具有主观性和随机性；同时，土地分形是统计分形，对统计样本即同一类型土地图斑数量有要求，数量过少将失去统计意义，这一点已被少量文献所注意到[7]. 统计样本量过小的情形在小区域尺度的研究中会比较明显. 盒计数法用于提取计盒维数，主要表征图斑的几何形状和地类对空间的占据程度. 从计算方法看，图斑边界编辑的精细程度对分维值影响不明显；统计分维值的可靠性主要与格网细化的等级数量相关，而与图斑数量无关，有效避免了小区域尺度上图斑数量过少的问题. 因其构造简单、容易计算，盒计数法被广泛应用于地理研究的各个领域[1, 8-11]；采用盒计数法和计盒维数分析土地利用空间分布特征，便于同其他地理要素的研究进行比较.

川中丘陵地区人口密集、土地利用区域特征独特；在村镇尺度上研究土地利用的分形特征及其影响因素，归因更加明确. 已有部分学者作了相关尝试[12, 13]，但总体上研究并不充分. 本文拟采用盒计数法，在村镇尺度上提取川中丘陵地区典型样区不同土地利用类型的计盒维数，讨论其对土地利用空间分布特征的指示性；并将地形数据、农户户数与分维值进行关联，探索计盒维数在丘陵地区的影响因素.

1 研究区概况

研究样区位于四川省南充市顺庆区搬罾镇和凤山乡，106°07′-106°13′E，30°53′-31°00′N之间，属南充市区西北远郊，分别距离市区约16km和24km；居嘉陵江西侧，为川中丘陵腹心地带，低丘地貌，丘坡多辟为梯地梯田；中亚热带湿润气候，年降雨量约1 100mm；耕地占区内土地的绝大部分，主要种植玉米、水稻、油菜和蔬菜.

其中搬罾镇辖12个村，选其中连片分布的石庙子、杨四坝、凉水井、小河坝4村为研究样区，共计11.53km2，有居民2 644户；区内最高处海拔453m，最低海拔250m. 凤山乡居搬罾东北，辖9个村，选择其中连片分布的黑塔沟、马家山、老鹰寺及蔡家沟4村为研究样区，共计8.01km2，有居民1 053户；区内最高处海拔479m，最低海拔290m. 8个村均不是乡镇政府(集镇)所在地.

2 研究方法

2.1 数据来源

主要涉及土地利用数据、数字高程模型(DEM)和农户户数数据. 土地利用数据经1∶1000正射航空影像全野外调查绘制，航拍时间为2013年5月. 全部土地归入耕地、林地、建设用地3大类，其中建设用地包含宅基地及其附属物、小型水利设施和宽度超过1m的道路. 为准确揭示土地利用的分形特征，提取建设用地的子类—宅基地和水利设施，与耕地、林地和作为大类的建设用地一起参与分形分析. 宅基地是以房屋屋檐滴水线为界包络的图斑；水利设施包括以灌溉为目的的坑塘、蓄水池、水库、水渠、机井及其配套设施等. 本文主要讨论农村集体所有权的土地，研究区内的自然河流水面及河滩地不考虑在内；其面积很小，不影响分析结果.

数字高程模型采用ASTER GDEM第1版数据，空间分辨率30m，研究样区内未见明显异常值. 分别用两乡镇8个村的边界矢量数据，对其进行裁减，并提取各村的地形特征值. 各村农户户数由政府相关部门提供.

2.2 计盒维数

计盒维数采用盒计数法计算，基本思路是：用边长不同的正方形格网将同一类别图斑全覆盖；因为图斑不规则、且可能中空，则必然有部分格子是空的；随着正方形边长d的变化，统计对应条件下非空格子数N(d)，从而形成一系列的d和对应的N(d)值；取二者的自然对数，形成lnd与lnN(d)；对它们进行回归分析. 如果他们满足以下线性关系，则拟合直线的斜率D(取绝对值)即为测量对象的分维值：

lnN(d)=-D·lnd+c (c为待定常数).

盒计数法的应用通常还做如下处理：为确保测量对象的全覆盖，最粗格网为测量图形的最小外接正方形，仅含一个格网；第二次覆盖时，正方形边长缩小一半，变成2×2格网；类似地，格网边长按照d、d/2、d/4……等比数列递减，直到足够小[8].

3 结果与分析

3.1 土地利用有无分形特征的判定

应用分形理论分析土地利用，前提是判定土地图斑是否具备分形特征. Benguigui等[8]以lnN(d)与lnd的线性拟合度R2是否大于0.996，作为适用于计盒维数的判定标准；但同时指出这是基于目视结果、具有随意性的经验标准. 由于土地图斑即便具备分形特征，也只是统计意义上的分形，故本文通过检测lnN(d)与lnd是否显著线性相关，来确定分形特征是否成立；显著性的检测采用相关系数检验法实现(表1). 结果表明，所有土地类型的相关系数(R)值，都大于对应条件下“十分显著”状态的相关系数最小值(Rmin). 故搬罾和凤山的耕地、林地、建设用地、以及宅基地和水利设施均具备分形特征，可以应用分形理论进行后续分析. 以下讨论基于计盒维数展开.

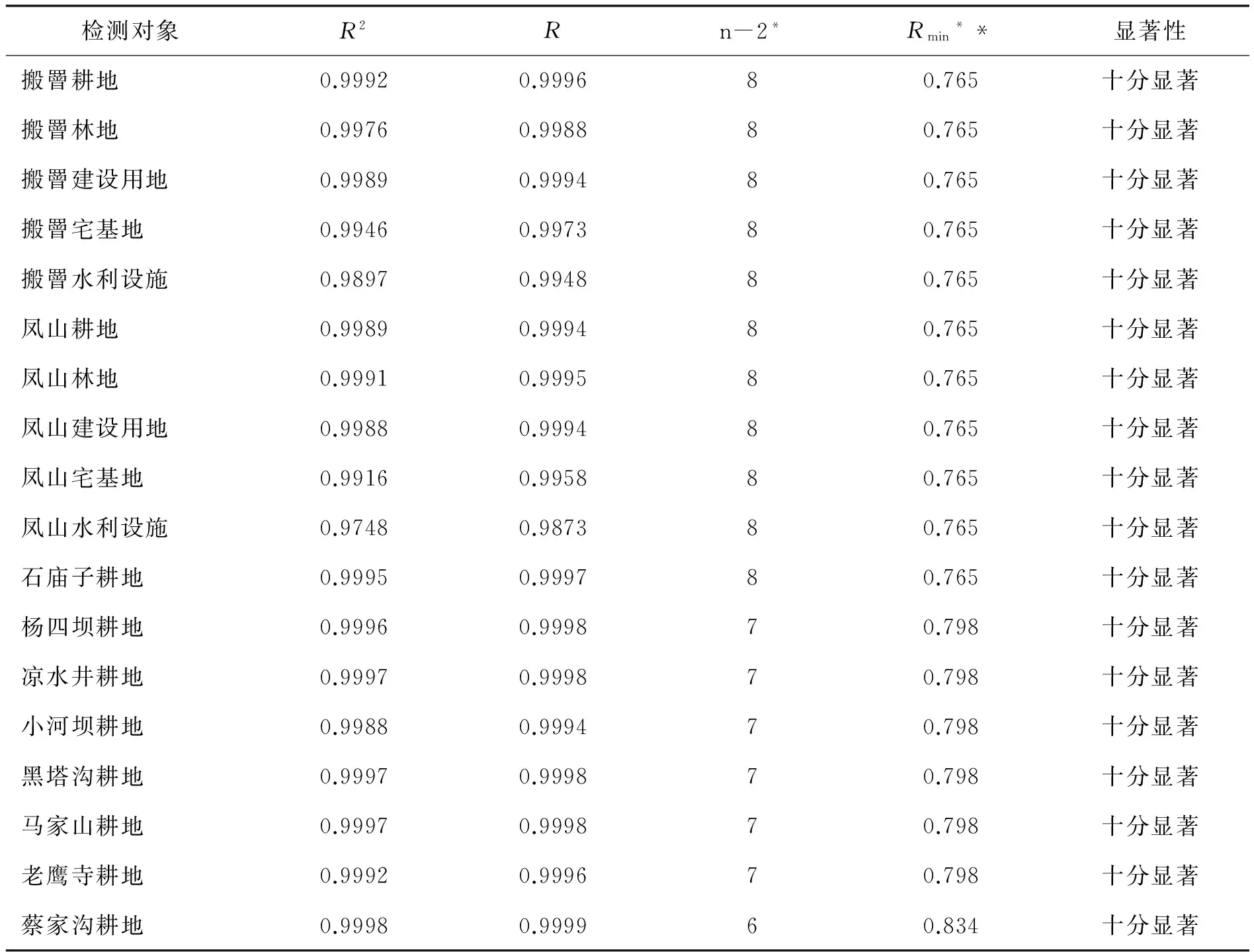
表1 不同土地利用lnd与lnN(d)线性相关的显著性检验

*n指盒计数法中边长不同的格网的种类数量；**Rmin指满足“十分显著”的线性相关时，在给定的n值下相关系数的最小值.

3.2 土地利用分维值的指示含义

3.2.1 土地利用分维值的图形含义

计盒维数一般介于0-2之间，取值趋于2则地物接近满铺的正方形分布，边界不规则和空洞的存在会降低分维值；呈点状分布的地物，取值趋于0. 表2-表5显示，耕地分维值较大，都超过1.7；这与耕地是本区域最主要的土地利用方式、几乎完全填充整个研究区的特征相符. 水利设施分维值较小，其中凤山取值1.0318. 凤山乡的水利设施由分散分布的坑塘、水池构成；因为工作比例尺较大，土地利用图上其并不表现为点，而是具有一定面积、相互分离的有限数量图斑，所以取值介于点和面之间. 其他类型的土地无论是单个图斑面积还是总面积，通常大于以坑塘为主的水利设施，分维值间于1-2之间，偏向于面状分布. 进一步认为，大比例尺土地利用图上，由有限个、分离的、小面积图斑构成的地类，计盒维数趋于1，大面积、连片分布的地类趋于2.

3.2.2 分维值与面积、面积比重的关系

分别统计了搬罾、凤山5种土地类型的面积、在全乡镇(样区)中的面积比重以及他们的分维值. 对于搬罾而言，不同类型土地的面积和面积比重大小排序依次为：耕地>建设用地>林地>宅基地>水利设施，而其分维值同样遵循这个顺序. 凤山土地类型的面积和面积比重大小排序依次为：耕地>林地>建设用地>宅基地>水利设施，分维值也遵循同样的大小顺序. 可见，在同一个空间范围上，面积或面积比重越大，其分维值越大. 因空间范围相同，面积和面积比重的大小反映空间占据度的大小，将土地利用图斑面积在行政区(或研究区)总面积中的比重定义为“占据度”. 则在相同或相近的空间范围上，土地利用的空间占据度越大，分维值越大；反之亦然. 这一现象与相关文献[1, 14]的研究结论类似.

但是面积、面积比重(占据度)与分形维数并不遵循简单、统一的函数关系(图1、2). 如凉水井村与蔡家沟村具有相近的耕地面积值，分别为116.02和115.69hm2；但它们对应的分形维数分别为1.7918和1.8422，相差较大. 搬罾各村总体的耕地比例与凉水井村的耕地比例，分别为77.14%和77.00%，相差微弱；但它们所对应的分形维数分别为1.7275和1.7918，差异较大. 由此认为土地图斑的分维值还与更多因素相关.

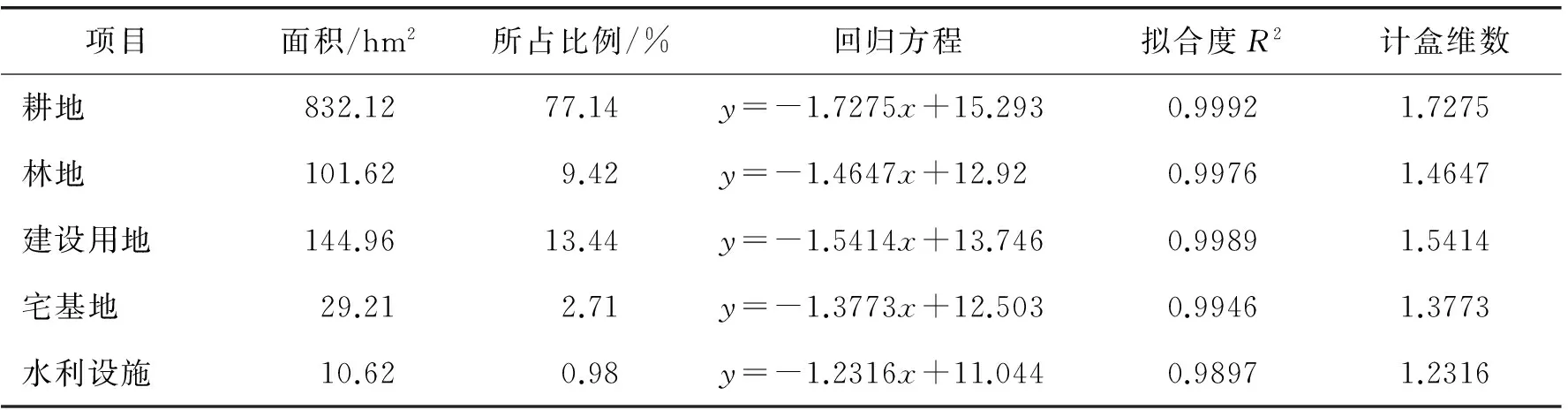
表2 搬罾镇不同土地利用类型计盒维数计算结果

表3 凤山乡不同土地利用类型计盒维数计算结果

表4 搬罾镇4个村耕地计盒维数计算结果

表5 凤山乡4个村耕地计盒维数计算结果

3.2.3 分维值与图斑在外接正方形空间填充度的关系

计盒维数的计算以图斑的最小外接正方形为基础. 因此把凉水井村、蔡家沟村和搬罾镇的耕地图斑外接正方形缩放到同样显示大小的情形下进行对比(图3). 搬罾镇的耕地呈东北-西南向带状延伸，对所在外接正方形空间的填充程度(以下简称“填充度”)最小，而其分维值也最小；与蔡家沟相比，凉水井因北侧碎小飞地的存在而降低了其对空间的填充度，分维值相对偏小. 由此推测，分维值也是图斑对其外接正方形空间填充度的度量：越接近于充满整个外接正方形区域，分维值越大；反之亦然. 分维值对填充程度的量化，与外接最小正方形的实际大小无关.

这一结论与前两节结论并不矛盾. 填充度越大，即图斑越趋于充满整个外接正方形，图斑的轮廓也越接近于满铺的正方形，分维值趋于2. 这与3.2.1节结论相同. 同时土地图斑的占据度和填充度，都是对其面积的刻画，二者紧密联系. 同一空间范围内不同土地类型外接正方形相同或相近，占据度越小则填充度也越小，相应的分维值也越小. 但在不同空间范围上，占据度与填充度并不遵循这个特征；较小的占据度有可能对应于较大的填充度，从而存在较高的分维值. 如蔡家沟村耕地在该村的占据度为67.37%，小于耕地在搬罾全镇的占据度77.14%；但据图3，显然蔡家沟村耕地图斑填充度相对更大，对应的分维值也更大.

所以占据度仅适用于同一空间范围内不同土地类型图斑的比较；填充度则同时适用于相同和不同空间范围的情形.

同时注意到，基于图斑最小外接正方形量化的填充度，可以反映土地类型对空间的充分利用程度. 土地类型的分维值越大，该类型土地越是趋向于充满最小外接正方形，对空间利用更充分、积聚. 在两个乡镇中，耕地最接近满铺分布，分维值最高；宅基地、水利设施都呈离散点分布，分维值最低. 其他类型介于二者之间.

3.3 地形和农户户数对土地利用分维值的影响

土地利用是自然和社会要素综合作用的产物，分维值在理论上会受这两方面的影响. 在丘陵地区村镇尺度上，地形影响土地的利用方式及其空间展布，是最显著的自然条件. 农户是土地经营的最基础单元，其经营目的和方向的差异会影响土地利用类型的多样性，是最直接的社会因素之一. 尝试采用回归分析，讨论地形、农户户数与耕地分维值之间的关系.

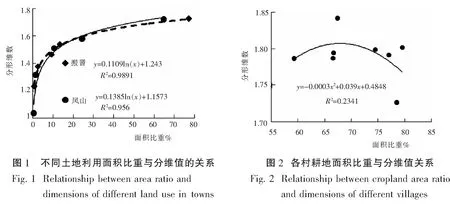
表6整理了研究区内8个村的地形特征值、农户户数和对应村的耕地分维值. 分别利用高程标准差、平均高程和户数，与耕地分形值进行不同模型的回归拟合；并整理对应的拟合度参数R2(表7). 结果表明，三种指标拟合的R2最大值依次为：0.0337、0.0196、0.2026.R2都无法通过显著性检验，在统计意义上可视为这三个指标与耕地分维值几乎不相关. 这一观察结果与相关研究[5, 15, 16]结论明显不同.

表6 各村地形特征值、户数和耕地分形值统计

表7 地形特征、农户户数与耕地分维值进行回归分析的拟合度R2

研究区内的耕地图斑分维值与地形、农户户数几乎不相关，原因在于：1.用于讨论的地类类别比较粗. 通常地形通过影响水热再分配而显著地影响到旱地、水田、水浇地的空间分布；但把上述类别合并为耕地而作为一个整体参与讨论时，地形在低丘地貌区的影响在分维值中表现并不明显. 2.研究区人口密集，土地开垦彻底，各村的耕地占据度都很高. 则各村耕地分维值可能更多取决于村界的形状. 但村界的划定有复杂的历史和社会因素影响，不单取决于地形和户数.

4 结 论

(1)川中丘陵地区在村镇尺度上，土地利用空间分布具有显著的分形特征，不同土地类型计盒维数介于1-2之间；可以利用分维值对土地利用空间分布的复杂性进行量化和分析.

(2)计盒维数能表征土地利用图斑的形状特征. 大比例尺土地利用图上，由有限个分离的小面积图斑构成的地类，计盒维数趋于1；大面积连片分布的地类趋于2. 丘陵地区以坑塘为主的水利设施分维值趋于1；耕地趋于2；林地和宅基地等介于1-2之间.

(3)计盒维数能指示土地利用图斑的空间占据度和填充度，分维值越大，则占据度和填充度越大. 但占据度仅适用于相同或相近的空间范围上土地类型之间的比较；填充度则同时适用于相同和不同空间范围上的比较.

(4)计盒维数能表征土地类型对空间的充分利用程度. 对限定空间的利用程度越充分，土地分布越趋向于填满图斑的最小外接正方形，分维值越大.

(5)研究区内土地利用的计盒维数与地形、农户户数之间未检测出明显的相关关系. 土地利用分维值受哪些因素显著影响，需要进一步研究.

[1] 李保杰, 顾和和, 纪亚洲. 矿区土地利用分形特征动态变化[J]. 农业工程学报, 2013, 29 (21): 233-240,302.

[2] 王聃同, 袁春, 周伟, 等. 基于分形理论的土地利用景观格局特征分析——以湖北省咸丰县为例[J]. 资源与产业, 2012, 14 (3): 147-152.

[3] 张珂, 赵耀龙, 付迎春, 等. 滇池流域1974年至2008年土地利用的分形动态[J]. 资源科学, 2013, 35 (1): 232-239.

[4] 张晶, 濮励杰, 朱明, 等. 矢量和栅格数据土地利用结构分维值比较——以苏州为例[J]. 地理科学进展, 2013, 32 (6): 932-939.

[5] 杨洋, 毕如田. 黄土高原典型地貌类型的土地利用分形特征[J]. 地理与地理信息科学, 2011, 27 (1): 101-104.

[6] 刘晓辉, 吕宪国, 董贵华. 分维模型在土地利用研究中的应用[J]. 地理科学, 2008, 28 (6): 765-769.

[7] 于 淼, 李建东. 基于RS和GIS的桓仁县乡村聚落景观格局分析[J]. 测绘与空间地理信息, 2005, 28 (5): 56-60.

[8] BENGUIGUI L, CZAMANSKI D, MARINOV M, et al. When and where is a city fractal[J]. Environment and Planning B: Planning and Design, 2000, 27 (4): 507-519.

[9] 朱晓华, 蔡运龙. 中国水系的盒维数及其关系[J]. 水科学进展, 2003, 14 (6): 731-735.

[10] 角媛梅, 杨丽萍. 基于遥感和 G I S的元阳梯田分形美的多尺度研究[J]. 山地学报, 2008, 26 (3): 339-346.

[11] 林志垒, 晏路明. 基于GIS和盒计数法的景观类型分形研究[J]. 亚热带资源与环境学报, 2009, 4 (1): 9-14.

[12] 张世熔, 龚国淑, 邓良基, 等. 川西丘陵区景观空间格局分析[J]. 生态学报, 2003, 23 (2): 380-386.

[13] 李首成, 刘文全, 程序, 等. 基于高分辨率卫星图的川中丘陵区村级景观格局特征研究[J]. 应用生态学报, 2005, 16 (10): 1830-1837.

[14] 施泽进, 罗蛰潭, 彭大钧, 等. 四川盆地油气田空间分布的分形特征[J]. 地球科学——中国地质大学学报, 1995, 20 (1): 68-72.

[15] 宋利珍, 常庆瑞. 秦巴山区不同地貌类型土地利用分形研究[J]. 江西农业学报, 2011, 23 (10): 154-157.

[16] 徐建华, 方创琳, 岳文泽. 基于 RS与 GIS的区域景观镶嵌结构研究[J]. 生态学报, 2003, 23 (2): 365-375.

Fractal Geometry Analysis of Spatial Distribution of Land Use in Central Sichuan Hilly Region

DUAN Han-ming, ZHANG Xue-mei

(College of Land and Resource, China West Normal University, Nanchong 637009, China)

Fractal dimension of different land-use types was computed by a box-counting method with Banzeng and Fengshan towns of Nanchong as the sample areas of central Sichuan hilly region. Then,dimension’s implications about land use spatial distribution and its influence factors were analysed. Results indicate that land use is clear fractal in town and village scale. The fractal dimension of different land-use types is between 1 and 2; irrigation facilities’ dimension tends to be 1 and plough’s dimension tends to be 2. Fractal dimension could indicate the occupancy degree of one land-use type in the total study area or administrative area and the fullness degree in external min square. A bigger fractal dimension means larger occupancy degree and larger fullness degree. No palpable correlation has been detected out between topography factor, number of farmer households and fractal dimension.

fractal; Box-counting dimension; land use; spatial distribution; central Sichuan hilly region

1673-5072(2015)01-0077-07

2014-11-12

西华师范大学科研启动基金项目(08B003); 南充市“十二五”社科规划课题(NC2013C014)

段含明(1983-),男,四川武胜人,西华师范大学国土资源学院讲师,主要从事遥感及GIS应用研究.

P91

A