基于弧长法的桁架臂结构全过程非线性稳定性分析

王殿龙，骆 广，王 欣，高顺德

（大连理工大学 机械工程学院，辽宁 大连 116023）

在履带起重机日益向着大型、高耸、轻柔化、格构式方向发展的过程当中，其稳定性问题也日显突出［1］.稳定性问题不同于强度问题，构件失稳往往比强度破坏出现得更隐蔽，破坏性也更大.

履带起重机桁架臂结构的稳定性问题常用解法有静力平衡法、缺陷法、振动法和能量法［2］.但是，这些方法常以“抽象梁”作为研究对象，对于工程实际中具有复杂空间结构的臂架而言，此举很难完全体现臂架杆件空间交错从而互相耦合对其稳定性产生的影响［3］.因此，在实际工程应用中，大量使用的是求解稳定问题的数值方法，其中采用有限元单元法对复杂构件的稳定性问题进行求解应用最为广泛［4－5］.

稳定性问题在有限元中有两种解法.一种是线性稳定性，即特征值屈曲，其特点是求解相对简单和高效，在工程中运用也较多［6］.但是，线性稳定性无法考虑构件的初始缺陷、载荷分布、材料非线性等对稳定性的影响.由于小变形理论的限制，线性稳定性分析也无法考虑几何非线性对结构承载能力的削弱，其结果相对乐观.另一种是非线性稳定性，它采用非线性迭代进行全过程分析，通过求解不同载荷状态下结构的变形响应，绘制结构的载荷－位移（F－u）全过程曲线，从全过程曲线分析中得到结构的极限载荷.该方法考虑了初始缺陷、载荷分布和非线性对稳定性的影响，分析结果更符合工程实际［7－8］.履带起重机的桁架臂多为大长度的空间格构式结构，其稳定性是典型的非线性问题，本文针对该问题，本文使用弧长法［9－11］，考虑臂架初始缺陷、载荷分布和几何非线性，对臂架进行了载荷－位移的全过程非线性稳定性分析.通过分析臂架的载荷－位移全过程曲线，并和线性稳定性分析结果进行对比，得到了较为符合工程实际的臂架极限载荷，验证了全过程非线性分析对于分析复杂构件的实际意义，可为工程设计和评估提供有力根据.

1 稳定性分析的有限元理论

1.1 线性稳定性分析

有限元中结构的增量平衡方程可表示为：

式中：［K0］为结构的弹性刚度矩阵；［Kσ］为结构的初应力刚度矩阵；［Kε］为结构的初应变刚度矩阵.

根据失稳的定义，结构屈曲时载荷增加一个很小的量，其位移即急剧增加，因此结构屈曲时上述平衡方程中｛Δue｝必有非零解，从而det（［K0］＋［Kσ］＋［Kε］）＝0.在结构的线性屈曲分析时假设结构屈曲前处于初始平衡状态，因此上式中的［Kε］＝0；在小位移情况下，［Kσ］与应力水平成正比，应力与外载荷也为线性关系.假设结构施加一个参考载荷Fref，［Krefσ］为参考载荷对应的初应力矩阵.令Fcr＝λ·Fref为屈曲时的载荷大小，根据应力与载荷的线性关系，则屈曲时的应力矩阵［Kcrσ］可表示为：

所以经典线性稳定理论的平衡方程为：

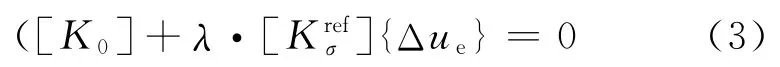
方程（3）有非零解的充分必要条件是det（［K0］＋λ·）＝0.在n个自由度的有限元模型中，产生λ特征值的n阶多项式，这种情况下特征值向量｛Δu｝n表示屈曲时叠加到系统上的变形，特征值λ与参考载荷Fref相乘即为失稳载荷Fcr.

由于无法考虑初始缺陷、载荷分布和非线性对稳定性的影响，线性稳定性只对载荷－位移曲线如图1的结构（即屈曲前变形很小，屈曲后位移急剧增加）取得较好的效果.由于假设结构失稳前处于小变形状态，忽略了屈曲前变形的影响，常常会导致过高估计结构的临界载荷［12］.特征值屈曲分析用于预测一个理想弹性结构的理论屈曲载荷，相当于教科书里的弹性屈曲（欧拉屈曲）分析方法.

图1 线性稳定性分析载荷－位移（F－u）曲线Fig.1 Load－displacement curve of linear stability

1.2 非线性稳定性分析

在实际的工程问题中，由于结构往往具有初始缺陷（如自重引起的初始下挠，制造和装配误差等），载荷分布也不是完全理想，再加上非线性的影响（材料非线性，几何非线性），其实际的载荷－位移曲线常如图2所示.

图2 非线性稳定性分析载荷－位移（F－u）曲线Fig.2 Load－displacement curve of nonlinear stability

在到达极值载荷A点之前，结构变形随着载荷的增加也在逐渐增加，在载荷达到极值载荷A之后，即使载荷不变甚至减小，结构的变形仍然在增加，此时结构失去了承担载荷的能力；随着变形的继续增大，结构有可能重新获得承担载荷的能力，如图2中的AB段，该情况多出现于网壳结构中；与此同时，结构也可能完全丧失了承受载荷的能力，如图2中AC段所示，该情况多出现于细长桁架结构中.这一变化过程可以用结构的载荷－位移曲线清晰地表达出来.结构的载荷－位移曲线可以通过对结构进行非线性稳定性分析获得.

在非线性计算中，常见的迭代方法有摄动法、载荷增量法、位移增量法和弧长法.摄动法理论复杂不便于实际操作［13］.载荷增量法采用载荷作为增量，逐步增加载荷到预定值，但是当载荷达到极值点附近时，刚度矩阵接近奇异，迭代不易收敛.除此之外，迭代过程中载荷只能增加不能减少，从而使得采用该方法无法获得结构在屈曲后的载荷－位移曲线（即图2中A点以后的曲线）.位移增量法使用位移作为迭代增量，同样会因为在极值点附近由于刚度矩阵奇异而导致不易收敛的问题.虽然以位移作为迭代增量可以使迭代越过极值点（即图2中A点）而跟踪结构失稳后的载荷－位移曲线，但是这需要预先知道结构的变形模式，而在实际工程问题中结构的变形模式常很难确定.因此，位移增量法在实际过程中也难以操作.弧长法由于添加了弧长约束，在迭代过程中可以自动生成载荷增量以寻求收敛，甚至可以生成负的载荷增量来完成自动卸载，因而是结构稳定分析中广泛采用的方法［14－15］，其迭代过程如图3所示.

图3 弧长法的收敛过程Fig.3 Arc－length iteration process

图3表示使用弧长法进行非线性迭代求解的迭代过程.具体的计算过程如下：

（1）载荷通过增量形式逐渐施加.

（2）在载荷增量每一子步迭代中完成平衡迭代，使增量方程达到平衡.

（3）求解以下增量平衡方程：

其中：［KT］为切线刚度矩阵；｛Δu｝为位移增量；｛Fn｝为外部载荷向量；Fnr为内部节点力向量；λ（－1＜λ＜1）为载荷因子.其中位移增量｛Δu｝、载荷因子λ、弧长半径l满足以下约束关系：

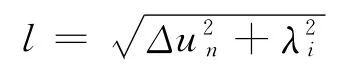
（4）进行迭代，直到λ｛Fn｝－｛Fnr｝在允许容差内.

2 履带起重机桁架臂在有限元中的表达

履带起重机桁架臂多为无缝钢管焊接的空间桁架结构，弦杆和腹杆之间可以传递力和弯矩，因此采用 “梁”单元建模.其标准节是等截面桁架结构，底节和顶节是变截面桁架结构，各个臂节之间通过铰耳联接.通过增减标准节的个数来改变臂架长度.底节通过两个铰耳与下车铰接，顶节前面一般会连接带有滑轮组的臂头.臂头通过拉板连接到桅杆上，收放变幅钢丝绳完成同一个臂长下的变幅操作，其典型结构如图4所示.拉板只受拉，采用“杆”单元建模.建模时保留结构之间的空间位置关系以更好地反映实际模型受力情况.

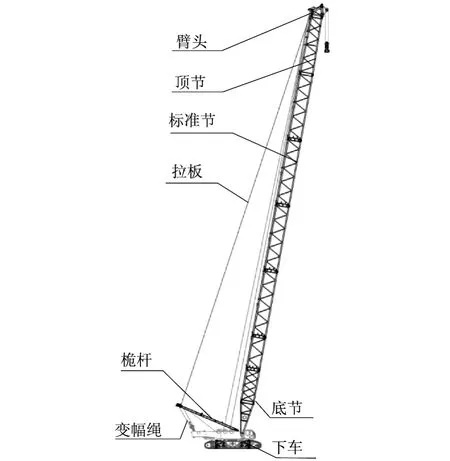
图4 履带起重机结构图Fig.4 Crawler crane

对履带起重机桁架臂而言，初始缺陷包括制造和安装误差、自重引起的初始下挠等.由于制造和安装误差具有不确定性，且在分析时可用侧载或侧向弯矩代替，所以本文中的初始缺陷仅指桁架臂自重引起的初始下挠.在线性稳定性分析中由于无法考虑初始缺陷，所以桁架臂的重力以外载荷方式均布作用在桁架臂上.在非线性稳定分析中，先计算桁架臂自重引起的下挠并将其更新到桁架臂模型，再在此基础上施加吊载进行后续分析计算.取桁架臂根部铰点为原点o，水平向右为x轴正方向，垂直向上为y轴正方向，z轴正向垂直xoy向外.如图5所示，底节根部铰耳只放开绕着铰耳轴线的旋转（铰点A，B约束ux，uy，uz，rotx，roty），拉板根部铰点施加全约束（铰点C，D 约束ux，uy，uz），吊载Q 和侧载F都施加在臂头上的吊载点，如果施加侧载，则侧载的大小结合国家标准和常规使用情况综合确定，取值F＝Q×tan 2°.本文中的载荷以及最后分析得到的极限载荷均指桁架臂吊载.

图5 载荷约束示意图Fig.5 Load and constraint

对于大臂长而言，桁架臂稳定性是典型的非线性问题，在桁架臂结构中具体表现为材料非线性和几何非线性.本文中只考虑几何非线性，即大变形对桁架臂稳定性的影响，因为：（1）如果同时考虑几何、物理两种非线性，所需计算时间将成倍增加，对于大规模的分析来说很困难；（2）桁架臂结构的正常工作状态是在弹性范围内，材料非线性对结构的影响实际上是使结构承载力的安全储备稍有下降，对这种影响已有可能从定量上做出适当判断.随着研究工作的进一步深入，再适时引入材料非线性进行计算.

3 算例分析

3.1 算例参数和加载信息

以750t级履带起重机的84m主臂为研究对象，主要参数为：弦杆管径×壁厚＝φ219.7×20mm，材料为FGS90WV；腹杆管径×壁厚＝φ114.3×5／6.3mm，材料为FGS78WV；标准节截面尺寸为2800mm（宽度方向）和2600mm（高度方向）；拉板截面积之和为4680mm2.该臂长属于大臂长，此时臂架是“细长结构”，几何非线性明显.

选择44m幅度工况为例，分3种情况进行加载：无初始缺陷工况；有初始缺陷（即桁架臂自重引起的初始变形）工况；有初始缺陷＋有水平侧载Q×tan 2°工况.加载情况如表1所示.对这3种工况都分别进行线性稳定性和非线性稳定性分析，以便进行结果对比.其中关于载荷的处理如上节所述.

表1 3种工况的加载信息Tab.1 Load information of three conditions

3.2 线性稳定性分析计算结果

对桁架臂进行线性稳定性分析，将计算得到的稳定性系数和当前施加的载荷相乘即可直接得到其屈曲载荷.工况1施加任意载荷后可以直接用稳定性系数和当前施加的载荷相乘计算得到屈曲载荷.但是工况2和工况3中，如果还是采用此方法，那么初始缺陷（重力）也会被乘以稳定性系数，显然这样与实际情况不符.实际计算中，施加重力并保持不变，通过不断调整施加的载荷大小使计算得到的稳定性系数接近于1就可以避免这个问题.计算后得到工况1的屈曲载荷为460.2t；工况2屈曲载荷为436.5t；工况3屈曲载荷为435.7t.

在线性稳定性分析中，未考虑初始缺陷（重力）计算时，重力是当作一个外力载荷被施加到臂架上，因此有初始缺陷的临界载荷要略小于无初始缺陷的临界载荷.从工况2和工况3的计算结果可知，有、无侧载的线性稳定性计算结果差值仅为0.18%，侧载对稳定性的影响几乎为零，这是由于线性稳定性的理论仅考虑臂架轴线方向的载荷所造成的.显然这是不合实际的，这也从另一个角度说明进行非线性稳定性分析的必要.

3.3 非线性稳定性分析计算结果

图6 无初始缺陷（工况1）的全过程曲线Fig.6 Full－range curve without initial imperfection

图6为无初始缺陷（工况1）的全过程曲线，以综合位移u为例进行分析.由图6可见，随着载荷的不断增加，桁架臂变形逐渐增大，伴随着桁架臂位移的增大，图中曲线斜率越来越小，其载荷与位移之间的几何非线性关系也体现得越加明显.当载荷增加到390.3t（对应于图6中ux，uy，uz，u曲线中的拐点Ax，Ay，Az，A）时，载荷达到臂架抵抗外载荷的最大值，此时结构发生失稳.在结构失稳后，总体而言，结构抵抗外载荷的能力急剧下降，即使载荷不再增加，桁架臂变形却迅速增加，承担外载荷的能力急剧下降.失稳后，载荷减小会出现桁架臂变形的短暂减小，但是这个过程极为不稳定和短暂，随后桁架臂会再次进入变形增加阶段，如图6中ABC段曲线所示.桁架臂在失稳后可能会发生局部杆件失稳，造成载荷重分配，从而在载荷－位移全过程曲线中形成一个封闭的环，如图6中CDE段曲线所示.但是，这种影响是极为有限的，桁架臂变形在总体上依然在继续增加，同时承担外载荷的能力也在迅速下降.

图6中的ux，uy是结构在变幅平面（xoy平面）的位移分量，在该平面内有载荷作用，再加上拉板的变形造成臂架“向前探”，所以，x和y方向的位移是逐渐增加的.在载荷达到拐点390.3t后，在变幅平面内载荷即使不再增加，臂架变形却迅速变大，此时认为臂架在变幅平面内失稳.在回转平面（xoz平面，uz曲线），桁架臂相当于经典的欧拉梁轴向受压的情况，属于典型的压杆失稳，所以在屈曲前z向位移几乎为0，在屈曲后z向位移急剧增加.这里用非线性全过程方法得到的载荷－位移曲线和经典欧拉梁轴向受压的屈曲过程吻合得很好.在载荷达到拐点390.3t后，臂架在回转平面内也开始失稳.综上所述，可以从图6中看出，载荷－位移全过程曲线中拐点的极大值390.3t即为臂架的极限载荷（x，y，z这3个方向上的极限载荷相同），超过此载荷，结构必然因变形过大而破坏.

图7为考虑桁臂架自重引起初始下挠造成桁臂架初始缺陷（工况2）的载荷－位移全过程曲线，此变形趋势和图6中相同，但该工况下桁臂架的极限载荷为372.1t.受桁臂架自重初始挠度影响，其极限载荷有所降低.

图7 有初始缺陷（工况2）的全过程曲线Fig.7 Full－range curve with initial imperfection

图8为考虑桁臂架自重引起初始下挠造成初始缺陷并且施加侧载（工况3）的载荷－位移全过程曲线，它们的总体变形趋势和图6基本相同，都是在达到曲线的拐点（图8中Ax，Ay，Az，A）之后，桁架臂载荷不再增加但变形却仍然迅速变大，结构失去承担载荷的能力.

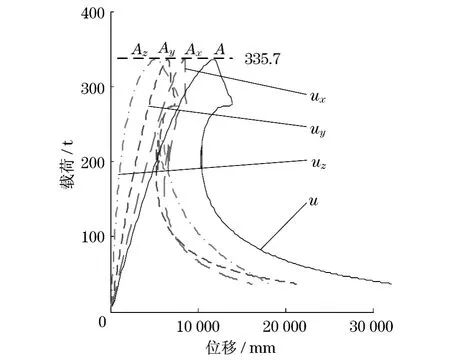
图8 有初始缺陷并加侧载（工况3）的全过程曲线Fig.8 Full－range curve with initial imperfection and side load

由于有侧载（z向施加载荷），所以在z方向的变形分量是逐渐增加而不是在失稳前几乎为零，这与x向和y向的整体变形趋势类同.同时由于x，y，z这3个方向上的位移互相影响，所以在曲线局部的趋势上与图6有所不同.该工况下桁臂架的极限载荷为335.7t，表明侧向载荷和变幅平面内存在初始缺陷时将进一步降低结构的稳定性.

图6～8都取桁架臂的吊载点作为观测点而得到其载荷－位移曲线.在本次分析过程中，还选取了桁架臂中部节点、桁架臂根部节点等其他观测点来绘制其载荷－位移曲线，所得曲线的趋势与图6～8中的趋势基本一样，得到的极限载荷也分别相同，表明结构是整体失稳，构件自身的变形要远小于其位移.由此可得桁架臂对应工况下的极限载荷分别是390.3，372.1，335.7t.

3.4 线性和非线性结果对比

将线性和非线性稳定性计算结果汇总，如表2所示.从对比结果可知，线性稳定性分析由于未考虑初始变形、载荷分布和几何非线性对稳定性的影响，其计算结果相对乐观，与非线性结果比较，两者的差值在本例中最大达到了29.79%.因此在实际的工程设计和评估中，进行非线性稳定性分析是非常必要的.

表2 线性与非线性稳定性分析结果对比Tab.2 Comparison of linear and nonlinear results

4 结语

本文以履带起重机桁架臂为研究对象，使用弧长法，考虑初始缺陷、载荷分布、几何非线性对桁架臂稳定性的影响，对桁架臂进行非线性分析，绘制出桁架臂的载荷－位移全过程曲线.通过分析载荷－位移全过程曲线，并和线性稳定性分析结果进行对比，得到了桁架臂较为真实的极限载荷.该方法可为工程设计和评估提供有力根据.

［1］王欣，高顺德.国外履带起重机的特点及国内市场现状［J］.建筑机械，2006（7）：12－16.WANG Xin，GAO Shunde.The characteristics of foreign crawler crane and domestic market status［J］.Construction Machinery，2006（7）：12－16.

［2］李双蓓，刘立国，倪骁慧.结构稳定性研究的现状和新方法的探索［J］.广西大学学报：自然科学版，2004（11）：107－110.LI Shuangbei，LIU Liguo，NI Xiaohui.The research present situation of structure stability and its new method［J］.Journal of Guangxi University：Natural Science，2004（11）：107－110.

［3］陆念力，王佳，兰朋.格构式构件整体稳定性分析的等效惯性矩法［J］.建筑机械，2008（8）：79－83.LU Nianli，WAND Jia，LAN Peng.Equivalent inertia moment method to the overall stability analyses of lattice type beam ［J］.2008（8）：79－83.

［4］张静.履带起重机臂架稳定性研究［D］.大连：大连理工大学，2009.ZHANG Jing.Stability analysis of crawler crane boom ［D］.Dalian：Dalian University of Technology，2009.

［5］SKRINAR M.Improved beam finite element for the stability analysis of slender transversely cracked beam－columns［J］.Computational Materials Science，2009（3）：663－668.

［6］马青.履带起重机臂架有限元简化模型稳定性分析［D］.大连：大连理工大学，2008.MA Qing.Stability snalysis of crawler crane boom system based on simple finite element model［D］.Dalian：Dalian University of Technology，2008.

［7］沈世钊.网壳结构的稳定性［J］.土木工程学报，1999（12）：10－18.SHEN Shizhao.Stability of shell structure［J］.China Civil Engineering Journal，1999（12）：10－18.

［8］王娜，陈昕，沈世钊.网壳结构弹塑性大位移全过程分析［J］.土木工程学报，1992（1）：19－26.WANG Na，CHEN Xin，SHEN Shizhao.Full－process analysis with plasticity and large displacement on shell［J］.China Civil Engineering Journal，1992（1）：19－26.

［9］RIKS E.An incremental approach to the solution of snapping and buckling problems［J］.Solid Structures，1979，15：529－551.

［10］RAMM E.Strategies for tracing the nonlinear response near limit points［C］∥Nonlinear Finite Element Analysis in Structural Mechanics.［s.l.］：［s.n.］，1981：63－89.

［11］CRISFIELD M A.An arc－length method including line searches and accelerations［J］.Int J Num Mech Eng，1983，19：1269－1289.

［12］王勖成.有限单元法［M］.北京：清华大学出版社，2003.WANG Xucheng.Finite element method ［M］.Beijing：Tsinghua University Press，2003.

［13］陈务军，关富玲，强士中.桥梁结构稳定分析的一种新方法［J］.桥梁建设，1996（4）：10－12.CHEN Wujun，GUAN Fuling，QIANG Shizhong.A new method for analysis of stability of bridge structure［J］.Bridge Construction，1996（4）：10－12.

［14］沈世钊.陈昕.网壳结构稳定性.［M］.北京：科学出版社，1999.SHENG Shizhao，CHEN Xin.Stability of shell structure［M］.Beijing：Science Press，1999.

［15］蒋凤昌，朱慈勉，薛剑胜，等.基于弧长法的钢筋屈曲承载力非线性分析［J］.建筑科学，2007（11）：9－12.JIANG Fengchang，ZHU Cimian，XUE Jiansheng，et al.Nonlinear analysis of load－carrying capacity for bar buckling based on arclength method［J］.Building Science，2007（11）：9－12.