一种数字混沌加密系统的嵌入式仿真实现
2015-03-14牛青
牛 青
(贵州广播电视大学,贵州 贵阳 550022)
一种数字混沌加密系统的嵌入式仿真实现
牛青
(贵州广播电视大学,贵州 贵阳 550022)
摘要:海上舰船之间以及舰船与控制中心之间通信的加密及解密事关整个海战成败。本文对用于海上舰船通信加密系统中热门Baptista混沌加密算法进行了系统研究,分析在实际舰船通信系统中实现的利弊。针对Baptista算法在产生的混沌加密信号出现的周期规律性以及动力衰退性弊端,改进此算法,提出一种加强型控制位混沌加密算法。此算法通过增加控制位对混沌加密明文进行自适应控制,使其不规律改变混沌系统运行轨迹,克服Baptista算法的周期性以及动力衰退性。最后设计基于此算法的FPGA仿真系统,对其进行验证。
关键词:无线通信系统;混沌加密系统;Baptista;FPGA
0引言
随着通信以及计算机技术的飞速发展,无线通信技术在海军作战及指挥系统发挥着越来越重要的作用。而通信系统的加密技术,对防止敌方获取情报至关重要,也是战争成败的关键要素之一。如早期的经典加/解密标准DES、中期的加密标准AES等都对当时海面船舰作战指挥起到了重要作用,现代由于计算机的飞速发展,传统的加密算法已经很难满足现代海面作战指挥要求,利用统计分析交易进行机密。现代混沌及量子技术船舰通信加密系统得到了快速发展。
本文对混沌加密算法中的一种Baptista算法进行了深入分析。在理论上分析了该算法的明文性质。针对通信系统中生成序列精度的限制,使混沌加密系统具有长周期退化特性。针对此弊端,进而在Baptista算法的基础上提出了一种加强型控制位混沌加密算法,通过控制符对密码明文进行预处理及自反馈,改变了它的运行轨迹,进而规避了Baptista算法在数字通信领域中的劣势。在本文最后利用FPGA对此加密算法进行仿真,仿真结果表明此改进算法提高数字通信系统的保密性能,并具有更平滑的明文分布。
1Baptista算法解析
1.1 算法基本步骤
1)把加密之前的信号序列以一定位数n进行分组,以mi为分组后的第i组明文,其满足mi∈M(0,1,2,…,2n-1), M为明文幅度范围。
2)设Baptista混沌模型的初始系数为x0及加密密钥控制参数为b。
3)此混沌加密系统状态空间设为T,并且将此空间按照步骤1)中参数n划分2n个均匀空间,计为Ti,1,2,3,…,2n, 则空间T={T1,T2,…,T2n}。
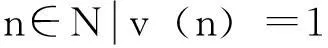
上述6个步骤是Baptista算法的基本步骤,其中对明文,即加密前信号满足如下定理:加密前的明文长度以及分组数与加密耗时是指数级递增关系[6]。
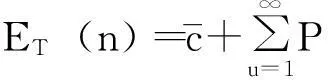
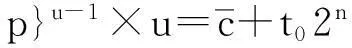
(1)
1.2 Bistista加密耗时与明文密文关系
表1给出了明文分组情况下,与密文下限比例仿真参数数据。
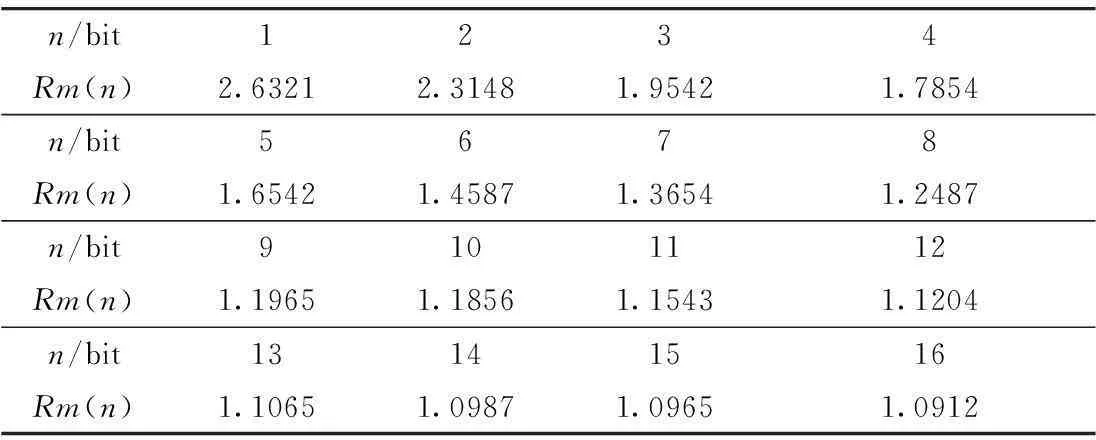
表1 仿真参数的设置
分析表1,设加密前的明文用16位bit表示,分别为1,2,3,…,16bit代表。当n=8时,Rm(8)=1.7854,本意为如果对明文的分组按照8 bit进行1组,则相应的密文与明文的比例则不低于表中的1.2487。
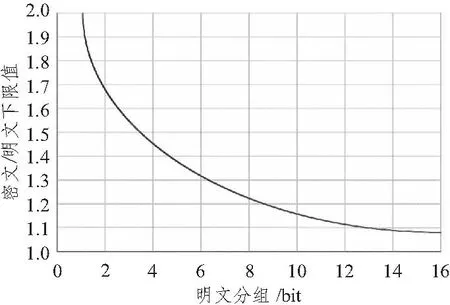
图1 密文明文比例期望值Fig.1 The proportion of clear text and cipher text
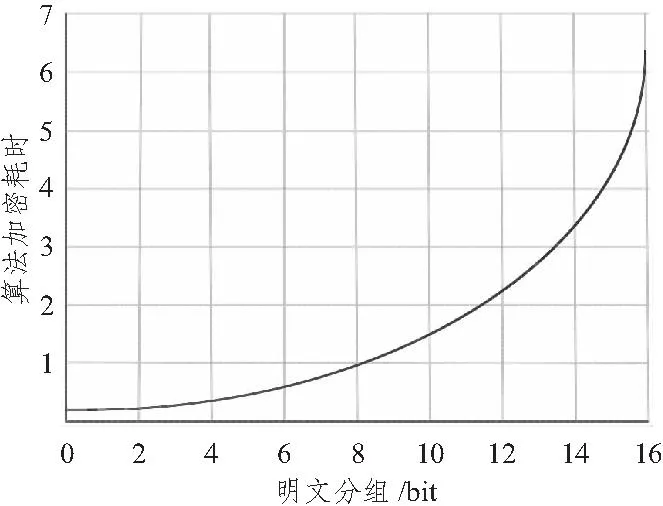
图2 算法的加密耗时曲线Fig.2 Curve graph of encryption time
图1是密文/明文比例的幅度值与明文分组位长的变化率图,图2是Baptista加密算法的耗时与明文分组位长的变化率图。可知,随着加密明文长度的递增,耗时将随之指数级增大,不利于算法实现。
2加强型控制位混沌加密算法
本文提出一种基于控制符的混沌加密算法,通过控制符控制迭代系统的复杂度,并且迭代过程产生下一步之前的控制符,这样既不会透露迭代次数信息,并且改变了原先的迭代轨迹,改善了Baptista混沌加密算法。
2.1 加强型控制位加密算法步骤
本算法利用混沌算法中的维度映射关系,设加密之前明文初值为x0∈(0,1), 初始控制位∂∈(0,1)。映射关系如图3所示。
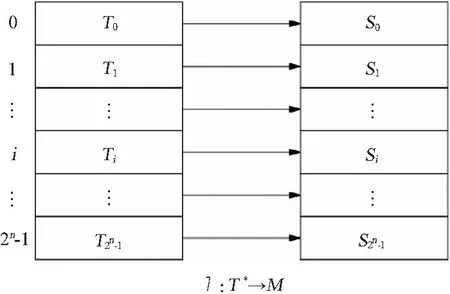
图3 数据映射示意图Fig.3 Diagram of data mapping
初始化阶段,系统加带加密的信号分组,按n为一组,假设共分为r组,用m=m1,m2,…,mr表示,则第i组满足mi∈{0,1,2,…,2n-1}, 同时将整个加密系统划成2n个子空间,则第i子空间Ti满足Ti=[xmin+i∂,xmax+(i+1)∂]。 分组后的子空间与整个加密系统子空间的对应关系为ε∈A={f:T*→M}, 且为唯一映射。
2.2 加强型控制位加密算法流程
加密算法流程如图4所示。
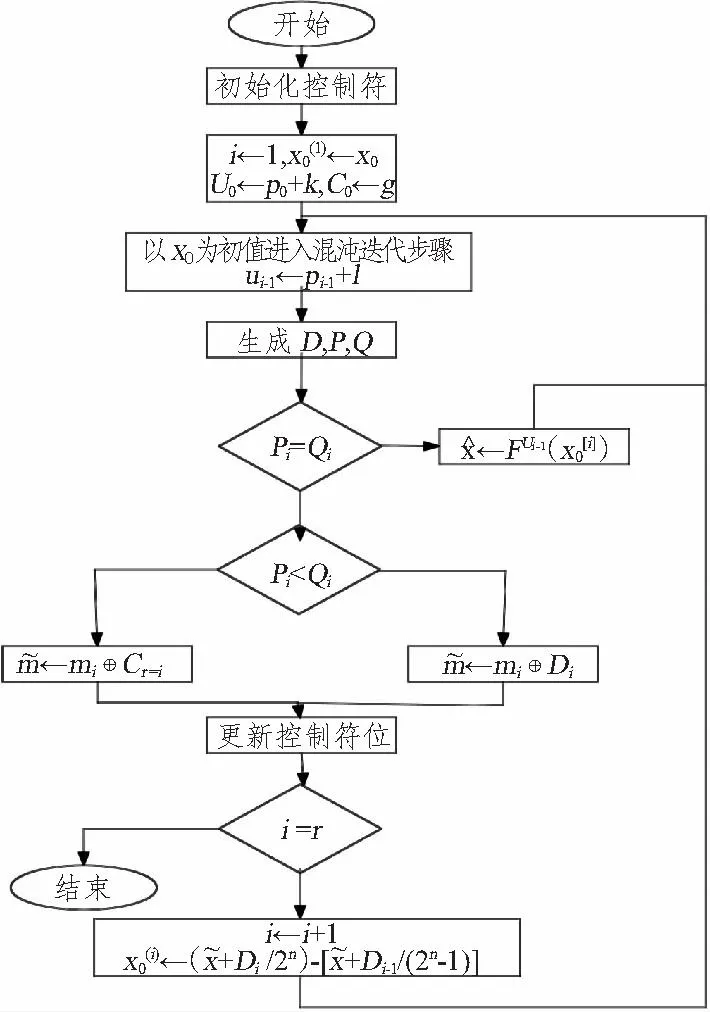
图4 加密算法过程流程图Fig.4 Flow chart of encryption algorithm process
加强型控制符加密算法的软件实现步骤如下:
1)设密钥第1次迭代初始值key={x0,b,p0},其中x0为明文第1组信号,b为此算法系统参数,p0为预计总的迭代次数。

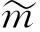
3基于FPGA的嵌入式系统
3.1 FPGA嵌入式系统模型
在利用此算法的加密通信系统选用了StratixⅡ型号的FPGA,用以实现加强型控制位加密算法,其他选用精度为24位的A/D转换器,以及通信中的平滑滤波器,系统仿真如图5所示。

图5 基于FPGA的嵌入式仿真系统Fig.5 Embedded simulation system based on FPGA
3.2 仿真结果及分析
本仿真加密前明文按照每8 bit作为1组,算法的混沌子空间置为Ti∈{0,1},系统参数b=0.666 777,待加密明文初始值设为x0=0.123 456,初始控制位p0=0.235 478, k=3,g=0进行仿真。
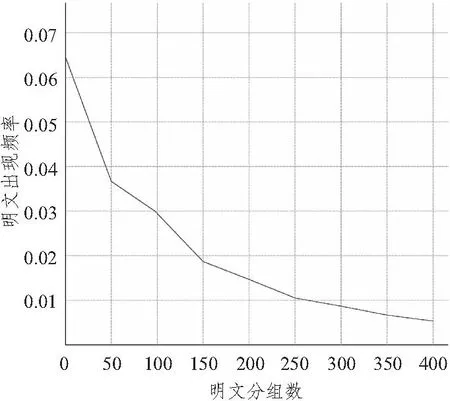
图6 算法加密后明文出现频率曲线图Fig.6 Curve graph of clear text appear frequency
图6给出了按照8 bit分组的加强型控制位加密算法中每组明文概率统计。可以看出,此算法随着分组数及加密前明文序列长度的增加,其明文的概率统计逐渐收敛,而香农定理表明对于所有的加密算法,都可以利用统计法来进行解密。所以此算法的抗统计性解密攻击能力随着明文序列增加而加强。提高了军事通信系统的保密性能。
4结语
本文在研究混沌技术在海面船舰加密通信系统中的应用,重点分析了Baptista算法的逻辑过程,并通过仿真分析了此算法的利弊。随后基于此提出了加强型控制位加密算法,通过控制符来对混沌系统的迭代过程进行控制,而控制符不仅起到了调节迭代次数的目的,同时使迭代过程更加具有不可知性,从而进一步提高了系统的安全性,克服了之前Baptista模型的混沌动力学的退化性。最后,设计了基于FPGA的嵌入式混沌加密通信系统,根据海面舰船无线通信实际经验设置初值进行了仿真实验,通过实验进一步验证了本算法的高保密性及可行性。
参考文献:
[1]冯登国.国内外密码学研究现状及发展趋势[J].通信学报,2002,23(5):18-26.
FENG Deng-guo.Statusquo and trend of cryptography[J].Journal of China Institute of Communications,2002,23(5):18-26.
[2]CUOMO K M,OPPENHEIM A V,STROGATZ S H.Synchronization of Lorenz-based chaotic circuits with applicat-ions to communications[C]//Circuits and Systems II: Analog and Digital Signal Processing, IEEE Transactions,1993:626-633.
[3]RAJAGOPAL S,NOH G K,SEUNG H P,et al.Chaotic UWB based system design for ultra low power body area networks[C]//Circuits and Systems Workshop,(DCAS),IEEE Dallas,2009:1-4.
[4]GE Xin-l,LIU Fen-lin,LU Bin,et al.Analysis of baptista-type chaotic cryptosystem.Multimedia and Expo[C]//IEEE International Conference,2007:891-894.
[5]周玉龙,杨松林,奚炜,等.基于遗传-混沌算法的船舶动力学性能综合优化研究[J].舰船科学技术,2005,27(4):18-21.
ZHOU Yu-long,YANG Song-lin,XI Wei,et al.Study on synthetical optimization of performance of ship dynamics based on GA-chaos[J].Ship Science and Technology,2005,27(4):18-21.
[6]陈旗,宋士琼,邓鹏飞.基于软件无线电技术的通信信号接收与数据采集系统研究[J].舰船科学技术,2010,32(5):59-63.
CHEN Qi,SONG Shi-qiong,DENG Peng-fei.Research of communication signal receving and data acquisition system based on technology of softwore vadio[J].Ship Science and Technology,2010,32(5):59-63.
[7]YONG Peng-xiao,YI Han.An encrypt approach using dynamic encrypt keys[C]//Machine Learning and Cybernetics,International Conference,2007:3273-3277.
[8]JIMENEZ W H,CORREA W T,SILVA C T.et al.Visualizing spatial and temporal variability in coastal observatories[C]//Visualization, VIS 2003,2003:569-574.
[9]MEDANY W M.FPGA remote laboratory for hardware e-learning courses[C]//Computational Technologies in Electrical and Electronics Engineering,2008:106-109.
A design of digital chaotic encryption embedded system
NIU Qing
(Guizhou Radio and TV University,Guiyang 550022,China)
Abstract:This paper first research chaotic encryption algorithm, especially Baptista algorithm using in marine wireless communication, and analyze the advantages and disadvantages of it. For the lower bound of expectation of the cipher-to-plaint, this paper propose a chaotic encryption algorithm based on control bit. The algorithm control the iteration process by control bit and change the trajectory of chaotic encryption algorithm. At last, design one marine chaotic encryption embedded system based on FPGA and simulate. The simulation results show that this algorithm improve the performance of chaotic encryption system.
Key words:wireless communication system; chaotic encryption system; baptista; FPGA
作者简介:牛青(1980-),女,副教授,研究方向为计算机技术。
收稿日期:2014-04-28; 修回日期: 2014-06-15
文章编号:1672-7649(2015)01-0196-04
doi:10.3404/j.issn.1672-7649.2015.01.042
中图分类号:TN92
文献标识码:A
