三维楔形体与圆锥体的砰击压力
2015-03-14司海龙李政杰胡嘉骏
司海龙,虞 昊,李政杰,胡嘉骏
(中国船舶科学研究中心,江苏 无锡 214082)
三维楔形体与圆锥体的砰击压力
司海龙,虞昊,李政杰,胡嘉骏
(中国船舶科学研究中心,江苏 无锡 214082)
摘要:基于有限元软件Fluent计算楔形体和圆锥体的入水砰击压力,并与试验结果进行比较,对于砰击压力分布及楔形体入水速度变化过程二者吻合较好。重点研究楔形体长宽比对砰击压力的影响。研究发现,楔形体长宽比对砰击压力影响较大,当楔形体长宽比大于3时,三维楔形体中横剖面的砰击压力计算可近似简化为具有同样剖面的二维楔形体入水问题。楔形体入水角对砰击压力极值的分布有很大的影响,相同入水速度条件下,楔形体的砰击压力极值比圆锥体的砰击压力极值大。
关键词:入水速度;砰击压力;长宽比
0引言
船舶在恶劣海况中航行时,船首会露出水面,在重新进入到水中时,会与水产生强烈的砰击,船首底部或外飘区域会产生过大的局部砰击压力,使得船舶结构发生损坏。 由船舶砰击引起的海难事故也时有发生,1994年,由于猛烈的砰击,“Estonia”号滚装船罩壳式首门被打掉在短时间内沉没,致使900多名船员及旅客丧生;1980年,“Onomichi-maru”号散货船同样由于船舶砰击的原因,造成严重的低周疲劳损伤,在太平洋海域沉没。因此,船舶砰击问题越来越引起人们的关注,提出合理的砰击载荷对于船舶设计具有重要意义。
物体入水砰击问题涉及到空气、水、固体三者之间的相互耦合作用,非常复杂。1929年,Von-Karman[1]针对水上飞机降落,首先对该问题进行了研究,将该问题简化为二维楔形体入水,利用动量理论,求得物体入水过程中的冲击力。Wagner[2]在该理论的基础上,考虑物体自由表面处的水面隆起效应,改善了浸湿半宽、附加质量、冲击力的求解,并求出了压力分布。Sheng-Lun Chuang[3]通过一系列具有不同入水角的楔形体的砰击入水试验,研究了空气垫对具有小角度入水角楔形体的砰击压力的影响,并得到楔形体入水最大砰击压力的计算公式。Zhao和Faltinsen[4]采用非线性边界元法计算了具有任意形状的二维剖面入水冲击问题,正确描述了砰击入水的飞溅现象。Ochi[5]对船模在静水和波浪中入水问题进行了试验研究,研究发现二维船模剖面在静水中的砰击压力几乎为三维船模在静水中压力和三维船模在波浪中砰击压力的2倍和5倍。Scolan和Korobkin[6]在Wagner理论基础上,忽略水的粘性和可压缩性,用解析法研究了三维钝形物体的入水砰击问题。国内的顾懋祥、程贯一和张效慈[7]较早地开展了这方面的研究,针对平头旋转壳撞水水弹性效应进行数值分析,并开展了相应的试验研究。胡嘉骏[8]基于线性切片理论对船舶表面入水点的砰击压力进行了预报。陈震[9]通过建立二维有限元模型,对平底结构的入水问题进行了详细的研究 ,发现空气层在平底结构入水的过程中作用很大,充当了缓冲垫的作用,大大减小了砰击压力的量值。
为了简化强度分析和便于结构设计,各船级社通过理论分析、实验研究和实船统计分析,给出了砰击载荷的简单计算公式。但随着社会的发展和需求,新型、高速和超规范船舶不断出现,船级社规范也难于满足需求。目前国内外对于砰击问题的研究大部分局限于二维物体或形状简单的三维物体,但砰击压力与物体的形状有很大关系,要给出合理的砰击载荷,必须要研究三维物体的砰击压力特性。随着计算机技术的进步与发展,运用CFD模拟形状复杂的三维物体入水问题成为可能。本文采用大型计算软件Fluent模拟三维楔形体和圆锥体的入水砰击压力,并与Zhao[10]的试验结果进行比较分析。
1物体入水砰击
1.1 问题描述
以楔形体和圆锥体为研究对象,分别计算其以某一速度自由落体或匀速进入到水中时各测量点的砰击压力。图1和图2分别为楔形体的俯视图和侧视图,入水角和长宽尺度和文献[10]中的楔形体试验模型保持一致,圆锥体的侧视图同图2。图3和图4分别为楔形体和圆锥体的入水示意图。

图1 楔形体俯视图Fig.1 Top view of wedge

图2 楔形体侧视图Fig.2 Side view of wedge

图3 楔形体入水示意图Fig.3 Water entry of wedge
图4 圆锥体入水示意图Fig.4 Water entry of cone
1.2 建立有限元模型
根据示意图在Gambit中建立有限元模型,如图5所示。在有限元模型中,楔形体和圆锥体及流体域的外表面和底面均设置为刚体,上表面设置为压力出口,即pressure-out,流体域的上层设置为空气,下层设置为水。在有限元模型中,在楔形体和圆锥体附近的流域采用细网格进行划分,较远的流域采用稀疏网格进行划分。

图5 三维有限元模型Fig.5 Three-dimensional finite element model
1.3 网格尺寸敏感度分析
为了消除网格尺寸对计算结果的影响,本文采用4种尺度的细网格,楔形体半宽与细网格尺寸比分别为62.5∶1, 87.5∶1, 125∶1, 175∶1。图6和图7为P2和P5在不同的有限元模型计算中的砰击压力随时间变化曲线。图8为4个模型中的各点的砰击压力极值,图9为各点砰击压力系数。由计算结果可以看到,尽管4个模型的网格尺寸不同,但各点的砰击压力随时间变化曲线吻合的非常好,砰击压力几乎同时达到极值,随着网格的细化,砰击压力极值虽有所增大,但幅度不大,可以认为砰击压力极值随着网格尺寸的减小逐渐平稳,趋于收敛。因此在这一比例范围内选择流域网格尺寸可以尽可能地减小网格尺寸对砰击压力计算的影响。本文选取模型三为基础计算模型,分别计算楔形体和圆锥体的入水砰击压力。
从P1到P5,砰击压力极值依次逐渐减小,主要由楔形体在入水过程中速度逐渐衰减造成;砰击压力系数依次有所小幅减小,但并没有因为入水速度的衰减而出现较大变化。
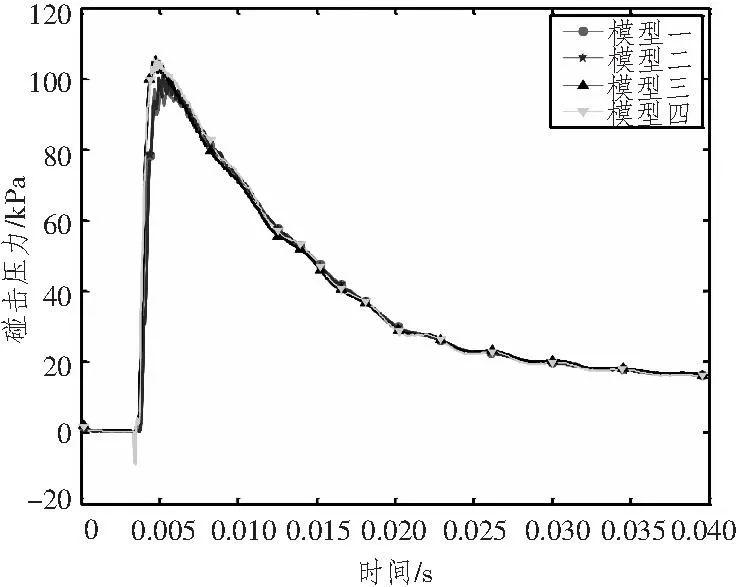
图6 P2点砰击压力随时间变化曲线Fig.6 Slamming pressure of P2
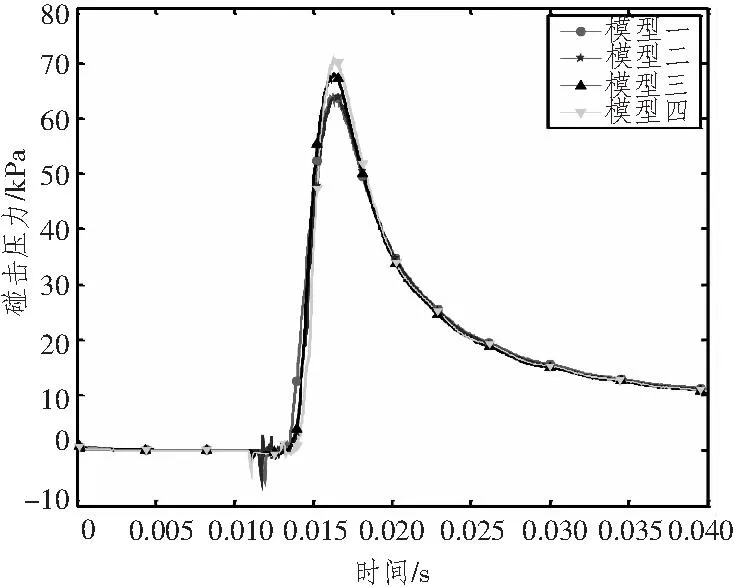
图7 P5点砰击压力随时间变化曲线Fig.7 Slamming pressure of P5
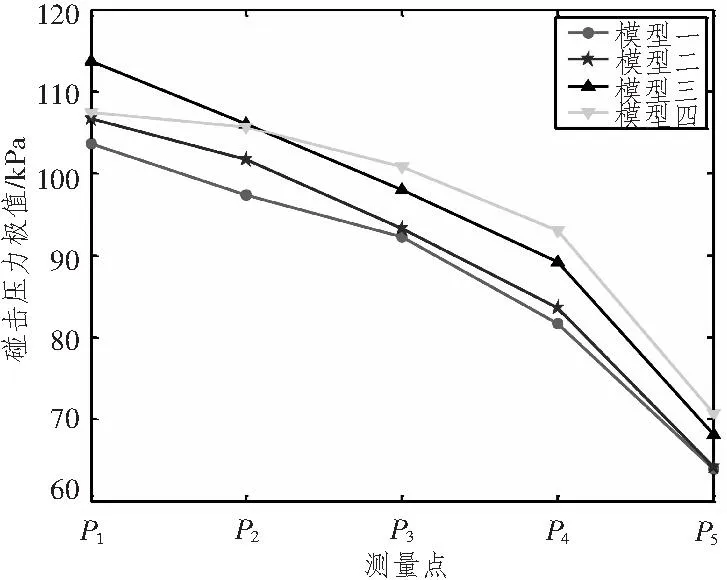
图8 砰击压力极值Fig.8 Extreme slamming pressure
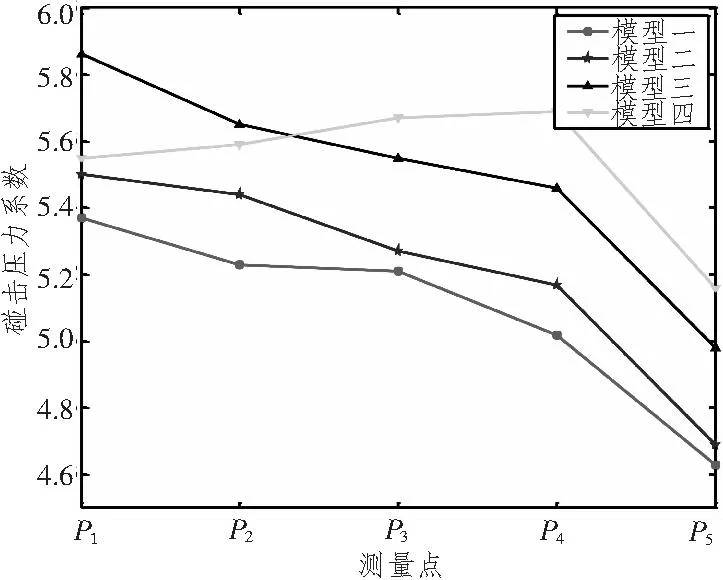
图9 砰击压力系数Fig.9 Slamming coefficient
1.4 比较分析
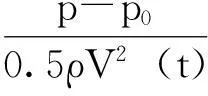

图10 楔形体入水过程中水面变化示意图Fig.10 Water entry of wedge
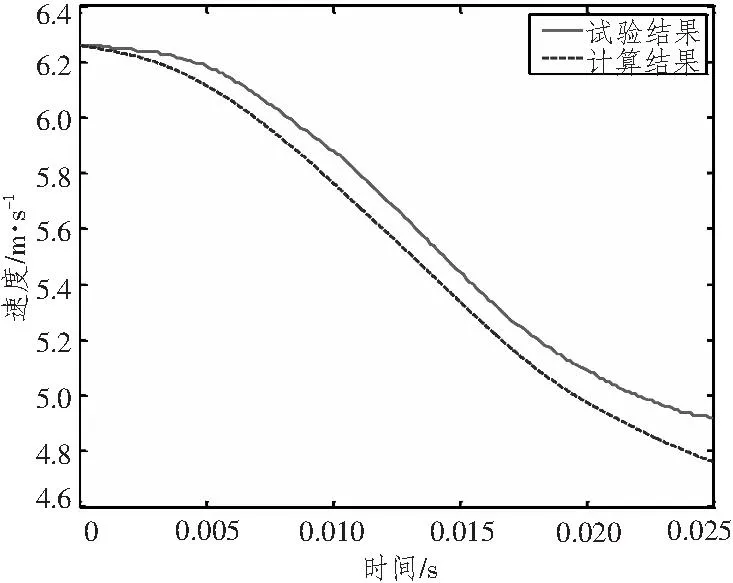
图11 楔形体入水速度变化曲线Fig.11 Wedge speed during entry water
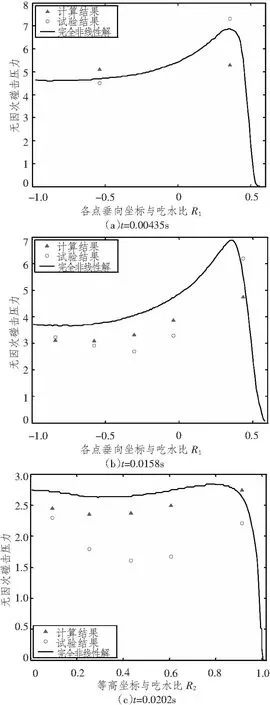
图12 楔形体入水无因次冲击压力Fig.12 Slamming pressure with out dimension
将计算结果与试验结果进行比较分析,可以看到由数值计算得到的入水速度略小于试验结果,各点的无因次砰击压力与试验结果有一定的差异,这可能是由Fluent处理自由液面的方式造成的。Fluent采用VOF方法捕捉自由液面,该方法比较适合处理自由液面连续变化的问题,但物体入水砰击为强非线性问题,物体入水瞬间有剧烈的液体飞溅现象,而这种现象在Fluent中则很难模拟。合理准确地模拟自由液面变化及液体飞溅现象,还需要进一步的深入研究与探讨。但大体上看,楔形体入水速度与实验结果变化趋势吻合的较好,计算结果在试验结果与完全非线性解之间变化,砰击压力分布与试验结果吻合较好,验证了模型三作为基础模型的合理性。
2楔形体长宽比对砰击压力的影响
以模型三作为基础模型,分别计算长宽比不同的楔形体自由入水时的砰击压力。楔形体入水角仍为30°,入水初始速度均为6.26 m/s,不同长宽比的楔形体质量按照长度方向单位长度质量等比例缩放,即m=241×L/2B。图13为各个测量点砰击压力随楔形体长宽比变化曲线,图15为长宽比不同的楔形体入水过程中的速度变化曲线。由计算结果可以看出,随着楔形体长宽比的增大,各点的砰击压力逐渐增大,P1,P2增大幅度较小,P3,P4,P5增大幅度较大;楔形体在入水过程中,下落速度逐渐衰减,楔形体长宽比越小,衰减程度越小,速度下降的越慢,楔形体长宽比越大,衰减程度越大,速度下降的越快。图14和图16分别为二维计算模型中各点的砰击压力极值和楔形体入水速度变化曲线,二维模型中的网格尺寸与三维有限元模型三的网格尺寸相等。比较二者结果,可以认为当楔形体的长宽比L/B>3时,三维楔形体中横剖面的砰击压力计算可近似简化为具有同样剖面的二维楔形体入水问题。
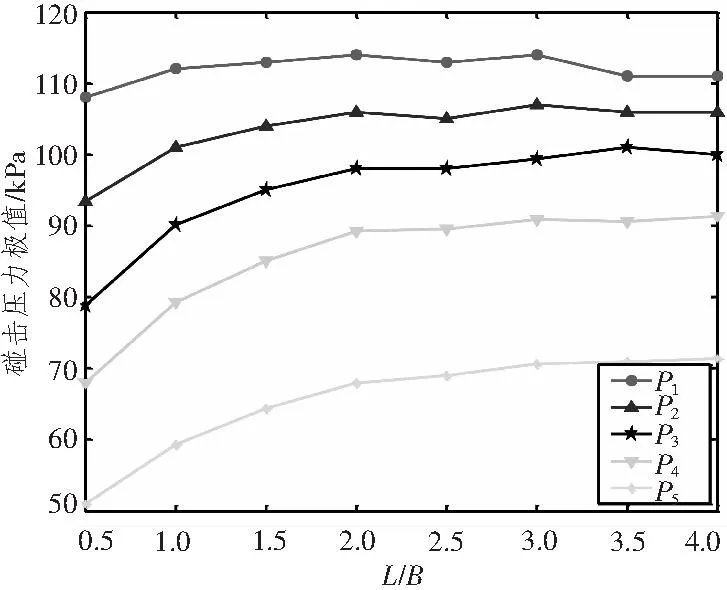
图13 各点砰击压力极值Fig.13 Extreme slamming pressure
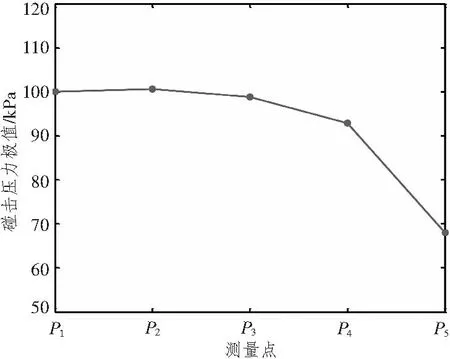
图14 二维模型中各点砰击压力极值Fig.14 Extreme slamming pressure of two-dimensional model
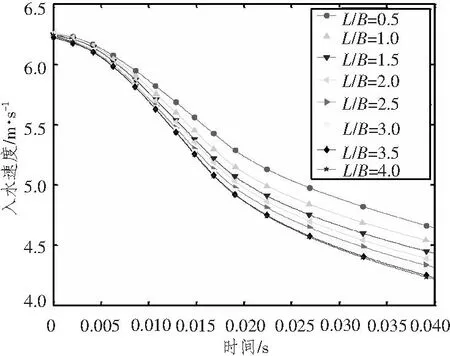
图15 楔形体入水速度变化曲线Fig.15 Wedge speed during entry water
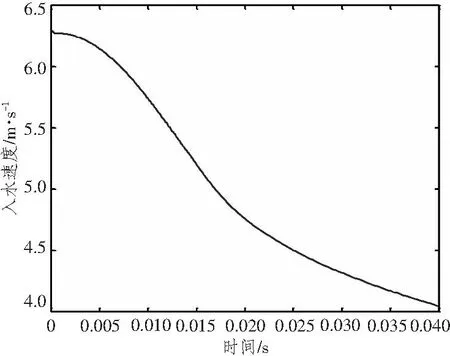
图16 二维模型中楔形体入水速度曲线Fig.16 Wedge speed of two-dimensional model during entry water
3楔形体入水角对砰击压力的影响
分别计算入水角为10°和15°的三维楔形体自由落体入水砰击压力,测量点位置同图1和图2,楔形体的长度、宽度、质量、初始入水速度与第1节中的入水角30°的楔形体相同。按照基础模型三建立有限元模型,细网格尺寸保持不变。图17为两楔形体入水过程中砰击压力极值,图18为相应的砰击压力系数。与图8中所示的压力分布有所不同,从P1到P5,该两楔形体的砰击压力极值依次逐渐增大,然后减小;砰击压力系数依次逐渐增大。由3个楔形体入水砰击计算结果可以看到,楔形体入水角会对砰击压力极值及压力系数分布产生很大的影响。当入水角较小时,砰击压力极值从中纵剖面到楔形体两侧依次逐渐增大,然后减小,砰击压力系数依次逐渐增大;当入水角较小时,砰击压力极值和压力系数均依次逐渐减小。这可能是由物体入水过程中水面隆起及射流现象引起的,物体入水过程中,射流会对物体底部产生猛烈冲击,而入水角越小,射流现象就越明显,入水角为10°时,射流较为明显,使得P2,P3点的砰击压力极值较大,随着楔形体入水速度的衰减,P4,P5处的砰击压力极值则随之减小;入水角为30°时,射流现象不太明显,又由于入水速度的衰减,导致砰击压力极值分布依次逐渐降低。
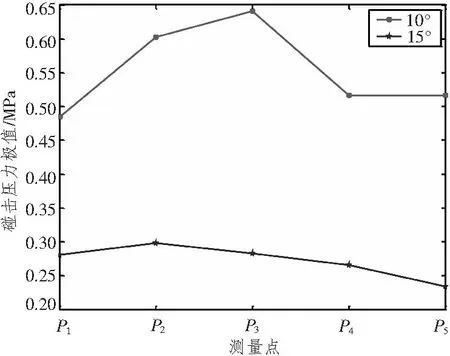
图17 砰击压力极值Fig.17 Extreme slamming pressure
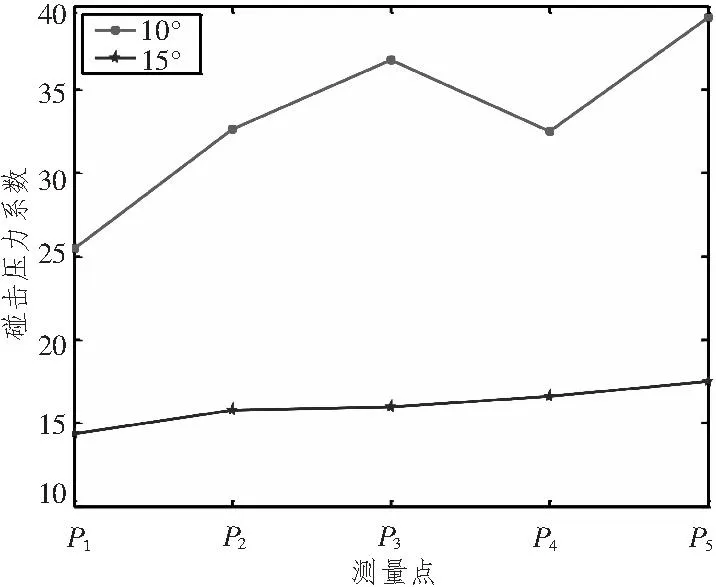
图18 砰击压力系数Fig.18 Slamming coefficient
4物体匀速入水砰击压力
分别计算三维楔形体和圆锥体匀速入水时各测量点产生的砰击压力,楔形体和圆锥体的入水角均为30°,同样以有限元模型三为基础计算模型,计算圆锥体砰击压力的有限元模型的细网格尺寸和模型三保持一致。通过调用Fluent的宏命令DEFINE_CG_MOTION使物体匀速入水。图19~图21分别为入水速度为4 m/s,6 m/s,8 m/s时各点的砰击压力极值。由计算结果可以看到,相同入水速度条件下,楔形体各点的砰击压力极值比圆锥体的大,但压力极值的分布趋势基本相同,从P1到P5都是先逐渐增大然后减小。
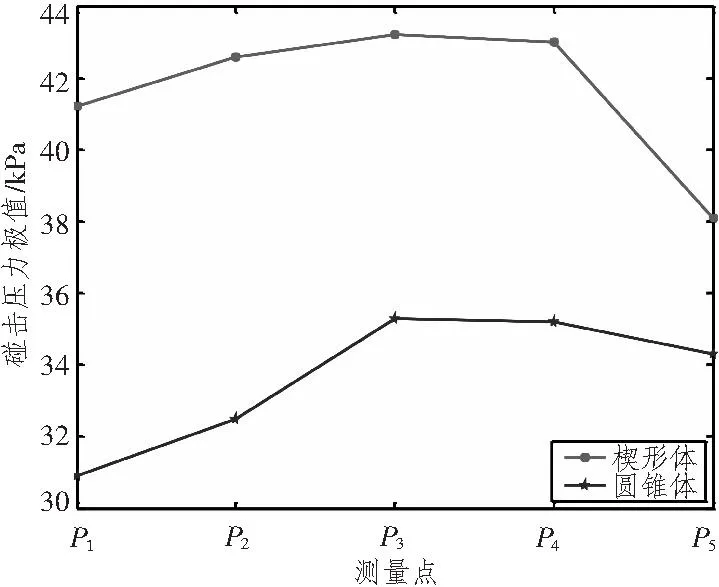
图19 入水速度为4 m/s砰击压力极值Fig.19 Extreme slamming pressure with speed 4 m/s

图20 入水速度为 6m/s砰击压力极值Fig.20 Extreme slamming pressure with speed 4 m/s

图21 入水速度为8 m/s砰击压力极值Fig.21 Extreme slamming pressure with speed 8 m/s
5结语
本文通过对三维楔形体和圆锥体的入水砰击压力进行计算,并将计算结果与试验结果进行比较,得出结论如下:
1)三维有限元模型中楔形体半宽与流域细网格的尺寸比在62.5∶1~175∶1之间范围内变化时,网格尺寸对砰击压力计算结果几乎没有什么影响。经过与试验结果的比较,本文选取模型三作为基础计算模型是合理的;
2)三维楔形体的长宽比对砰击压力有较大的影响,当长宽比大于3时,三维楔形体中横剖面的砰击压力计算可近似简化为具有同样剖面的二维楔形体入水问题;
3)楔形体入水角会对砰击压力极值及压力系数分布产生很大的影响。当入水角较小时,砰击压力极值从楔形体中纵剖面到两侧依次逐渐增大,然后减小;当入水角较小时,砰击压力极值依次逐渐减小。
4)相同入水速度条件下,三维楔形体的砰击压力比圆锥体的大,压力极值从P1到P5都是先逐渐增大然后减小。
参考文献:
[1]KARMAN V.The impact on seaplane floats during landing[R].NACA TN 321,oct.1929.
[2]WAGNER.Uber stass-und gleitvorgange undder oberflache von flussigkeiten[J].ZAMM,1932,12(4):193-215.
[3]CHUANG S L.Experiments on slamming of wedge-shaped bodies[J].Journal of Ship Research,1967,11(3):190-198.
[4]ZHAO R,FALTINSEN O M.Water entry of two-dimensional bodies[J].Journal of Fluid Mechanics,1993,246:593-612.
[5]OCHI M D,BONILLA N J.Pressure-velocity relationship in impact of a ship model dropped onto the water surface and in slamming in waves[R].AD-709071,1970,6.
[6]SCOLAN Y M,KOROBKIN A A.Three-dimensional theory of water impact.Part 1, Inverse Wagner problem[J].Journal of Fluid Mechanics,2001,440:293-326.
[7]顾懋祥, 程贯一, 张效慈.平头旋转壳撞水水弹性效应的研究[J].水动力研究与进展,1991(6):42-51.
[8]胡嘉骏,蔡新钢.船舶表面点砰击压力的预报方法[J].船舶力学,2005,9(1):63-70.
[9]陈震,肖熙.空气垫在平底结构入水砰击中作用的仿真分析[J].上海交通大学学报,2005,39(5):670-673.
[10]ZHAO R,FALTINSEN O,AARSNES J.Water entry of arbi-trary two-dimensional sections with and without flow separa-tion.Proc.21stSymp.on Naval Hydrodynamics, 1996.
The study of slamming pressure about three-dimensional wedge and cone
SI Hai-long,YU Hao,LI Zheng-jie,HU Jia-jun
(China Ship Scientific Research Center,Wuxi 214082,China)
Abstract:This paper calculates the slamming pressure of wedge and cone based on software of Fluent.The result agrees well with the experiment in term of the velocity of wedge during entry water and distribution of the slamming pressure.This paper mainly studies the effect of ratio on slamming pressure.The result indicates that the ratio have a great impact on slamming pressure.It could calculate slamming pressure of two-dimensional wedge instead of three-dimensional wedge which has the same middle section with the two-dimensional wedge when the ratio is higher than three.The wedge′s deadrise angle has a great impact on the distribution of extreme of slamming pressure.The slamming pressure of wedge is higher than those of cone when it entry water with the same speed.
Key words:velocity of entry water;slamming pressure;ratio
作者简介:司海龙(1984-),男,助理工程师,主要从事船舶砰击载荷研究。
收稿日期:2014-05-30; 修回日期: 2014-07-07
文章编号:1672-7649(2015)01-0017-06
doi:10.3404/j.issn.1672-7649.2015.01.004
中图分类号:U661.44
文献标识码:A
