非线性规划在机器人避障问题中的应用研究
2015-03-13张蓉
张 蓉
(天津工程职业技术学院,天津 300280)
非线性规划在机器人避障问题中的应用研究
张 蓉
(天津工程职业技术学院,天津 300280)
本文针对机器人避障的最短路径和最短时间路径问题建立优化模型,主要研究机器人行走过程中如何避开障碍物到达目标点的最短路径及最短时间路径。经分析可得,最短路径一定是由线和圆弧组成的。为方便计算,把较长的路径拆分为较简单的线圆结构图。依据这种方法,无论多复杂的路径图都可以拆分为这种相对简单的线圆结构来求解。对于最短路径问题,可通过穷举法找出可行路径,再用AutoCAD作出精确的路径图选出相对较短的路径,并利用Mathematic计算出路径长度,经计算可得机器人路障的最短路程。对于最短时间问题,由于转弯的半径和弧的圆心是未知的,路径是无法确定的,所以建立了非线性规划的优化模型,用LINGO软件求解得到。
最短路径;最短时间路径;避障问题;非线性规划;LINGO软件;Mathematic软件;AutoCAD制图;优化模型
1 引言
非线性规划是具有非线性约束条件或目标函数的数学规划,是运筹学的一个重要分支。非线性规划是20世纪50年代才开始形成的一门新兴学科。70年代又得到进一步的发展。非线性规划在工程、管理、经济、科研、军事等方面都有广泛的应用,为最优设计提供了有力的工具。
2 机器人避障问题
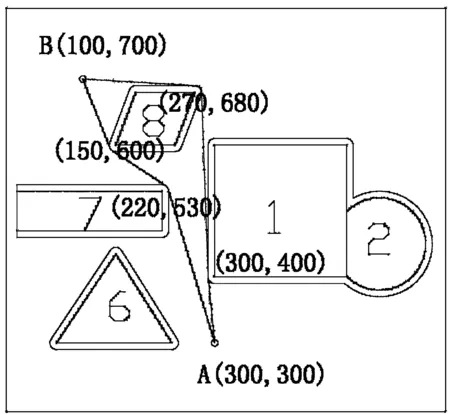
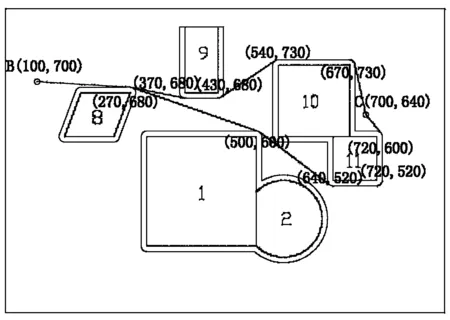
一个800×800的平面场景图如图1所示,在原点O(0, 0)点处有一个机器人,它只能在该平面场景范围内活动。图1中有12个不同形状的区域是机器人不能与之发生碰撞的障碍物,障碍物的数学描述如下表:
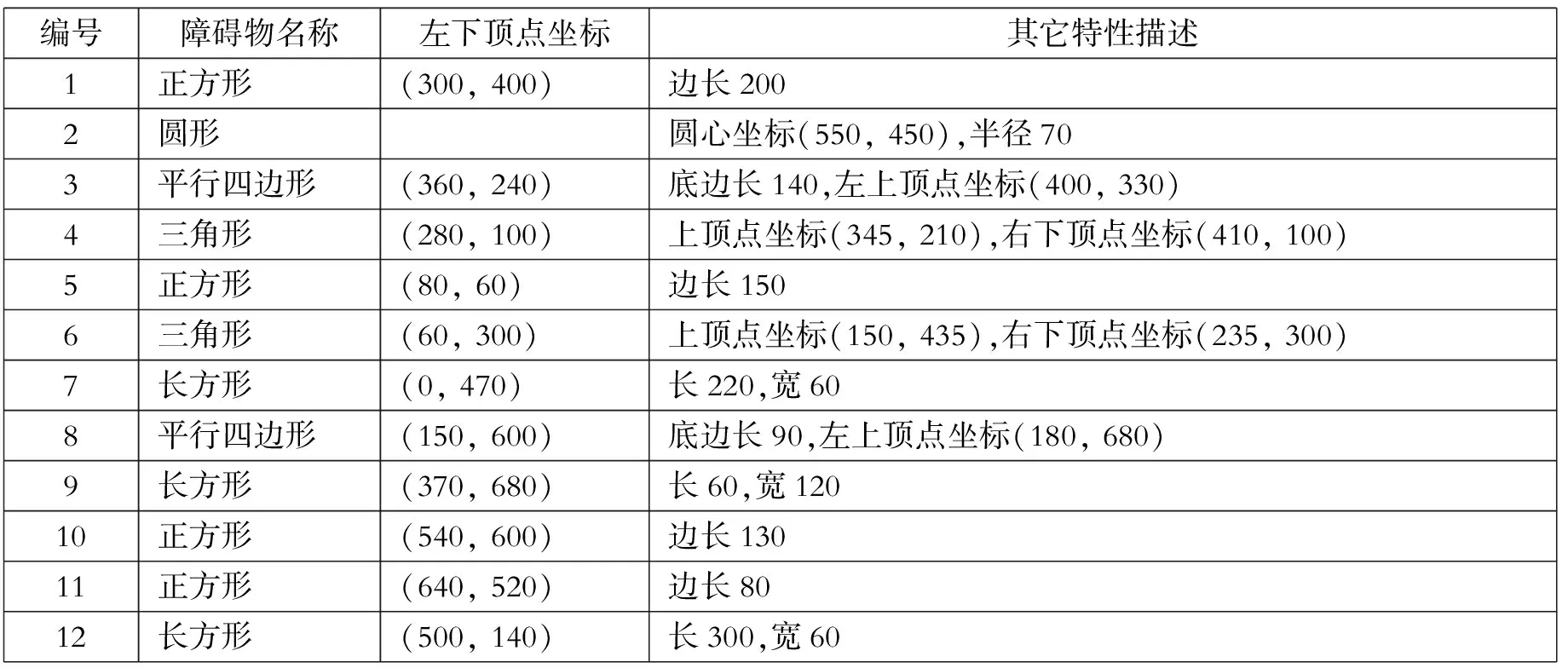
编号障碍物名称左下顶点坐标其它特性描述1正方形(300,400)边长2002圆形圆心坐标(550,450),半径703平行四边形(360,240)底边长140,左上顶点坐标(400,330)4三角形(280,100)上顶点坐标(345,210),右下顶点坐标(410,100)5正方形(80,60)边长1506三角形(60,300)上顶点坐标(150,435),右下顶点坐标(235,300)7长方形(0,470)长220,宽608平行四边形(150,600)底边长90,左上顶点坐标(180,680)9长方形(370,680)长60,宽12010正方形(540,600)边长13011正方形(640,520)边长8012长方形(500,140)长300,宽60
在图1的平面场景中,障碍物外指定一点为机器人要到达的目标点(要求目标点与障碍物的距离至少超过10个单位)。规定机器人的行走路径由直线段和圆弧组成,其中圆弧是机器人转弯路径。机器人不能折线转弯,转弯路径由与直线路径相切的一段圆弧组成,也可以由两个或多个相切的圆弧路径组成,但每个圆弧的半径最小为10个单位。为了不与障碍物发生碰撞,同时要求机器人行走线路与障碍物间的最近距离为10个单位,否则将发生碰撞,若碰撞发生,则机器人无法完成行走。
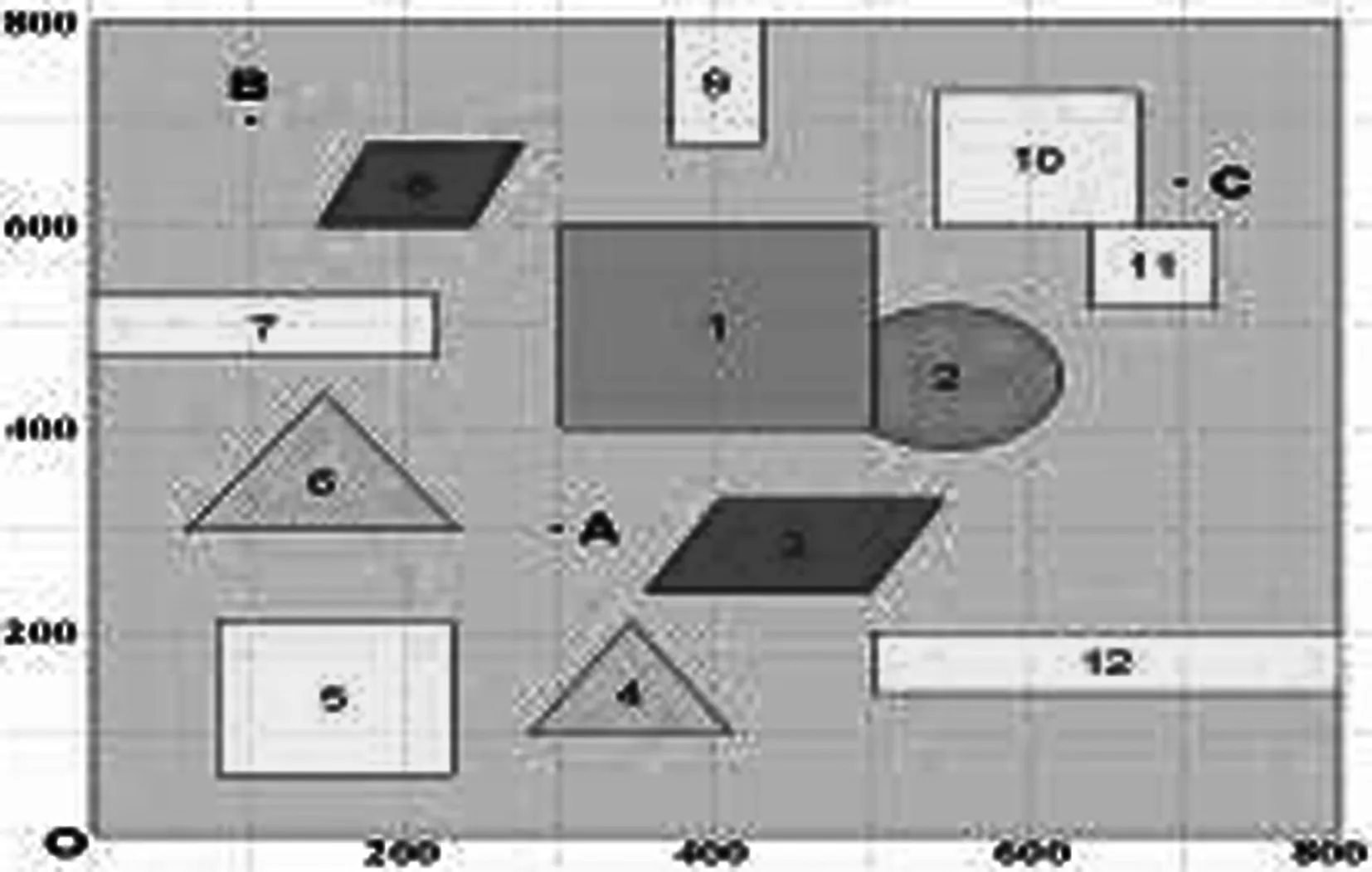
图1 800×800平面场景图
建立机器人从区域中一点到达另一点的避障最短路径和最短时间路径的数学模型。对场景图中4个点O(0, 0),A(300, 300),B(100, 700),C(700, 640),具体计算:
(1) 机器人从O(0, 0)出发,O→A、O→B、O→C和O→A→B→C→O的最短路径。
(2) 机器人从O(0, 0)出发,到达A的最短时间路径。
注:要给出路径中每段直线段或圆弧的起点和终点坐标、圆弧的圆心坐标以及机器人行走的总距离和总时间。
3 模型的建立
3.1 符号假设
在建立模型之前,先将模型建立在一下客观条件下:1.机器人在直线和圆弧中都能以各自的速度匀速行走,2.机器人在直线和圆弧之间连接时不停,3.除了指定障碍物外,机器人不受其他一切阻碍,4.机器人可以不停的走指定路程,5.障碍物是如题所说的完全的规则图形,6.人在行走过程中可以将它看为质点
文中涉及到的符号:(1)v:机器人直线行走的最大速度 (2)li:总路径的总长度 (3)v(ρ):机器人转弯时,最大转弯速度 (4)(xi,yi)、(mi,ni):表示图中点的坐标 (5)r:转弯半径
3.2 问题分析
(1)问题一中要求机器人从O点出发到达A、B、C及经过A、B、C回到O的最短路程。由于问题中障碍物太多,我们为了简化问题AutoCAD做出精确的机器人行走路线图,其中我们用直线及倒圆角把机器人不可去的地方用线画出来,从而直观的表示出机器人可以去的地方,然后我们便可以用切线把起点倒终点之间的无穷路线找出来,由于图中只提绝对精确的,所以通过比较可去掉明显路程较大的路程,然后在通过数值计算找出剩下路程中的最短路程。
(2)问题二中要求解从O到A的最短时间路径,转弯时圆弧的半径和圆心无法确定,切点的坐标无法确定。所以不能用第一问的穷举法,优化建模时只能用非线性规划。最后再用LINGO求解最优解。
3.3 模型分析
模型准备一:
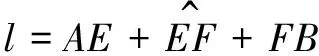
模型准备二:
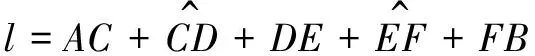
模型准备三:
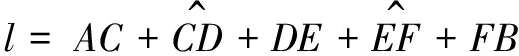
3.4 模型求解
3.4.1 问题一
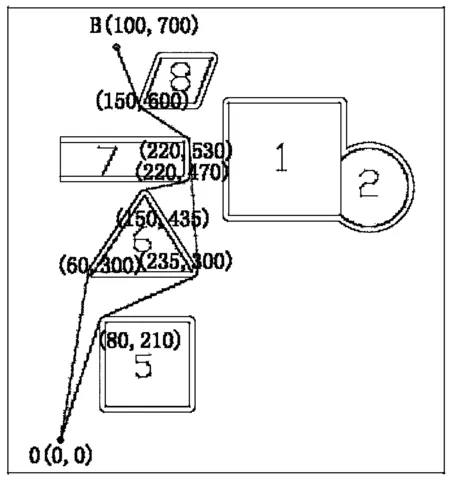
(1)O到A的最短路程图(如图四)
由图我们可以知道,从O到A的无数条路径中只有图中两条相对较短,其他路径的长度均大于图中两条。为了确定最短路线,我们对路线进行数值计算,由三个准备及mathematica计算,图中两条路线的总长度(l1表示障碍物5上边绿色线路图,l2表示障碍物下边绿色线路图)。
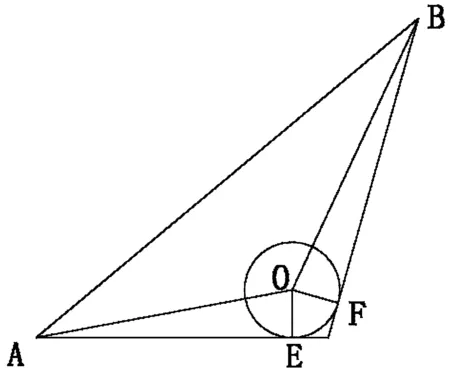
图一
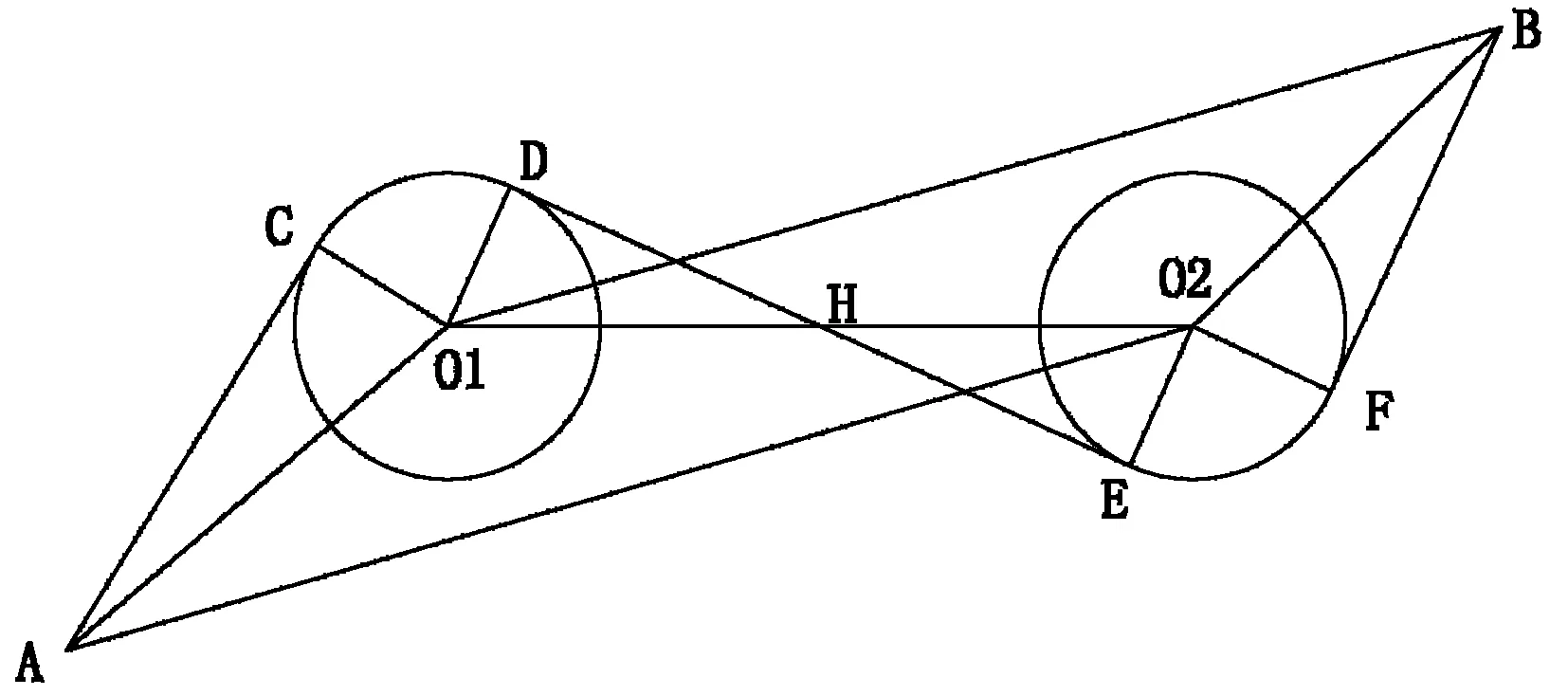
图二
图三
计算可得:l1=471.073 ,l2=498.426
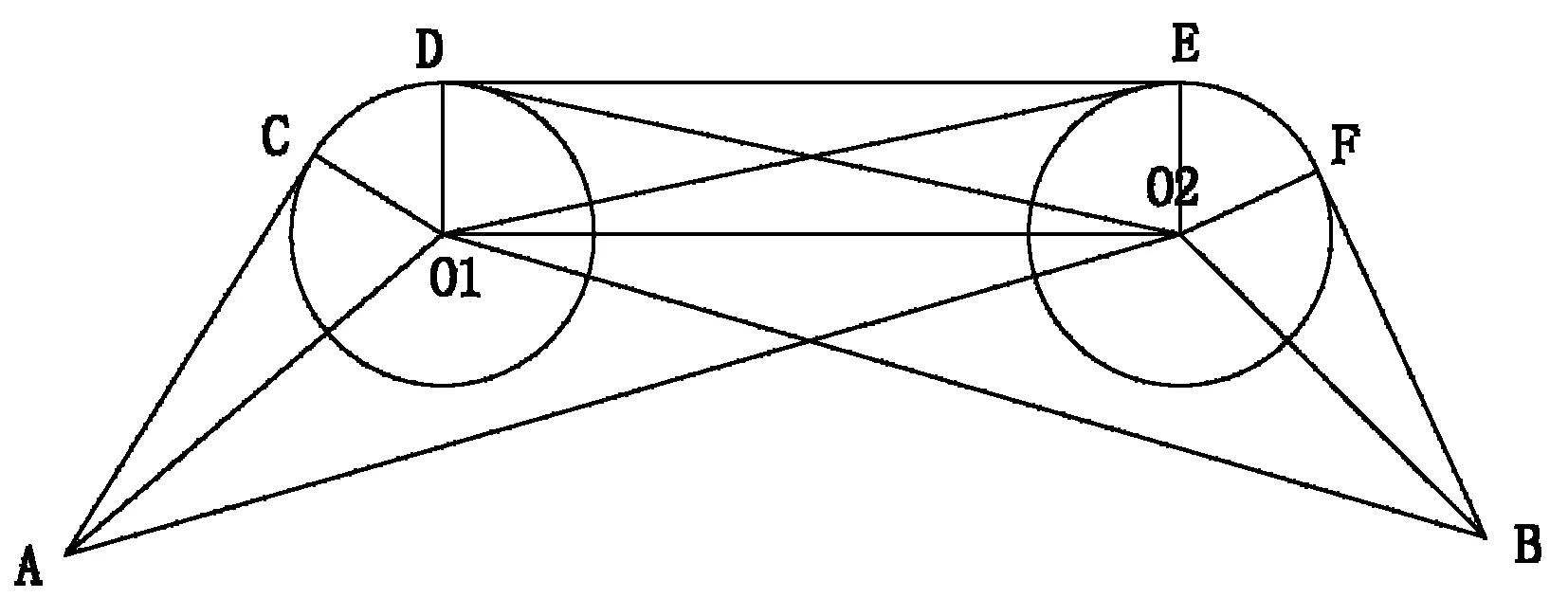
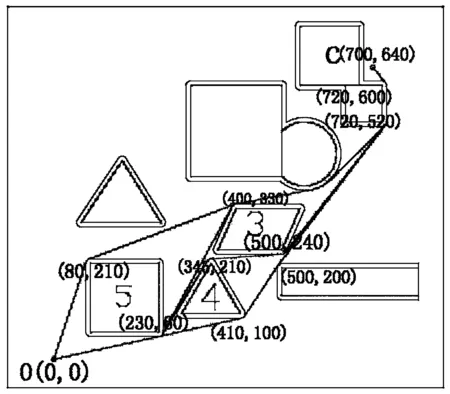
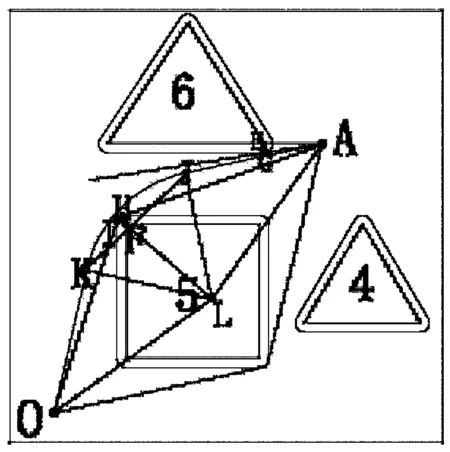
由于l1 (2)O到B的最短路程图(如图五) 由图我们可以知道,从O到B的无数条路程中只有图中两条相对较短,其他路程的长度大于图中两条路程的长。为了确定最短路线,我们对路线进行数值计算,由三个准备及mathematica计算图中两条路线的总长度(l3表示障碍物6左边绿色线路图,l4表示障碍物6右边绿色线路图)。 图四 图五 计算可得:l3=891.113,l4=913.563 由于l3 (3)O到C的最短路程图(如图六) 由图我们可以知道,从O到C的无数条路程中只有图中四条相对较短,其他路程的长度均大于图中四条路程的长。在l5和l6之间的两条路径由于转弯太多长度明显大于l5和l6两条路径的长,所以只计算l5和l6两条路径的长。为了确定l5和l6两条路径的最短路线,利用LINGO软件进行数值计算、三个准备及mathematic软件计算图中两条路线的总长度(l5表示障碍物5上边绿色线路图,l6表示障碍物5下边绿色线路图)。 计算可得:l5=1947.378,l6=1091.537 由于l5>l6,所以l6即下边绿色线路图最短,它的切点坐标从左到右依次为:(232.115,50.2262)、(232.169,50.2381)、(403.644,107.72)、(407.831,109.762)、(491.655,205.51)、(492.062,206.082)(727.938,513.918)、(730,520)、(730,600)、(727.718,606.359)圆心坐标(230,60)、(410,100)、(500,200)、(720,520)、(720,600) (4)A到B的最短路程图(如图七) 由图我们可以知道,从O到B的无数条路程中只有图中两条相对较短,其他路程的长度大于图中两条路程的长,于是求解图中两条路径的长。 图六 图七 为了确定最短路线,我们对路线进行数值计算,由三个准备及mathematic计算图中两条路线的总长度(l7表示障碍物8左边绿色线路图,l8表示障碍物8右边绿色线路图)l7=562.635,l8=568.815 由于l7 (5)B到C的最短路程图(如图八) 由图我们可以知道,从B到C的无数条路径中只有图中两条相对较短,其他路径的长度大于图中两条路径的长,于是求解图中两条路径的长。经分析可得,障碍物10下的路径由于转弯太多所以舍去。则确定l9为最短路线,我们对路线进行数值计算,由三个准备及mathematic计算图中l1路径的总长度(l9为障碍物10上边的路径)。 计算可得:l9=839.735 它的切点坐标从左到右依次为:(270.586,689.983)、(272,689.798)、(272,670.202)、(370,670)、(430,670)、(435.588,671.707)、(534.412,738.293)、(540,740)、(670,740)、(679.767,732.145)圆心坐标为(720,680)、(370,680)、(430,680)、(540,730)、(670,730) (6)由以上问题可以得出从O→A→B→C→O的最短路径为L=l1+l6+l7+l9=2964.944 3.4.2 问题二 从O到A的最短时间路径图(如图九) 图八 图九 机器人从O经过弧KF到A的示意图,设O、A、F、G、I、J、K、L、E、H的坐标为(x1,y1),(x2,y2)(x3,y3)(x4,y4)(x5,y5)(x6,y6)(x7,y7)(x8,y8)(x9,y9)(x10,y10)直线AG、AJ、DI、DK、AH,斜率K1、K2、K3、K4、K5圆心角θ,半径为R0,弧长为l. 模型的建立 (x6-x8)2+(y6-y8)2+(x2-x6)2+(y2-y6)2=(x2-x8)2+(y2-y8)2 (x1-x8)2+(y1-y8)2=(x1-x7)2+(y1-y7)2+(x7-x8)2+(y7-y8)2 (x2-x3)2+(y2-y3)2=(x2-x10)2+(y2-y10)2+102,102=(x3-x10)2+(y3-y10)2 102+(x4-x2)2+(y4-y2)2=(x2-x9)2+(y2-y9)2,102=(x4-x9)2+(y4-y9)2 y8-y7>0.1,x7-x8>0.1,300-x8>1,x8-x6>0.01,x1=0、y1=0、x2=300、y2=300、x3=80、y3=210、x9=235、y9=300 (x6-x8)2+(y6-y8)2+(x2-x6)2+(y2-y6)2=(x2-x8)2+(y2-y8)2 (x1-x8)2+(y1-y8)2=(x1-x7)2+(y1-y7)2+(x7-x8)2+(y7-y8)2 (x2-x3)2+(y2-y3)2=(x2-x10)2+(y2-y10)2+102,102=(x3-x10)2+(y3-y10)2 102+(x4-x2)2+(y4-y2)2=(x2-x9)2+(y2-y9)2,102=(x4-x9)2+(y4-y9)2 x8-x7>0.1,x8-x6>0.1,y8-y6<0.1,y6-220>1,y8-y7>0.1,x7-x8>0.1,300-x8>1 x8-x6>0.01,x1=0、y1=0、x2=300、y2=300、x3=230、y3=60、x9=280、y9=100 通过LINGO计算可得出最少时间为t=109.714s 本文建立模型时采用LINGO软件编程、mathematic软件和CAD制图,可信度较高,实用性较强,路线图精确清晰,给建模求解带来了方便,其中效率有待进一步改进,以适用障碍物多模型的建立。 该模型简单明了,思路清晰,容易理解,可以灵活应用,具有很强的使用价值,因此该模型推广到运输网络中、避障救援项目、舰船通道路线设计中、城市道路建设、物资供应站选址等也有很重要的作用,分析和研究最短路问题趋于热门化。 [1]胡运权,郭耀煌.运筹学教程[M].北京:清华大学出版社,2007. [2]谢金星,薛毅.优化建模与LINDO/LINGO软件[M].北京:清华大学出版社,2005. The Research of the Application of Nonlinear Programming in the Obstacle Avoidance of Robots ZHANG Rong (TianjinEngineeringVocationalandTechnicalCollege,Tianjin, 300280) This paper mainly aimed to find the shortest path and the shortest time path when robots tried to avoid the obstacles to get to the target point and to establish an optimization model for these two paths. The analysis showed that the shortest path must always be composed with lines and arcs. For convenience, we split the longer path into relatively simple line round structures and no matter how complex the path graphs are, all of them can be solved by this method. For the shortest path, we can find the viable path by the method of exhaustion and then use AutoCAD software to make a precise path graph in order to select a relatively shorter one, the length of it can be calculated by use of Mathematic software and that is the shortest path of obstacle avoidance of robots. For the shortest time path, due to the unknown radius of the turning and center of the arc, it can not be determined, so we can establish an optimization model for the nonlinear programming to get it by use of LINGO software. shortest path;the shortest time path; obstacle avoidance; nonlinear programming; LINGO software; Mathematic software; AutoCAD drawing; optimization model 2014-07-07 张蓉(1980-),女,汉族,天津工程职业技术学院讲师,从事数学及计算机教学与研究工作。 TP242 A 1673-582X(2015)02-0047-06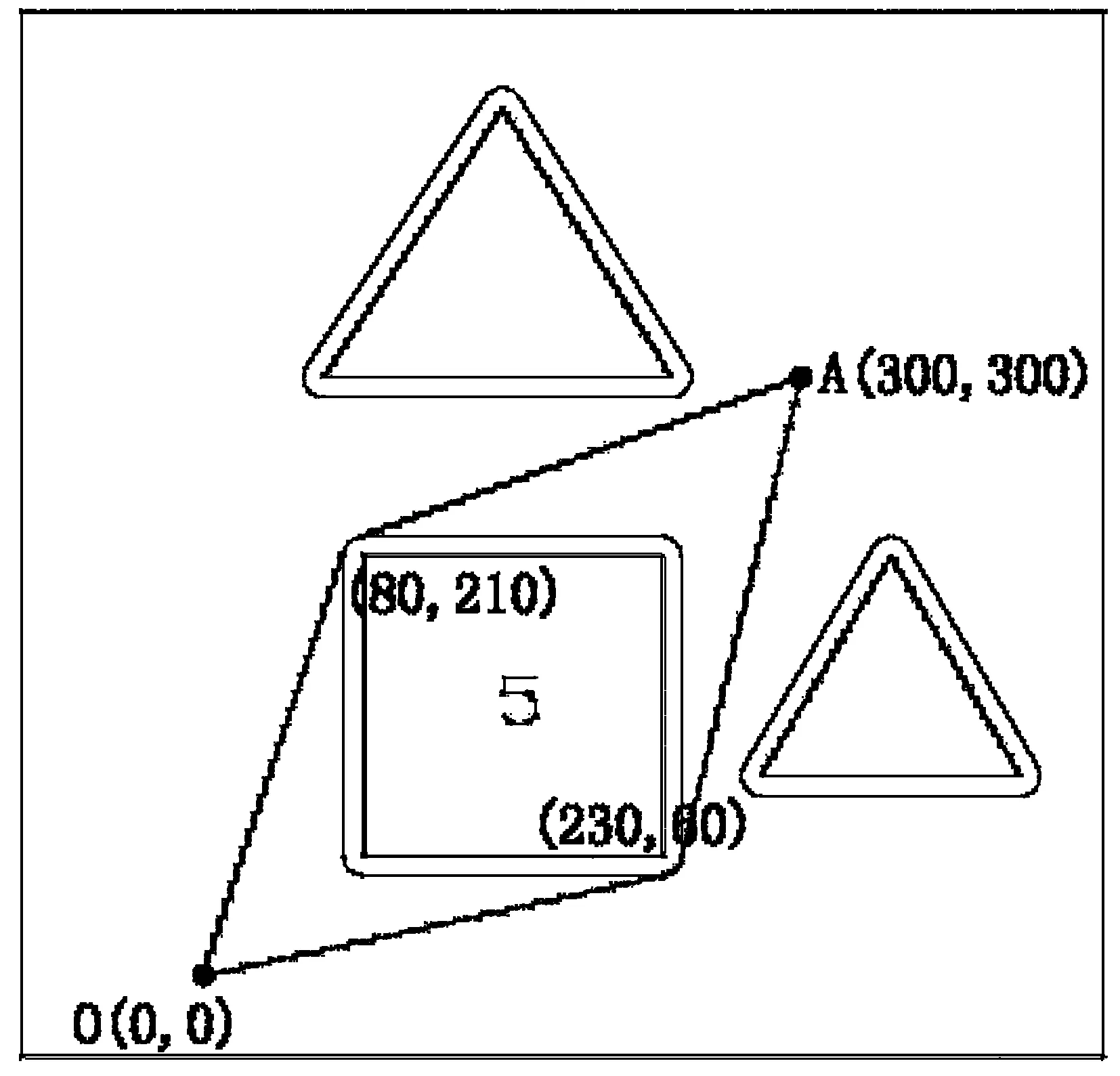
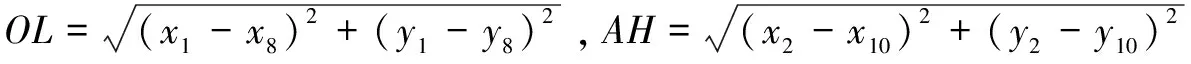
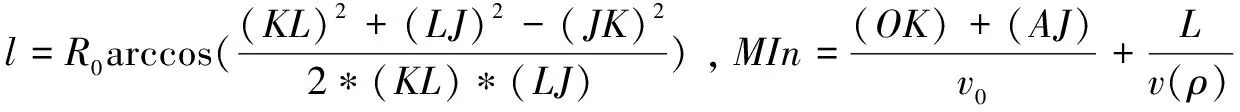
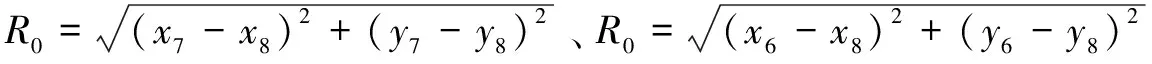
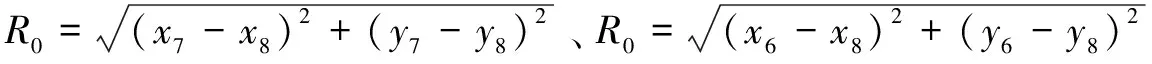
4 模型的评价改进及推广
