具有模糊交货期并赋有延迟惩罚的平行机排序问题

叶彩虹

(重庆师范大学数学学院,重庆 401331)

具有模糊交货期并赋有延迟惩罚的平行机排序问题

叶彩虹

(重庆师范大学数学学院,重庆 401331)

考虑具有模糊交货期并赋有延迟惩罚的平行机排序问题,讨论了赋有延迟惩罚的排序问题和总误工问题,模型中利用三角形模糊数把交货期表示出来,工件具有准备时间,并且工件允许中断,目标是有一最优序列能够得到最大延误惩罚,用满意度来讨论总误工时间,并且得到最优排序以便最小化总误工时间,对这些问题,给出算法.

排序;模糊交货期;三角形模糊数;准备时间;满意度

排序问题是组合优化中一个极为重要的课题,而往往在现实的加工过程中,由于有许多的不确定因素,很难事先确定工件的加工时间和工期,因此研究不确定环境下的生产调度问题有着重要的意义.事实上,早在1979年,Prade[1]就将模糊集的理论用于生产调度问题的研究;霍录景和米洪海[2]利用三角形模糊数考虑了平行机具有模糊交货期的最大延误问题,并给出算法和一些定理;袁芬和谷云东[3]等人讨论了平行机具有模糊交货期的一些性质和一些比较好的结果.目标是最小化满意度,而满意度就是最大限度的生产调度,并给出满意度的一些定理和最优的算法;Fardin[4]利用另外形式的三角形模糊数讨论了具有模糊加工时间的最大完工时间,给出了模糊工期的隶属函数,并给出了模糊工期的一些定义与性质;Wang[5]讨论了单机并具有到达时间的且工期是模糊的一系列问题.

本文考虑平行机具有模糊交货期下的最大延迟惩罚,并讨论关于在最优调度下的总误工时间,给出一些基本性质和算法.为此,引入三角形模糊数运算如下:

定义1[2]两个三角形模糊数相等的充要条件是a1=b1,a2= b2,a3=b3.

定义2[2]有两个三角形模糊数(TFNS),则的模糊和为

定义3 若k≥0,k·(a,b,c)=(ka,kb,kc)为三角形模糊数的数量乘法.

1 最小化延迟惩罚问题

用三角形模糊数来表示模糊交货期.给出经典数和模糊数相减的方法,经典数和模糊数相乘的方法,如何比较模糊数的大小,本节研究以下两个问题:

1.1 问题描述

设有工件集J={J1,J2,...,Jn},工件的加工时间、交货期和完工时间分别为pi,和Ci(1≤i≤n),机器的数量为2.假设工件的准备时间为rj,并假定:

(1)工件具有不同的准备时间;

(2)工件加工允许中断;

(3)一台机器不能同时加工两个工件;

(4)机器加工过程中允许出现空闲;

(5)一个工件不能同时在两台机器上加工;

(6)工件的交货期是模糊数.

定义4[4]误工任务为Tj,其交货期用三角形模糊数(TFNs)表示为=(d1j,d2j,d3j),其中d1j代表最优值,d2j代表最合理值,d3j代表最差值.

定义5 d1j≤d2j≤d3j,为模糊延误值,称为模糊延误惩罚值.

定义6 对于误工任务为最大模糊延误惩罚值.

1.2 最大延误惩罚

对于每个任务Tj∈T都给定了加工时间pj,准备时间rj和交货期,用三角形模糊数=(d1j,d2j,d3j)来表示模糊交货期.pj≥0,rj≥0且Cj≥0,则的隶属函数可以表示为:

t是实数.若t=Cj则(Cj)表示完工时间Cj和模糊交货期之间的关系.取0≤λ≤1,如果(Cj)＜λ ,则称Tj为误工任务,得到下面判断任务是否误工的判断法则:

对于Uj=1的任务Tj,计算,在计算的时候,需要比较的大小.

本文采用文献[5]提出的三条准则比较两个模糊数的大小.对于两个三角形模糊数(TFNS)=(a1,a2,a3),=(b1,b2,b3),

准则1[5]:若

准则2[5]:如果(3)中不能够比较并排序,若

准则3[5]:如果(3)(4)都不能够排序两个模糊三角数,若a3-a1＜b3-b1,则＜.

这里的EFDD序不一定给出这个问题的最优排序.因此考虑一种特殊情况:每个工件的权重和模糊交货期满足一致性假设,即对于工件Ji和Jj有wi≤wj⇔di≤dj.此时研究问题有以下性质.

引理1 对于当前问题,如果每个工件的权重与交货期一致,则存在一个最优序列,使得每个工件都按照交货期的EFDD序排列.

证由于每个工件的权重和交货期一致,所以每个工件的ERD序与EFDD序是一样的,对于工件可以采用二交换法证明,设π1按照ERD和EFDD序排列的一个最优序列,考虑其中的任意两个工件i和j,并且给出≤,则wi≤wj.假设这两个工件的开始时间和完工时间是两个区间t[1,t1+x]和t[2,t2+x],并且t2＞t1+x,因此i有一个加工过程在t[1,t1+x]区间,并且间隔一段距离后,j在t[2,t2+x]区间上加工,i的到达时间为t1,j的到达时间为t2,并且Max{ri,rj}≤t1,工件i与工件j交换位置获得最新序列π2.

max{Ci(π2),Cj(π2)}-max{Ci(π1),Cj(π1)}=0,Cj(π1)=t2+x,Cj(π2)=t1+x,所以Cj(π2)≤Cj(π1).

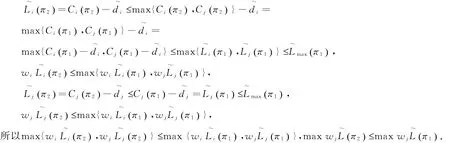
定理1 问题p 2|rj,prem|max wj能够在O(n2)时间内得到解决.

《导基》的智慧课堂教学根据全国导游资格考试大纲与题型，对课程内容进行合理的智慧构建，采用课件讲解、图片、视频、问题、讨论、头脑风暴、投屏演示、现场练习等多种手段强化教学内容，加深学生们对知识点的归纳、辨析与理解，强化对知识点的记忆与灵活运用，减少测评时出错，提高考证通过率。

证算法的计算量主要体现在第一步和第二步上,对工件的到达时间有先到先排的时候有一个序列,需要时间为O(n log n),由于在此基础上还需要对工期进行排列,需要在O(n log n)时间内解决,所以总的计算量为O(n2).

引理2 两个分别拥有元素xj和yj且个数相等的序列,如果这两个序列按相反的单调顺序排列,那么对应元素的乘积和最小.

2 总延迟惩罚

考虑平行机中的总延迟惩罚的问题,给出类似算法.

定理2 工件按照ERD序排列,并且交货期是按照EFDD序排列,得到一个最优排序,能够求出延误修正值,然后再根据准则1,2,3进行比较得到从小到大排序,并且让权重按照w1≥w2≥...≥wn,能够得到最优序列使目标有最优值.

证有引理2可知,利用二交换法能够求出延误工件的延误修正值,并把得出的序列和权重按照相反的单调顺序能够得到最优解

算法1

步骤1 当前到达工件中按照先到先排,若只有一个工件到达时,让其在任意空闲的机器上加工;若有两个工件到达,让其在两台机器上加工;若有多个任务到达,应用准则1,2,3对模糊工期进行排序,选出模糊交货期小的两个工件在p1和p2上加工.若两个工件的模糊交货期相等,则按照权重的w1≥w2≥...≥wn排列.

步骤2 当某个工件加工完毕后,在已经到达的工件中应用准则1、准则2和准则3对模糊交货期进行排序,按照的序列在空闲机器上加工.若模糊交货期相等,则按照权重的w1≥w2≥...≥ wn排列.

步骤3 若又有新工件到达时,转步骤1;若所有工件都已经到达,转步骤4.

步骤4 所有的工件都已到达,对所有未加工的工件和未加工完的工件应用准则1、准则2和准则3按照模糊交货期不减的顺序制表,取表最前的两个工件在两台机器上加工,若有多个工期相等并最小,则按照wj不增的顺序,选取两个最前的加工.

3 最小化总误工问题

在上述基础上,给出算法并算出最小的总延误模糊修正时间.工件集合J={J1,J2,...,Jn},在模糊调度中,模糊工期反映了决策者对工件的完工时间的满意度是逐渐变化的,作为经典调度问题的推广,在模糊调度中可以定义完工期限和误工区域以及可行调度的概念.

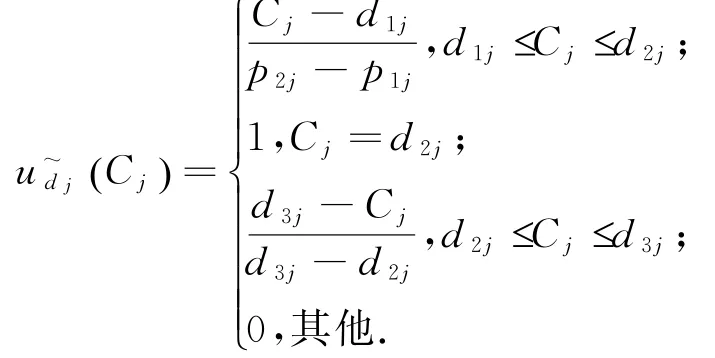
性质1 如果有λ＞0,则对问题的任何一个最优调度π*,①工件Jj不误工的完工时间满足;

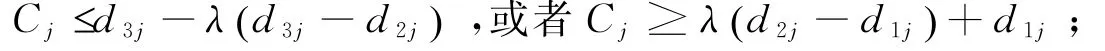
②工件Jj误工的完工时间满足;

证①因为λ＞0,在隶属函数中就满足;

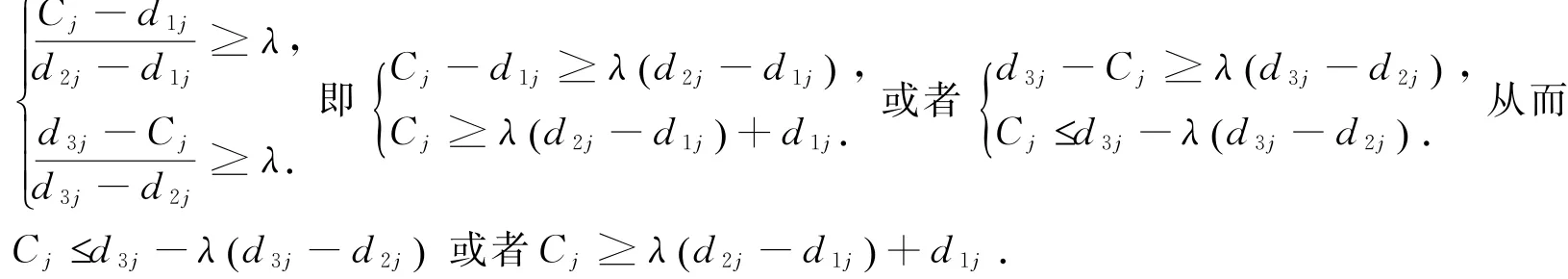
②类似可证明.

性质2 若(Cj)=0,则有Cj≥d3j或Cj≤d1j,若是Cj≥d3j,则全部工件都误工,总误工会越大,若Cj≤d1j,则没有误工工件,

证由题意可得,若Cj≥d3j,并且知道d1j≤d2j≤d3j,则有完工时间大于最大工期,所以通过判断法则,所有的工件都误工.若Cj≤d1j,则有工件完工时间小于最小工期,则所有工件都不误工,并且0.

定义7[4]对给定的满意度λ(0≤λ≤1),称:Dj1(λ)=d3j-λ(d3j-d2j),或者有Dj2(λ)= λ(d2j-d1j)+d1j为工件Jj对应于满意度λ的误工区域.即Cj≤Dj2或者Cj≥Dj1都让工件误工.

性质3 如果对任何λ(0＜λ＜1),Cj≤D2或者Cj≥D1都不成立,则此时对工件集按照EFDD序排列能够得到最优序.

基于以上的分析,给出一算法解决本节的问题:

算法2

步骤1 工件Jj先到的先排,λ(λ≠0)值固定.若d1j≤pj≤d2j,工件集(J1,J2,...,Jn)按照Dj2= λ(d2j-d1j)+d1j的非减的次序依次排在p1和p2机器上.若d2j≤pj≤d3j,则Dj1(λ)=d3jλ(d3j-d2j)的非增序列依次排在p1和p2机器上.

步骤2 当λ=0;工件集按照先到先排,并利用准则1、准则2、准则3来比较模糊工期的大小,并按照工期小的先排,算出∑jTj.

4 结束语

本文讨论了平行机具有模糊工期的最大延迟惩罚和总误工的一些相关问题,目标是怎样排序能够使最大延迟惩罚最小,并且也讨论了使总误工最优的排序.对其他模型的讨论和其他机器环境下的排序问题有待进一步的研究.

[1]Prade H.Using Fuzzy Set Theory in a Scheduling problem:A Case Study[J].Fuzzy Sets and Systems,1979,2(2):153-165.

[2]霍录景,米洪海.具有模糊交货期的平行机排序问题[J].科学技术与工程,2010,10(29):7223-7225.

[3]袁芬,谷云东,尘非.关于模糊工期平行机调度问题的若干结果[J].北京师范大学学报,2006,42(3):232-235.

[4]Fardin Ahmadizar,Leila Hosseini.Minimizing makespan in a single-machine scheduling problem with a learning effect and Fuzzy processing times[J].Int J Adv Manuf Technol,2013,65:581-587.

[5]Wang C,Wang D,Ip WH,et al.The single machine ready time scheduling problem with fuzzy processing times[J].Fuzzy Set Systems,2002,127:117-129.

[6]刘春来,赵传立.工期窗口安排与具有退化效应和维修活动的单机排序[J].数学实践与认识,2012,42(11):122-130.

[7]吴会江.一种具有模糊交货期的单机调度问题[J].科学技术与工程,2005,5(9):592-593.

[8]Fardin Ahmadizar,Leila Hosseini.Single machine scheduling with a position-based learning effect and fuzzy processing times[J].Int J Adv Manuf Technol,2011,56:693-698.

[9]Ahmadizar F,Ghazanfari M,Fatemi Ghomi SMT.Application of chance-constrained programming for stochastic group shop scheduling problem[J].Int J Adv Manuf Technol,2009,142:321-334.

[10]Orcun S,Altinel IK,Hortascu O.scheduling of batch processes with operational uncertainties[J].Compution Chem Eng,1996,20:S1191-S1196.

[11]Liu B,Liu YK.Expected value of fuzzy variable and fuzzy expected value models[J].IESS Trans Fuzzy Systems,2002,10:445-450.

With fuzzy due dates penalties and parallel machine scheduling problems

YE Caihong

(College of Mathematics,Chongqing Normal University,Chongqing 401331,China)

Consider having a parallel machine scheduling problem with fuzzy due dates,discussed the scheduling problem with due dates and total tardiness problem,using the triangle in the model of fuzzy number to the due date that come out,and have time to prepare,and the work piece is allowed to interrupt,the goal is to have an optimal sequence to get the maximum tardiness penalty,with satisfaction to discuss the total tardiness,and obtain the optimal scheduling to minimize the total tardiness,to these problems the algorithm.

scheduling;fuzzy lead time;triangle fuzzy number;preparation time;satisfaction

O223;C93

:A

:1671-9476(2015)05-0009-0005

10.13450/j.cnki j.zknu.2015.05.003

2014-11-20;

:2015-03-30

国家自然科学基金(No.61302180);中国博士后基金面上资助项目(No.2013M540698);重庆市科委自然科学基金(No.cstc2014jcyj A0003);重庆市教委自然科学基金(No.KJ130606);重庆师范大学重点项目(No.2011XLZ05)

叶彩虹(1990-),女,四川达州人,硕士研究生,研究方向:排序论.