美式期权定价的一种蒙特卡洛方法
2015-03-13张丽虹
张丽虹
(云南财经大学马克思主义学院,昆明 650221)
引言
在最近的几十年里,金融衍生市场的发展已经成为影响经济的重要现象,衍生市场是相对于基础市场而言的。金融衍生物是一种风险管理工具,它的价值依赖于基本的原生资产(或称标的资产)的价格变化。在金融市场,商品市场有很多形式的金融衍生工具,其中远期合约、期货和期权是三种最基本的金融衍生工具。如果把原生资产设定为股票、债券、汇率或商品等,那么为了对这些原生资产进行风险管理,相应的有:股票期货(期权)、债券期货(期权)、货币期货(期权)以及商品期货(期权)等[3,7]。
在市场经济发达的国家,期权市场已是构成其证券市场的一个重要组成部分。近二十年来,国际金融界对期权理论的研究和应用投入了巨大的关注。特别是在西方发达国家,期权理论的发展日新月异,期权应用研究也紧随其后[3,7]。从金融期权研究得出的原理、方法和结论不仅仅应用于期权投资领域,还可以广泛应用于宏观、微观经济和管理问题的分析与决策[8]。瑞典皇家科学院将1997年度的诺贝尔经济学奖授予两位对现代期权理论研究有突出贡献的经济学家:美国斯坦福大学教授梅隆·舒尔斯(Myron Scholes)和哈佛大学教授罗伯特·莫(Robert C.Merton),这表明全世界对期权理论研究和实际应用重要性的认可[5,7]。由于历史、体制、学科建设等方面因素的影响制约,期权理论在我国的研究才刚刚开始,其应用也几乎呈空白状态。但我国政府、金融学术界和实务界已经越来越重视这一理论的研究和应用。国务院曾多次指示要加快金融科学的设立,国家自然科学基金会对金融数学、金融工程的研究项目支持力度也较大。现在已有相当一部分学者正活跃在这一领域,许多大学相继成立了金融数学系和金融工程中心,并开始了相应的学术研究和人才培养工作,这将对中国的金融改革,特别是金融数学、金融工程的发展做出有益的尝试和贡献。期权理论作为金融数学的一个重要研究内容也将得到迅速的发展。随着中国经济市场化进程的发展和各方面条件的成熟,期权市场在中国的发育和发展是中国市场体系,特别是金融市场发展与完善过程中的一项重要内容,是大势所趋[1]。
期权是最重要的金融衍生工具之一,合理定价则是期权发挥其功能的基础。对于欧式期权,已经有了经典的Black-Scholes公式,但由于美式期权具有可提前执行的特性,Black-Scholes公式并不适用[7]。
期权作为一种衍生金融产品,它的价格决定于标的资产价格的变化。标的资产的价格变化是不确定以及随机的,所以由此产生的期权价格变化也是随机的。但是一旦标的资产的价格确定下来,那么作为其衍生物的期权的价格也将随之确定,即存在函数Vt=V(St,t)。它表示若在t时刻原生资产的价格为 St,则期权的价格为 Vt=V(St,t)。这里的期权价格V(St,t)是一个确定的二元函数。通常在期权的到期日那天,期权的价值(或成为期权的收益、期权的价格)V(St,t)是确定的。但是期权生效日t=0那天的期权价格即期权金是未知的。因为他是期权购买者为了取得这个未定权益所要付出的代价。我们的计算目的就是求出期权金的值[1]。
通常计算美式期权的方法有有限差分法、二叉树法及蒙特卡洛法[2,6,9]。本文将讨论如何利用蒙特卡洛方法来计算美式期权的价格。国内学者在考虑美式期权定价问题的蒙特卡洛方法时,比较少详细讨论方法的具体设计过程[6,9-12],并且由于美式期权一般不具有封闭解,所以人们通常依靠数值解法来解决这一问题。本文将详细讨论方法的设计过程,并用Matlab程序在计算机上数值实现该过程。本文将按照下面的方式来组织:(1)简单介绍美式期权的定义、美式期权的特性及分类等基本概念,帮助人们更好地理解美式期权;(2)详细讨论美式期权定价的蒙特卡洛方法设计与数值计算过程;(3)得出计算结果并与传统的有限差分法计算得到的结果相比较。
一、美式期权的基本概念
美式期权是指可以在成交后有效期内任何一天被执行的期权。也就是指期权持有者可以在期权到期日以前的任何一个工作日,选择执行或不执行期权合约。它通常分为美式看涨期权与美式看跌期权。
美式看涨期权在行权期内,如果标的资产S高于敲定价格K,则持有者随时可以以敲定价格K买进标的资产。此时持有者以价格K买入标的资产,在市场中又可以以即时价格S卖出,获得利润S-K;若在行权期内,标的资产的价格始终低于敲定价格K,则持有者可以选择不买进任何标的资产,此时获得的利润为0,所以看涨期权的最终价格是确定的:V(S,t)=max(S-K;0)。
美式看跌期权在行权期内,如果标的资产价格S低于敲定价格K,则持有者随时可以以敲定价格K卖出标的资产,获得利润K-S;若在行权期内,标的资产的价格始终高于敲定价格K,则持有者可以选择不卖出任何标的资产,此时获得的利润为0,所以看跌期权的最终价格是确定的:V(S,t)=max(K-S;0)。
二、美式期权定价的蒙特卡洛方法
首先假定美式期权标的资产的价格,也就是S=S(t)服从下面的随机过程:



对于任意的t>0都成立,这里z是服从标准正态分布随机变量(均值0,方差1)。在下面的蒙特卡洛方法计算中,我们就是利用公式(1)来模拟标的资产在任意t时刻的价格。
下面讨论蒙特卡洛方法计算在t=0时刻美式期权的价格。设t=T是美式期权交割日时间,t=0是美式期权开始生效的那一时刻,S(t)表示美式期权标的资产在t时刻的价格。假定 t0,t1,t2,…,tm满足:
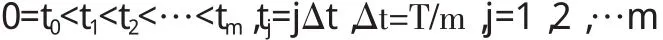
且记Si=S(ti),i=0,1,2,…,m;这里的m是一个给定的正整数。同时假定美式期权只可能在t1,t2,…,tm这m个有限时刻行权。下面,可以记Vi(s)表示在t=ti时刻且标的资产的价格Si=s时美式期权的价格。并且记hi(s)=h(Si=s),这里规定:

如果r(t)是一个常函数,例如r(t)=r不变,则Di-1,i=e-r(ti-ti-1),若进一步规定 ti=iΔt,i=0,1,2,…m则:

本文首要的计算目的是求出V0(s)的值,也即在t=0时刻且标的资产价格S0=s时美式期权的价格。关于它的计算,可以用下面的公式来计算:

如果对所有的 i=1,2,…m,有 Di-1,i=e-rΔt,则:

这里的E(e-rΔtVi(Si)|Si-1=s)代表一条件数学期望。
为了便于(4)的计算,我们引入新的变量:

通过计算,(4)可变化为:
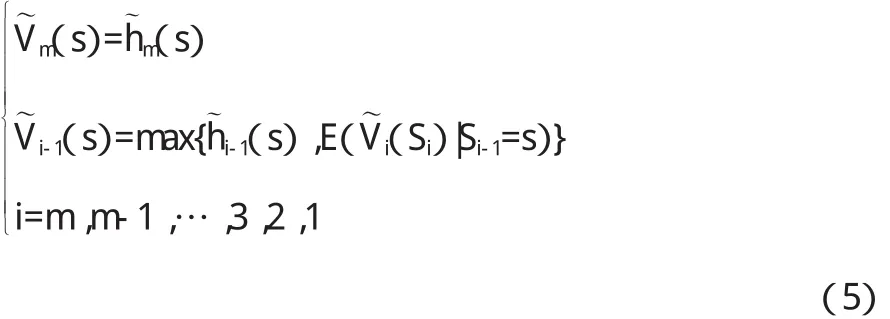
为了顺利进行下一步的计算,首先要求出(5)中的条件期望E(i(Si)|Si-1=s)。为此,我们假定:

这里,φ1(s),φ2(s),…,φM(s)是一些形式已知的基函数。在后面的计算之中,本文选取以下基函数:φr(s)=sr,r=0,1,2,…,M。由(6)可得:




蒙特卡洛方法主要利用(5)式计算V0(s),该方法通过以下步骤分步进行:
1.给定 S(0)=s的值。
2.根据式(1),先模拟 n条标的资产价格 S(t)变化的曲线,每条曲线上都有m个值,也即t1,t2,…,tm时刻的值为{S1j,S2j,…,Smj},j=1,2,…,n。
4.对于 i=m-1,…3,2,1,0按照下列步骤进行循环计算:
三、计算结果
我们假定用有限差分法计算出来的结果为“准确解”(该方法详细内容见[13]之中的介绍),然后将其与蒙特卡洛方法得出的结果进行比较分析。
在具体的计算过程中,本文设标的资产的平均收益率r=0.1,标的资产波动率σ=0.4,到期日T=1(年),合约执行价格K=10。
关于美式看跌期权,t=0时的价格V0(s)对不同的s计算结果(见下页表1)。
关于美式看涨期权,t=0时的价格V0(s)对不同的s计算结果(见下页表2)。
从表2中不难看出,模拟次数越多时,得到的数值解越接近“准确解”。
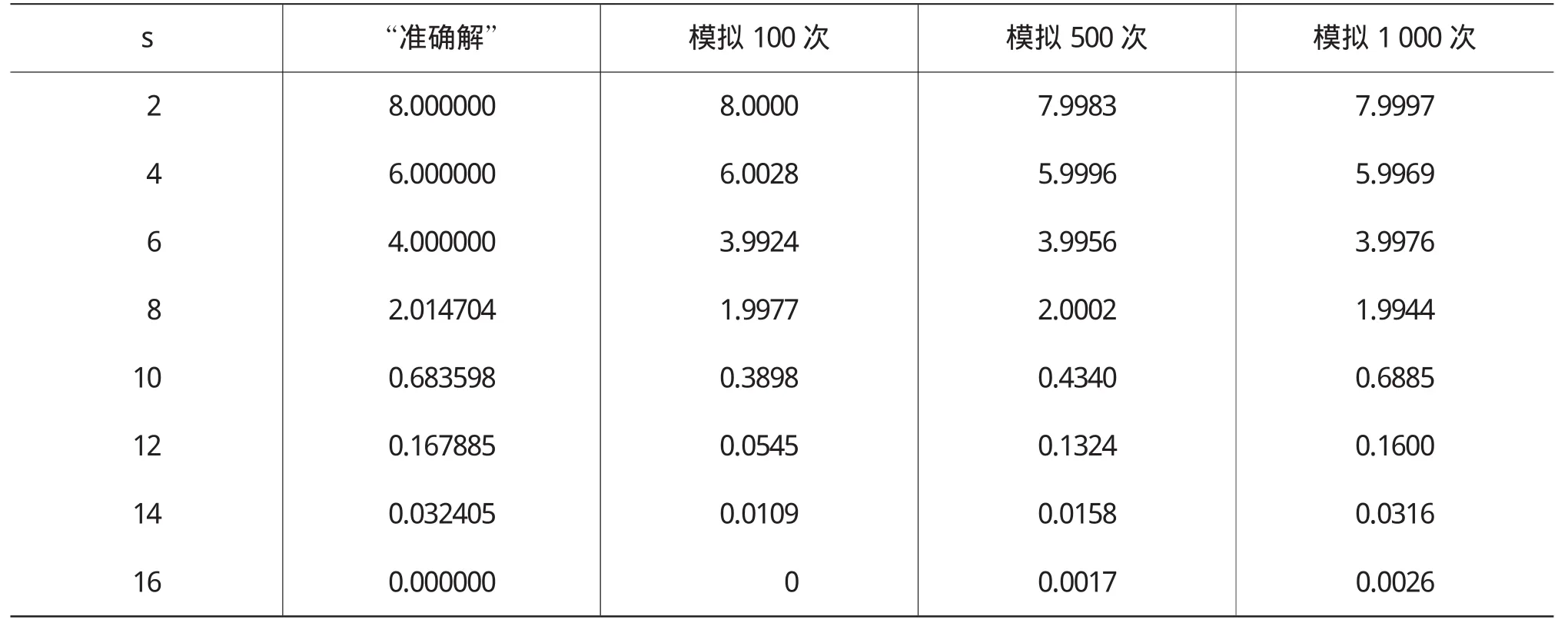
表1

表2
结论
本文讨论了美式期权定价的蒙特卡洛方法,我们根据美式期权的特点详细地制定了相应的数学模型和Matlab程序。本文比较了蒙特卡洛方法与有限差分法得到的数值结果,发现它们非常接近。相对于传统二项式、有限差分(隐式和显式)等方法,蒙特卡洛方法具备了更好的普适性,可推广用于各式期权价格的计算中,在实际应用中也就更能大显身手。但蒙特卡洛方法也有自己的缺点,那就是仿真结果不太精确,具有较大波动性,尤其是在在模拟次数较小的时候。为了提高精度,我们可以增加模拟次数。但是,蒙特卡洛方法具有一般性,相信本文的研究方法可以较好地解决其他各式期权价格的计算问题,同时,也可以将之推广应用于其他类型的金融衍生品的定价问题中。
[1]姜礼尚.期权定价的数学模型和方法[M].北京:高等教育出版社,2003.
[2]林群.微分方程数值解法基础教程:第2版[M].北京:科学出版社,2003.
[3]Robert.Tompkins.解读期权:第2版[M].陈宋生,崔宏,刘锋,译.北京:经济管理出版社,2004.
[4]Longstaff,Schwartz ES.Valuing American optionsby simulationasimpleleast squaresapproach[J].Reviewof Financial Studies,2001,(1):113-148.
[5]F.Black,M.Scholes,The pricing of options and corporate liabilities,J.Polit.Econ,1973,(3):637-654.
[6]张铁.美式期权定价问题的数值方法[J].应用数学学报,2002,(1).
[7]约翰·赫尔.期权、期货与衍生证券[M].北京:华夏出版社,1997.
[8]罗开位,候振挺,李致中.期权定价理论的产生和发展[J].系统工程,2000,(18).
[9]梁义娟,徐承龙.美式期权定价的数值方法[J].应用数学与计算数学学报,2013,(1).
[10]曹小龙,胡云姣.美式期权定价的拟蒙特卡罗模拟及其方差减小技术[J].北京化工大学学报:自然科学版,2014,(3).
[11]古丽丽,金朝嵩.美式看跌期权定价的控制变量法及其估值效率研究[J].经济数学,2007,(4).
[12]马俊海,刘凤琴,张义珍.关于美式衍生证券定价的数值分析方法的分析与评述[J].管理工程学报,2000,(4).
[13]P.Wilmott,J.Dewynneand J.Howison.Option Pricing:Mathematical Modelsand Computation[M].Oxford Financial Press,Oxford,1993.
