纺纱过程质量波动预测新方法

邵景峰，贺兴时，王进富，白晓波，雷 霞，刘聪颖

(1.长安大学信息工程学院，陕西西安 710064;2.西安工程大学管理学院，陕西西安 710048)

纺纱质量波动问题是纺织理论界长期探讨但又未能很好解决的一大难题［1-3］。在国外，如Selvanayaki等［4］将支持向量机方法应用于纱线强力的预测，Fattahi等［5］将模糊最小二乘回归方法应用于棉纱生产过程的控制，以及Mokhtar等［6］研究了织造过程质量与不确定因素之间的非线性关系，并由此提出了这种关系的检验方法等。随着理论的发展和研究的深入，涉及的变量和需要检验的关系越来越多［7］。如 Mohamed等［8］利用回归模型对棉纤维混合属性进行了预测，Mwasiagi等［9］利用混合算法(Hybrid Algorithms)构建了一种改善纱线参数性能的预测模型，以及Mardani等［10］利用有限元和多变量对影响纺纱张力的不确定性因素进行了分析。我国纺织学者从不同角度研究了纺纱质量波动问题［11］，提出了一些质量预测理论与方法，如杨建国等［12］借助统计学理论而提出的基于支持向量机的纱线质量预测模型，吕志军等［13-14］利用遗传算法的搜索寻优技术，对支持向量机的纱线质量预测模型的参数进行了优化，以及李蓓智等［15］针对支持向量机(SVM)在参数选择方面的费时问题，充分利用遗传算法的全局搜索能力，提出了一种基于遗传算法的SVM参数选取方法等。文献［16-17］从理论上分析了纺纱质量波动的关键因素，探讨了相关的预测方法与技术，如赵博等［18］通过神经网络与回归分析法来预测纱线质量。

综上所述，国内外学术界的主要注意力集中在纺纱质量预测模型与方法的构建上［19-21］，但对纺纱过程质量预测的另一面，即波动机制及规律性，以及各类不确定因素对纺纱质量成长过程的影响问题还少有研究。为此，利用纺纱过程产生的海量数据，以品种为关键词，从中探索纺纱质量特征值波动的规律性以及影响因素的产生机制，以及二者之间的相关关系，由此设计纺纱过程质量波动预测四步法，为纺纱质量实时在线检测提供新方法。

1 预测方法设计与建模

依据纺织设备传感器所采集、存储的海量数据，借助数据统计与分析方法，构建纺纱过程质量波动预测四步法，实现质量特征值波动过程的可视化，具体包括4个步骤:1)理论分析纺纱质量特征值波动的机制;2)在此基础上，对纺纱质量特征值波动的规律进行界定及表示;3)理论研究质量特征值与不确定因素之间的相互作用机制;4)在实时数据环境下，辨识影响因素的异常行为。

1.1 纺纱质量特征值波动机制分析

纺纱过程是一个多因素(如温度、湿度、原料、人、设备和环境等)、多工序相互作用的过程，易受到外部因素以及设备零部件的磨损、老化、锈蚀等内部因素的影响，使得纺纱质量形成过程中特征值总是存在着不能完全消除的波动。在理论上，通常将这种波动按大小和方向不同分为正常波动(即偶然误差)和异常波动(即系统误差)2种。

回顾文献［12-14］，纺纱质量特征值的波动与原料属性变量之间存在着非线性关系，更重要的是与工艺参数之间存在着非线性的函数关系，而且这种关系更难以用数学关系式进行表达。为深入分析引起纺纱质量特征值波动的原因，需进一步探究这种非线性关系，以及关系之间隐含的引起系统误差的根本原因。为此，从纺纱质量的输出特征值，以及工艺参数组合方式入手，构建如图1所示的函数关系。

图1 工艺参数与质量输出特征值之间关系图Fig.1 Relationship graph of technology parameters and characteristic value of quality output.(a)Fluctuation function for spinning quality characteristic value;(b)Corrected function k

以x表示工艺参数的不同组合，y表示纺纱质量的某种输出特性，则x与y的函数关系如图1(a)所示。可见，当x=x1时，其对应的质量输出特征值为y1，表示当x=x1时，x的波动误差为△x1，则相应地输出特征值的波动误差为△y1。当工艺参数的组合为x=x2时，x的波动误差为△x2，质量输出特征值为y2，输出特征值的波动误差为△y2。那么当△x1=△x2时，由图1(a)可见，△y1＞△y2，二者间并非呈线性关系。说明虽然工艺参数组合在x=x2点上很大程度上降低了质量输出特征值的波动，在一定程度上有效防止了纺纱质量的波动，但从图1(a)还可见，引发了一个新问题，即质量输出特征值的标准值M也增加了。

为此，通过纺纱工艺参数的组合方式，从中获取一个元素k，使元素k与质量输出特征值y之间呈线性关系。其中，元素k与质量输出特征值的线性关系如图1(b)所示，具体的线性关系表示为:

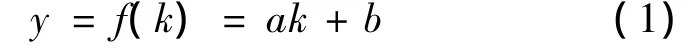
1.2 纺纱质量特征值波动规律表达

根据工艺参数组合方式与纺纱质量输出特征值之间的函数关系y=f(k)，质量输出特征值的波动误差△y可用输出特征值y与目标值y0之差来表示，即△y=y-y0。由于y0是一定值，y为一个可变值，则根据△y与y0之间的线性关系可知，△y为随机变量，并且与y0呈正相关关系。

由概率论统计理论可知，随机变量△y也应遵循一定的概率分布，而且这种概率分布在不同性质的不确定影响因素作用下，其分布不完全相同。就整个纺纱质量形成过程而言，多个相互独立的不确定因素在对质量特征值产生影响时，其分布可近似服从正态分布［22］，因此，对于确定的概率分布又可通过衡量数值集中和分散程度的数值特征(如μ和δ)来描述，而μ和δ的大小可由纺纱过程中的状态来决定，即波动误差△y遵循△y～N(μ，δ2)。

1.3 作用机制研究

根据人机系统工程学理论，从人、设备、材料、方法、测量和环境因素入手，将各类不确定因素划分为6 大因素集合，并记为 U1、U2、U3、U4、U5、U6，将其构成一个不确定因素集 U={U1，U2，U3，U4，U5，U6}。当然，集合U可根据因果分析图法并对其进行多次划分，使其形成多个子层。这样，通过各因素间的相关关系，可构建如图2所示的面向纺纱过程的人-机-环境脆性模型。

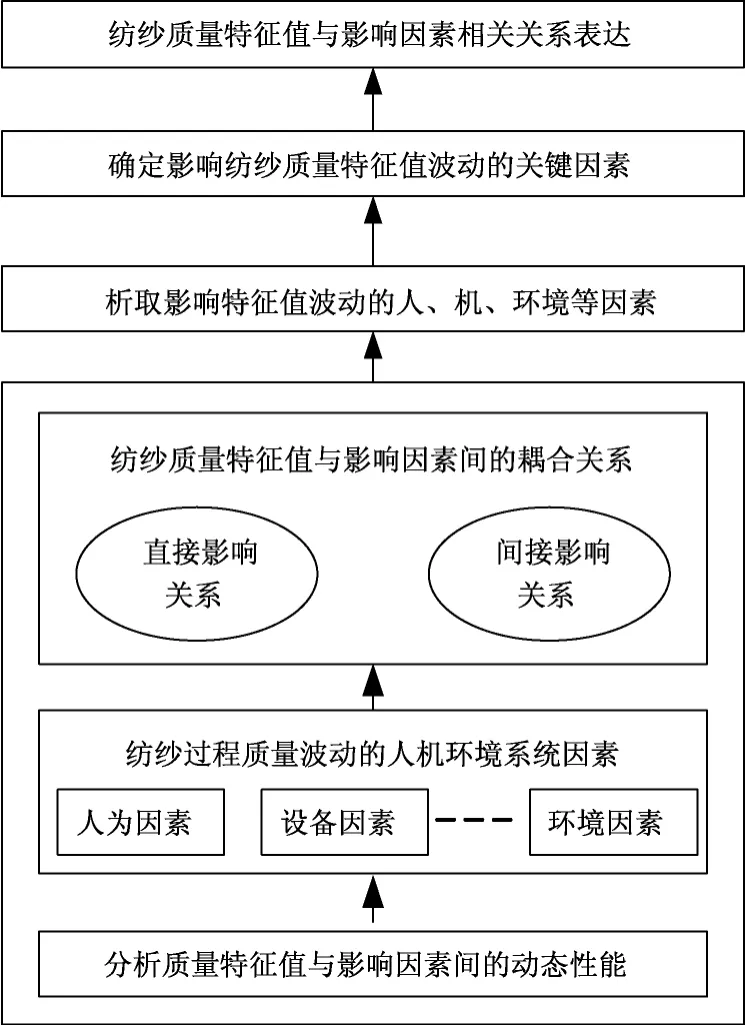
图2 人-机-环境脆性模型Fig.2 Man-machine-environment brittle model

依托人机环境系统工程学理论，令si表示加工过程中产生的异常事件，xi表示不确定因素，且i=1，2，…，n，则纺纱质量的形成过程 Qp表示为:

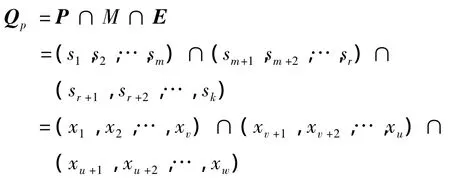
其中:P为人为影响因素集合，表示存在m个与人为因素相关的异常事件，例如挡车工、维修工等;M为设备因素集合，表示存在r-m+1个与设备相关的影响因素，如机台转速、电动机功率等;E为环境因素集合，表示存在k-r+1个与环境相关的影响因素，如温度、湿度、强电干扰等，k为影响质量波动的不确定性因素总数，且存在1≤m＜k，1≤r＜k。

若以X表示影响纺纱过程质量波动的人-机-环境因素，则 E=(x1，x2，…，xk)，相应地(x1，x2，…，xs)表示人为因素，(xs+1，xs+2，…，xu)表示设备因素，(xu+1，xu+2，…，xk)表示环境因素，且1≤s＜ k 1≤u＜k。现通过纺纱质量形成过程的表达式Qp，可将影响纺纱质量波动的各类不确定因素间的相互作用过程表示为:Qp=(K，O，R)，其中:K表示影响质量波动的不确定因素总数;O表示不确定因素间的交互集合;R表示质量波动与不确定因素之间的关系集合，并且R可表示为R=(K∪O)，则Qp将构成一个无向图，其中点集由K∪O组成，而边集由关系R组成。这样，在纺纱过程中，根据质量输出特征值y=(y1，y2，y3，…，ym)，影响因素 x=(x1，x2，x3，…，xn)，以及不确定因素隶属函数的向量U(x)，构建不确定因素间的关系图Q=K∪(K∪O)，则细化后不确定性因素可表示为 x11，x12，x13，…，x1n;x21，x22，x23，…，x2n;x31，x32，x33，…，x3n;…;xn1，xn2，xn3，…，xnn。因此，整个纺纱质量与不确定因素间的相互作用过程可表示为:Qp⇒R(((x11→x12→x13)→x1)∪((x21∪x22∪x23)→x2)∪((x31→x32→x33)→x3)，…，→xn)。

1.4 影响因素行为特征辨识

当整个纺纱质量形成过程处于稳态时，通过纺纱质量形成过程关系式Qp⇒P∩M∩E可知，P、M、E对应的不确定因素对纺纱质量特征值的影响遵循一定的分布规律。故在实时纺纱过程中，若自相关过程满足平稳序列的条件，则可认为影响纺纱质量波动的不确定因素的行为具备了稳态的统计性质，可分析引起纺纱质量波动的因素之间，以及同品种不同数据之间的数据依赖关系。而时间序列模型TARCH(p，q)为不确定因素的行为特征辨识提供了基本方法，具体过程如下。

在自回归条件异方差模型 (ARCH)［23］的基础上，将其进行变换形成TARCH(p，q)模型，即:

式中:αi表示质量特征值波动前期关键因素对本次波动的影响程度;βj表示特征值波动前期次要因素对本次波动的影响程度;p、q分别表示TARCH项的滞后阶数。

式(2)表明:在自相关稳态下，由不确定因素的异常行为引起的纺纱质量波动，明显大于数据采集值在独立情况下的质量波动，而这些波动造成的质量损失是由纺纱过程自相关所造成的。为合理界定不确定因素的行为特征，当纺纱过程质量特征值的均值不发生变化时，将p、q值置为1，利用如式(3)、(4)所示的TARCH(1，1)模型对应的均值与条件方差进行控制变量的输入，对自相关平稳过程进行调整。

上式中，如果 εt－1≥ 0 且 dt－1=0，或者 εt－1＜ 0 且dt－1=1，则 εt－1≥ 0 对产生的影响为 α，而当εt－1＜ 0 则对所产生的影响为α+γ。故在γ≠0的前提下，纺纱质量特征值的波动过程呈现不对称性。而对TARCH(1，1)模型而言，εt－1与 dt－1的取值对所产生的影响也存在不对称性。

2 实验验证

实验方案:在相同条件下，测试系统、人、设备、环境等不确定因素对纺纱质量的影响程度。设定室温为20℃，相对湿度为65%。

方案一:从设备传感器直接测试数据(简称“测试数据”)。用Uster Tester III测试纱线的线密度和变异系数(CV值)，用Sirolan-tensor测试纤维束强力，用Tensorapid测试纱线强度和伸长。

方案二:从监控系统中统计纺纱数据(简称“监测数据”)。主要通过VS2008+SQL Server2005开发纺织过程集成监控系统，该系统可对各纺纱子系统的实时数据进行集成。

在相同班次、设备、机型条件下，2个实验方案同时进行。根据纺纱机工艺计算公式［24］，当罗拉直径为25 mm时，其前罗拉转速通常为240 r/min，则时间间隔△t=4 s，即产生2个脉冲周期。对方案一的每个测试结果重复5次，将数据结果按照成纱品种分类并手工输入纺织过程监控系统的一张临时数据表(TestData)。在相同的实验条件下同时进行，数据采集结果同样以成纱品种为主键在自动存入系统数据库历史数据表(HistoryData)的同时在终端界面实时显示。

按照成纱品种类别，取时间间隔△t=4 s，并从2个数据表(TestData与HistoryData)中统计出纺纱质量的主要特征值(细度不匀，%;细节，个/km;粗节，个/km;强度，cN/tex;断裂伸长，%)，对比分析相应的质量特征值，并计算出二者的误差，结果如表1所示。

由表1可见，在时间间隔△t=4 s内，相同工艺、相同规格的纱线质量特征值的误差不同，而且误差间的变化趋势并不遵循一定的规律(如正态分布)，误差数据与质量输出特征值之间很难建立一种线性关系，具体过程如下。

1)在时间间隔△t=4 s内，在每个数据采集点上，通过△x与△y之间的数值关系，对2种数据采集方式所形成的质量误差进行仿真，其结果如图3所示。可见，通过设备传感器直接测试和监控系统统计得到的质量特征值之间存在误差，而且误差主要分布在理论平衡点之下(＜5%)，这充分说明由现场监控系统采集、处理、统计、分析出的纺纱质量特征值波动较大。为此，在时间间隔内，等间距增加数据采样点，使采样时间间隔△t=0.25 s，通过求导计算得到a=0.8140，b=2.0351，构成如图4(a)所示的线性关系图，从中获取最优k值，以修正y，最终形成如图4(b)所示的工艺参数组合与质量输出特征值。

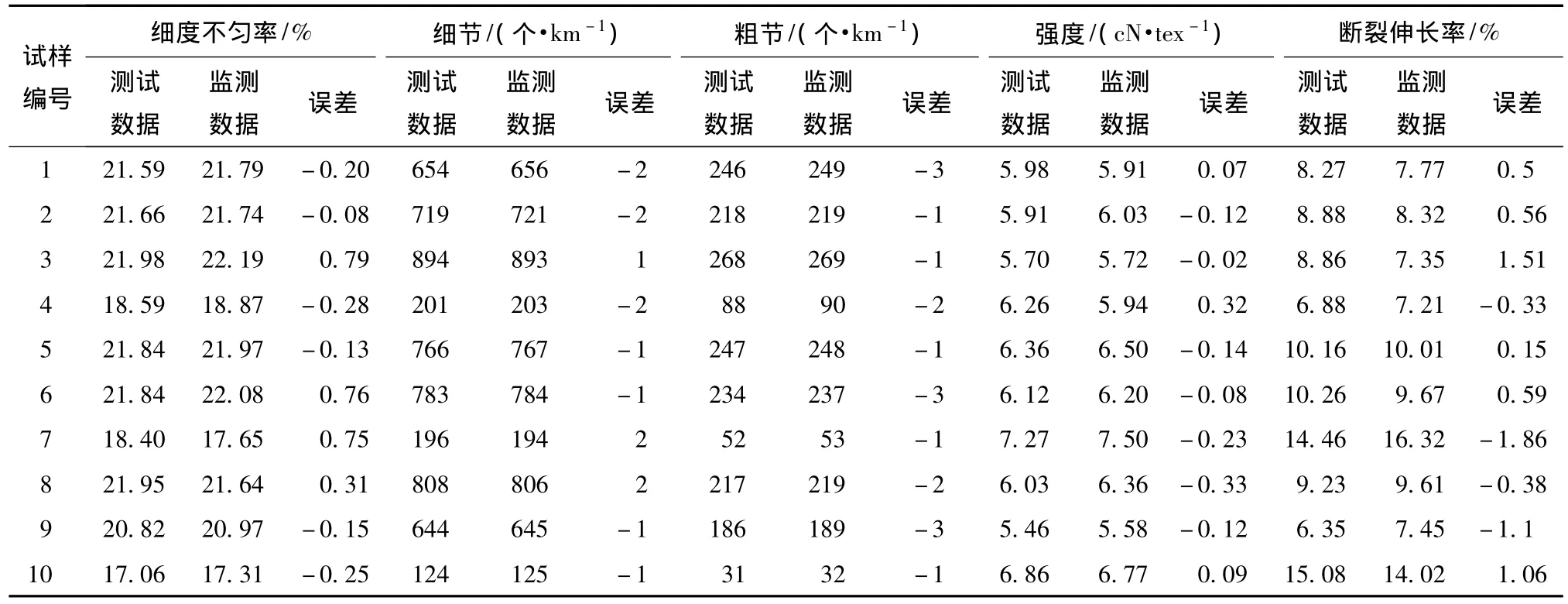
表1 测试与监测数据误差对照表Tab.1 Error comparison table between testing and monitoring data

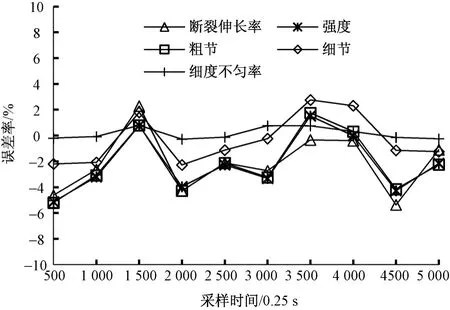
图3 数据误差仿真结果Fig.3 Simulation results of data errors

从图4可见，经函数y=0.814 0k+2.id=i对质量输出特征值y进行修正后，其△y随着斜率减小而降低，相应地M值也减小，从设备传感器直接获取质量数据，其数据计算结果精度明显高于上位机监测器所采集的数据，并且函数y=f(x)的斜率降低，对应的函数曲线趋于直线。

2)在1)的基础上，为进一步探索影响Qp形成过程中纺纱质量特征值波动的规律性，结合表1的波动误差，形成如图5所示的误差源判别图，从2个实验方案中判断纺纱质量特征值波动特征的异同，并从中界定影响Qp形成过程的主要根源。

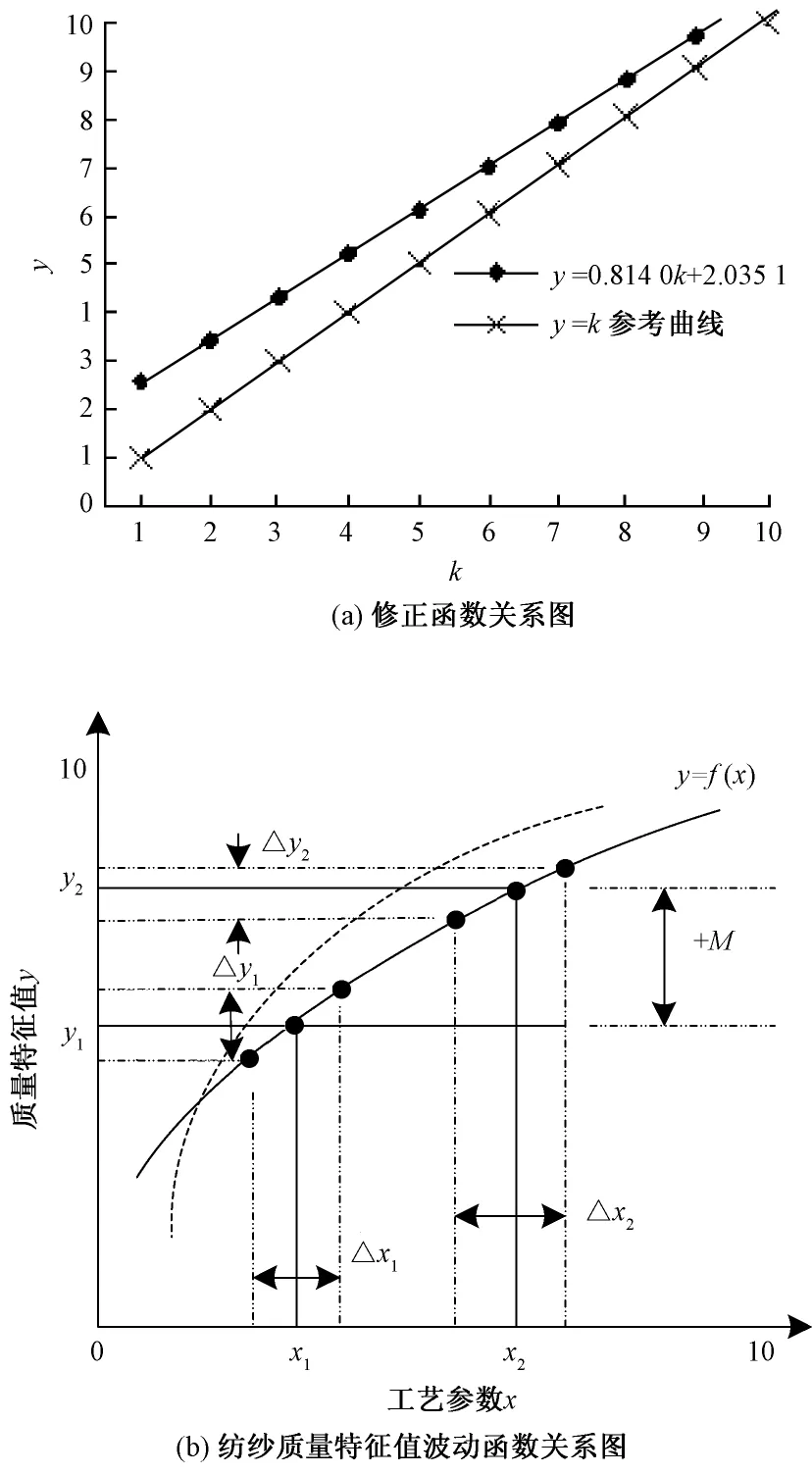
图4 改进的工艺参数与质量输出特征值关系图Fig.4 Improved relationship graph of technology parameters and characteristic value of the quality output.(a)Relationship of the corrected function k;(b)Fluctuation function relationship for spinning quality characteristic value

图5 质量数据误差源判别图Fig.5 Error source discrimination diagram of quality data

从图5可见，由监测系统采集处理的监测数据误差曲线基本位于测试数据误差曲线之上，说明监测系统采集的纺纱质量数据产生的数据误差相对较大，故引起纺纱质量特征值波动的主要源泉在于监测系统，但是，这种数据误差的变化趋势将随着纺纱过程的不断推进，曲线趋于平稳下降趋势，且总体小于3%，能满足纺织企业既定误差(＜5%)要求。

3)在确定了质量数据误差源后，结合表1中的数据，构建如图6所示的不确定因素间的关系图Q=K∪(K∪O)，并令原料、人、方法、设备、测量和环境因素分别对应的元素为 x1、x2、x3、x4、x5、x6，这样因素集K的样本数为6，O为因素交集，故图中横坐标表示因素交集数，纵坐标表示因素关系边集R=(K∪O)，且 R∈［0，1］，由此从中探究影响质量波动的关键因素。

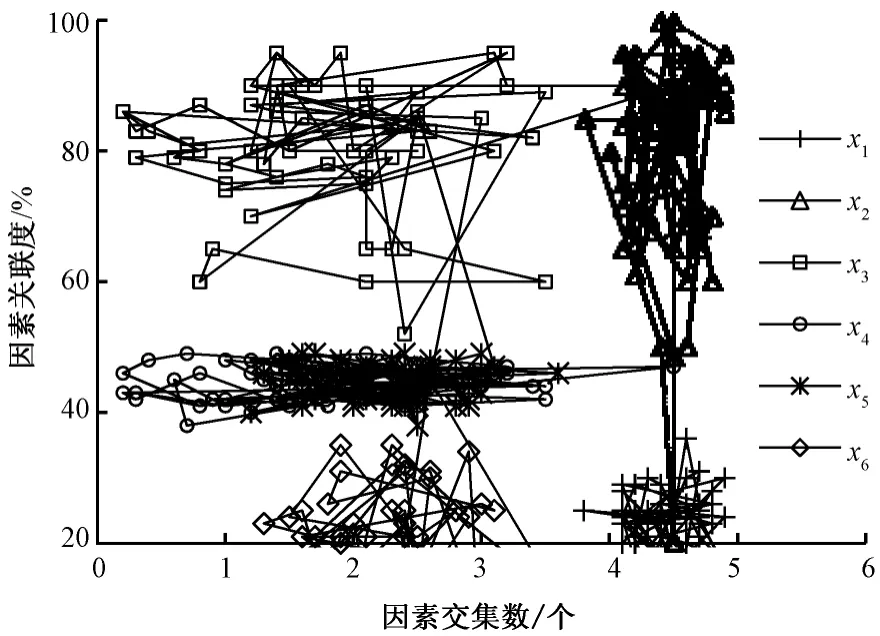
图6 不确定因素间关系图Fig.6 Relationship for uncertain factors

由图6可见，在这个已给定的多因素影响集中，因素集 x1∩x2≠φ，x3∩x4∩x6≠φ，且具有高相关度，而因素集 x2∩x3∩x4∩x5∩x6≠φ，但具有低相关度。而且因素集x1∩(x2∪x3∪x4∪x5∪x6)=φ，相互间相关度为零。但是，x1表现出的直接影响关系可直接影响纺纱质量，而 x2、x3、x4、x5、x6因素表现出的间接影响关系除对纺纱质量形成过程产生影响外，各因素之间也相互影响，其中因素集x3、x4、x5、x6之间具有高相关度，而其与x2具有低相关度。

4)在时间间隔△t=0.25 s，计算出纺纱质量波动率的基本统计特征值，即:质量波动率均值为-1.008、标准差为3.2152，说明当△t=0.25 s时，纺纱质量波动率呈下降趋势。偏度值为-0.0254，体现出纺纱质量特征值的波动具有左倾斜性，并且峰度值达到7.1692(＞3)，雅克贝拉检验值为835.42，结果表明纺纱质量特征值的波动过程并不服从正态分布。同时，有显著性差异P＜0.05，说明整个纺纱质量特征值波动过程具有自相关性。

为进一步辨识在自相关稳态下不确定因素的影响行为，通过分析同品种不同数据之间的数据依赖关系，采用低阶且变量参数较少的TARCH(1，1)模型进行估计质量特征值波动过程的自相关性，形成的TARCH(1，1)估计的拟合结果中，赤池信息量准则(AIC)为 -6.423，Q统计量为0.546，结果表明TARCH(1，1)模型对纺纱质量特征值波动过程的自相关性具有良好的估计，并且AIC值越小则估计结果越好。而且，拉格朗日乘数检验统计量为0.755，说明TARCH(1，1)模型在自相关稳态下对不确定因素异常行为的辨识和对纺纱质量损失的补偿具有较好的有效性。由此，形成TARCH(1，1)模型的估计结果如下。

均值方程为:

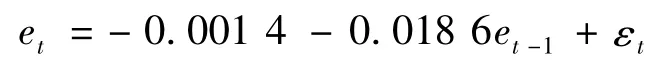
条件方差为:

综上所述，结合图6和TARCH(1，1)模型，当时间间隔△t=0.25 s时，纺纱质量形成过程中各影响因素实时在线爆发时的概率分布图如图7所示。

可见，在同一时间间隔△t=0.25 s内，随着纺纱过程纺纱质量的不断成长，x3(方法)、x1(原料)、x4(设备)三因素的爆发概率较大，概率均值依次接近46%、29%、13%，可视为影响纺纱质量波动的关键因素，而且x3(方法)的脆性最易爆发且概率最高，视为引起纺纱质量波动的最关键因素。

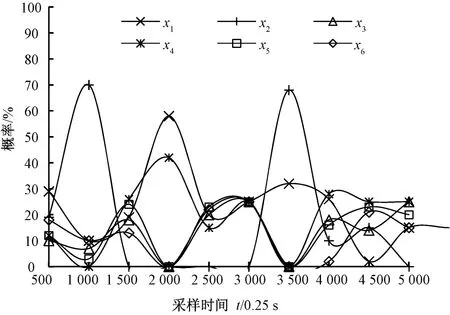
图7 不确定因素异常概率Fig.7 Probability distribution diagram for uncertainty factor

3 结论

从纺纱质量特征值波动问题角度出发，依托人机环境系统工程学理论，从4个方面探索了纺纱质量特征值波动的内在机制，构建了纺纱质量特征值波动预测四步法。并且结合现场的实时在线数据，通过2种实验方案的仿真和对比，实现了纺纱过程中从质量特征值的波动成因、规律到影响因素的产生机制及与纺纱质量特征值之间相关关系表达，再到影响因素异常行为辨识的全方位分析。对纺纱过程质量特征值波动内在机制的研究，不但有利于整个纺纱质量的事前预测和可视化管理，而且有利于实现基于实时数据的纺纱质量在线检测，从而保证企业、乃至车间整个制造过程的连续性，并为纺织企业解决制造过程的异常事件而提供理论依据。

［1］ FATTAHI S R，SEYED A H，TAHERI S M.Two-way prediction of cotton yarn properties and fiber properties using multivariate multiple regression［J］.Journal of the Textile Institute，2011，102(10):849-856.

［2］ MALIK S A，TANWARI A，SYED U，et al.Blended yarn analysis:part I-influence of blend ratio and break drafton mass variation， hairiness， and physical properties of 15 tex PES/CO blended ring-spun yarn［J］.Journal of Natural Fibers，2012，9(3):197-206.

［3］ MATTESA， PUSCH T， CHERIFC.Numerical simulation of yarn tensile force for dynamic yarn supply systems of textile machines［J］.Journal of the Textile Institute，2012，103(1):70-79.

［4］ SELVANAYAKI M，VIJAVA M S，JAMUNA K S，et al.An interactive tool for yarn strength prediction using support vector regression［C］//Proceedings of the 2nd International Conference on Machine Learning and Computing(ICMLC 2010)，2010:335-339.

［5］ FATTAHI S，TAHERI S M，RAVANDI H.Cotton yarn engineering via fuzzy least squares regression［J］.Fibers and Polymers，2012，13(3):390-396.

［6］ MOKHTAR S，BEN A S，SAKLI F.Optimization of textile parameters of plain woven vascular prostheses［J］.Journal of the Textile Institute，2010，101(12):1095-1105.

［7］ FALLAHPOUR A R，MOGHASSEM A R.Spinning preparation parameters selection for rotor spun knitted fabric using VIKOR method of multicriteria decisionmaking［J］.Journal of the Textile Institute，2013，104(1):7-17.

［8］ MOHAMED N，SAMAR A E.Prediction of some cotton fiber blends properties using regression models［J］.Alexandria Engineering Journal，2008，47(2):147-153.

［9］ MWASIAGI J I，HUANG X B，WANG X H.The use of hybrid algorithms to improve the performance of yarn parameters prediction models［J］.Fibers and Polymers，2012，13(9):1201-1208.

［10］ MARDANI M N，SAFAR J M，AGHDAM M M.Finiteelement and multivariate analyses of tension distribution and spinning parameter effects on a ring-spinning balloon［J］. Journal of Mechanical Engineering Science，2010，224(2):253-258.

［11］ 邵景峰，王进富，马晓红，等.一种影响织造过程的不确定性预测理论模型［J］.纺织器材，2012，39(6):57-62.SHAO Jingfeng，WANG Jinfu，MA Xiaohong，et al.A theoretical model of the uncertainty for casting on weaving process［J］.Textile Accessories，2012，39(6):57-62.

［12］ YANG J G，LV Z J，LI B Z.Quality prediction in complex industrial process with support vector machine and genetic algorithm optimization:a case study［J］.Applied Mechanics and Materials，2012，232:603-608.

［13］ 吕志军，杨建国，项前.基于遗传算法参数优化的纱线质量预测技术［J］.东华大学学报:自然科学版，2012，38(5):519-523.LÜ Zhijun，YANG Jianguo，XIANG Qian.GA based parameters optimization on prediction method of yarn quality［J］.Journal of Donghua University:Natural Science Edition，2012，38(5):519-523.

［14］ LÜ Z J，XIANG Q，YANG J G.A novel data mining method on quality control within spinning process［J］.Applied Mechanics and Materials，2012，224:87-92.

［15］ 李蓓智，李利强，杨建国，等.基于GA-SVM 的质量预测系统设计和实现［J］.计算机工程，2011，37(1):167-169.LI Beizhi，LI Liqiang，YANG Jianguo，et al.Design and implementation of quality prediction system based on GA-SVM［J］.Computer Engineering，2011，37(1):167-169.

［16］ PEI Z G，CHEN G，LIU C，et al.Experimental study on the fiber motion in the nozzle of vortex spinning via high-speed photography［J］.Journal of Natural Fibers，2012，9(2):117-135.

［17］ LÜ J，CAO C H.Prediction of yarn quality based on differential evolutionary BP neural network［C］//Proceedings of the 4th International Conference on Computational and Information Sciences(ICCIS 2012)，2012:1232-1235.

［18］ ZHAO B.Prediction of thin place of polyester/cotton ring yarn properties from process parameters by using neural network and regression analysis［C］//Proceedings of the 7th International Conference on System of Systems Engineering(SoSE 2012)，2012:18-20.

［19］ LIU H，ZHANG Y，CHEN L，et al.Development and characterization of flexible heating fabric based on conductive filaments［J］.Journal of the International Measurement Confederation，2012，45(7):1855-1865.

［20］ KELLY C M，HEQUET E F，DEVERA J K.Breeding for improved yarn quality:modifying fiberlength distribution［J］.Industrial Crops and Products，2013，42(1):386-396.

［21］ FAROOQ A，CHERIF C.Development of prediction system using artificial neural networks for the optimization ofspinning process［J］.Fibers and Polymers，2012，13(2):253-257.

［22］ NURWAHA D，HAN W L，WANG X H.Effects of processing parameters on electrospun fiber morphology［J］.Journal of the Textile Institute，2013，104(4):419-425.

［23］ MOHAMMADI T，TAGHAVI M，BANDIDARIAN A.The effect of exchange rate uncertainty on import:TARCH approach ［J］.International Journal of Management Business Research，2011，1(4):211-220.

［24］ SALVINJIA P，PETRULISA D.Influence of twisting on linen fancy yarn structure［J］.Journal of Natural Fibers，2014，11(1):74-86.