平板焊接接头裂纹扩展中残余应力重分布的数值模拟

李良碧，张沛心，周 宏

（江苏科技大学 船舶与海洋工程学院，江苏 镇江212003）

0 前言

焊接过程中，金属受高温融化产生了塑性变形，在冷却时会产生较大的残余应力。残余应力与外载荷共同作用，可能会危害焊接结构的安全性。此外，焊接接头的焊缝附近是焊接结构的疲劳热点部位，较易产生疲劳裂纹。有裂纹的结构在承受交变载荷作用时，裂纹会发生扩展，从而导致焊接接头的疲劳断裂。焊接残余应力会影响结构的疲劳行为，残余应力场的存在会使焊接结构的疲劳裂纹扩展呈现出与非残余应力场中扩展特性不同的一面[1]。另外，在交变载荷作用下，疲劳裂纹尖端会产生塑性区，其焊接残余应力会不断地松弛和释放[2]。现有研究表明，基于焊接残余应力影响的结构疲劳强度的评估相当复杂，主要是由于焊接残余应力场在疲劳裂纹扩展过程中会发生重分布[3]。

目前，国内外已有相关学者对焊接残余应力与疲劳裂纹扩展之间的关系进行了一些预测。其中，Barsoum等人[4]利用Forman公式求得考虑残余应力影响的疲劳裂纹扩展速率，进而得到残余应力场对疲劳裂纹寿命的影响；杨化仁等人[5]采用切割应力释放法研究了残余应力对疲劳裂纹扩展的影响，并测得了残余应力随裂纹长度变化的规律；但此类研究往往采用繁琐的解析法或造价较高的实验法，且针对高强度钢平板焊接接头裂纹扩展中残余应力重分布的研究较少。因此，采用有限元模拟的方法，对高强度钢平板接头表面裂纹扩展中残余应力的重分布进行数值模拟研究。本研究对于更加合理地理解残余应力对裂纹结构疲劳强度的影响具有重要意义。

1 相关理论

1.1 焊接残余应力数值模拟相关理论

由于焊接过程是金属受热、融化、冷却等的一系列过程，随着高温热源的移动以及焊后的快速冷却，在焊缝及其附近不可避免地产生了复杂的残余应力场。本研究采用ANSYS的热分析模块来模拟厚板多层多道焊的焊接过程，主要分为温度场分析和残余应力场分析两个方面。

1.1.1 焊接温度场

分析焊接过程中的温度场变化是残余应力场分析的前提。随着热源的移动，整个焊件的温度随着时间和空间变化，对于焊接材料内部任意一点的瞬态温度 T（x，y，z，t）满足以下微分方程[6]

1.1.2 焊接应力应变场

（1）焊接应力应变场是一个复杂的非线性问题，在热弹塑性分析的基础上，做以下假定[7]。

a.材料的屈服满足Von Mises屈服准则；b.塑性区内的行为服从塑性流动准则和强化准则；c.弹性应变、塑性应变与温度应变是不可分的；d.与温度有关的力学性能、应力应变在微小的时间增量内线性变化。

（2）材料在塑性状态的应力应变关系为

式中 [D]为弹性或弹塑性矩阵；{C}为与温度有关的向量；{dσ}、{dε}和 dT 分别为单元的应力增量、应变增量和温度增量。

（3）平衡方程。

每次温度增加后，节点的位移增量{dδ}可由下列平衡方程求得

式中 [K]为集成总刚度矩阵；{dF}为总载荷向量。

（4）有限元求解过程。

热弹性有限元分析时，首先将结构划分成有限个单元，然后加上由温度场计算出的温度增量。每次温度场增量加载完毕后，由式（3）的方程得到节点的位移增量 {dδ}，由式（4）求得单元应变增量{dε}，最终由式（2）求得单元应力增量{dσ}。

式中 [B]为联系单元中应变与节点位移向量的矩阵。

1.2 疲劳裂纹扩展数值模拟相关理论

近年来，国内外诸多学者采用多种方法来预测疲劳裂纹扩展寿命。目前，在线弹性断裂力学范围内，应用最广泛的方法依然是1963年Pairs和Erdogan在试验基础上提出的疲劳裂纹扩展规律公式，即Pairs公式[8]

式中 a为裂纹尺寸；N为应力循环次数；da/dN为裂纹扩展速率；C和m为裂纹扩展性能参数，由试验确定；ΔK为应力强度因子幅度。

式中 Kmax、Kmin为裂纹处应力强度因子的最大值与最小值；f为结构几何与裂纹尺寸的函数；Δσ为裂纹处应力幅值。

可用迭代法计算出裂纹稳定扩展阶段的寿命

式中 a0初始裂纹尺寸；ac为裂纹尺寸。

2 完整平板对接接头初始残余应力的数值模拟

2.1 完整平板焊接接头模型

平板焊接接头采用Q345高强度钢制造，由两块250 mm×125 mm×38 mm的钢板对接焊接而成，其中焊缝尺寸为10 mm×250 mm×38 mm，其几何模型及尺寸如图1所示。坐标原点（0，0，0）设在焊接接头左下角，坐标系如图1所示，其中x轴垂直焊缝长度方向，y轴沿焊缝长度方向，z轴沿板厚方向。

根据文献[9]，由于平板焊接接头在焊趾处较易萌生裂纹，因此将初始裂纹设在焊趾处，为半椭圆形表面裂纹，裂纹中心点（即裂纹与焊接接头上表面相交形成的面的中心）的坐标为（135 mm，125 mm，38 mm），上表面如图1所示。

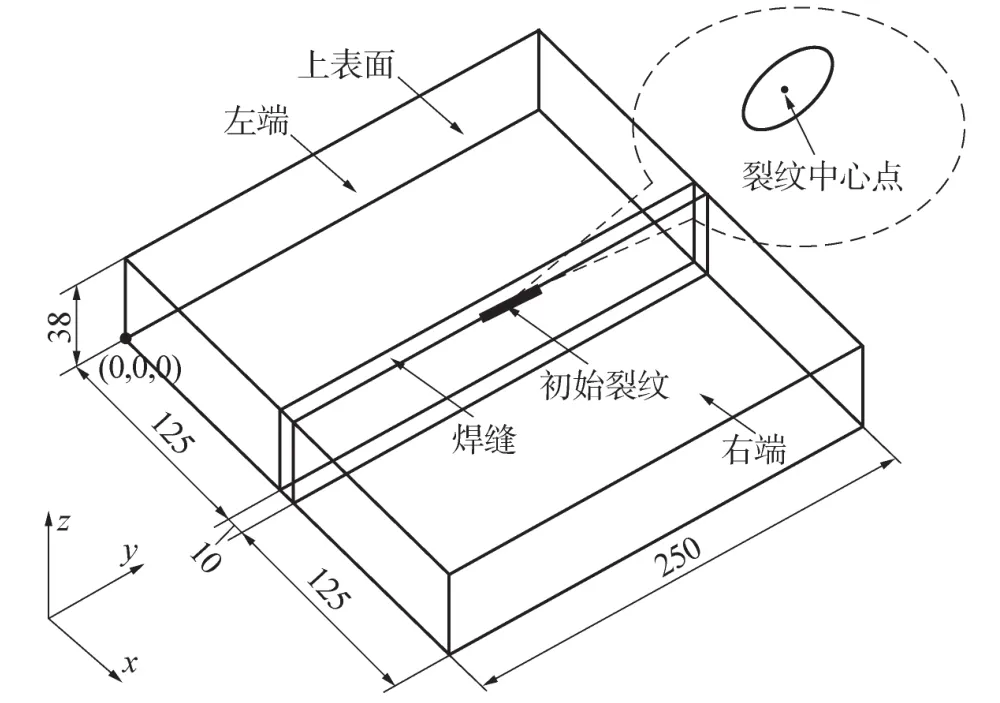
图1 几何模型及尺寸（单位：mm）

由于焊缝附近为研究的重点，因此在划分网格时，细分焊缝附近的单元。由于模型的对称性，在此仅列出图1中左侧钢板加焊缝的有限元模型，如图2所示。为方便表示残余应力在各路径下的变化曲线，将3条主要路径定义为：路径1与y轴平行，位于焊接接头上表面沿焊缝长度（裂纹长度）方向且通过裂纹中心点，d1表示路径1上某节点到裂纹中心点的距离；路径2与x轴平行，位于焊接接头上表面垂直焊缝长度方向且通过裂纹中心点，d2表示路径2上某节点到裂纹中心点的距离；路径3与z轴平行，并沿板厚（裂纹深度）方向且通过裂纹中心点，d3表示路径3上某节点到裂纹中心点的距离（见图 2）。

图2 路径的定义

表1 Q345钢的力学性能

图3 不同温度下的应力应变曲线

2.2 材料属性

Q345钢的屈服强度为345 MPa，极限强度为460 MPa。图3和表1分别给出了Q345钢在不同温度场下的材料性能和力学性能[10]。

2.3 完整结构初始焊接残余应力的数值模拟

采用ANSYS的热分析模块和生死单元技术模拟厚板多层多道焊的焊接过程，将焊缝沿板厚方向分为5层[13]。首先，计算焊接温度场，然后采用间接耦合法计算应力场。在计算应力场时，为防止模型发生刚体位移，对其四个角边刚性固定。由于x方向的残余应力为影响结构疲劳裂纹扩展的主要应力，在此仅研究x方向（见图1）的残余应力。

热应力分析结束后，待模型充分冷却，得到3条路径下x方向的初始焊接残余应力σxini的分布规律如图 4 所示（路径 1、2、3 以及 d1、d2、d3的定义如图 2所示）。

图4 不同路径的σxini

由图4可知，平板焊接接头在无裂纹时，在沿焊缝长度方向，σxini在焊缝长度中心附近拉应力较大（见图4a），最大值为86.56 MPa，在焊缝长度两端急剧减小并转变为压应力；在垂直焊缝方向（见图4b），σxini主要为焊接残余拉应力且呈双峰曲线分布，最大值出现在两个焊趾处，为168.47 MPa；在沿板厚方向（见图4c），在靠近上下表面的两层焊道残余拉应力最大，最大值为168.79 MPa，在板厚中心残余应力则较小。

3 产生初始裂纹后的残余应力变化

3.1 初始表面裂纹尺寸的选择

采用ZenCrack软件模拟初始表面裂纹。ZenCrack是ZenTech公司开发的3D高级裂纹扩展行为分析软件，可分析循环载荷作用下的3D疲劳裂纹扩展行为。

假定初始裂纹形状为半椭圆形，并根据文献[11]的结论，取初始裂纹长度2c0=3 mm，深度a0=1.14 mm，初始裂纹面及其附近网格如图5所示。

为方便表示裂纹附近的残余应力最大值出现位置，在初始裂纹面的几个特殊位置标记序号，其中①位于路径1上，表示裂纹前缘与平板表面相交的两个裂尖处；②位于路径3上，表示裂纹前缘深度最深的裂尖处；当裂纹发生扩展时，①的位置随裂纹的长度2c变化，②的位置随裂纹的深度a变化。

3.2 初始裂纹产生后的焊接残余应力重分布

设定好初始裂纹的各参数后，进行焊接接头初始裂纹产生后的残余应力重分布有限元分析，得到x方向的焊接残余应力σxinc的重分布规律，并与初始焊接残余应力σxini进行对比，如图6所示。

由图6可知，当焊接接头产生初始表面裂纹时，x方向的残余应力大小和分布规律均发生了变化。主要表现为：

a.在路径1（沿焊缝长度方向），σxinc转变为双峰曲线，两个拉应力峰值分别出现在两个裂尖①处（见图5a），为122.8 MPa，两个拉应力峰值的横坐标差值（Δd1）即为初始裂纹的长度c0。

图6 σxinc与σxini的对比

b.在路径3（沿板厚方向），残余拉应力最大值由下表面两层焊道的相交处转变到裂尖②处且最大值为137.8 MPa；其中，图6b曲线起点的横坐标d3等于初始裂纹的深度a0。

c.在路径2（垂直焊缝方向），σxinc主要为压应力，并由双峰曲线转变为单峰曲线，在裂纹附近压应力较大，而在远离裂纹处σxinc趋于0。为清晰地表示路径2下裂纹附近残余应力的变化规律，放大图6c中的部分曲线，如图6d所示，图中曲线断开的距离（Δd2）即为裂纹在路径2下的张开距离。

4 循环载荷作用下疲劳裂纹扩展中的残余应力重分布

4.1 疲劳载荷

由于I型裂纹是工程中最常见、最易于引起断裂破坏的裂纹[9]，为模拟其受力状态，在残余应力分析结束后，撤销其应力分析的边界条件，然后将焊接接头左端固定，右端施加沿x轴正向（见图1）、大小为15 kN的轴向拉伸载荷(此时焊缝附近的最大拉应力为310 MPa，约为0.9σs），载荷作用于右端面，为均布载荷。焊接残余应力与外载荷产生的工作应力相叠加，将作为控制疲劳裂纹扩展的应力。

4.2 疲劳裂纹扩展参数设置

裂纹扩展规律选择Paris公式[12]，其中材料常数 c=5.41936e-35，m=4.0247[7]；应力比 R=0.1；裂纹扩展的轮廓如图5b所示。

4.3 残余应力重分布的数值预报

图7为疲劳载荷循环分别为259次、661次和1 038次时裂纹附近x方向的应力分布云图。由图7可知，在裂纹扩展中，裂纹前缘拉应力较大，将促进裂纹的扩展。而裂纹前缘向模型表面拉应力逐渐减小，并转变成压应力。

循环载荷卸载后，得到裂纹扩展中的残余应力重分布规律，如图8所示。x方向的焊接残余拉应力最大值如表2所示（σxini为完整结构时的残余应力；σxinic为产生初始裂纹后的残余应力）。由于裂纹扩展后X方向的残余应力分布规律与σxinc的分布规律一致，仅应力水平有变化，故只列出了载荷循环259次、661次和1 038次时裂纹附近x方向的残余应力分布曲线（图8和表2中σ1、σ2、σ3分别表示载荷循环259次、661次和1 038次时x方向的残余应力）。为确保图像清晰，仅截取3条路径下，裂纹附近σx变化较大的范围内的曲线进行对比。

图7 裂纹附近的应力分布

图8 不同路径下的重分布结果

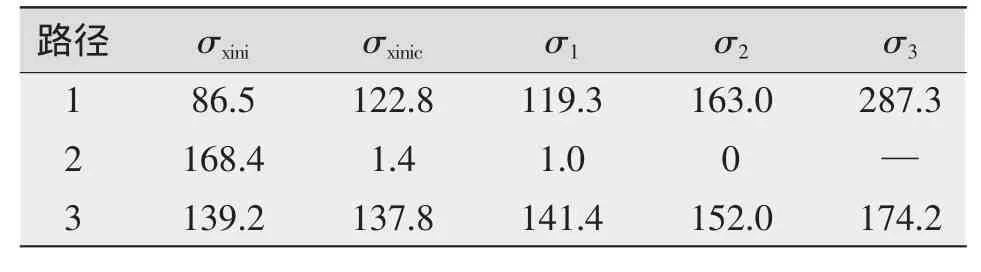
表2 拉应力最大值 /MPa

根据图8和表2可知，随着裂纹不断扩展：

a.在沿裂纹长度方向（路径1），残余拉应力最大值逐渐增加，且残余拉应力的两个峰值的横坐标（d1）的差值等于裂纹的长度2c。

b.在垂直裂纹长度方向（路径2），残余拉应力趋于0，在裂纹附近出现两个压应力峰值，且两个压应力的峰值横坐标（d2）的差值等于裂纹在路径2下的张开距离。

c.在沿裂纹深度方向（路径3），残余拉应力最大值逐渐增加，且残余拉应力最大值的横坐标（d3）等于裂纹深度a。

d.裂纹扩展时，平板焊接接头残余拉应力最大值位置与产生初始裂纹时相同，均出现在裂纹前缘的3个裂尖（即图5a的①②）处，并且在裂尖②处残余拉应力最大，残余拉应力促进了裂纹的扩展。

5 结论

（1）完整结构垂直焊缝长度方向（x方向）的初始焊接残余应力在焊缝附近较大，残余拉应力最大值出现在焊趾附近。

（2）当平板焊趾附近出现表面裂纹时，其垂直裂纹长度方向（x方向）的残余应力的分布规律和应力状态均会发生一定的变化。在裂尖处，即裂纹前缘与模型表面相交的两个端点以及裂纹前缘最深处的残余拉应力较大，并且裂纹前缘最深处的残余拉应力最大。

（3）随着裂纹的扩展，裂纹附近垂直焊缝长度方向的残余应力与产生初始裂纹时的分布规律一致，仅应力状态发生了变化。沿裂纹长度方向残余拉应力最大值随着裂纹的扩展逐渐增加。在沿裂纹深度方向，残余拉应力最大值随着裂纹的扩展亦逐渐增加。

[1]Edwards L.Influence of residual stress redistribution of fatigue crack growth and damage tolerant design[J].Materials science forum，2006（524-525）：363-372.

[2]罗白璐.交变载荷下厚板表面焊接残余应力的松弛研究[D].湖北：武汉理工大学，2010.

[3]Chang D J，Ha C S，Young C J.Fatigue Life Assessment of Fillet Welded Joint Considering the Relaxation and Redistribution of Residual Stress[R].The 23rd International Conference on Offshore Mechanics and Arctic Engineering.Vancouver，British Columbia，Canada，2004：1-5.

[4]Barsoum a Z，Barsoum b L.Residual stress effects on fatigue life of welded structures using LEFM[J].Engineering Failure Analysis，2009，16（1）：449-467.

[5]杨化仁.疲劳裂纹扩展时焊接残余应力分布的测定[J].力学与实践，1994，16（2）：22-24.

[6]宋天明.残余应力的产生与消除[M].北京:中国石化出版社，2004.

[7]黄海.港口起重机金属结构安全性评价方法研究[D].武汉：武汉理工大学，2008：58-61.

[8]Pairs P，Endogan E A.Critical.Analysis of Crack Growth Laws[J].Journal of Basic Engineering Transaction of the ASME，1963（85）：528-534.

[9]徐晓丽.残余应力对焊接接头表面裂纹扩展的影响[D].辽宁：大连理工大学，2013.

[10]程书立.基于温度和应力场的焊接残余应力数值分析[D].南昌：南昌大学，2007.

[11]杨秉宪.微小裂纹的发生与扩展[J].北京航空学院学报，1984（2）：67-75.

[12]倪向贵，李新亮，王秀喜.疲劳裂纹扩展规律pairs公式的一般修正及应用[J].压力容器，2006，23（12）：8-19.

[13]孙文婷，万正权.对接焊残余应力的有限元分析[J].船舶力学，2007，11（1）：94-101.