焊接残余应力对矩形薄板力学性能影响
2015-03-12高永毅李学军邹声华
邹 曦 ,高永毅,李学军,邹声华
(1.湖南科技大学 机械设备健康维护省重点实验室,湖南 湘潭 411201;2.湖南科技大学能源与安全学院,湖南 湘潭411201)
0 前言
众所周知,金属构件在焊接过程中会产生残余应力。焊接残余应力的存在对构件的受力性能有很大的影响,如拉伸残余应力会降低疲劳强度和腐蚀抗力,压缩残余应力会提高金属材料的疲劳抗力。所以,对焊接残余应力的研究一直以来是国内外专家学者十分关注的研究课题,许多研究工作者做了很多有意义的工作,如:张定铨[1]等人研究了残余应力对金属疲劳强度的影响;周建新[2]研究了薄板焊接残余应力尺寸效应;卞如冈[3]等人定量研究了焊接残余应力对疲劳寿命的影响。目前,实际测量法和数值模拟法是研究焊接残余应力大小和分布的方法。研究表明,实际测量法的应用有一定的局限性,数值模拟方法可以模拟焊接过程,从而实现了对焊接过程应力场的分析。由此,很多研究工作者在数值模拟方面做了大量的工作,如:张国栋等人[4]对有残余应力的焊接接头的蠕变损伤行为进行了有限元模拟;闫德俊等人[5]利用有限元方法对平板TIG进行了数值模拟,分析了热物理参量对焊接残余应力峰值特征的影响。尽管这些模拟能再现焊接过程,也得出了一些有用的结论,但是目前这些有限元模型绝大多数是宏观模型,不能研究焊接残余应力在微观金属晶胞中的分布规律和外力在金属构件的分布受焊接残余应力的影响,也就不能从微观的角度来研究焊接残余应力对构件力学性能的影响。如果要从微观上来研究残余应力对构件力学性能的影响,就必须建立能反映真实微观结构的金属晶胞力学模型。因此,本研究参照金属晶胞结构,建立了金属多晶胞力学模型;利用该模型模拟了堆焊矩形薄板的焊接过程;得出了其残余应力的分布。并以此为基础,研究了残余应力对固有频率以及堆焊矩形薄板应力分布的影响。
1 金属多晶胞力学模型
1.1 模型的建立
1.1.1 单晶胞二维力学模型
以空间点阵为面心立方晶胞结构的金属为例,建立金属多晶胞力学模型。文献[6]给出了面心立方晶胞结构中在密排面上的原子排列,并指出若将每个原子简化成为一个质点,则在二维平面可以将单个晶胞简化为一个正六边形单元,如图1a所示,且每个原子和相邻最近的原子之间都是相切的,如图1b所示。文献[7]在文献[6]的基础上假设晶体材料是连续和均匀的。根据文献[6]与文献[7]给出的结论,可以忽略原子之间的空隙,在x-y平面建立起图2所示的单晶胞二维力学模型,该模型为一正六边形平面。由于铝的空间点阵是面心立方晶胞结构,所以以铝为母板材料,其六边形边长取铝的晶格常数,即:a=4×10-6。
1.1.2 二维多晶胞力学模型
在单晶胞二维力学模型的基础上,将多个单晶胞力学模型按图1a的规则排列建立如图3所示的二维多晶胞力学模型。该模型由76个单晶胞模型组成,中间为平行y轴沿轴线的焊缝区,取焊缝区焊接材料与母板材料相同,其焊接方式为堆焊方式。由文献[6]进一步指出,原子密排面在空间的排列情况完全相同,三维晶胞结构是由密排面上的原子在空间一层一层平行“堆砌”起来的,每层的性质完全相同,因此,可以先研究二维情况,为以后三维情况的研究打下基础。

图1 面心立方晶胞结构密排面上的原子排列Fig.1 Arrang ement of atoms on the close-packed plane of face-centered cubic lattice structure

图2 二维单晶胞力学模型Fig.2 Single cell mechanical model
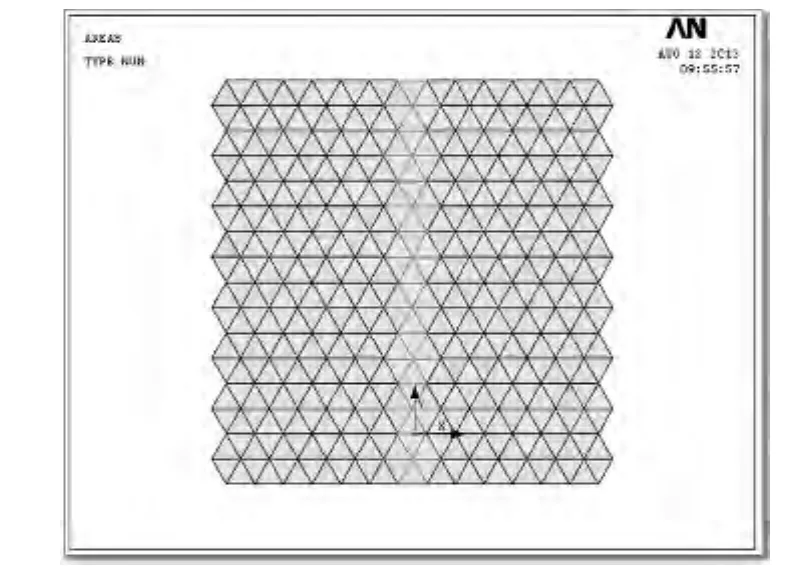
图3 二维金属多晶胞力学模型Fig.3 Two-dimensional micro metal lattice model
1.2 模型参数的确定
由于是以铝为母板和焊缝区焊接材料,所以以铝的材料参数为模型参数,铝的材料参数如表1所示。
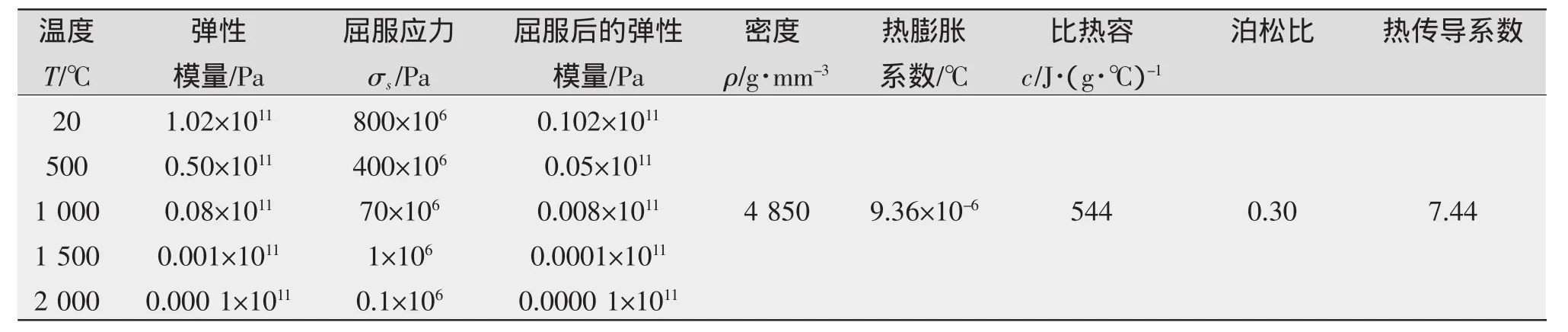
表1 铝的材料参数Tab.1 Parameters of aluminium
1.3 网格划分及约束
为了利用该模型模拟焊接时的二维温度场及残余应力场分布,热分析单元选取shell157。为了保证计算精度,在焊缝区及近焊缝区细化网格,而远离焊缝区则采用较粗的网格。对晶胞两边16个节点进行全约束,网格划分及约束情况如图4所示。
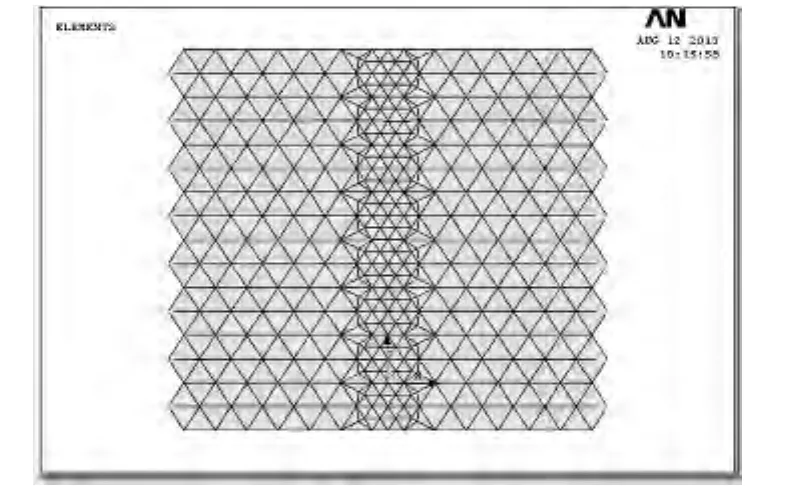
图4 网格划分及约束Fig.4 Mesh and constraints
2 焊接残余应力模拟
焊接是一个局部快速加热到高温,并随后快速冷却的过程,材料的热物理性能也随温度剧烈变化。焊接加热产生的不均匀温度场和造成材料的相变,以及焊件受外界约束而产生的附加应力是产生焊接残余应力的因素;但文献[8]明确指出,在这些因素中,焊接残余应力产生的主要因素是由于焊接加热产生的不均匀温度场引起的;由于不均匀温度场使得材料内部存在温度梯度,温度梯度造成了材料的不均匀加热或冷却,也就使材料内部出现了不均匀的热胀冷缩现象,从而产生了材料内部的热应力。因此焊接残余应力主要是热应力。
2.1 热源模拟
对金属进行堆焊过程模拟时,首先设置焊料的初始温度为1 500℃,模型左右边界温度20℃,假定无对流和辐射。然后可采用生死单元技术通过模拟焊缝填充来模拟焊接热源输入过程[9],即将全部焊接热量均匀分布在焊缝上。在开始计算前,将焊缝中所有单元“杀死”,在计算过程中,按顺序将被“杀死”的单元“激活”,模拟焊缝金属的填充。
2.2 焊接残余应力分布
利用ANSYS软件和以上所建立的金属多晶胞模型,对矩形薄板堆焊过程进行模拟,通过热分析计算得出相应的节点温度场数据,然后代入应力场分析中,得知矩形薄板焊后残余应力分布,如图5所示。由图5可知,最大残余应力分布在焊缝中心单元处,达到0.119×104MPa,焊缝单元处的残余应力在 0.55×103~0.119×104MPa;残余应力总体来说呈对称分布,由焊缝单元向两边单元逐级递减,最小应力为37 MPa。
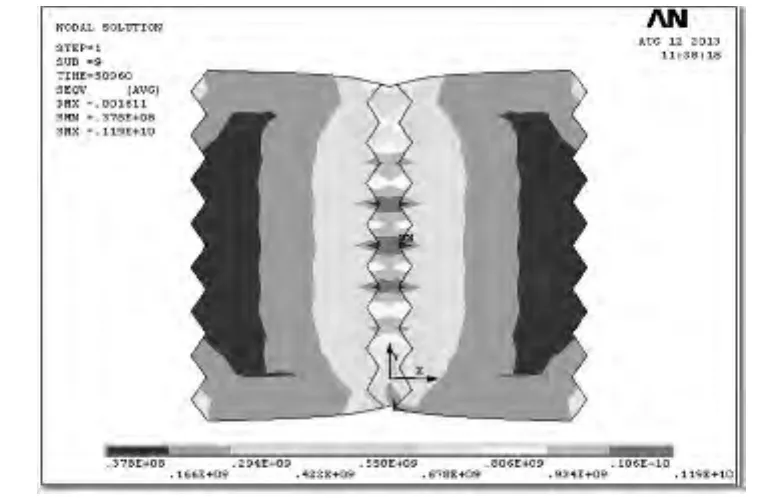
图5 焊后残余应力分布Fig.5 Distribution of residual stress
3 焊接残余应力对矩形薄板力学性能影响及模型的验证
由于焊接残余应力主要是热应力,是焊接加热产生的不均匀温度场引起的;因此在研究焊接残余应力对矩形薄板力学性能的影响时,只考虑由于不均匀温度场引起的热应力;而不考虑焊后相变等情况。
利用ANSYS软件和建立的金属多晶胞模型,研究残余应力对矩形薄板固有频率的影响。表2为计算得出的焊前无焊接残余应力与焊后有焊接残余应力矩形薄板前10阶固有频率以及对比情况。由表2可知,在焊后有残余应力存在的情况下,矩形薄板各阶固有频率与焊前无焊接残余应力时相比都有所增加,且高阶固有频率比低阶固有频率受残余应力影响更大。

表2 焊前焊后模型模态及对比结果Tab.2 Mode of the model before and after welding and results
3.2 试验验证
试验选用了如图6所示的矩形薄板试件。试件的尺寸为1 000 mm×100 mm×4 mm,对图7所示的矩形薄板试件进行了焊接前后固有频率测量的对比试验,试验结果如表3所示。
图6 矩形薄板试件Fig.6 Rectangular thin plate specimen

表3 图7所示矩形薄板残余应力测量结果Tab.3 As shown in Fig.7 rectangular thin plate residual stress measurement results
表3得出的结论与表2中的结论相符合,即有焊接残余应力存在时,构件的各阶固有频率增加。且在其他因素不变时,高阶频率受残余应力的影响比低阶频率大,随着阶数的增加,频率变化增大,说明使用该模型模拟研究分析焊接残余应力对矩形薄板力学性能影响是正确的。
3.3 对矩形薄板内应力的影响
利用ANSYS软件和以上所建立的金属多晶胞模型,研究残余应力对矩形薄板在外力作用下的应力分布及大小的影响。
3.3.1 对矩形薄板内应力分布的影响
由图5可知,在焊缝灰色区域残余应力最大,因此在残余应力最大节点处,即:第120节点处施加外力,如图7所示,外力方向垂直于模型向下,大小为:F=0.01 MPa。计算得出的矩形薄板内部应力分布结果如图8所示,其中图8a、图8b分别为焊接前后在矩形薄板多晶胞模型上施加外力时的应力分布。比较图8a、图8b可知,焊接前后矩形薄板晶胞间的应力分布规律基本一致,且呈对称分布。因此,残余应力对矩形薄板内应力分布的影响不大。
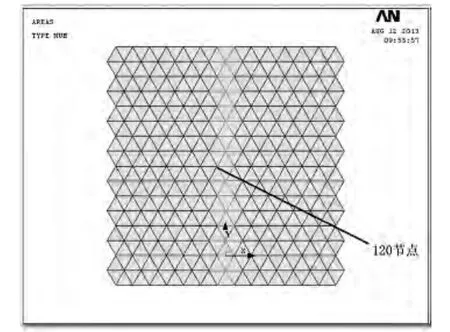
图7 晶胞模型受外力示意Fig.7 Schematic diagram of force by the cell model
3.3.2 对矩形薄板内应力大小的影响
(1)晶胞中原子上应力的大小。
计算矩形薄板内处于不同区域的晶胞中各个原子上的应力大小,其结果如表4所示。表4给出了焊接前后矩形薄板在如图6所示的外力作用下,在焊缝区的1号晶胞中处于第98、114节点上的原子的应力值;2号晶胞中处于第55、35节点上的原子的应力值;3号晶胞中处于第166、167节点上的原子的应力值。在近焊缝区的4号晶胞中处于第206、213节点上的原子的应力值;5号晶胞中处于第170、285节点上的原子的应力值。在远离焊缝区的6号晶胞中处于第71、54节点上的原子的应力值;7号晶胞中处于第266、186节点上的原子的应力值;8号晶胞中处于第138、140节点上的原子的应力值。其晶胞号和节点号如图9所示。

图8 焊接前后对矩形薄板施加外力后的应力分布Fig.8 Stress distribution after applied the external force before and after welding on a rectangular plate

图9 晶胞号及节点号示意Fig.9 Schematic diagram of cell number and node number
由表4可知,不管在矩形薄板内哪个区域,施加外力后,无焊接残余应力时晶胞中原子的应力值均比有焊接残余应力时的应力值要小。
(2)晶胞中原子间金属键上应力的大小。
计算矩形薄板内原子间金属键应力大小,其结果见表5。表5给出了焊接前后矩形薄板在如图6所示的外力作用下,在焊缝区的1号晶胞中第1、2号金属键上的应力值;2号晶胞中第3、4号金属键上的应力值。在近焊缝区4号晶胞中第5、6号金属键上的应力值;5号晶胞中第7、8号金属键上的应力值。在远离焊缝区6号晶胞中第9、10号金属键上的应力值;8号晶胞中第11、12号金属键上的应力值。其晶胞号和金属键号如图10所示。由表5可知,不管在矩形薄板内哪个区域,施加外力后,无焊接残余应力时晶胞中原子间金属键上的应力值比有焊接残余应力时的应力值小。
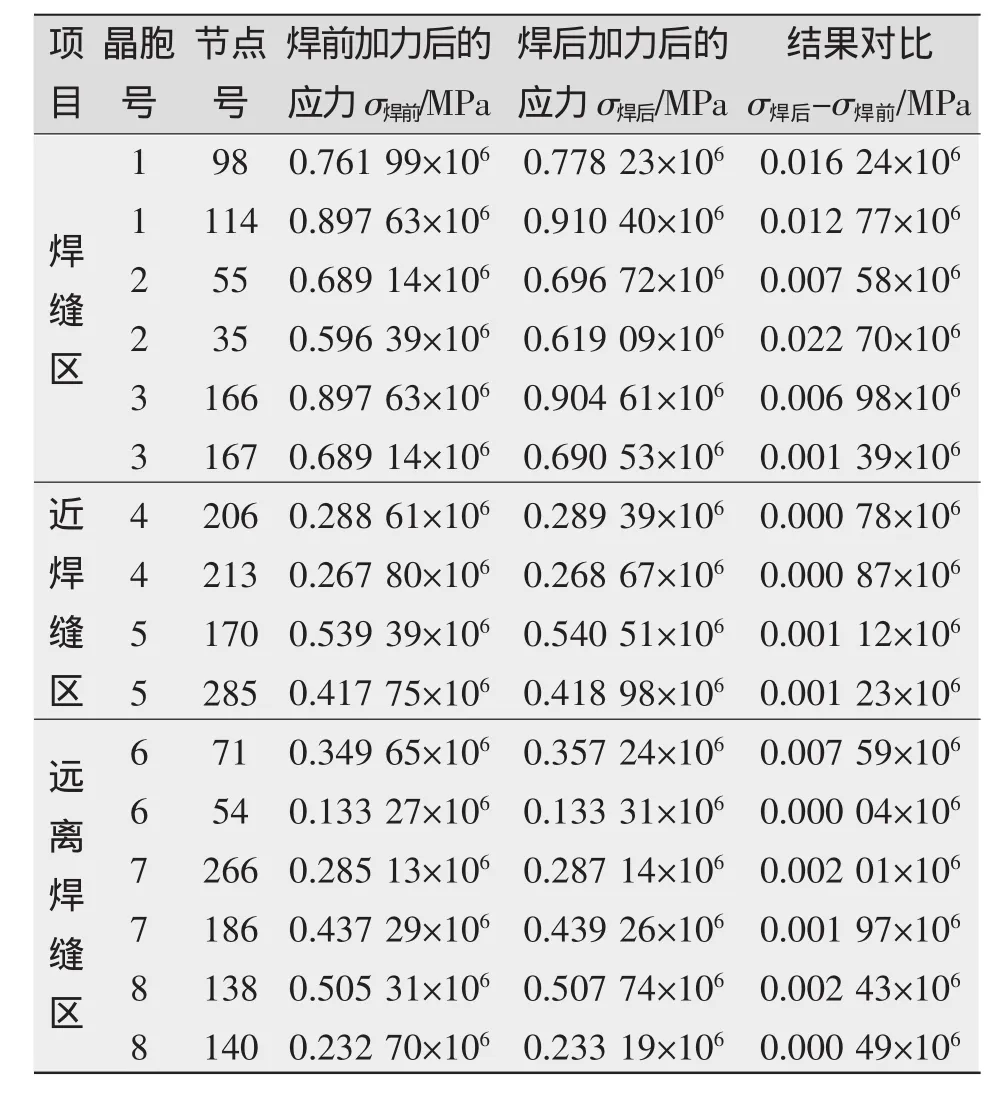
表4 焊接前后晶胞间原子应力大小及对比Tab.4 Atoms'stress and contrast between cell before and after welding

表5 焊接前后原子间金属键应力大小及对比Tab.5 Atomic metal bonds'stress and contrast before and after welding

图10 晶胞号和金属键号示意Fig.10 Schematic diagram of cell number and metal bond
4 结论
(1)提供了一种从微观角度来模拟矩形薄板焊接残余应力的方法,为研究焊后如何消除残余应力,提高焊件的稳定性提供指导。
(2)有焊接残余应力存在时,薄板的各阶固有频率增加,且高阶固有频率比低阶固有频率受残余应力影响较大。
(3)残余应力对在外力作用下的矩形薄板的应力分布规律基本没有影响,只对其应力分布大小有影响。
(4)施加外力后,在矩形薄板内,无焊接残余应力时晶胞中原子上的应力值比有焊接残余应力时的应力值小。
(5)施加外力后,在矩形薄板内,无焊接残余应力时原子间金属键上的应力值比有焊接残余应力时的应力值小。
[1]张定铨.残余应力对金属疲劳强度的影响[J].理化检验-物理分册,2002,38(6):231-235.
[2]周建新,徐宏,王俊胜,等.薄板焊接残余应力尺寸效应[J].焊接学报,2006,27(3):96-100.
[3]卞如冈,崔维成,万正权,等.焊接残余应力对疲劳寿命影响的定量研究[J].船舶力学,2011,15(7):776-783.
[4]张国栋,周昌玉.焊接接头残余应力及蠕变损伤的有限元模拟[J].金属学报,2008,44(7):848-852.
[5]闫德俊,刘雪松,杨建国,等.有限元分析热物理参量对焊接残余应力峰值特征的影响[J].焊接学报.2010,31(6):56-60.
[6]胡赓祥.材料科学基础(第二版)[M].上海:上海交通大学出版社,2006.
[7]曾有良.晶体材料力学性能的热力学微观机理及本构方程的研究[J].华东理工大学学报.2000,26(4):396-400.
[8]宋天民.焊接残余应力的产生与消除(第2版)[M].北京:中国石化出版社,2010.
[9]高明宝,李世芸,邹云鹤.运用ANSYS对焊缝残余应力及温度场分析[J].科学技术与工程,2011,11(1):159-162.
