新型混合励磁双凸极电机非线性磁网络分析

孙 莉，张振华，丰树帅，张卓然

(1.中国船舶重工集团公司第七〇四研究所，上海200031;2.南京航空航天大学，南京210016)

0 引 言

双凸极永磁电机(以下简称DSPM)的本质是一种定子上有永磁体的可变磁阻电机。它有着磁阻电机结构简单牢固和永磁电机功率密度高［1-3］的优点。但永磁体的存在使其弱磁调速和发电电压调节困难，并且由于稀土永磁材料的价格不断增长，引起了DSPM 的成本大幅提高;电励磁双凸极电机(以下简称DSEM)磁场调节方便［4-6］，但励磁绕组的存在使DSEM 的功率密度和效率都相对较低。

混合励磁双凸极电机(以下简称HEDSM)综合了DSPM 和DSEM 的优势，在永磁磁势源产生主磁场的同时，辅以可变的电励磁磁势源，实现对电机主气隙磁场的宽范围调节。HEDSM 不仅继承了DSPM 的众多优点，而且具有DSEM 气隙磁场平滑可调的特点。文献［7 -8］研究了一种由共轴的DSPM 和DSEM 组成的并列结构的HEDSM。该结构下的DSPM 与DSEM 的磁路是相互独立的。文献［9 -10］分析了一种含有导磁桥的HEDSM，合理选取导磁桥的尺寸，能达到用较小的直流励磁磁势获得较大的气隙磁通调节范围的目的［11］。

磁链、电感等静态特性参数是新型HEDSM 设计、研究的基础。由于HEDSM 存在明显的局部饱和和非线性，求解上述参数比较困难。通过有限元法(通常借助于有限元商用软件如ANSYS，Ansoft等)可以较为准确地求解这些参数，但有限元计算往往耗时较长，计算效率较低，难以快速获取不同状态下的电机特性参数。等效磁网络的概念于20 世纪60 年代提出［12］，基于磁网络的磁路计算方法已成功应用于永磁同步电机［13］、爪极电机［14］磁阻电机［15-17］等电机的磁场计算。

本文针对新型HEDSM，建立其不同转子位置角下的等效磁网络模型，分析各部分等效磁导，并引入和推导磁导修正系数，为新型HEDSM 的快速准确设计和静态特性分析奠定基础。

1 混合励磁双凸极电机结构原理

图1 为新型24/16 极HEDSM 结构图。与传统DSPM，DSEM 类似，HEDSM 定子、转子结构均是凸极的。与DSEM 相似，定子槽内嵌绕电枢绕组和励磁绕组，均为集中式绕组;与DSPM 相似，将永磁体嵌入于定子轭部。永磁体和励磁绕组共同作用形成混合励磁结构［18-19］。因此，HEDSM 存在两种励磁源:永磁磁势源和电励磁磁势源，二者相互作用，形成电机主磁场。当励磁绕组通入直流励磁电流时，产生的直流励磁磁势与永磁磁势呈并联关系。

图1 24/16 极混合励磁双凸极电机结构示意图

根据定子极上的电枢绕组中匝链的磁通变化规律，可将电枢绕组构成一套或多套三相绕组。图2是HEDSM 的三套电枢绕组和励磁绕组的连接示意图。A1，B1，C1相电枢绕组的磁链主要由永磁磁势决定;A2，B2，C2相电枢绕组的磁链由永磁磁势和直流励磁磁势共同决定;A3，B3，C3相电枢绕组的磁链主要由励磁磁势决定。将三套电枢绕组依次串联可形成一套电枢绕组。

通常励磁绕组中通入的直流电由单独的永磁励磁机提供。但是由于永磁体磁阻较大，A1，B1，C1相电枢绕组磁链受直流励磁磁势影响较小，因而可经整流后作直流励磁源，为HEDSM 提供励磁功率，从而运行于独立工作状态。

2 等效磁网络模型

2.1 等效磁网络模型的建立

等效磁网络模型是根据等效磁通管原理，将磁通分布比较均匀、形状又比较规则的部分当作一个单元，计算场域内所有单元的等效磁导并将其通过节点连接形成等效磁网络模型。因此根据图3 中HEDSM 的磁通路径可将HEDSM 主要可分成6 个单元:定子轭;定子极;相邻定子极间气隙;定、转子间气隙;转子极;转子轭。定义图1 中转子位置角θ为0°。图3 是转子位置角为0°和3.75°时HEDSM 1/4 部分的磁链走向图，根据磁链走向以及磁通路径划分情况，图4 是对应的等效磁网络模型。其中，FI，FPM分别指等效永磁磁势和励磁磁势Gg和G0分别表示永磁等效磁导、和漏磁导(通过定子轭);Gps，Gys分别为定子极和定子轭磁导，其中定子极分为上下两部分，分别为Gps_1和Gps_2;Gpl和Ga分别表示相邻定子极间漏磁导和定子和转子极之间的气隙磁导;Gpr，Gyr分别为转子极和转子轭的磁导。

2.2 参数计算

等效励磁磁势FI为励磁电流If和励磁绕组匝数Nf的乘积:

等效永磁磁势FPM与永磁材料剩磁Br、永磁体厚度hPM有关，计算公式:

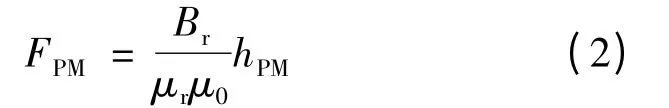
式中:μr，μ0f分别指永磁体相对磁导率和真空磁导率。

Gps，Gpr，Gys和Gyr为铁心磁导，其值是关于铁心磁导率的非线性函数，可根据铁磁材料的磁导计算:

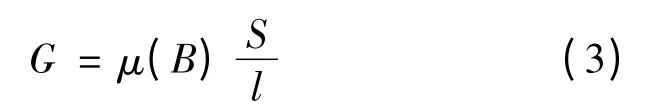
式中:μ(B)为铁磁材料的磁导率，其值与磁感应强度B 相关;S 为磁通通过部分的截面积;l 为磁通通过路径的长度。

永磁体等效磁导Gg:

式中:lPM是永磁体高度;la是铁心长度。

Ga和Gpl为气隙磁导，是线性函数，Gpl为常量，而Ga的值随转子位置变化而变化。Ga是磁路模型的关键参数，对模型的精确性有很大的影响。基于如下假设，进行气隙磁导的分析计算［15］:(1)磁场分布在轴向，是均匀的，且铁磁材料具有无穷大的磁导率;(2)定子和转子的铁心表面磁位处处相等且与磁力线相互垂直;(4)当定子与转子极夹角大于1/2定子极弧(3.75°)时，可忽略其磁通路径，从而忽略其气隙磁导。图5 为定、转子结构展开图(转子位置角θ=α)。

图5 θ=α 时定、转子结构展开图

因此，HEDSM 在不同转子位置的气隙磁通路径可以分成4 种典型情况:1)定子极与转子极部分重合(转子极A 与定子极A 间);2)定子极与转子极完全分开，但两者夹角小于3.75°(转子极A 与定子极B 的气隙磁通路径);3)定子极与转子极完全分开，但两者夹角大于3.75°(转子极B 与定子极B 的气隙磁通路径);4)定子极与转子极完全重合。因此由于第三种情况忽略气隙磁导，其他3 种典型的气隙磁导计算公式［15-16］:

式中:μ0为真空磁导率;l 表示实际铁心长度;g 表示气隙长度;r 表示转子极弧半径;θ 表示与定子极完全重合的转子极转过的角度。

2.3 磁导修正系数kc

由于计算气隙磁导时定义了假设条件，因此气隙磁导的计算结果存在误差。而气隙磁导的计算对整体计算影响较大，为了克服该误差，提高计算结果的精确性，在有限元计算结果的基础上引入磁导修正系数kc［15］:

其中系数c1和c2可以通过有限元仿真法计算两个特殊位置的气隙磁导得出。气隙磁导经修正如式(8):

图6 定转子极部分重叠时磁场分布示意图

如图6 所示，当转子极和定子极存在重叠部分时，由于定、转子极近气隙处磁场强度不均匀，导致磁路长度变大且不与铁心表面垂直。故若简单的根据尺寸计算，其磁导值计算结果将偏大。以下考虑磁场分布不均匀对定子极磁导计算的影响:将定子极磁导根据磁链走向分成定子极上半部和定子极下半部。定子极上半部磁力线可近似认为直线，按式(2)计算，定子极下半部的磁导计算是在定子极上半部的基础上进行修正。根据图7(b)和图7(c)，当θ 为3.75°时，定子极下半部的磁通路径与极身的夹角近似为22.5°;当θ 为7.5°时，其夹角约为45°。因此定义了定子极下半部分的磁导修正系数ks:

同样如图6 所示，转子极磁通路径较短，但大致走向与定子极类似，因此，转子极磁导可用定子极磁导的计算方法类似推导。

等效磁网络模型是随着转子位置角的变化而变化的，由于HEDSM 的定子不动，以及转子的对称性，HEDSM 在转子不同位置时的等效磁路模型与图4 相比，仅仅是气隙磁导值的变化而已。

2.4 模型的求解

根据电网络中的回路磁通法，列写磁网络方程得:

式中:Rm为磁阻矩阵，磁阻是以上计算的磁导的倒数;Φ 为磁通向量;F 为磁势向量。其中Rm向量中，除气隙磁导是关于转子位置角的函数，其他都为常数。当转子位置固定时，气隙磁导也为常数。F向量中包括励磁磁势和永磁磁势。铁磁材料的磁导率是磁感应强度B 的非线性函数，通过其B -H 曲线可得:

给定Φ 的初值和迭代精度ε(ε ＞0)，采用牛顿法求解式(12)。通过循环迭代得到Φ 值，当相邻两次所得的Φ 值满足:

即认为迭代结束。在求解过程中，引入系数λ(0≤λ ＜1)来表征上次计算结果对本次结果的影响［20］:

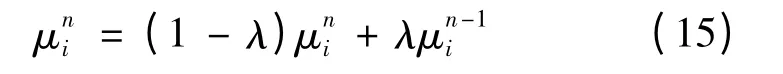
3 计算结果与仿真实验验证

本文以表1 的新型24/16 极HEDSM 样机为例进行讨论。当转子转过一圈，磁链变化16 次，即电机极对数等于转子极数(Nr)。因此24/16 极HEDSM 的一个电周期:

由于忽略定、转子极间夹角大于1/2 定子极弧(3.75°)时的气隙磁导，因此半个周期的磁网络分别为0° ～3.75°和3.75° ～11.25°的磁网络模型，如图4(a)、图4(b)所示。在这两个区间范围内以一定步长求解网络方程，并在角度和结构上进行拓展，即可获得整个HEDSM 在整个电周期的磁链曲线，进而得到感应电势波形。

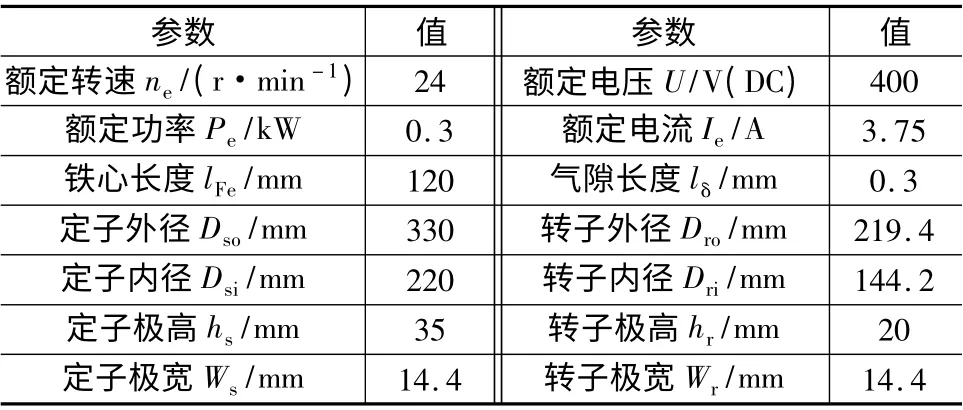
表1 样机结构参数

表2 表示励磁电流为5 A 时分别采用磁网络法以及有限元法得到HEDSM 的A1相磁链值比较，由表2 可得两者结果相近，表明磁网络法计算电机磁链具有较好的计算精度。

表2 有限元与磁网络法磁链计算结果比较

图8 为分别采用磁网络法和有限元法计算得到的磁链波形图，两者基本吻合。在磁链最小值处存在一定误差的原因，可能是:(1)忽略了定子轭与定子极上半部之间的漏磁导;(2)气隙磁导计算时，电机旋转区间划分较大，且忽略了定子极与转子极的夹角大于1/2 定子极弧时的气隙磁导;(3)忽略了定子极与转子极有部分重叠时，极尖局部饱和情况以及饱和对气隙计算带来的影响。

HEDSM 感应电势:

式中:e 为电枢感应电势;ψ 为磁链;ω 为转子角速度。

图9 是采用磁网络法和有限元法所得的相电势波形图，图10 是相应的实验结果。由两者的波形对比可得两种计算方法的结果基本是一致的，其中电势波形的尖峰主要由计算中电机不同位置点磁链误差的不均匀性而引起。实验结果进一步验证了非线性磁网络分析的准确和有效性。

4 结 语

本文阐述了一种新型混合励磁双凸极电机的结构及其原理，并依据不同的转子位置角建立等效磁网络模型，从而得到该电机定子、转子等部分的计算磁导的方法。引入气隙磁导修正系数，并考虑了定转子极部分重叠时局部饱和对定子极磁导计算的影响，推导了定子极磁导修正系数。通过非线性磁网络分析计算，得到了电机不同励磁电流下的绕组磁链和感应电势。1.5 kW 混合励磁双凸极电机的有限元计算结果与磁网络分析一致，且原理样机的实验结果进一步验证了磁网络模型的正确性，表明所建立的非线性磁网络模型可以快速而准确地计算新型混合励磁双凸极电机的静态磁场分布和输出特性，为该新型混合励磁双凸极电机的快速设计和结构优化提供了有效分析手段。

［1］ LIAO Y，LIANG F，LIPO T A. A novel permanent magnet motor with doubly salient structure［J］. IEEE Transactions on Industrial and Application，1995，31(5):1069 -1078.

［2］ 孟小利，严仰光.双凸极永磁电机的发展及现状［J］.南京航空航天大学学报，1999，31(3):330 -335.

［3］ LIU C，CHAU K T，JIANG J Z，et al.Comparison of stator - permanent - magnet brushless machines［J］. IEEE Transactions on Magnetics，2008，44(11):4405 -4408.

［4］ CHAU K T，CHENG Ming，CHAN C C.Nonlinear magnetic circuit analysis for a novel stator doubly fed doubly salient machine［J］.IEEE Transactions on Magnetics，2002，38(5):2382 -2384.

［5］ 陈冉，陈志辉，毛志鑫，等.一种用于电励磁双凸极发电机的新型半控整流拓扑研究［J］. 电机工程学报，2012，32(36):117-122.

［6］ 朱德明，邱鑫，张卓然，等.直驱式电励磁双凸极风力发电机的极数研究［J］.电机工程学报，2009，29(18):65 -70.

［7］ CHEN Z H，SUN Y P，YAN Y G.Static Characteristics of a Novel Hybrid Excitation Doubly Salient Machine［C］//Proc. of International Conference on Electric Machines and Drives (ICEMS05)，Nanjing，China，2005:718 -721.

［8］ 秦海鸿.混合励磁双凸极电机的基本特性研究［D］. 南京:南京航空航天大学，2006.

［9］ ZHU X Y，CHENG M.A novel stator hybrid excited doubly salient permanent magnet brushless machine for electric vehicles［C］//Proc. of International Conference on Electric Machines and Drives(ICEMS05)，Nanjing，China，2005:412 -415.

［10］ ZHU X，CHENG M，HUA W，et al.Design and analysis of a new hybrid excited doubly salient permanent magnet machine capable of field control［C］//IEEE Industry Application Society Annual Meeting，Tampa，USA，2006:2382 -2389.

［11］ 朱孝勇，程明，赵文祥，等. 混合励磁电机技术综述与发展展望［J］.电工技术学报，2008，23(1):30 -39.

［12］ LAITHWAITE E R.Magnetic equivalent circuits for electric machines［C］//Proc. of Institution of Electrical Engineers (IEE)，1967，114(11):1806 -1809.

［13］ 周洁，谢卫，汪国梁.用等效磁网络法与有限元法计算永磁电机参数的比较［J］.西安交通大学学报，1998，32(4):23 -26.

［14］ 乔东伟，王秀和，朱常青.基于等效磁网络法的新型混合励磁无刷爪极发电机的性能计算［J］. 电机与控制学报，2012，16(11):23 -26.

［15］ CHENG Ming，CHAU K T，CHAN C C，et al.Nonlinear varyingnetwork magnetic circuit analysis for doubly salient permanentmagnet motors［J］. IEEE Transactions on Magnetics，2000，36(1):339 -348.

［16］ ZHU Z Q，PANG Y，HOWE S，et al. Analysis of electromagnetic performance of flux - switching permanent magnet machines by non - linear adaptive lumped parameter magnetic circuit model［J］. IEEE Transactions on Magnetics，2005，41(11):4277 -4287.

［17］ ZHANG Gan，CHENG Ming，HUA Wei. Analysis of flux -switching permanent-magnet machine by nonlinear magnetic network model with bypass-bridges［C］//Proc. of International Conference on Electric Machines and Systems (ICEMS 2010)，Inchon，Korea，2010:1787 -1791.

［18］ 陶洋洋.新型混合励磁双凸极无刷直流发电机基本特性研究［D］. 南京:南京航空航天大学，2012.

［19］ ZHANG Zhuoran，TAO Yangyang，YAN Yangguang. Investigation of a new topology of hybrid excitation doubly salient brushless DC generator［J］.IEEE Transactions on Industrial Electronics，2012，59(6):2550 -2556.

［20］ 程明，王运良，叶炬.集中绕组外转子永磁同步发电机非线性变网络磁路分析［J］.东南大学学报(自然科学版)，2006，36(2):252 -256.