直线压缩机磁路分析方法的研究

李志海

(广东石油化工学院，茂名525000)

0 引 言

直线压缩机是一种高效冰箱压缩机，LG 直线压缩机的效率比现有最高效压缩机的效率高20% ～30%，其电机效率可达95%［1］。研究直线压缩机的设计和应用具有重要的节能效益，目前针对直线压缩机的结构设计和控制有比较多的研究［2-6］。

直线压缩机的电磁系统包括由永磁体、铁心以及内外轭铁间气隙组成的磁路和线圈与外接电源组成的电路系统。动磁式直线压缩机的内轭铁结构如图1 所示，动圈式直线压缩机磁路结构如图2 所示。从图中可以看出磁路中都有部分磁路硅钢片不是严密叠加在一起，而是硅钢片之间存在气隙。传统磁路分析方法有等效电路法［7］，将磁路用电路等效代替，使用欧姆定律计算。该方法不能确定磁路中具体的磁通分布。另一种设计方法是有限元法［8-9］，但是针对图1 和图2 所示的结构，二维建模分析时无法考虑硅钢片间的间隙对磁通的影响，而如果采用三维模型，硅钢片厚度以及硅钢片间气隙宽度比其他方向尺寸小很多，为分析硅钢片间气隙的影响，需对该区域进行网格细化，使得整个有限元模型网格数量庞大，计算时间较长，需要内存较大，同时由于气隙处网格的畸形甚至可导致计算不收敛。

图1 动磁式直线压缩机的内轭铁结构

图2 动圈式直线压缩机磁路结构

本文通过研究建立了一种适应这种磁路结构的新的磁路分析方法，既考虑磁路结构中硅钢片间气隙的影响，又能准确反映整个磁路的磁通分布，为磁路的设计优化提供一种新的方法。

1 系统模型

图3 为本文的动圈式直线压缩机磁路结构示意图。该直线压缩机磁路系统包括内轭铁、外轭铁、下轭铁、永磁体和线圈(如图6 所示)。内轭铁内部装有气缸，外轭铁在内轭铁的外部，并与内轭铁之间形成一个气隙。内、外轭铁都是由硅钢片叠加在一起，形成圆柱结构，在圆柱外端硅钢片间存在狭小气隙。线圈缠绕在线圈支架上，线圈支架插入内、外轭铁形成的气隙中。

图3 磁路结构示意图

当位于磁场中的线圈通有交流电时，线圈中将产生往复激励力，推动与其固定在一起的活塞作往复运动。另外周期性变化的电流将在铁心中引起磁场周期性变化，产生涡流损耗。为减少涡流的影响，磁路通常由磁性材料的薄叠片做成，如图1 ～图3所示。这些叠片沿磁力线方向排列，相互之间由其表面的氧化层或者绝缘涂层来绝缘，从而切断涡流路径，减小涡流损耗。

本文中铁心材料采用一种典型铁磁材料50TW470 硅钢片，其B-H 特性曲线如图4 所示，其相对磁导率与磁感应强度的关系曲线如图5 所示。

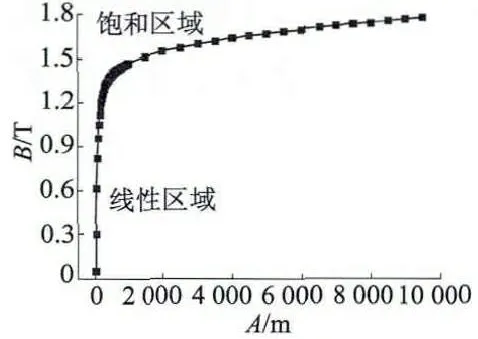
图4 50TW470 硅钢片的B-H 特性曲线

图5 50TW470 硅钢片相对磁导率与磁感应强度的关系

磁路结构分析模型如图6 所示。根据磁路特点和磁力线不相交，作如下假设:(1)磁力线在铁心内部分层分布，即磁力线根据铁心的宽度分布，里面磁力线始终位于内部，外面磁力线走大圈;(2)磁力线转弯处直角转弯;(3)永磁铁的磁通全部导入气隙中。由此可得磁力线路线如图6 中黑粗线所示，路径分为1 到11 部分。

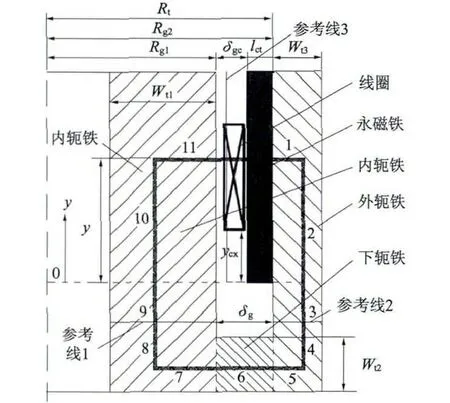
图6 磁路结构分析模型示意图

取其中的第i 层进行分析(如图6 中的阴影)，将整个磁路环线分成11 个部分。根据磁阻计算公式，图中第11 部分的磁阻:

式中:Ri11为铁心内轭铁中第i 层磁路中的第11 部分磁阻;Aniry为铁心内轭铁中第i 层磁路中的第11部分横截面积。第11 部分整个面积是一个圆柱，磁力线垂直圆柱面穿过。该面积是指该区域磁力线穿过的铁心横截面积，不包括硅钢片间气隙面积。假定硅钢片在半径Rgn=Rg1-Wt1处紧密排列，没有间隙。Aniry也可以按照公式Aniry=nggptggpδy计算，其中nggp为内轭铁中硅钢片的数量，tggp为每一块硅钢片的厚度。μFe为铁心材料的相对磁导率;Rnδyip为在铁心内轭铁中第i 层磁路中的内圆半径。

式中:δnk为铁心内轭铁中第k 层的宽度。

为了将计算结果同有限元分析的结果进行比较，假定硅钢片间没有狭小气隙，整个圆柱都为硅钢片材料组成。此时第11 部分的磁阻如下:

同理可得1、2 -4、5 -7 和8 -10 部分的磁阻。所以铁心第i 层磁路的总磁阻:

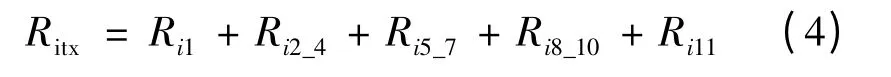
式中:Ritx为铁心第i 层磁路的总磁阻。

将所有层的磁阻相加，可得整个铁心的磁阻:

式中:Rtxt为整个铁心磁路磁阻。

如果δni，δxi，δwi取不同的值，得到整个铁心磁路的磁阻也不相同。因各层的磁力线穿过铁心总是走磁阻最小的方向，可建立以各层磁路宽度为设计变量、总磁阻最小为目标函数的优化设计模型。

通过优化函数，求解式(6)可得到内轭铁、外轭铁和下轭铁各层的宽度，从而可以求得铁心中各层磁路的磁阻。

为确定气隙的磁通分布和磁感应强度，还需要确定气隙的磁阻，以及计算永磁体和线圈产生的磁势。

第i 层磁路中气隙的磁阻:

式中:Rigas为第i 层磁路中的气隙磁阻。

第i 层磁路中铁心和气隙产生的磁势降:

式中:(Hl)itx为第i 层磁路中铁心产生的磁势降;(Hl)igas第i 层磁路中气隙产生的磁势降;Δφi为通过第i 层磁路中的磁通。

永磁铁是磁势源，它将提升整个磁路的磁势，根据永磁铁退磁曲线，可得到永磁铁中磁感应强度与磁场强度的关系，进一步可以得到永磁铁的磁势降:

式中:Bim为第i 层磁路中永磁铁处的磁感应强度;(Hl)im为第i 层磁路中永磁铁的磁势降。

对第i 层磁路来说:

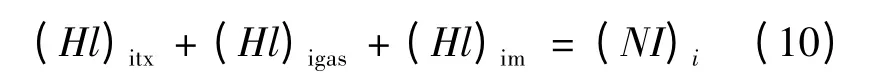
式中:(NI)i为第i 层磁路里面所包含的总电流数，正负号由安培右手定则确定。

将各部分的磁势降代入式(10)，可以求得各层磁路中通过的磁通Δφi，从而求得磁路各处的磁感应强度。如铁心在第i 层磁路中第11 部分的磁感应强度:

式中:Bi11为第i 层磁路中第11 部分的磁感应强度。

2 结果验证

为了验证磁路分析模型的正确性，将其结果与有限元结果进行比较分析。因有限元模型不能分析硅钢片间存在气隙的情况，所以验证模型中假定气隙全部充满硅钢片。在磁导率为常数时内轭铁、外轭铁的磁感应强度如图7、图8 所示。图中内轭铁的磁感应强度是指图6 中参考线1 处沿y 方向的磁感应强度(下同)，图中外轭铁的磁感应强度是选择图6 中参考线2 处沿y 方向的磁感应强度(下同)。从两图中可以看出，两种方法的分析结果基本一致。靠近气隙处(气隙位于半径从41 ～53 mm 处，下同)的磁感应强度比远离气隙的磁感应强度大，因为靠近气隙的这一层磁路路径短、磁阻小，从而磁感应强度大。

图7 铁心磁导率为常数时内轭铁的磁感应强度

图8 铁心磁导率为常数时外轭铁的磁感应强度

铁心材料的相对磁导率通常是随磁场强度变化而变化的，如图5 所示。此时磁路分析时需要进行迭代计算。首先假设一个初始相对磁导率，求出各层的磁阻和磁通，再通过式(11)求出各处的磁感应强度，通过图5 可以得到各处的相对磁导率。然后将得到的相对磁导率代入磁阻公式重新求磁阻，再得到磁感应强度，这样一直迭代下去，直到各处磁阻不变，以及磁路总磁阻最小为止。

计算的几何模型与在磁导率为常数时的模型一致，铁心材料性能如图4、图5 所示。计算得到内轭铁、外轭铁处的磁感应强度如图9、图10 所示。从两图中可以看出两种方法分析的结果基本一致。

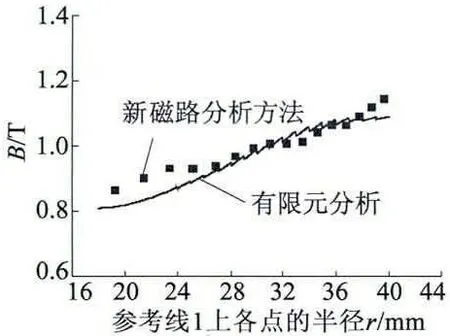
图9 考虑铁心铁心材料的B-H 曲线时内轭铁的磁感应强度

图10 考虑铁心铁心材料的B-H 曲线时外轭铁的磁感应强度

对照图7、图8 可以看出，此时内轭铁和外轭铁中靠近气隙处的磁感应强度减小，远离气隙处磁感应强度增大。靠近气隙处的铁心部分磁感应强度较大，已经进入饱和区域，从图5 中可以看出此时铁心的相对磁导率迅速下降，从而导致该层的磁阻增加，使得磁感应强度下降。远离气隙处的铁心部分磁感应强度小，还在线性部分，从图5 中可以看出此时铁心的相对磁导率有所增加，从而使得该层的磁阻减小，磁感应强度增加。

图11、图12 为铁心磁导率为常数时和考虑铁心材料的B-H 曲线时气隙处(图6 中参考线3 处)的磁感应强度。从两图中可看出气隙磁感应强度在永磁体中心部位比较接近，在永磁体的两端相差比较大，这是因为新磁路分析方法忽略端部磁场泄漏。

图11 铁心磁导率为常数时气隙处的磁感应强度

图12 考虑铁心材料的B-H 曲线时气隙处的磁感应强度

3 结 语

本文通过分析直线压缩机磁路结构的特点，对磁路进行分层分析，建立以各层磁路宽度为设计变量、总磁阻最小为目标函数的优化设计模型，再通过优化计算确定各层磁路宽度，进而分析确定磁路的的磁通分布和磁感应强度。将新磁路分析方面的计算结果与有限元计算结果进行比较，结果表明该分析方法是正确的，从而为直线压缩机磁路设计和优化提供一种新的方法。

［1］ PARK K，HONG E，LEE H K.Linear motor for linear compressor［C］//16th International Compressor Engineering Conference，West Lafayette，USA:Purdue Univ.，2002:31 -38.

［2］ CAO Y G，CHEN X，WU Y N.Theoretical and experimental investigation of two pulse tube cryocoolers driven by a single opposed linear compressor［J］.Cryogenics，2014，61:154 -157.

［3］ 李志海，刘雁，宣征南，等.压缩机用直线电机不同控制方法的特性分析［J］.压缩机技术，2013，241(5):43 -47.

［4］ 徐海峰，杨坤，满长才，等.冰箱用直线压缩机系统开发［J］.低温与超导，2014，(4):45 -47，52.

［5］ 李志海，刘雁，宣征南. 直线压缩机控制方法的研究和设计［J］.微特电机，2015，43(2):47 -49.

［6］ 李志海.动圈式直线压缩机若干关键问题研究［D］. 杭州:浙江大学，2010.

［7］ 唐任远.现代永磁电机理论与设计［M］. 北京:机械工业出版社，1997.

［8］ 陈世元.交流电机磁场的有限元分析［M］. 哈尔滨:哈尔滨工程大学出版社，1998.

［9］ 刘晓辉，李志海，郑水英.基于有限元法的动磁式直线压缩机动态特性［J］.电机与控制应用，2008，35(6):1 -4.