双定子单转子旋转型行波超声电动机转子的优化设计
2015-03-12纪跃波
纪跃波,王 涛
(集美大学,厦门361021)
0 引 言
超声电动机是一种新型电机,其原理是利用压电陶瓷的逆压电效应,通过激励电压的作用使定子产生振动,之后再通过定转子间的摩擦力,实现电能到机械能的转换,使转子产生定向的转动。与传统电机相比,它具有结构简单、低速大转矩、响应速度快、不受磁场干扰等优点。在工业控制、轿车电器、计算机、智能机器人和航空航天领域有着广泛的应用前景[1-2]。
由于超声波电动机的特殊结构和运行机理,使得超声波电动机具有不同于传统电磁型电机的优点,但也有效率低输出功率小的缺点。造成这些缺点的主要原因是定、转子在相互作用时其接触面积过小,这使得弹性体中的振动能利用率不高,限制了电机的输出能力;因而有效增大定转子接触面积对于提高超声电动机效率是非常必要的。一般来说,改变定子和转子的结构可以达到以上的目的,国内外学者针对定子的设计进行了研究,并取得了一定的成果[3-6];对于转子的设计,一般都提高它的柔性,徐志科[7]用软件ANSYS 建立定转子二维接触模型,比较了刚、柔性转子情况下接触面上的应力分布,仿真结果表明柔性转子具有更好的接触范围;蒋春容[8]提出了U 型柔性转子,通过仿真证明,电机在转速和转矩上都有明显提升,原因是采用U 型转子时接触面积更大;王光庆[9]同样提出了柔性转子的设计。
针对转子的设计,本文利用有限元分析软件ANSYS,基于本实验室研发的双定子单转子旋转型超声电动机,建立定转子二维静力学和三维动力学接触模型,得到刚、柔性转子的输出性能,通过对比得出相关结论,为双定子单转子旋转型超声电动机的设计和分析提供了理论依据。
1 双定子单转子旋转型超声电动机
双定子单转子旋转型超声电动机[10]采用结构完全相同的两个定子对称布置,并且轴向压紧转子两个端面,由压簧提供预压力,通过与中间转子相连的转轴输出机械能。其结构如图1 所示。
双定子单转子旋转型超声电动机保证两个定子的工作面均匀,这样可以克服传统旋转型行波超声电动机定、转子间存在径向接触不均匀、接触范围小等缺陷,有望提高电机的转速,输出转矩和效率,具有广阔的应用前景和积极的现实意义。
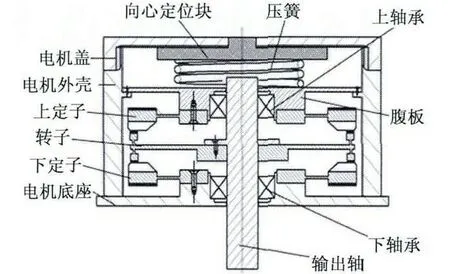
图1 双定子单转子超声电动机结构
2 定子运动方程及表面质点的运动[1]
根据Kirchhoff 薄板理论,在柱坐标系(r,θ,z)下,定子中性面的形变可用下式表示:
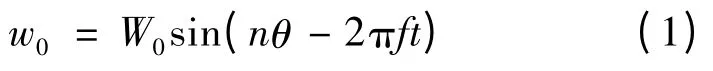
式中:W0为行波的振幅;n 为定子产生行波圆周上的波数;θ 为电机周向坐标;f 为外加电压的频率。由于定子表面的法向形变与中性层的法向形变相同,则定子表面质点的法相位移w1可表示:

若行波的相位增加180°,则有下式:
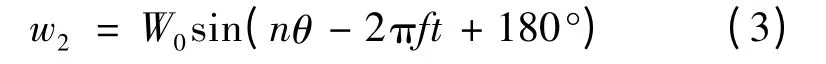
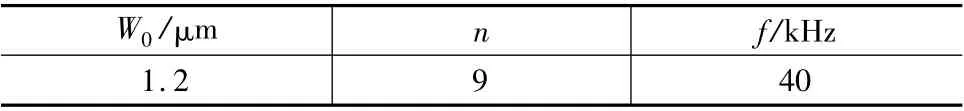
表1 位移载荷中各项参数
3 电机转子的设计
由电机结构图可以看出,本实验室研发的双定子电机的预压力是通过压簧的变形后施加在腹板上,再到上定子的支撑板上,之后再由上定子齿作用到转子上,实现定子——转子——定子之间的接触。由于预压力的施加,会使定转子间发生变形,在转子是刚性的情况下,示意图如图2 所示。

图2 预压力作用下定转子形变图
由图2 可以看到,当转子是刚性时,定转子接触面积是有限的,基本上只在转子内圈附近接触,这不仅限制了电机的输出性能,而且定转子之间磨损很严重,缩短了电机的寿命。这就需要对转子进行改进,在保证有足够的机械强度的情况下,提高转子的柔性,增加定转子的有效接触面积,使定子和转子能够平行接触。本文设计的转子结构如图3 所示,该结构中主要通过图示的柔性环节进行变形来调整转子与定子的接触配合。

图3 转子结构图
4 电机转子有限元分析
4.1 材料与结构参数的确立
本文分析的超声电动机的定子是由磷青铜组成,其尺寸如图4 所示。定子外半径Ra=30 mm,内半径ra=22.5 mm,高度ha=4.5 mm,中性层到定子上表面距离he=2.5 mm,齿高厚度ht=2 mm,支撑板长度wx,高度wy和厚度wz分别为0.5 mm,0.6 mm 和1 mm,基座内圈半径r =9 mm,高度h0=2.5 mm,螺孔到中心距离r0=13 mm,半径为2 mm。

图4 定子截面图
转子采用柔性转子,由硬铝和摩擦材料组成,两者进行黏贴,而且上下对称,其尺寸如图5 所示。外半径R1=29.5 mm,内半径R2=27.5 mm,厚度h =8 mm,h1=1 mm,h2=3 mm,b=19.85 mm;支撑板外半径R3=12 mm,内半径R4=4 mm,为了形成柔性转子,bh=0.3 mm,hh=2 mm,摩擦层厚度h3=0.3 mm。
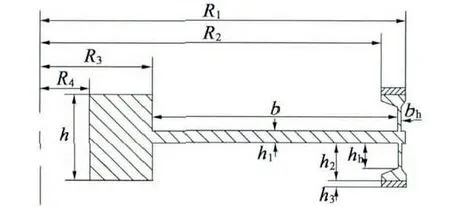
图5 转子截面图
定、转子材料参数如表2 所示。

表2 定、转子材料的主要参数
4.2 二维静力学分析
由于电机定转子结构都是轴对称的,所以对其截面分析即可,二维分析中采用PLANE42 单元,建立线线接触模型,定义摩擦系数为0.15,并消除初始渗透;根据实际情况进行约束,对下定子内圈节点进行x 和y 约束,上定子及转子的内圈节点只进行x方向的约束,在上定子支撑板节点上施加125 N 的预压力。建立的接触模型图6(a)所示。
定、转子形变情况如图6(b),在预压力的作用下,定、转子间发生了弹性变形,在上下接触面上,转子径向的变形量与定子的变形量保持一致,这样就保证了定、转子之间在径向有良好的接触,从而提高了电机的性能。
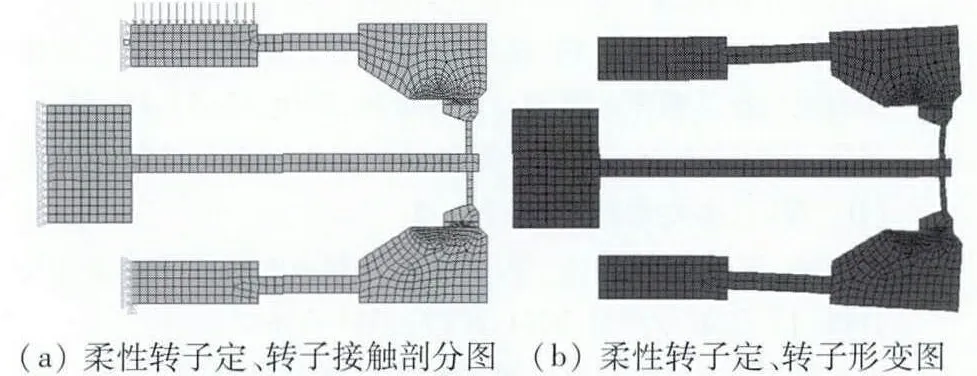
图6 柔性转子定、转子二维接触模型
接触面上的应力分布如图7 所示,由图7 可以看出,随着接触面上的位移的增加,应力由小增大,在大概26 mm 处达到最大值,上、下接触面的最大应力分别为3.91 ×105N/m2,4.78 ×105N/m2,之后逐渐减小。

图7 柔性转子上接触面与下接触面的应力分布图
为了展示柔性转子的优势,同样对刚性转子进行分析,刚性转子与设计转子具有相同的厚度及接触半径,按照前述方法建立接触模型,其应力分布曲线如图8 所示,可以看到,在预压力的作用下,随着接触面上的位移的增加,应力逐渐减小,且其中应力的最大部分主要集中在转子内圈与定子接触区域,上、下接触面的最大应力分别为1.56 ×106N/m2,1.28 ×106N/m2,这样会使应力过大且分布过于集中,导致接触面摩擦损耗大,大大缩短电机的寿命。
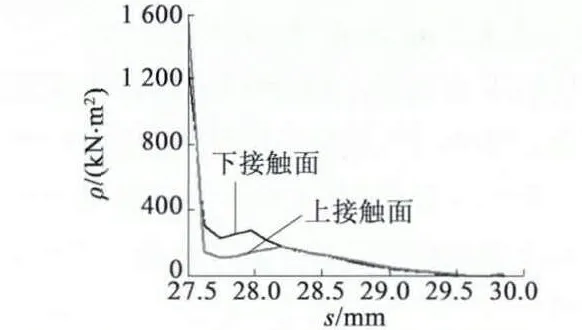
图8 刚性转子上接触面与下接触面的应力分布图
对比两种转子的应力分布曲线可以知道,柔性转子在接触面上的最大接触应力远远小于刚性转子,且应力分布相对来说较平衡,这样,既保证了定、转子间的接触面积,又减轻了摩擦层的磨损量,有利于提高电机的输出性能。
4.3 三维动力学分析
三维模型中,磷青铜、硬铝和摩擦层均采用ANSYS 单元库中的三维实体单元SOILD 95。不考虑硬铝与摩擦层粘结层的影响,为保证两者之间的重合部分力和位移传递的连续性,在划分网格前需将硬铝和摩擦层进行粘结。网格划分采用分割的方法,对计算精度贡献较大部分的网格应细化。建立面面接触模型,将定子上表面定义为目标面,与之接触的摩擦层表面定义为接触面。定义摩擦系数为0.15,并消除初始渗透。边界条件的施加应尽量反映电机实际工作情况,施加如下:(1)对下定子三个螺孔节点进行全方位约束,以阻止下定子做平移运动或周向旋转运动;(2)对上定子三个螺孔节点施加径向位移约束,以阻止上定子做平移运动;(3)对转子内圈节点施加径向位移约束,轴向保持自由,使转子不做平面平移运动;(4)分别在下定子中性面节点和上定子中性面节点施加式(2)和式(3)的位移载荷,使下定子做行波运动,而上定子做相位不断变化的行波运动;(5)在上定子支撑板表面施加轴向预压力F=125 N。柔性转子接触模型如图9 所示。

图9 有限元接触模型
求解时间为30 μs;60 个子步,以使每一子步定、转子变化量足够小;并读出每一子步结果。
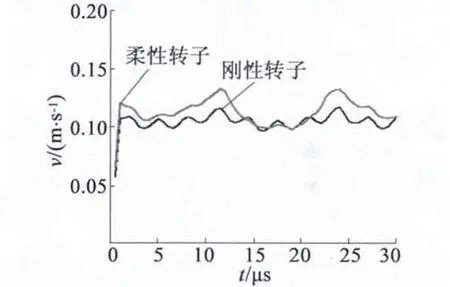
图10 刚、柔性转子质点速度对比
由图10 可以看出,在预压力为125 N 的作用下,柔性转子和刚性转子质点的速度在一定范围内波动,平均值分别为0.12 m/s 和0.11 m/s。转子的空载速度可以通过下式计算得到:
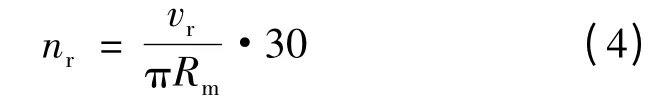
式中:vr为质点切向速度;Rm为转子半径;nr为转子转速。
图11表示的是预压力F=125N时的电机转速-转矩特性曲线。由图11 可知,当转子为刚性时,电机的空载转速为36 r/min,堵转力矩为0. 32 N·m;当转子为柔性时,电机的空载转速为39 r/min,堵转力矩为0.36 N·m。因此,采用柔性转子有利于提高电机的转矩和转速性能。
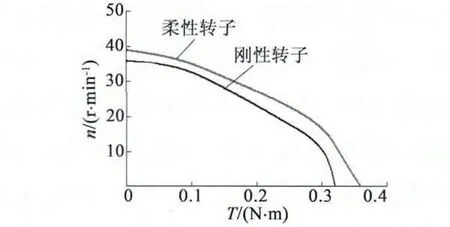
图11 刚、柔性转子电机的转矩-转速曲线比较
5 结 语
本文以双定子单转子旋转超声电动机为研究对象,针对其效率低的缺点,提出改进转子的方案,对转子进行柔性优化设计。通过建立二维静力学和三维动力学接触模型,分析了采用柔性转子时,转子接触面的压力分布及电机的转矩-转速特性;并在相同的情况下与刚性转子进行比较,得到当采用柔性转子时,电机性能及寿命均有提高的结论。仿真结果为双定子单转子旋转型超声电动机的设计和分析提供了理论依据。
[1] 赵淳生.超声电机技术与应用[M].北京:科学出版社,2007.
[2] 胡敏强,金龙,顾菊萍. 超声电机原理与设计[M]. 北京:科出版社,2005.
[3] 陈超,曾劲松,朱华,等.微型行波超声电机定子的参数优化设计[J].中国机械工程,2009,20(5):68 -72.
[4] 王一钧,胡夏夏,王志强.超声波电机定子设计参数间交互作用对电机模态频率的影响[J].微电机,2010,43(5):48 -53.
[5] 侯飞.压电定子与压电转子振型嵌合式旋转型行波超声电机[D].厦门:集美大学,2013:29 -35.
[6] 胡百振,李有光,赵淳生,等.新型纵弯超声电机振子的设计与分析[J].压电与声光,2014,36(3):353 -356.
[7] 徐志科. 行波型超声波电机的模型仿真与试验研究[D]. 南京:东南大学,2005:65 -70.
[8] 蒋春容,胡敏强,金龙,等.中空环形行波超声波电机有限元接触模型[J].东南大学学报,2014,44(1):99 -103.
[9] 王光庆.行波型超声电机的若干关键问题研究[D]. 杭州:浙江大学,2006:104 -106.
[10] 尹育聪,姚志远,赵淳生.行波型旋转超声电机两种组合方式的实验研究[J].中国机械工程,2011,22(1):84 -87.
