极槽接近表贴式永磁同步电机齿磁密解析计算

周 羽，李槐树，周 石，曹 晴

(海军工程大学，武汉430033)

0 引 言

与传统电机相比，永磁同步电机具有高功质比、高转矩体积比、高效率和振动噪声小等优点，它已经广泛用于商业、工业和军工等产品［1-3］。永磁同步电机气隙磁场的准确计算是电机各种性能分析的基础，例如:绕组电感［4］、反电动势［5］、损耗［6］、径向力［7-8］、齿槽力矩［9］、不平衡力［10］、振动与噪声［11］等。目前，在不简化电机结构并考虑磁性材料饱和的前提下，磁场计算的有限元数值方法能得到提供精确的永磁电机磁场计算结果。但是这种数值方法非常费时，不利于电机优化设计，一般只用于验证电机解析优化设计的最终结果。而且网格剖分对有限元数值计算的结果影响有时较大，特别是在计算齿槽力和不平衡电磁力时［12-13］。事实上，通过合理的假设，磁场解析计算方法能够更快速灵活准确地计算并分析电机的各种性能［14］。

极槽接近永磁同步电机是一种特殊结构，具有低速大转矩和超高功率密度的优点。由于结构的特殊性，在考虑定子铁心磁性材料饱和的前提下，计算反电动势、电感等参数必须以单个齿部的磁密为基础。但是目前极槽接近永磁同步电机定子齿磁密的相关研究比较少。

本文利用面电流等效法，在不开槽时推导了气隙磁密的解析计算公式，在此基础上，提出了截取加三次函数拟合法计算考虑饱和时的电机定子齿部最大磁密。用有限元法对定子齿部最大磁密进行了计算，验证了截取加三次函数拟合法具有较高的精度。最后根据时步有限元法，得到极槽接近永磁同步电机的齿部磁密具有正弦周期性。

1 无槽磁场计算

1.1 一对线圈产生的磁场

电机中二维空间平面场域上的电磁场可以在极坐标系中进行分析计算，且其矢量磁位满足泊松方程［15］:

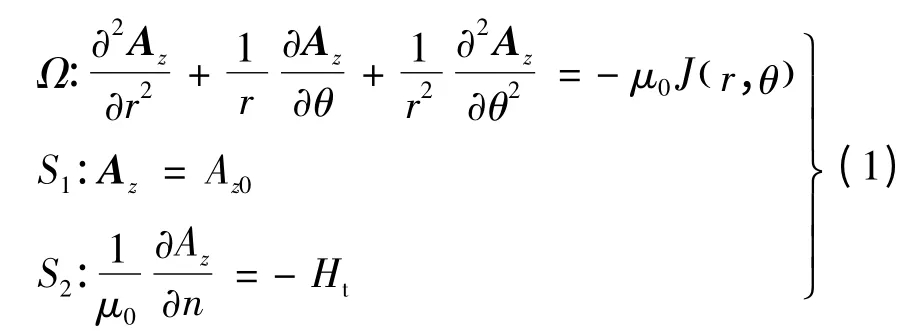
式中:μ0为磁导率，且μ0=1/ν，ν 为磁阻率;Ht为磁场强度的切向分量;Az为z 轴方向的矢量磁位;J(x，y)为源电流密度;S1为第一类边界条件;S2为第二类边界条件。

假设定、转子铁心的导磁率μFe=∞，如图1 所示，导线A 和B 的位置为r =b，θ = ±α 处。一对通电线圈由两根通电导线组成，把每根带电流导线产生的矢量磁位叠加，可得到一对通电线圈在气隙中产生的矢量磁位［16］。

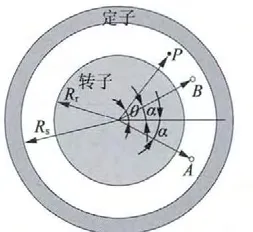
图1 气隙中一对载流线圈

电机定子和转子之间气隙的磁场边界条件:

(1)电机转子外表面，磁通密度切向分量为零，即:r=Rr时，Bθ=0

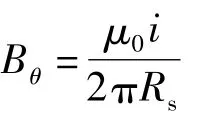
定子和转子之间的气隙属于通电线圈以外的区域，在这些区域内的电流密度J(r，θ)=0。根据边界条件(1)和边界条件(2)以及分离变量法求解泊松方程，得到一对通电线圈在气隙中P 点产生的矢量磁位:

于是一对通电线圈在半径为Rs位置的径向气隙磁密(本文后面求得的磁密均为半径为Rs位置处的径向磁密:

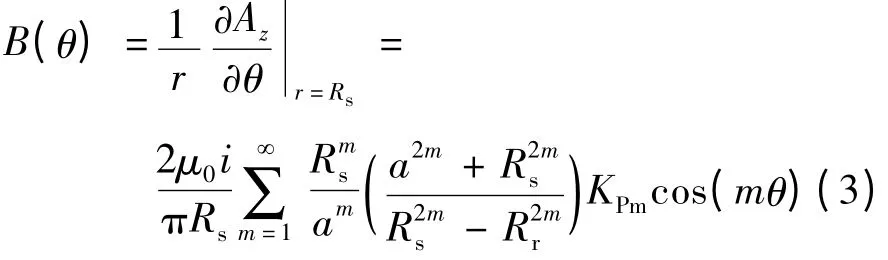
式中:KPm=sin(mα)为m 次谐波的节距因数。

1.2 平行充磁永磁体产生的气隙磁密

在表面式永磁电机中，瓦片形磁极有平行充磁和径向充磁二种。其中，同圆心不同半径瓦片形磁极的永磁电机结构如图2 所示，其中p 为永磁电机极对数，hm为永磁体厚度，2η 为永磁体的张角，Rr为电机转子外半径，Rs为电机定子内半径。

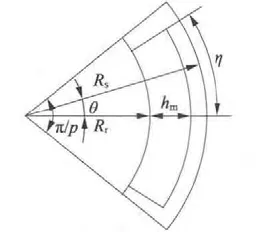
图2 瓦片形永磁体尺寸

由于充磁工艺的限制，标准径向充磁的瓦片形永磁体很难得到，而平行充磁的瓦片形永磁体的充磁工艺简单且容易得到，分析并计算平行充磁瓦片形永磁体在电机气隙中产生的磁场更有实用价值。

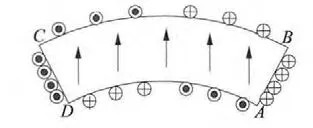
图3 平行充磁时的面电流

平行充磁的瓦片形永磁体的磁化方向和各边等效面电流方向如图3 所示。根据永磁体的面电流等效法，图中永磁体AB 和CD 的等效面电流大小相等且方向相反，其电流密度的大小可以表示:

式中:Hcb为永磁体矫顽力。

沿BC 和AD 边变化的面电流密度的大小:

一个平行充磁同心瓦片形永磁体AB 和CD 段的等效面电流在电机气隙中产生的磁密:

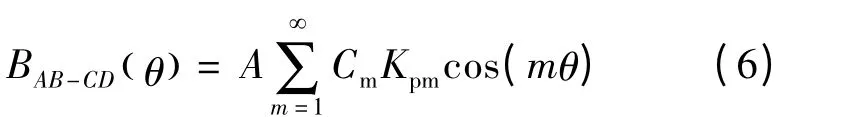
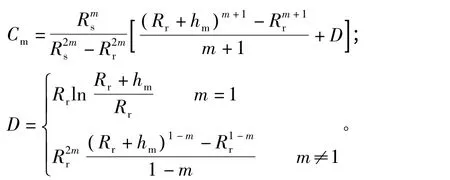
BC 段面电流产生的磁密:

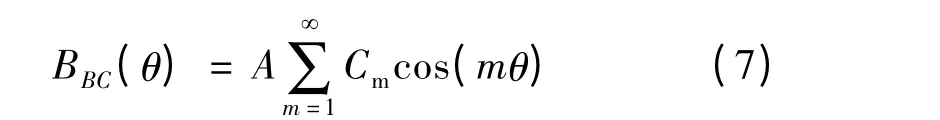
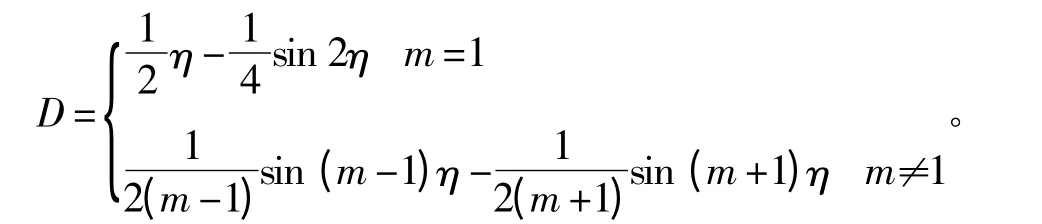
在Cm中，b=Rr+hm。

AD 段面电流产生的磁密:

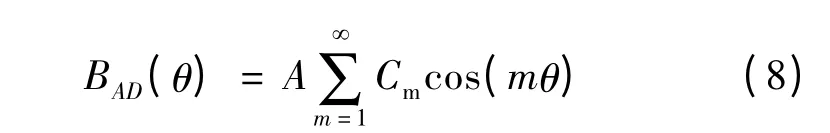
一个平行充磁的永磁体在定子内表面产生的磁密B1( )θ 为AB，CD，BC 和AD 各段的叠加，即:

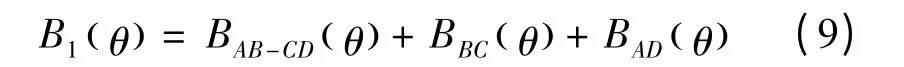
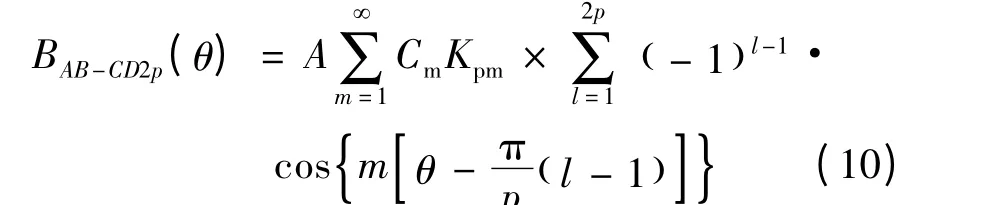
式中:A，Cm，Kpm和式(6)相同。

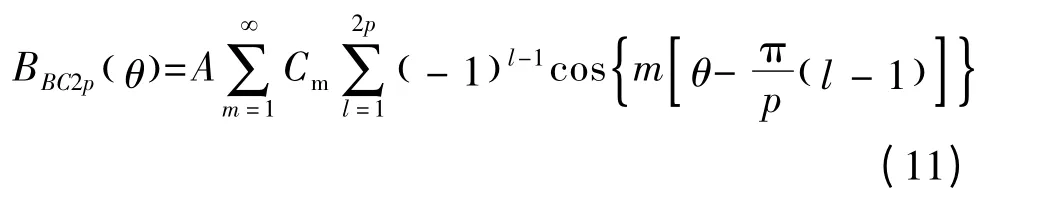
式中:A，Cm和式(7)相同。

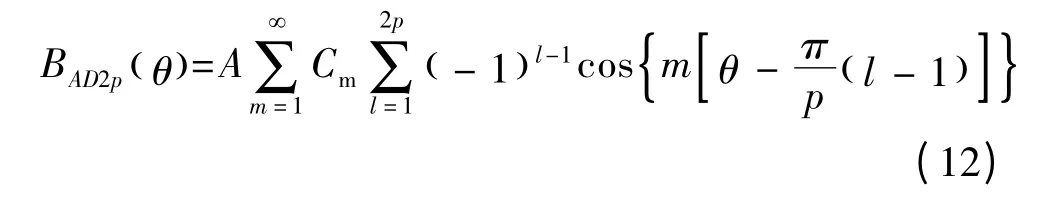
式中:A，Cm和式(8)相同。

于是多极平行充磁同心瓦片形永磁体在永磁电机的定子内表面产生的磁密:

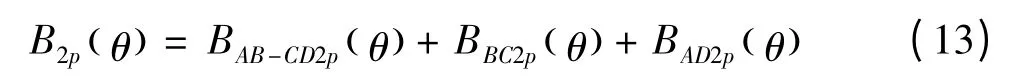
上述公式都是在定子和转子表面光滑时推导得到的。

2 齿部最大磁密计算

极槽接近永磁同步电机结构特殊，一个永磁极的磁力线基本通过一个齿达到另一个磁极，并构成闭合磁路。为了充分利用磁路结构，使电机磁路和电路的利用率达到最大，提高永磁电机的功率密度，设计极槽接近永磁同步电机时，齿部磁密通常会达到较大的饱和。绝大多数文献对电机磁场计算时都假设定子和转子铁心的导磁率为无穷大，忽略电机定子齿部的磁密饱和等非线性因素的影响。在这种假设前提下，当齿中心线和极中心线正对时，由磁极进入齿面的磁力线将全部通过定子齿部和定子轭部，但是定子齿部铁心在饱和影响下，电机槽口和槽肩的漏磁将会比较大，这是不容忽视的。非极槽接近永磁同步电机一般以定子内表面的磁通为有效磁通计算反电动势，而在计算极槽接近的永磁同步电机的反电动势时，有效磁通是每个齿的磁通。

如图4 所示，N 极中心线和齿中心线正对时，齿部的磁密最大，极槽接近永磁同步电机的极面宽度和齿面宽度不相等且相差较小，图中tm为齿面的宽度。计算进入齿面的有效磁通时，本文采用磁通截取法:根据式(13)计算得到定子无槽时电机定子内表面的径向磁密如图5 所示;在图4 中，截取N 极与齿面正对的磁通作为开槽时由气隙进入齿面的磁通，此磁通即为计算齿部磁密的截取磁通φjq。由于槽口影响，没有被截取的磁通将作为气隙漏磁直接和邻近的永磁体构成气隙漏磁路。

表1 是两种极槽接近的永磁同步电机的基本尺寸，表2 是以表1 的电机结构为基础，改变极对数p、槽数Ns、永磁体厚度hm、气隙厚度δ 和齿宽ts时，8 个样机的齿部最大磁密、截取磁通以及相对磁导率的对比表。表2 中，齿部最大磁密为有限元计算结果，其余均为解析计算结果。本文中，考虑饱和的硅钢片选为50DW350。

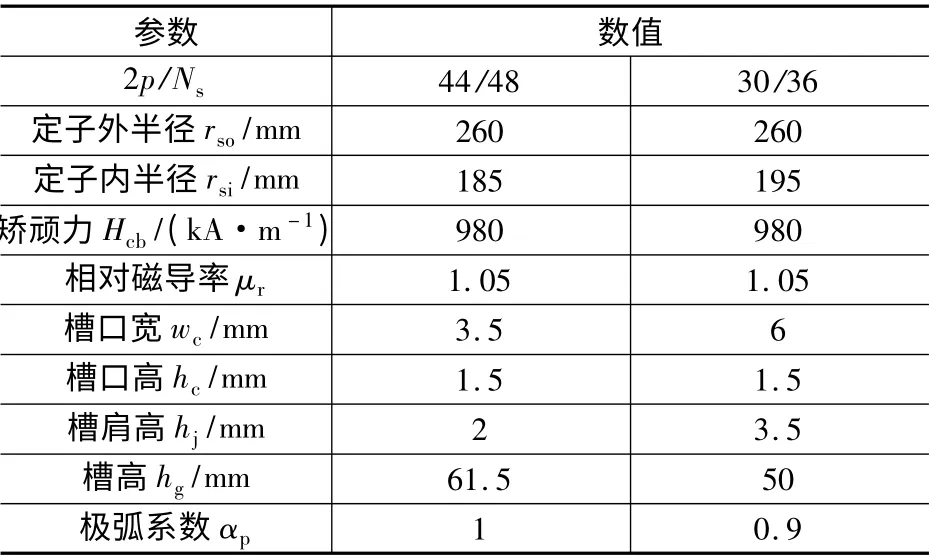
表1 样机参数

根据齿部磁密的有限元结果，查表得到表2 中齿部的磁感应强度H，并计算得到齿部的相对磁导率μr。由表2 中的相对磁导率计算结果可以看出，极槽接近的永磁同步电机中铁心的磁导率不能假设为线性或是无穷大，必须考虑饱和影响。

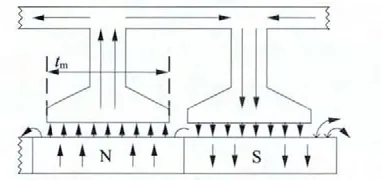
图4 电机主磁路

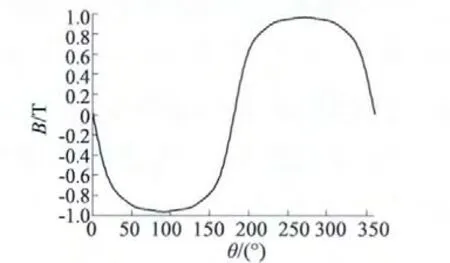
图5 不开槽时定子内表面径向磁密

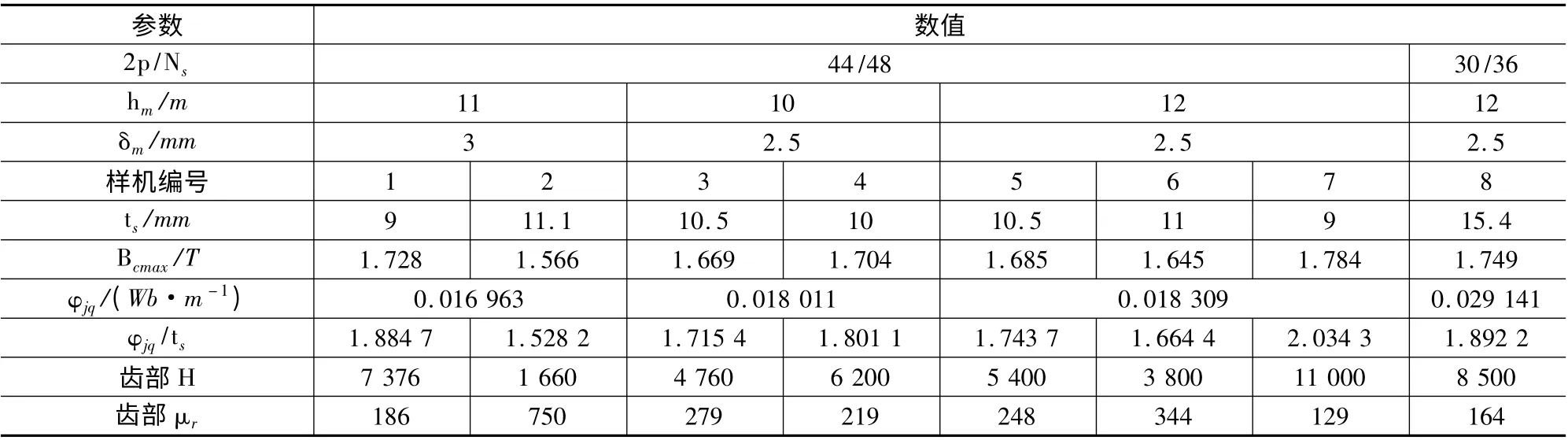
表2 最大齿磁密计算结果

齿部磁通计算公式:

Bcmax为齿部最大磁密，ts为齿宽，leff为电机轴向长度，本文中设定为单位长度，不影响计算结果。

齿宽、齿部磁通和齿部磁密存在式(14)的关系，由于受到磁路饱和等非线性因素的影响，齿部磁通很难得到，因此本文以齿宽和齿面磁通作为变量，采用有限元和解析计算相结合的方法寻找规律，得到计算极槽接近永磁电机的齿部最大磁密公式。

定性分析可知，ts增大Bcmax减小，φjq增大Bcmax增大，可以方便地把ts和φjq两个变量简化为φjq/ts一个变量，采用截取法加三次函数拟合的方法。取表2 中样机编号为2，4，6，7 的φjq/ts结果进行三次函数拟合，得:

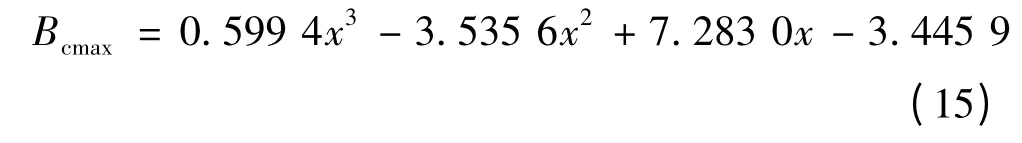
3 有限元验证

表2 中1，3，5，8 号样机用于验证拟合方法的正确性，这种方法是针对定子铁心材料B -H 曲线非线性部分的局部拟合法。在设计高功率密度的极槽接近永磁同步电机时，齿部磁密的最大值通常在本文拟合范围之内。表3 以有限元结果为基准，列出了截取法和截取加拟合法的误差结果，易知在考虑饱和情况下，截取加三次函数拟合法较高的精度，非常适用于电机工程设计。

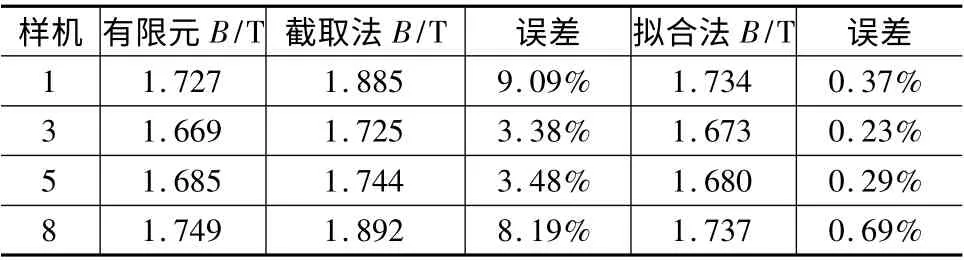
表3 齿部最大磁密误差比较

截取法和截取加三次函数拟合法的齿部最大磁密对比结果如图6 所示。当拟合函数曲线的横坐标小于交点处的横坐标时，由于定子齿面边端的聚磁效应占主导，槽漏磁较小，进入齿面的磁通大于截取法得到的磁通，拟合法得到的齿部磁密大于截取法得到的齿部磁密;当拟合函数曲线上横坐标大于交点处的横坐标时，槽漏磁占主导，聚磁效应相对较小，随着实际齿部磁密的增大，槽漏磁增大，拟合法得到的齿部磁密小于截取法得到的齿部磁密。

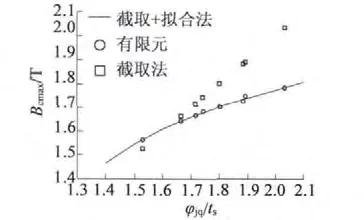
图6 三种方法计算结果

对平行充磁同心瓦片型永磁同步电机，对表2中5 号和8 号极槽接近的永磁同步电机进行Ansys建模，利用时步有限元法计算得到一个电角度周期内的齿部磁密波形如图7 和图8 所示。电机定子齿宽相等，齿部磁密保持均匀分布。由图7(b)和8(b)可知，齿部磁密的谐波较小，实际波形接近正弦，定子开槽设计使定子磁路饱和并产生较大的槽漏磁。因此，用解析法计算齿部磁密时，只需要计算齿部磁密的最大值，然后根据齿部磁密的正弦周期性得到不同位置时的齿部磁密。

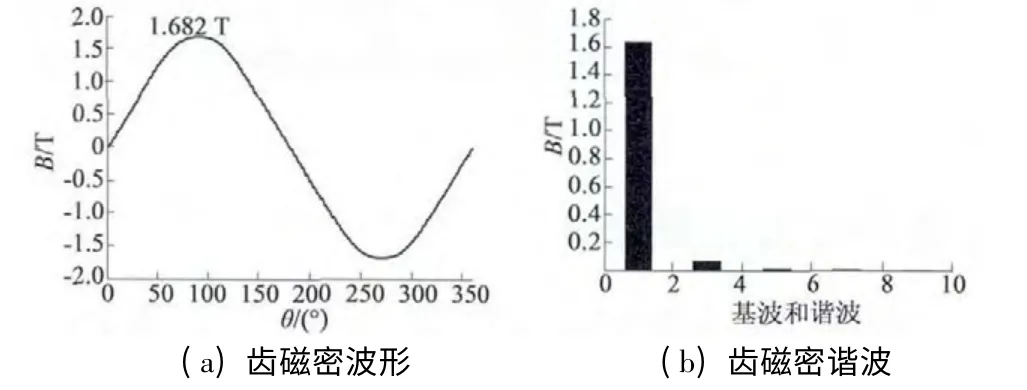
图7 5 号电机一个电周期内的齿磁密

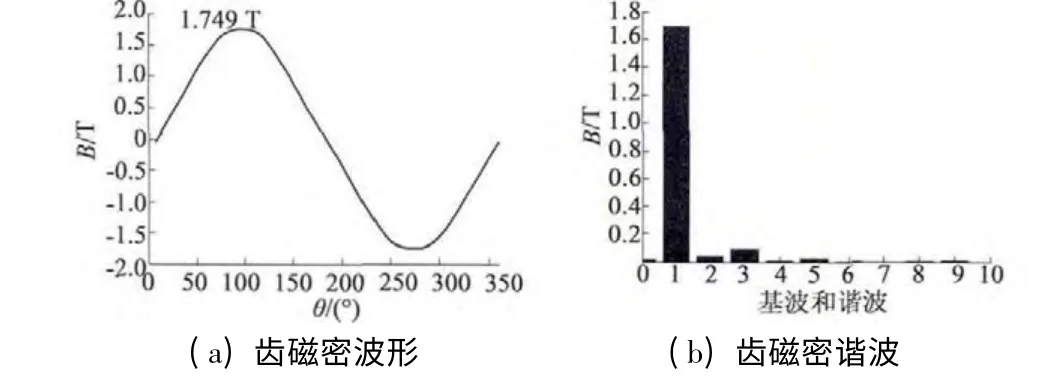
图8 8 号电机一个电周期内的齿磁密

4 结 语

本文利用面电流等效法，在不开槽时推导了气隙磁密的解析计算公式，提出了截取加三次函数拟合法计算考虑饱和时的电机定子齿部最大磁密。用有限元法验证了截取加三次函数拟合法，定子齿部最大磁密的解析计算结果误差在1%以内。最后根据时步有限元法证实，极槽接近永磁同步电机的齿部磁密具有正弦的周期性。在考虑定子铁心饱和的前提下，本文所提的方法非常适合极槽接近的永磁电机齿磁密计算，对此类型永磁电机的设计和性能分析有很大的帮助。

［1］ ZHU Z Q，HOWE D. Electrical machines and drives for electric，hybrid，and fuel cell vehicles［J］.Proc. of IEEE，2007，95(4):746 -765.

［2］ ZHU Z Q，CHAN C C.Electrical machine topologies and technologies for electric，hybrid，and fuel cell vehicles［C］//IEEE Vehicle Power and Propulsion Conference，2008:1 -6.

［3］ EI-REFAIE A M. Fractional -slot concentrated -windings synchronous permanent magnet machines:Opportunities and challenges［J］. IEEE Trans. on Ind. Electron.，2010，57(1):107 -121.

［4］ ZHU Z Q，HOWE D，BIRCH T S. Calculation of winding inductances of brushless motors with surface mounted permanents magnets［C］//CEM，Paris，France，1994:5 -8.

［5］ MILLER T J E，RABINOVICI R.Back-EMF waveforms and core losses in brushless dc motors［J］.Proc. Inst. Elect. Eng.，1994，141(3):144 -154.

［6］ DENG F. An improved iron loss estimation for permanent magnet brushless machines［J］. IEEE Trans. on Energy Convers.，1999，14(4):1391 -1395.

［7］ WANG J，XIA Z P，LONG S A，et al.Radial force density and vibration characteristics of modular permanent magnet brushless ac machine［J］.IEE Proc. of Electric Power Appl.，2006，153(6):793 -801.

［8］ ZHU Z Q，XIA Z P，WU L J，et al.Analytical modelling and finite element computation of radial vibration force in fractional - slot permanent magnet brushless machines［J］. IEEE Trans. on Ind.Appl.，2010，46(5):1908 -1918.

［9］ MARKOVIC M，JUFER M，PERRIARD Y. Reducing the cogging torque in brushless DC motors by using conformal mappings［J］.IEEE Trans. on Magn.，2004，29(2):451 -455.

［10］ ZHU Z Q，ISHAK D，HOWE D，et al.Unbalanced magnetic forces in permanent - magnet brushless machines with diametrically asymmetric phase windings［J］. IEEE Trans. on Ind. Appl.，2007，43(6):1544 -1553.

［11］ 杨浩东，陈阳生.分数槽永磁同步电机电磁振动的分析与抑制［J］.中国电机工程学报，2011，34(24):83 -89.

［12］ LIN D，HO S L，FU W N.Analytical Prediction of Cogging Torque in Surface - Mounted Permanent - Magnet Motors［J］. IEEE Trans. on Magn.，2009，45(9):3296 -3302.

［13］ WANG D H，WANG X H，QIAO A W，et al. Reducing Cogging Torque in Surface-Mounted Permanent-Magnet Motors by Nonuniformly Distributed Teeth Method［J］.IEEE Trans. on Magn.，2011，47(9):2231 -2239.

［14］ DUBAS F，ESPANET C.Analytical solution of the magnetic field in permanent-magnet motors taking into account slotting effect:No-load vector potential and flux density calculation［J］. IEEE Trans. on Magn.，2009，45(5):2097 -2109.

［15］ 唐任远.现代永磁电机理论与设计［M］.北京:机械工业出版社，1997:63 -64.

［16］ 潘元璋，让余奇，黄克峰.表面贴磁式永磁同步电动机空载气隙磁场解析计算［J］.防爆电机，2012，47(6):1 -5.