轴向永磁涡流联轴器导体盘的结构分析

李 申，李延民，苏宇锋

(郑州大学，郑州450001)

0 引 言

永磁涡流联轴器自1999 年问世，初始在泵、风机等设备上运用，很快受到众多企业的认可，十多年间得到快速的发展。永磁涡流联轴器通过磁场传递转矩，没有任何机械连接，使得在传递转矩和运动的同时，隔离振动、承受冲击载荷、实现过载保护。由于主动端与从动端存有气隙，安装的对中性要求不严格，相应地降低设备的安装成本。永磁涡流联轴器的功能优于传统的机械式联轴器。起动频繁的机械，可作为液力耦合器的替代品，实现调速和节能。

国内外有很多文章对永磁涡流联轴器进行了分析研究，提出各种设计方法。其中文献［1］提出铜盘的结构，对铜盘厚度进行了分析;文献［2］提出了一种鼠笼式的导体盘结构;文献［3］提出一种开槽式的导体盘结构，并对开槽的数量进行了研究。大多文献从一种永磁体盘的结构参数进行研究，以获得铜盘区域最大磁场强度，缺少对导体盘的各种结构分析比较。

本文使用磁阻法推导出导体盘区域的磁场强度，利用楞次定律推导传递转矩。通过对三种导体盘结构(环状导体盘、条状导体、开槽导体盘)进行参数分析，通过比较来说明导体盘结构参数的影响，得出一种性能较优的结构和相应的参数。

1 转矩计算的基本原理

永磁涡流联轴器由两大部分构成，其基本结构如图1 所示。永磁盘转子和导体盘转子，两者之间存在气隙。其中导体盘转子与电机轴相连，为主动端;永磁盘转子与负载相连，为从动端。导体盘切割永磁体产生的磁场，产生涡电流形成感应磁场，两磁场相互作用传递运动和转矩。通过调节气隙的大小，可以改变输出轴转速，实现速度的调节。

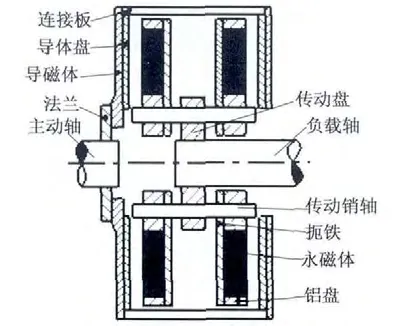
图1 永磁涡流联轴器的基本结构

通过磁阻法进行永磁涡流联轴器传递转矩的计算，计算出导体盘区域磁感应B，再通过法拉第电磁感应定律，得到在一定转速差下所产生的感应电动势，计算涡电流等效电流的大小，和所产生的安培力(楞次定律)，进而求出传递转矩。

永磁涡流联轴器的简化模型和等效磁路如图2所示，其中导磁体的磁阻较小，可忽略不计。

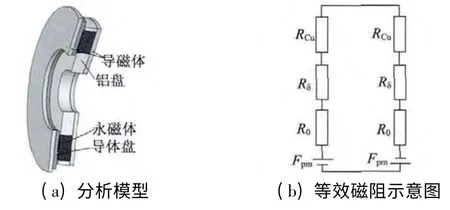
图2 分析模型与等效磁路

每块永磁体所产生的等效磁动势Fpm:

式中:Hc为永磁体材料的矫顽力;hpm为永磁体厚度。

根据磁阻计算公式［4］，假设磁路通过各个区域的面积相等，可得到各个部分的磁阻大小:

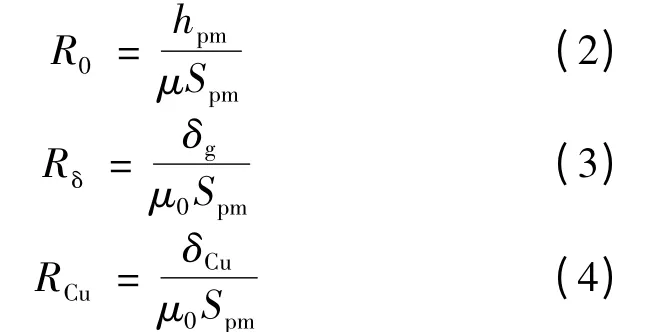
式中:R0为永磁体磁阻;μ 为永磁磁体相对磁导率;Spm为永磁体截面积;Rδ为气隙磁阻;δg为气隙厚度;μ0为空气磁导率;δCu为铜盘厚度;RCu为铜盘区域的磁阻。

通过气隙和导体盘区域的磁通量Φ、铜盘区域的磁感应强度B 按下计算:

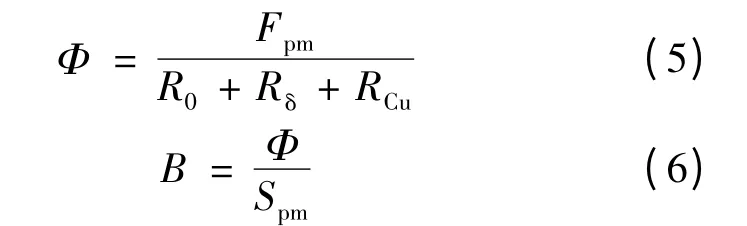
得到B 后，根据法拉第电磁感应定律可得出一块永磁体在导体盘区域所产生的电动势E:

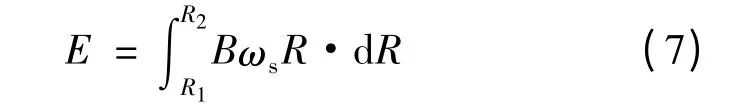
式中:R1，R2为永磁体的内、外半径;ωs为导体盘与永磁体盘的相对转速。

由永磁体在铜盘上所产生的感应电动势E，根据电流的路径，算出相应路径的电阻R:

式中:ρ 为铜的电阻率;Lp为一个等效电流所经过的路程;S 为横截面积。

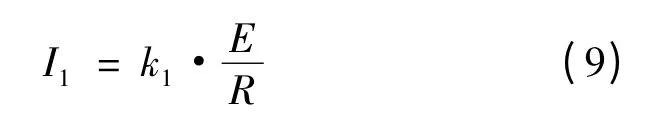
因电流的形式为涡流，相邻反向的涡流使得电流相对排列规则，算出的电阻和电流的大小通过系数k0，k1进行修正。又因在永磁体对应的铜盘区域不仅有自身的电流I1通过，还有相邻电流的通过，所以表现电流I 的大小为自身的两倍:

电流路径上每小段dl 所受的安培力［5］:

一块磁铁产生的转矩为T1，n 块磁体产生的总转矩T:

导磁体在磁场中所受的吸引力可根据Maxwell公式计算［6］:

本文主要对导体盘的结构参数进行分析，采用的永磁体参数:12 对永磁体，厚18 mm，形状为扇形，内外半径分别为63 mm 和99 mm，占空比为75%。传动功率7.5 kW，转速1500 r/min。由于联轴器的结构为对称形式，仅对一侧进行分析，传动转矩23.75 N·m。

2 导体盘参数分析

轴向永磁涡流联轴器中的导体盘参数是影响传递转矩两大参数之一，另一个是永磁体参数。本文通过导体盘中涡流的形成与路径特点，总结并分析了三种导体盘结构对传递转矩与轴向力的影响，环状导体、条状导体以及开槽导体，其结构如图3 所示。

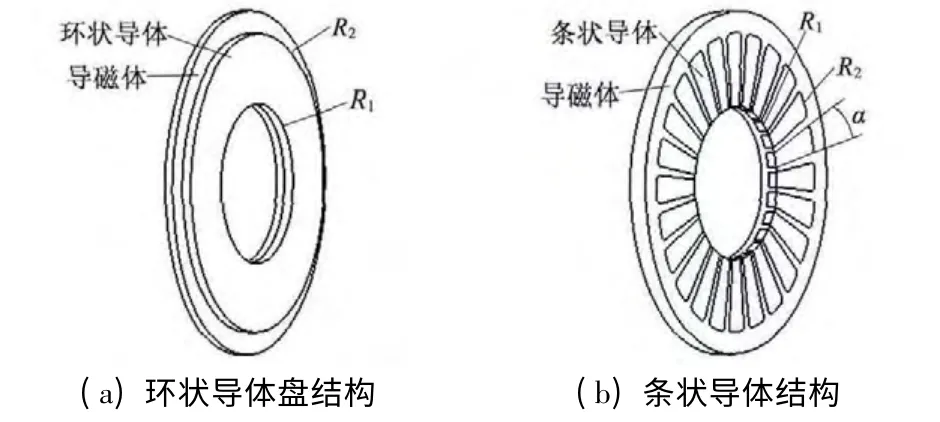
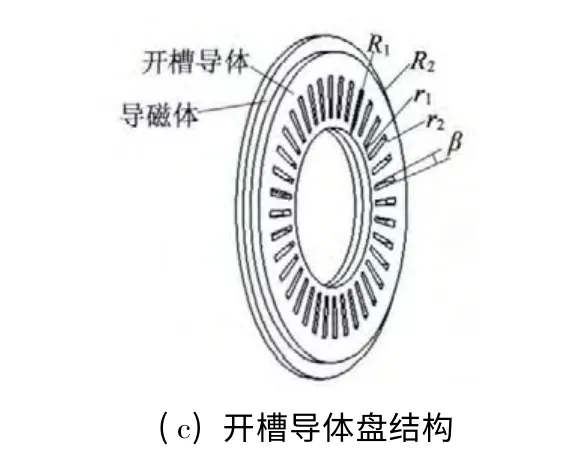
图3 不同形式的导体盘

2.1 环状铜盘

由于铜的导电系数较大，导体盘的材料选为铜，本文所说的导体盘即为铜盘。环状铜盘内外径为R1，R2，铜盘厚度为δc，结构如图3(a)所示。永磁体与导磁体的距离是决定静止时吸引力的关键因素，当这个距离较大时，吸引力较小，并且通过气隙的漏磁增加，传递的转矩降低;距离较小时则相反。选择合适的铜盘厚度:在较小的吸引力下，有较高的传递转矩。

导体盘切割永磁体产生的磁场，产生涡电流的过程存在集肤效应，导体盘中感应电流的集肤深度δ:

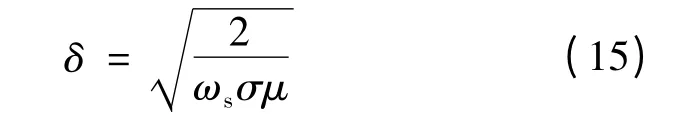
式中:σ 为材料电导率;μ 为材料的磁导率。

设计选取的ωs=50 r/min，得到δ =17.4 mm，渗透厚度较大。这里为了得到铜盘区域较强的磁感应强度，选取厚度小于17 mm 的导体盘。铜盘厚度小于正常工作下的集肤深度，可以忽略集肤效应的影响。

图4 不同铜盘厚度下的转矩和轴向力

通过Ansoft Maxwell 仿真可以看出，铜盘厚度对转矩和轴向力的影响。从图4 中可以看出，当铜盘的厚度增加时，轴向力在减小，铜盘厚度在4 ～8 mm时转矩为最大的范围。这里为了使得轴向力较小，传递转矩较大，取铜盘厚度为7 mm，永磁体到导体盘的气隙为2 mm。

导体盘外径对转矩有影响，如图5 所示。

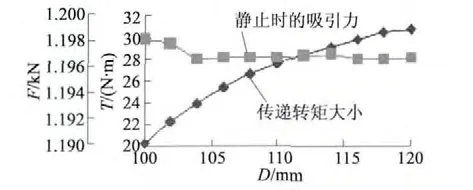
图5 不同铜盘外径下的转矩和轴向力

从图5 可以看出，在一定范围内随着导体盘外径增大，传递的转矩增大。其中的原因可根据仿真结果中涡流的矢量图(图6)得知:外径较大时，为涡电流最外端提供的路径较大，整体形成的反感磁场强度较大，达到增加转矩的效果;还有当半径增大，相当于整个涡流耦合的回转半径增大，所以传递的转矩增加。

2.2 条状导体

条状导体是多个梯形的导体镶嵌在导磁体上，构成导体盘结构，如图3(b)所示。

理论上，导体盘切割磁力线形成安培力，安培力在半径上的积分得出转矩。导体盘中所形成的涡电流，各个方向都有，但其中作用较大的是沿半径方向的电流，假定去除部分材料，可以只保留半径方向上的电流，这是使用条状导体的前提条件。通过条状导体切割磁感线，形成半径方向上电流，电流所受到的安培力形成能够传递转矩。

选取的铜条的圆心角分别为α =22. 5°，α =16.8°，α=11.2°。每一圆心角选取不同的筒体数量，建立模型进行仿真分析。

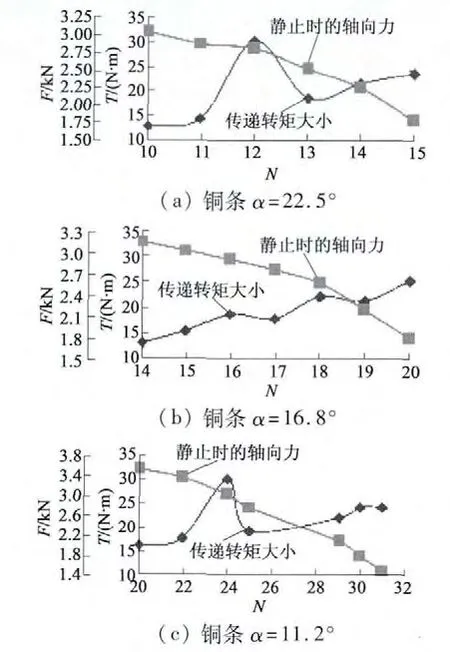
图7 铜条在不同圆心角、不同数量时的转矩和轴向力

图7 显示的转矩大小小于铜盘的额定转矩。并且当数量为永磁体数量的倍数时，仿真结果值跳动非常大。初始的假设不成立，这是由于两盘是相互旋转的，存在转速差。当导体盘中有较多条状导体时，所形成的转矩较大，而当与永磁体所对应区域缺少条状导体时，所形成的转矩较小。并且条状结构所形成的电流缺少回流的路径，这也是形成转矩相对较小的原因。所以对于永磁体涡流联轴器条状结构并不适用。

2.3 开槽的导体盘

通过上述分析，条状导体并不适用，根据文献［3］，环状导体通过开槽可以减少非半径方向上电流的存在，从而提高感应电流的利用，并能节省材料，提高联轴器的性能，这种结构类似鼠笼式结构［2］。根据涡电流的形状，在导体盘上开一些矩形的空槽，来增加半径方向上电流的强度，其结构如图3(c)所示。

开槽圆心角分别为β =1°，β =2°，β =3°，β =4°，槽的内、外径分别为65 mm 和95 mm，通过建立模型，得到的仿真结果如图8 所示。

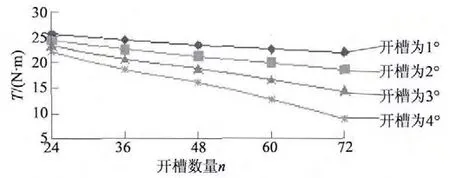
图8 不同开槽角度和不同数量时铜盘的转矩

开槽铜盘所得到的传递转矩小于整块铜盘，大于条状导体所得的转矩。由于转速差的存在，当永磁体所对应的区域，存在导体时，转矩较大;而不存在导体时，转矩骤减，这是转矩小于整块铜盘的原因。通过观察涡流的形成，开槽的铜盘为涡流提供了回流的路径，条状结构缺少回流路径，所以开槽的铜盘所形成的转矩相比于条状结构较大。开槽铜盘随着模型参数的变化，静止时的吸引力不变，为1.196 N，说明静止时的轴向力只和永磁体与导磁体之间的距离有关。

通过上述三种结构的比较可以得知:铜盘切割磁感线所形成涡电流，是瞬时变化的，涡流一直在铜盘上永磁体区域所对应的位置。对减小轴向力，提高转矩效果较好。

3 开槽铜盘填充导磁体

根据磁学原理可知，当有相同大小的励磁电流，采用磁导率较高的铁心材料，所产生的磁通较大。运用到本文中，可通过导磁体填充开槽的导体盘来增大反感磁场，其结构如图9 所示。

图9 开槽导体盘填充导磁体结构

通过改变开槽大小和开槽数量，建立模型进行仿真分析。从图10 中看出，转矩较大，超过了环形铜盘所形成的转矩，轴向力较大。其原因有两种可能:①由于导磁体与永磁体距离较近，减小气隙，增加了铜盘区域的磁感应强度，甚至抵消了开槽所产生的影响，故增加了转矩。②对于同样大小的涡电流，加铁心与不加铁心的区别。填充铁心时，涡电流会有较大的磁感应强度产生;没有填充铁心时，涡电流产生的磁感应强度较小。综上原因，开槽填充铁的结构，有较大的传递转矩，缺点是存在较大的轴向力，结构上较为复杂，制造难度大。

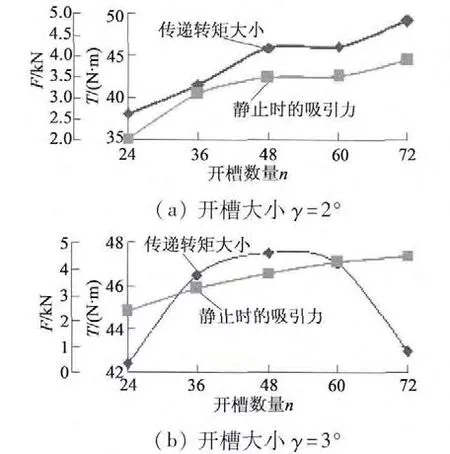
图10 不同开槽大小填充导磁体后的转矩与轴向力

4 结 语

(1)导体盘厚度在4 ～8 mm 时对转矩的影响不大，对轴向力的影响较大。导体盘外径对传递的转矩有影响。

(2)条状导体由于转速差的存在，并缺少回流路径，能够传递的转矩小于环状的铜盘结构和开槽导体盘的。

(3)开槽后的导体盘因为转速差的存在，虽然减少了非半径方向上电流，但对联轴器的传递转矩没有提高。

(4)开槽后的导体盘，通过填充导磁体，对转矩有较大的提高，但存在增大轴向力的缺点。

综上所述，对于利用转速差形成反感磁场的永磁涡流联轴器，环状结构铜盘对减小轴向力，提高转矩效果比较好。

［1］ 李桃，林鹤云，黄允凯.基于三维运动涡流场分析的永磁涡流联轴器特性［J］.东南大学学报(自然科学版)，2010，40(2):301 -305.

［2］ 陈志鹏，杨超君，孔令营.鼠笼异步磁力联轴器隔离套的损耗计算及温度场分析［J］.机械传动，2014，(4):114 -118.

［3］ RAZAVI K H，LAMPERTH U M. Eddy - current coupling with slotted conductor disk［J］.IEE Transactions on Magnetic，2006，42(3):405 -410.

［4］ 万援.调速型稀土永磁磁力耦合器的性能研究［D］. 沈阳:沈阳工业大学.2013:9 -15.

［5］ GAO Qingzhong，WANG Daizhi，LIN Sheng. The eddy-current analysis and transmit-torque calculation for the permanent eddycurrent coupling based on the equivalent - depth method［C］//International Conference on Mechatronics and Automation，2014，8:1318 -1322.

［6］ LUBIN T，REZZOUG A. Steady -state and transient performance of axial - field eddy - current coupling［J］. IEE Transactions on Industrial Electronics，2014，62(4):2287 -2296.