某型舰船用转子系统动力学性能分析

王 嵩，张胜文，彭世警，李国平，章 艺，周 璞

(1．江苏科技大学机械工程学院，江苏镇江212003;2．中国船舶重工集团公司第七○四研究所，上海200031)

0 引言

转子系统作为发动机、汽轮机等旋转机械的核心部件，其广泛应用于航空航天、船舶、汽车、农机、军事等领域。随着国家现代化和军事现代化的发展，对舰船转子系统的可靠性、安全性、隐身性等性能提出了更高要求，而其动力学的研究是现在关心的重点。转子动力学的主要研究内容包括转子的临界转速及振型分析、不平衡响应分析和稳定性分析，而其分析又必须以轴承动特性为前提［1］。

传统分析方法中，未对轴承的弹性支撑特性和转子系统的陀螺效应进行充分考虑，使得分析结果有偏差。本文则以某型转子系统为研究对象，研究其支撑轴承的动特性，求出其刚度和阻尼［2］;利用Ansys建立转子系统有限元模型，对其进行临界转速分析、不平衡响应分析、匀加速响应分析和冲击响应分析，在设计阶段预测和分析其动力学性能，避免共振和响应过大问题，提高设计效率和产品安全可靠性［3－8］。

1 轴承动特性分析

轴承作为连接件，其刚度直接影响到整个机构的动态特性。轴承包括两大类即滑动轴承和滚动轴承，由于结构和作用机理不同，其研究方法也不同。

1.1 滑动轴承动特性

对滑动轴承的研究，主要计算参数包括支撑刚度和阻尼。滑动轴承无量纲雷诺方程:

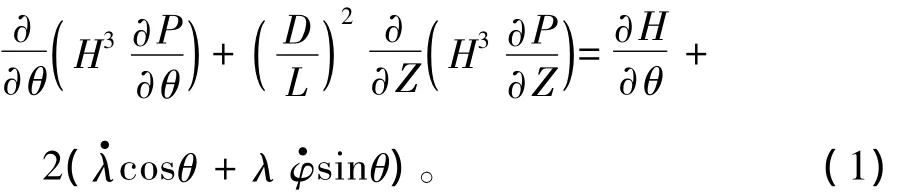
式中:θ为轴承周向坐标;H为油膜厚度;P为无量纲液膜压力;Z为轴承周向坐标;L为轴瓦宽度;D为轴瓦直径;(λ，φ)为轴心无量纲瞬时位置。

采用有限差分法求解二维Reynolds方程，采用较为接近实际情况的雷诺边界条件，求解滑动轴承的液膜压力分布P。由于轴承的动特性，即为轴承液膜压力对位移扰动和速度扰动的导数，所以利用此无量纲雷诺方程，对λ，φ，求其4个偏导，对4个相应扰动压力方程，同样采用有限差分法，可求得4个扰动压力Pλ，Pφ，，分布。通过对4个扰动压力进行积分，即可求得4个无量纲刚度系数和4个无量纲阻尼系数。

式(2)建立在极坐标系(e，φ)上，通过相关坐标转换关系，可得直角坐标系下无量纲刚度系数和无量纲阻尼系。最后通过无量纲与有量纲的转换，就可以得到轴承的4个刚度系数kxx，kxy，kyx，kyy和4 个阻尼系数 cxx，cxy，cyx，cyy。

1.2 滚动轴承动特性

滚动轴承作为一种应用较早，种类较多的轴承，对其的研究，早已开展，并取得了不少成果。对于几种滚动轴承的径向刚度的研究，经过实践的积累，已近得到实践的验证。在此总结几个经典滚动轴承动特性计算公式，为让设计工作者快速得到轴承的动特性提供方便，并为后面软件应用范围的拓展做铺垫。主要涉及的轴承包括:单列向心轴承及向心推力轴承、单列短圆柱滚子轴承、角接触球轴承、圆锥滚子轴承。

2 转子有限元模型建立

本文以某型转子系统为例，其结构简图如图1所示。该型转子系统具有2个弹性支撑和2个叶轮，且支撑形式较为独特，存在多个轴段，相对较为复杂，轴段参数如表1所示。

图1 转子系统简化模型Fig.1 Simplified model of rotor system

表1 轴段参数Tab.1 Shaft segment parameter

已知转轴密度为7 750 kg/m3，弹性模量E=210 GPa，泊松比μ=0.26。针对具体叶轮刚性较好等原因，只考虑其质量、极转动惯量和直径转动惯量。在UG中对叶轮进行参数化实体建模，根据叶轮密度，得到末级叶轮参数为M1=3.068 kg，JZ1=0.008 128 kg·m2，JX1=0.005 373 kg·m2，JY1=0.005 373 kg·m2，首级叶轮参数为M2=2.571 kg，JZ2=0.006 058 kg·m2，JX2=0.004 702 kg·m2，JY1=0.004 702 kg·m2。

轴承是转子系统的一个重要组成部分，需用弹性支撑去模拟。利用自己编制的轴承动特性系数计算软件，可以快速求得转子的2个支撑刚度，K1=4.07 E7 N/m，K2=2.75 E6 N/m，用COMBI214单元模拟轴承，用平面二维的形式去模拟轴承支撑特性;选用 BEAM188单元建立转轴模型;采用MASS21单元建模;最后对转子系统进行网格划分，如图2所示。

图2 模型网格图Fig.2 Grid graph of the model

约束方式，将轴承单元外圈全约束，将轴上连接轴承处节点轴向自由度约束。加载方式，使用OMEGA施加一个转速。同时需要考虑陀螺效应，使用命令CORIOLIS，ON，，，ON打开陀螺效应开关。

3 转子系统多工况仿真

3.1 临界转速分析

坎贝尔图在转子动力学中求解临界转速非常重要。坎贝尔图的横坐标为转速 (激励)，纵坐标为涡动频率，坎贝尔图显示向前涡动 (FW)、向后涡动 (BW)的线，转子系统的临界转速等于坎贝尔图中的频率曲线与附加线F=sω的交点的值。

对转子系统进行临界转速计算，设置分析类型为模态分析，选择QR阻尼法进行求解，所得坎贝尔图和前三临界转速如图3和图4所示。

一般在计算转子临界转速时，通常只考虑同步正向涡动时的振动频率，通常说的临界转速，一般是指同步正向涡动的临界转速。由图3可知，前3阶临界转速其正向涡动与反向涡动，频率相差较小，非常接近，第1，3，5阶频率为反向进动的频率，第2，4，6阶为正向进动的频率，所以得到转子系统的三阶临界转速为6 135 r/min、25 807 r/min、33 870 r/min。实际该转子系统工作转速为2 950 r/min，分析其不会产生共振。

图3 坎贝尔图Fig.3 Campbell diagram

图4 临界转速Fig.4 Critical speed

3.2 不平衡谐响应分析

对于质量为m，偏心距为r，转动角速度为ω的不平衡量，由理论力学知识可知，其离心力F=mrω2。对其进行分解，投影到 xy平面的 Fx=mrω2cos(ωt)，Fy=mrω2sin(ωt)两坐标上。由此可知，不平衡量的激励可以等效为在轴的2个相互垂直的方向上存在一组正弦和余弦的简谐力。

转子系统在两叶轮上同时存在同向的质量为0.001 kg，偏心距为0.005 m的不平衡量。根据上式计算，即在两叶轮处同时施加0.46 N的不平衡力。根据模态分析结果，选择谐响应分析类型，设置研究频率范围为50～600 Hz，分4 400个子步进行求解。由于步长、求解方式、取值大小等问题，其计算结果与上一节中的不平衡响应的计算结果会有一定偏差，也有可能出现峰值之间相差过大，导致图形中较小的峰值看不清，但趋势、共振点等相同。

图5 同向施加不平衡量叶轮1、叶轮2处位移响应Fig.5 Displacement response graph of the impeller 1、2 by the same direction unbalance

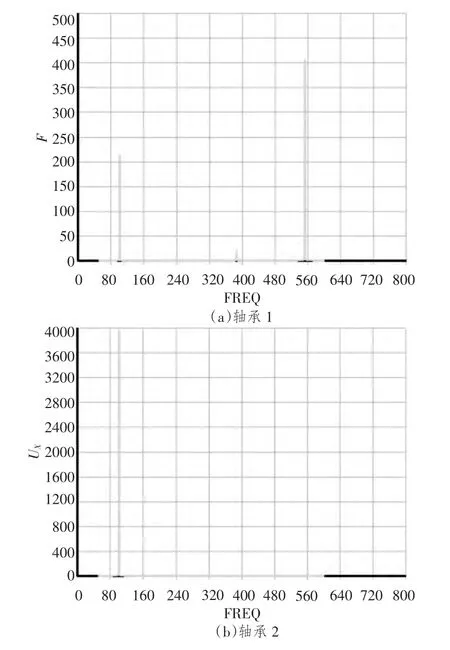
图6 同向施加不平衡量轴承1、轴承2处支反力响应Fig.6 Counterforce response graph of the bearing 1、2 by the same direction unbalance

由图5可知，叶轮在临界转速附近存在较大不平衡位移响应，且在1阶临界转速时最大，叶轮1处最大位移响应1.3 E－3 m，叶轮2处最大位移响应2.1 E－3 m。

由图6可知，轴承在临界转速附近存在较大响应，轴承1在2阶临界转速附近支反力较小，在3阶临界转速附近最大达到400 N;轴承2在1阶临界转速附近最大达到3 950 N左右。

综上所述，当本文转子系统受到一个不平衡量为0.46 N时，其在前3阶临界转速范围内，最大跳动位移在2.1 mm左右，最大支反力在3 950 N左右，但都是短暂的;而且在工作转速附近，其位移跳动较小，基本可以忽略，处于安全状态下，轴承的支反力也处在承载范围之内，所以本转子系统稳定性好，可靠性高。

3.3 瞬态动力学分析

转子系统瞬态动力学，可以研究其在多种工况下的响应。在启动、停车等过程的速度不断变化、在运行过程中出现一个冲击，这类常规情况，都属于需要研究的瞬态动力学内容。设置分析类型为瞬态动力学，通过数组参数定义旋转力－时间的关系。

1)匀加速启动

研究转子系统的启动过程，即研究其按一定加速度加速到工作转速的一段时间内的运动情况。在这类瞬态动力学研究中，一般在叶轮处添加一个不平衡量，方便观察其运行状态。

本文模拟存在一个偏心质量为0.001 kg，偏心距为0.005 m的偏心量，从静止以一定加速度加速到2 900 r/min，加速时间为5 s，观察叶轮位移响应与轴承支反力响应情况。

图7 叶轮1位移响应Fig.7 Displacement response graph of the impeller 1

图8 叶轮2位移响应Fig.8 Displacement response graph of the impeller 2

图9 轴承1支反力响应Fig.9 Counterforce response graph of the bearing 1

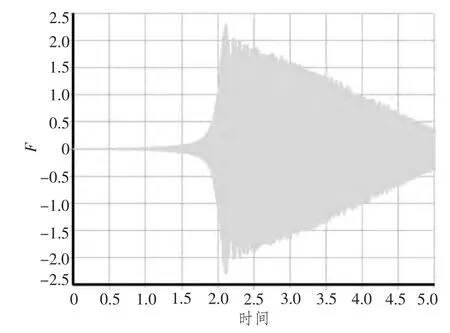
图10 轴承2支反力响应Fig.10 Counterforce response graph of the bearing 2

由图7和图8可知，转子在加速到稳定转速过程中，叶轮处位移响应随时间，在0～1.8 s缓慢增大，在1.8～2.2 s之间急速增大，这也是转子系统启动中振动最大的时间段，而在2.2 s之后缓慢减小，渐渐平稳下降，位移响应值较小，说明了此转子的转动具有稳定性;由图9可知，轴承1的支反力渐渐增大，达到最终恒定转速时，支反力较小;由图10可知，轴承2的支反力，在0～1.8 s缓慢增大，在1.8～2.2 s之间急速增大，而在2.2 s之后缓慢减小，渐渐平稳下降，这与叶轮位移变化趋势较为相同，支反力较小。综合来看，转子整体位移响应与支反力响应，在整个匀加速启动工程中，响应小，较为稳定。

2)冲击载荷

在正常运行状态下，突然受到一个冲击载荷，其在一定时间段内的响应情况。

在Ansys中，本文模拟转子系统在2 900 r/min转速正常运行情况下，突然承受一个幅值为100 N的载荷，作用方向为径向X方向，作用时间为0.001 s，观察其0.02 s内的叶轮位移响应与轴承支反力响应情况。

图11 叶轮1位移响应Fig.11 Displacement response graph of the impeller 1

图12 叶轮2位移响应Fig.12 Displacement response graph of the impeller 2

由图12可知，转子系统在受到一个冲击载荷作用时，其叶轮位移和轴承支反力响应呈现上下波动状，且从冲击刚开始时，冲击方向响应较快;短时间内，转子系统在承受冲击载荷方向上的叶轮位移和轴承支反力响应，明显大于其垂直方向。最终得到转子系统最大位移响应在叶轮1处为2.0 E－5 m左右，最大支反力在轴承1处为100 N左右。这些参数的取得为复杂环境、高精密、高可靠性转子系统的设计提供必要参数帮助。

图13 轴承1支反力响应Fig.13 Counterforce response graph of the bearing 1

图14 轴承2支反力响应Fig.14 Counterforce response graph of the bearing 2

4 结语

本文以某型转子系统为研究对象，首先利用雷诺方程和经验公式计算了其支撑轴承的动特性系数;而后考虑轴承支撑特性和转子陀螺效应影响，利用Ansys对临界转速进行了预测，分析了其在不平衡量、匀加速和冲击载荷作用的多种状态下的响应，说明了该型转子系统在工作转速下不会产生共振，在多种复杂工况下，其响应值较小，转子系统安全可靠。该种分析方法考虑因素全面，更为真实可靠，为旋转机械的设计分析提供指导。

［1］ 袁惠群．转子动力学基础［M］．北京:冶金工业出版社，2013．

［2］ 谢帆，荆建平，万召，等．基于有限差分法的径向滑动轴承油膜压力分布计算［J］．润滑与密封，2012，37(2):12－15．XIE Fan，JING Jian-ping，WAN Zhao，et al．Calculation of oil film pressure distribution of journal bearing based on finite difference method［J］．Lubrication Engineering，2012，37(2):12 －15．

［3］ 刘晓东．汽轮机转子临界转速计算分析［J］．装备制造技术，2009(4):59－61．LIU Xiao-dong．Analysis on critical speed calculation for steam turbine rotor［J］．Equipment Manufacturing Technology，2009(4):59 －61．

［4］ 陈建飞．汽车水泵的强度分析和转子动力学分析［D］．上海:上海交通大学，2012．CHEN Jian-fei．Rotor dynamic and strength analysis of an automobile water pump［D］．Shanghai:Shanghai Jiaotong University，2012．

［5］ MA Hui，WU Zhi-yuan，TAI Xing-yu，et al．Dynamic characteristics analysis of a rotor system with two types of limiters［J］．International Journal of Mechanical Sciences，2014，88(11):192 －201．

［6］ 李玉峰，石广田．600MW汽轮机组基于Ansys的低压转子轴承系统的模态分析［J］．机械设计与造，2007(2):71－72．LI Yu-feng，SHI Guang-tian．The modal analysis based on Ansys of low-pressure rotor-bearing system for 600MW stream turbine［J］．Machinery Design ＆ Manufacture，2007(2):71－72．

［7］ 瓮雷，杨自春，曹跃云，等．某船用发电汽轮机转子模态及动力学分析［J］．舰船科学技术，2014，36(3):62 －67．WENG Lei，YANG Zi-chun，CAO Yue-yun，et al．Research on mode and dynamic characteristics of the marine power generation steam turbine rotor［J］．Ship Science and Technology，2014，36(3):62 －67．

［8］ 张洪才，等．Ansys14．0理论解析与工程应用实例［M］．北京:机械工业出版社，2012．