膜式气囊隔振器帘线缠绕角度研究

金 著，赵应龙，何 琳，张晓平

(1．海军工程大学振动与噪声研究所，湖北武汉430033;2．船舶振动噪声重点实验室，湖北武汉430033)

0 引言

气囊隔振器，又称空气弹簧，作为舰艇减振降噪元器件得到了广泛应用。根据囊体结构，可分为囊式、膜式和混合式气囊3种，其中，膜式气囊有效面积变化率小，固有频率低，在要求隔振器固有频率不高于2.5 Hz时，一般选择膜式气囊［1－4］。

膜式气囊隔振器囊体成型时，需预先做好帘布筒，然后在锥形成型鼓上成型，现有工艺对其帘布层帘线的缠绕角度问题并未深入研究。但膜式气囊在使用过程中，会在橡胶囊体产生较大弯矩、扭矩和囊壁内应力，这些作用力和力矩会使囊体变形，影响系统的正常工作甚至带来严重后果。因此在膜式气囊生产制造时，对帘线采用合理的铺设角度和方式，使其满足力学平衡性的要求，对确保气囊隔振性能和承载能力，减小囊体变形至关重要。所以，对膜式气囊帘线缠绕角度的理论研究十分必要［5－7］。本文通过几何分析和应力计算，推算出帘线的缠绕角和力学平衡角表达式，进而确定了帘线的平衡缠绕角，并提出等效平衡缠绕角的概念，通过有限元仿真对计算结果的正确性和等效平衡缠绕角的存在性进行验证。

1 研究对象简介与建模

1.1 研究对象简介

本文以某典型膜式气囊为研究对象，其样机外观如图1所示。该气囊主要由囊体、盖板和保护法兰组成，气囊气室由橡胶囊体和金属结构封闭而成。橡胶囊体主要由3部分组成:内胶层，帘线层，外胶层。帘线层是主要的承载部件，包在内外胶层之间，分为多层，各层之间严格按一定角度交叉包覆，呈现各向异性的特点［8］，如图2所示。

图1 膜式气囊样机示意图Fig.1 The simple of RSA

图2 帘线缠绕方式示意图Fig.2 Wounding of the cord

1.2 半圆环壳体结构几何建模

由于帘线层的厚度相对气囊囊体的尺寸结构很小，同时囊体的结构、载荷和边界条件都是轴对称的，满足弹性力学中关于薄壳、无矩理论的假定，因此可将囊体作旋转薄壳处理。

气囊囊体模型如图3所示，第1和第3部分分别为圆柱壳，主要承受拉压力;第2部分为一半圆绕中心线旋转一周而成的半圆环壳，受力情况复杂。本文将对第2部分帘线缠绕角度进行分析。取第2部分，建立坐标系，如图4所示。截面半圆半径为r，截面圆心距z轴距离为R(本文研究对象基本尺寸为:R=70 mm，r=19 mm)。φ为r沿半圆环壳圆心线转过角度，θ为R沿z轴转过角度。那么半圆环壳上任意点坐标可由(θ，φ)唯一表示。

故采用参数θ，φ作为变量，用iθ和iφ分别为沿参数曲线θ和φ的单位切向量，并定义从单位切向量iφ转向帘线缠绕轨迹切线方向的有向角α为缠绕角，如图5所示。

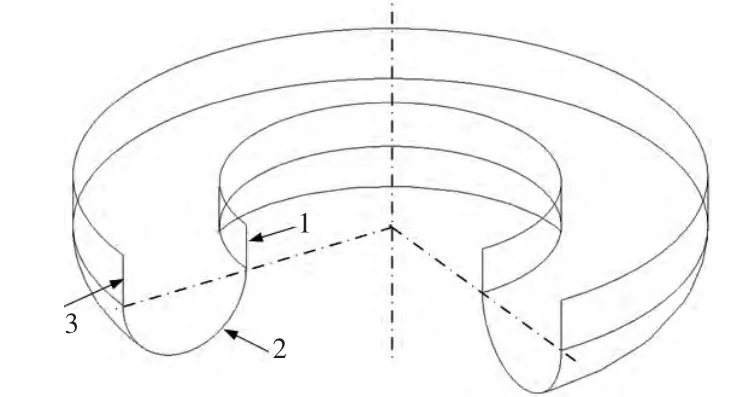
图3 囊体薄壳模型Fig.3 Lamina model of RSA

图4 第2部分坐标系Fig.4 Coordinate system of part 2

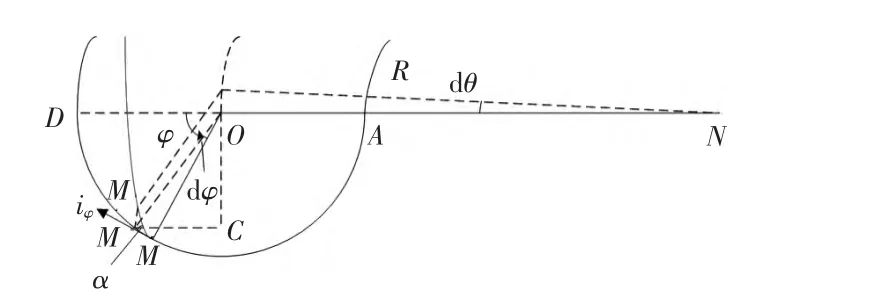
图5 几何分析图Fig.5 Figure for geometrical analysis

半圆环壳壳体管径均匀，帘线在壳体表面缠绕可被认为是一条沿壳体曲面伸展的空间螺旋线的一部分。由图中几何关系易得，半圆环壳体帘线的缠绕轨迹方程为:

式中，

2 帘线平衡缠绕角

2.1 平衡缠绕角推算

由图5易知，当环形壳体半径NO绕z轴转过dθ角度时，帘线对应长度为BB';同样，半圆环半径OB转过dφ角度时，帘线在圆弧截面上对应长度为d B″。由几何关系易知，帘线缠绕角在数值上等于角B'BB″，如图6所示。

图6 缠绕角计算示意图Fig.6 Figure for wound angle calculating

结合图5分析可知:

由此可得帘线缠绕角的正切表达式为:

此外，在囊体半圆环壳面上任意B点处取dθ和dφ单元微元体，其在iθ和iφ方向受到的弹性力P1和P2，环向应力pσm和轴向应力pσn表达式分别为［9］:

其中t为囊壁厚度。则该点处应力合力与iφ的夹角为:

管理会计的主要任务是收集企业在运营中资金方面的信息，整理后进行分析利用，全面地了解经济活动过程，并对企业经济行为作出预测，从而为企业管理层提供有效的服务[1]。而财务会计同样也要搜集相关信息，但信息内容比管理会计更细致、更具体，从而为企业决策层提供信息支持。二者虽然工作重心有所不同，但最终目的都是为管理者提供数据，以便管理者作出更好的决策，为其提供服务的作用是一致的。

由于帘线不承受剪切力，因此点B处帘线的平衡方向与该点处的应力方向重合，即角¯α为力学平衡角。

当囊体充气时，只有帘线所受应力方向与其缠绕方向一致时，才能保持平衡。因此，定义当点B处初始帘线缠绕角α与该点处力学平衡角¯α相等时，即内力恰好落在此时的帘线上，该缠绕角称为气囊的平衡缠绕角。就有等式:

那么，联立式(3)、式(5)、式(6)，可得气囊囊体半圆环壳上的平衡缠绕角的表达式为:

在本文研究对象中，φ角的取值范围是0到π，由此可得φ与α的对应关系，以及帘线在囊体上的理论上的缠绕轨迹，如图7所示。

图7 帘线平衡缠绕角度Fig.7 The cord's equilibrium-wound angle

2.2 等效平衡缠绕角

气囊隔振器囊体的平衡性很大程度上影响了气囊工作的有效时间和性能发挥。在制造膜式气囊时，如果帘线按照上述平衡缠绕角铺设在囊体上，气囊在受内压作用时，帘线恰好承受了囊体的应力，若忽略帘线的受力变形，帘线间夹角将不会发生变化，从而囊体不会发生形变，气囊能达到最佳的平衡状态。但是实际生产过程中，由于生产技术和成本等原因的限制，帘线很难按照图8中所示轨迹准确的进行铺设。

由气囊平衡缠绕角的推算过程易知，在囊体充气状态下，当帘线缠绕角度α大于力学平衡角¯α时，囊体会拉伸以使缠绕角α减小，让帘线受力恢复平衡。反之亦然。因此，在工程上可以在帘线平衡缠绕角计算结果的范围内选定一个合适的等效平衡缠绕角度，将帘线在整个环形囊体上都按照该角度铺设，使囊体的拉伸变形与收缩变形抵消，以保证气囊在该缠绕角度下，充气时囊体具有最佳的平衡性，即囊体变形最小且均匀，从而达到降低成本、简化工艺而不损失性能的目的。

3 有限元仿真分析

3.1 有限元仿真及结果

图10 帘线按30°缠绕角缠绕Fig.10 Cord wounding by the angle of 30°

图11 帘线按34°缠绕角缠绕Fig.11 Cord wounding by the angle of 34°

图12 帘线按35°缠绕角缠绕Fig.12 Cord wounding by the angle of 35°

图13 帘线按36°缠绕角缠绕Fig.13 Cord wounding by the angle of 36°

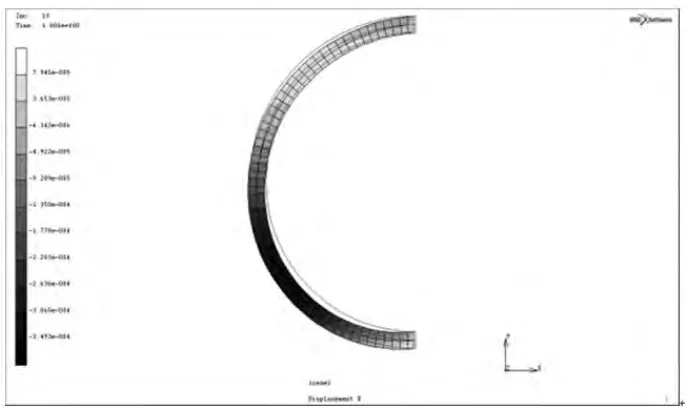
图14 帘线按40°缠绕角缠绕Fig.14 Cord wounding by the angle of 40°

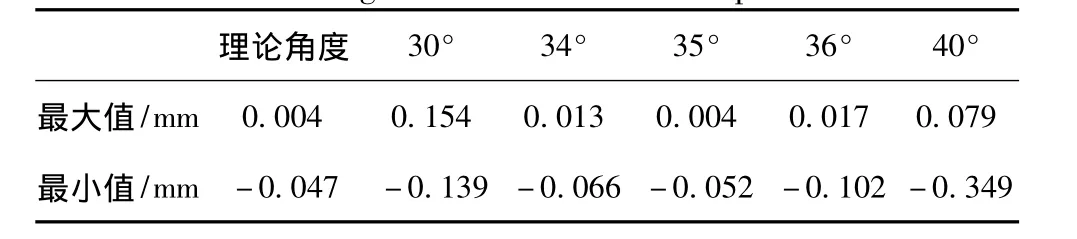
表1 囊体轴向位移值的范围Tab.1 Range of the RSA's axial displacement

3.2 仿真结果分析

由6次仿真结果的对比可以看出:

当帘线按照本文推算的平衡缠绕角缠绕时，气囊在充气后囊体沿轴向变形范围在－0.047～0.004 mm，变形量最小。而且由图9可见内外侧囊壁变形均匀，囊体具有最佳的平衡性，验证了本文的理论推算结果。

当帘线按照固定度角度缠绕时，在缠绕角为35°时，囊体变形在－0.052～0.004 mm，变形量最小，且内外侧囊壁变形均匀，和囊体按照平衡缠绕角缠绕时基本等效，验证了等效平衡缠绕角的存在性。

当帘线缠绕角大于35°时，囊体内侧呈现膨胀变形，外侧收缩变形;缠绕角小于35°时，囊体呈现内侧收缩变形，外侧膨胀变形。囊体的变形趋势与前文所述一致。而且由图10易见，缠绕角度偏离35°越多，囊体变形量越大，变形越不均匀。

4 结语

通过对某型膜式气囊囊体半圆环壳部分进行分析，研究了平衡缠绕角的理论，提出了相关公式，并通过仿真试验验证其有效性。

1)推算出囊体帘线的平衡缠绕角计算公式。帘线按照平衡缠绕角缠绕时，囊体能达到平衡状态;

2)提出了帘线的等效平衡缠绕角概念。按照该角度缠绕帘线，在保证气囊囊体在受内压作用时具有极佳的平衡性的前提下，简化了制作工艺。

本文计算结果可为膜式气囊设计与施工中的参数选取提供理论依据，为膜式气囊囊体加工过程中帘线层制作生产工艺的改进提供理论指导。

［1］ 郝玉密．低频高载荷空气弹簧研究［D］．南京:南京航空航天大学，2007．HAO Yü-mi．Research on air spring of low-frequency and high-load［D］．Nanjing:Nanjing University of Aeronautics and Astronautics，2007．

［2］ 朱石坚，何琳．船舶减振降噪技术与工程设计［M］．北京:科学出版社，2002．ZHU Shi-jian，HE Lin．Ship vibration and noise decreasing technology and engineering design［M］．Beijing:Science Press，2002．

［3］ 赵应龙，吕志强，何琳．JYQN舰用气囊隔振器研究［J］．舰船科学技术，2006，28(2):89 －92．ZHAO Ying-long，LV Zhi-qiang，HE Lin．Study of pneumatic vibration isolator of type JYQN［J］．Ship Science and Techology，2006，28(2):89 －92．

［4］ 赵应龙，何琳，吕志强，等．回转型气囊隔振器的冲击刚度研究［J］．舰船科学技术，2006，28(2):113－116．ZHAO Ying-long，HE Lin，LV Zhi-qiang，et al．Study of shock stiffness of convoluted pneumatic vibration isolator［J］．Ship Science and Techology，2006，28(2):113－116．

［5］ 顾太平，何琳，赵应龙．囊式空气弹簧平衡性分析［J］．机械工程学报，2011，47(3):69 －72．GU Tai-ping，HE Lin，ZHAO Ying-long． Equilibrium performance analysis for bellows type air spring［J］．Journal of Mechanical Engineering，2006，28(2):113 －116．

［6］ 张立国，张嘉钟，贾力萍，等．空气弹簧的现状及其发展［J］．振动与冲击，2007，26(2):146 －150．ZHANG Li-guo，ZHANG Jia-zhong，JIA Li-ping，et al．Future and development of air springs［J］．Journal of Vibration and Shock，2007，26(2):146 －150．

［7］ 叶伟，何琳，帅长庚，等．肘形橡胶软管平衡性能研究［J］．船舶力学，2009，13(2):285 －289．YE Wei，HE Lin，SHUAI Chang-geng，et al．Study on equilibrium performance of rubber hose elbow［J］．Journal of Ship Mechnics，2009，13(2):285 －289．

［8］ 张俊玲，王浩宇．初始内压和帘线间距对膜式空气弹簧横向刚度特性影响的有限元分析［J］．橡胶工业，2013，60(4):233－238．ZHANG Jun-ling，WANG Hao-yu．Effect of initial internal pressure and cords distance on lateral stiffness of rolling lobe air spring by using finite element analysis［J］．China Rubber Industry，2013，60(4):233 －238．

［9］ 帅长庚．肘形挠性软管设计理论、试验方法及工艺研究［D］．武汉:海军工程大学，2005．SHUAI Chang-geng．Study on the designing principle，Test Method and Processing Technology of Flexible Curved Hose［D］．Wuhan:Naval University of Engineering，2005．