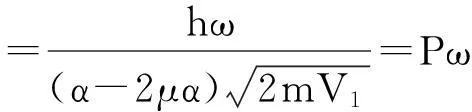附加δ势垒对一维半无限深势阱影响的研究

唐义甲，韩修林

(阜阳师范学院 物理与电子工程学院，安徽 阜阳 236037 )



附加δ势垒对一维半无限深势阱影响的研究

唐义甲，韩修林

(阜阳师范学院 物理与电子工程学院，安徽 阜阳 236037 )

摘要：通过对添加δ势垒的一维半无限深势阱的薛定谔方程进行求解，得到了粒子运动的波函数和能级的相关公式，分析发现，δ势垒的添加以及它的强度与位置的变化对能级都有影响。对比不含δ势垒的一维半无限深势阱的能级，探究δ势垒的添加对原能级产生的影响，并利用Mathematica作图来直观显示这一影响。

关键词：δ势垒；一维无限深势阱；能级

薛定谔方程大致可以分为两类：定态薛定谔方程和含时薛定谔方程。定态薛定谔方程的研究主要利用椭圆偏微方程理论和变分法理论，这方面的结果非常丰富[1-2]。含时薛定谔方程在上世纪70年代以后，随着调和分析手段的引入而发展迅速，尤以著名数学家J. Bourgain，T. Tao，C. Kenig和F. Merle等人的工作备受瞩目[3-4]。

由于δ函数的特殊性，δ(x)势在原子、分子、固体及多体等问题中均有广泛应用[5-6]，而在量子力学定态薛定谔问题中引入δ(x)势却鲜有报道[7-8]。本文在已有严格解的一维半无限深方势阱内引入δ(x)势， 采用理论分析、数值计算与作图显示相结合的方法，对δ势引起的能级及波函数进行修正。

1附加δ势的半无限深方势阱

设质量为m的粒子，作一维运动，在半无限深方势阱中附加δ势后，如图1所示，势能为

(1)

其中，μ是描述势阱位置的无量纲参数，取值区间为(0，1)。

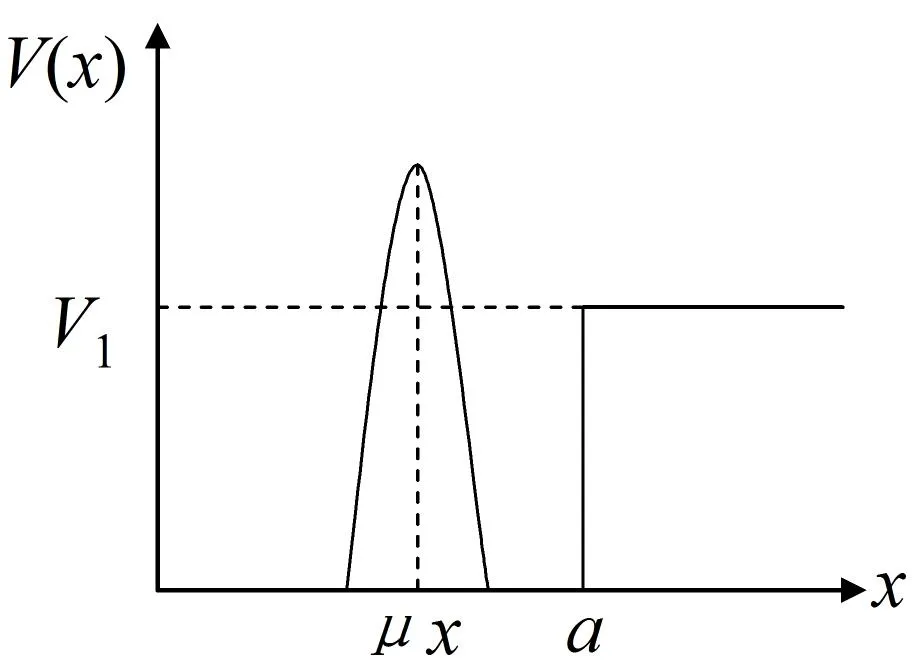
图1　附加δ势垒的一维半无限深势阱

粒子的波函数与能量满足定态薛定谔方程：

(2)

由于势能不连续，定态薛定谔求解可分为四个区域：

(3)

由于束缚态粒子的能量有限性，在区域Ⅰ内波函数应为零，即波函数ψ0(x)=0。

在区域Ⅱ，Ⅲ内，定态薛定谔方程为

(4)

上式可以简化为

(5)

其中，

(6)

在区域Ⅳ内，定态薛定谔方程为

(7)

由束缚态条件知E

ψ″-β2ψ=0

(8)

其中

(9)

由波函数的连续性，得到在边界x=0处

ψ1(0)=ψ0(0)=0

(10)

x=μa是方程(5)的奇点，ψ′(μα)不连续，利用波函数连续条件并对(5)式积分，得

ψ2(μa+0)+ψ1(μa-0)= ψ(μa)

(11)

在x=a处，由波函数一阶导数连续，可得到

(12)

2半无限深方势阱中附加δ势的粒子的波函数与能级

2.1定态波函数

方程(5)的通解为

ψ1(x)=Asin(kx)+A′cos(kx)

(14)

考虑到边界条件(10)，可得当A′=0，所以区域II内

ψ1(x)=Asin(kx)

(15)

由方程(8)，得到区域Ⅳ内的波函数为

ψ3(x)=Ce-βx+Deβx

(16)

当x→∞时，波函数应有限，所以

D=0

(13)

ψ3(x)=Ce-βx

(17)

方程(5)在区域Ⅲ内的通解为

ψ2(x)=Bsin(kx+φ)

(18)

结合衔接条件(12)得

kcot(kx+φ)=-β

(19)

为简单起见，假定λ=0，则衔接条件(11)变为

ψ′(μα+0)=ψ′(μα-0)

(20)

势阱过渡为半无限深方势阱，如果存在波函数在μα处为零，则(20)同样适用于λ≠0，因此假定先波函数在μα处为零，采用迭代法求解，易解得

(21)

A，C可由波函数连续性条件和归一化条件确定，参数k,β与能量有关，其他参数可由(19)和(20)式确定。

2.2定态能量

2017年，联盟成员立项或在研创新项目39项，形成自主知识产权多项，包括发明专利9项，实用新型专利4项，软件著作权18项。形成技术标准多项，包括行业标准2项，地方标准3项，企业标准2项，团体标准14项。

将(21)式代入条件(11)，得到

(22)

(23)

(24)

进一步化简得

(25)

或

(26)

令k(α-2μα)=ω，则k=ω/(α-2μα)，(26)式可化为

(27)

解超越方程(27)可求出各能量，结果表明,若势阱内有束缚态能量是量子化的，势阱内至少有一个束缚态的基态能的条件是

作出函数y=|sinω|和函数y=Pω的图像，其交点即为超越方程(27)的解

图2　超越方程(27)图解示意图

3运用mathematica作图显示δ势垒的影响

添加δ势垒后，能级的相关公式为

(29)

令n=log2H，取K1= 10不变， 运用mathematica求解。

3.1势垒位置的影响

当n为0，1，2，3，……，10，μ分别取0.1到0.9之间的数值时，计算K的数值解(只取基态值)，结果如图3所示。

图3　K随μ的变化曲线

由图3可以看出：当n=0时H=1，即(势垒很低时，μ值的变化对基态能级的影响并不大，随着n的增大，μ值的影响也越明显，当μ处于0.55左右时对基态能级的影响最大，两侧逐渐减小。

3.2势垒强度的影响

当μ分别取0.1 ，0.2，……，0.9之间的数值，n为0，1，2，3，……，10时，计算K的数值解(只取基态值)如图4所示。

图4　K随n的变化图形

由图4知,在一定范围内K值随着n值的增大而增大，而当n增大到某个值或减小到某个值时K值达到稳定不再变化。K的最小值与μ无关约为2.85，而K的最大值随着μ的不同而有所不同。

4特殊情形

4.1情形一

当n→-∞时H→0，此时模型变为一维半无限深势阱。由上文讨论的不含势垒的一维半无限深势阱的情况可知,与能级有关的表达式为

(36)

同样，取K1= 10，求得基态时K≈2.852 3，这与图4中n→-∞时所得结果一致。

4.2情形二

表1

又由一维半无限深势阱能级的相关公式得kcot[k(1-μ)a]=-κ，即无量纲化后为

同样，取K1= 10，运用mathematica求得μ取不同的值时对应的基态K值如表2所示。

表2

综上所述，当μ取不同的值时，整个一维半无限深势阱中当n→∞时对应的基态K值如表3所示。

表3

这与图4中n→∞时所得结果一致。

当μ=1/2，V1=∞，即K1=∞时，我们的模型成为中央有δ势垒的无限深势阱，将条件代入(29)式得到

(33)

(34)

(35)

这个结果与文献[7]所得结果完全一致。

5结束语

通过理论推导与数值分析，研究了在添加δ势垒的一维半无限深势阱中运动的粒子的能级的影响因素，得到了该势能下的波函数和能级的相关公式。对于给定势垒高度K1的一维半无限深势阱，δ势垒的添加会使束缚态能级的量值增加，能级个数减少；势垒的强度与位置对能级都会产生影响，当势垒处于势阱中心偏右位置时能级最大，在K1=10的情况下，μ≈0.55，δ势垒的强度H越大，位置的影响越明显；当δ势垒的位置一定时，δ势垒的强度H越大，能级越大。当H→∞时势阱分裂为一维无限深势阱和一维半无限深势阱两部分，并且由这两部分求的基态能级与本文公式(29)中当H→∞时求得的结果一致；适当选取参数发现文献[5-7]中的结果都是本文结果的特例，这表明了本文结论的普遍性和正确性。

参考文献:

[1] M. Willem. Minimax theorems[M]. Basel Boston Berlin: Birkhaüser，1996.

[2] I. Kuzin， S. Pohozaev. Entire solutions of semilinear elliptic equations[M]. Basel Boston Berlin: Birkhaüser，1997.

[3] T.Tao，M.Visan，Xiaoyi Zhang.The nonlinear Schröinger equation with combined power-type nonlinearities[J].Communications in Partial Differential Equations， 2007，32(8):1281-1343.

[4] L.Ma，J.Wang. Inhomogeneous problem for the Ginzburg-Landau equation on two dimensional compact manifolds[J]. Dynamics of Partial Differential Equations， 2010， 7(2):175-185.

[5] 曾谨言．量子力学[M].北京：科学出版社，1982:69.

[6] 史守华.量子力学考研辅导教材[M]. 北京：清华大学出版社，2003:4-5.

[7] 李明明，陈岗．无限深方势阱附加δ势后的定态解[J].山东师范大学学报，2004，12(4):96-97.

[8] 井孝功，陈硕，赵永芳．方形势与δ势解的关系[J].大学物理，2004，12(12):18-20.

[5] 钱伯初，曾谨言．量子力学习题精选与剖析[M] .2版. 北京：科学出版社，1999:2-4.

[6] 周世勋．量子力学教程[M] .1版.北京：高等教育出版社，1979:19-20.

[7] 朱文熙，王玉平．对称双方势阱无简并[J] .大学物理，1999，2(2)：33.

[8] 尹健武，冯杰，陈娇. 一维高低不对称方势阱问题的数值方法[J] .黄冈师范学院报，2005，12(6):26-29.

Research on the Effects of Additional Delta Barrier to One Dimensional Semi-infinite Deep Potential Well

TANG Yi-jia，HAN Xiu-lin

(School of Physics and Electronic engineering，Fuyang Teachers College， Fuyang 236037， China)

Abstract:By adding the delta barrier of one dimensional semi-infinite deep potential well，and solving the schrodinger equation, the related formula of particle movement of wave function and energy level are obtained. Through analysis we found that the delta barrier to add and its change on the energy level of the position and strength are affected. Contrast does not contain the delta barrier in one dimensional semi-infinite deep trap energy level. In addition, we explore the delta barrier to add to the impact of the original energy level, and use the Mathematica graphic visual indication to this effect.

Key words:δ potential barrier, one dimensional semi-infinite deep potential well, energy level

文章编号：1007-4260(2015)03-0060-04

中图分类号：O469

文献标识码：A

DOI：10.13757/j.cnki.cn34-1150/n.2015.03.017

作者简介：唐义甲，男，安徽枞阳人，硕士，阜阳师范物理与电子工程学院助理实验师，研究方向为非线性光学材料、高能粒子束辐照改性及防护。

基金项目：国家自然科学基金项目( 11273008) ，阜阳师范学院教学研究项目(2012JYXM61)，(2013ZYJS08)和阜阳师范学院基础教育研究项目(2012JCJY21)。

收稿日期：2015-01-11

网络出版时间：2015-8-25 15:40网络出版地址：http://www.cnki.net/kcms/detail/34.1150.N.20150825.1540.017.html