“生动”教学模式下线性代数的教学设计与实践
——以线性方程组为中心展开
2015-03-11刘薇
刘 薇
(湖南财政经济学院 基础课部,湖南 长沙 410205)
“生动”教学模式下线性代数的教学设计与实践
——以线性方程组为中心展开
刘 薇
(湖南财政经济学院 基础课部,湖南 长沙 410205)
摘要:通过对线性代数课程内容的优化,以学生为主体,采用“生动”的教学方法进行线性代数教学,实践证明,“生动”教学模式不仅解决了线性代数课时少、内容多的问题,而且营造了生动活跃的线性代数课堂,激发了学生学习线性代数的积极性,提高了学生分析问题和解决问题的能力。
关键词:线性代数;生动;教学实践
线性代数作为大学数学课程中的一门主干课程,具有较强的逻辑性、抽象性以及广泛的实用性。自各高等院校开设线性代数课程以来,大多数的教学以理论讲授为主,而学生大多数是被动的学习,现阶段高校教学改革后,线性代数课程目标的取向是帮助学生追求智力的卓越发展,数学能力和数学素养的提升[1]。“教师讲授,学生听记”的教学模式,达不到理想的教学效果,也无法适应学生的学习要求。针对线性代数课程课时少,内容多的问题,对线性代数现有的教学内容进行优化,突出以学生为主体,将“生动”的教学模式实践于教学,营造活跃的教学课堂氛围,既带动了学生学习线性代数的积极性,又提高了教师教授线性代数的教学质量。
1线性代数教学内容的优化
目前我国线性代数[2]课程的教学内容主要有行列式、矩阵、线性方程组、向量组的线性相关性、特征值与特征向量及二次型。初学者对分散的块状结构感到线性代数知识点较多,内容不连贯,学习起来毫无头绪,因此教师在教学过程中需要把握线性代数的核心思想,理清课程的脉络,使学生对课程有一个整体的把握。
线性代数课程有“形散而神不散”的特点,虽然看起来内容较为松散,但实际上章节之间密切相关。教学实践发现,线性方程组及矩阵的初等行变换是线性代数的核心思想。以线性方程组作为突破口进行教学,是一个行之有效的方法[3]。优化线性代数教学内容即先由线性方程组,给出行列式、矩阵、向量和向量组,再由矩阵的初等变换给出矩阵(向量组)的秩、向量的线性相关性、线性方程组的解等理论和概念。因此以线性方程组为主线构建的教学体系逻辑性强,便于问答式、探究式“生动”教学法的实施。线性代数课程内容优化体系结构如图1所示。

图1“线性代数”内容优化体系结构图
2“生动”教学法在课堂中的实践
“生动”的教学模式在线性代数课堂中的具体实践过程如下:布置研究课题,学生自学、查找资料、初步学习分析;解决研究课题,学生提问,教师引导答疑;归纳总结,学生归纳与总结、教师评价与完善。
“生动”教学模式的施教过程中要求教师注意以下几点:
(1)学生是教学的主体,教师是引导者。首先教师应本着“以学生为主体,学生为中心”的教学观念进行施教。其次,要构建适宜的教学情景,激发学生探究问题的积极性,引导学生提出问题、分析问题、解决问题。
(2)师生换位提问,鼓励学生敢于提出问题,充分挖掘学生的创新潜能,培养学生的创新意识。
(3)课堂小结和课题总结,注意问题的补充。
首先,教师将第一个课题进行示范,即行列式,提交课题报告并在课堂上讲解课题主要内容及典型例题。然后,将班级学生分为四大组,每一组分配一个课题,要求本组学生共同完成此部分课题的研究,并提交课题报告,分节分点讲解课题研究的主要内容。最后,教师作点评、总结和考核。
背景题设:引入线性方程组
(*)
学生示范课题1矩阵及其运算、逆矩阵的求解、矩阵的初等变换、矩阵的秩,初等变换法求解矩阵方程
(1)矩阵定义及其运算
背景题设中线性方程组的系数矩阵记为:


(2)求解矩阵A的逆矩阵
法一:伴随矩阵法,即
因为|A|=-5≠0,则A可逆,且

法二:用矩阵的初等变换求逆矩阵,即

(3)矩阵的初等变换
B为A的行阶梯形矩阵。

C为A的行最简性矩阵,也为A的标准形。
(4)求矩阵的秩
解因为A→B,有r(A)=r(B),所以由(3)可知A的秩为3。
(5)用初等变换法求解矩阵方程
令X=(x1,x2,x3)T,B=(-2,1,0)T,则此线性方程组可表示为矩阵形式:AX=B,解AX=B,则X=A-1B。
用初等变换法求解矩阵方程AX=B,即

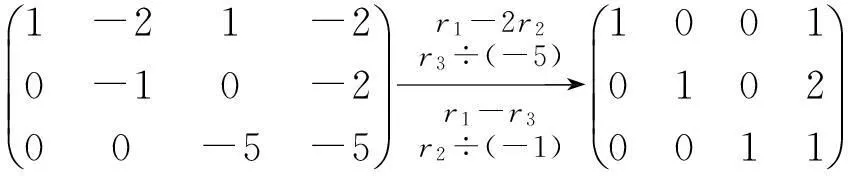
(6)内容补充及拓展

教师围绕学生所提出的问题对该课题进行补充、小结,带动学生思考以下问题:矩阵的运算中,乘法不满足交换律和消去律;方阵才有幂,行列式和其对称矩阵;矩阵A可逆的充要条件是|A|≠0;初等变换法可以求矩阵的秩;求逆矩阵;解矩阵方程,即矩阵的初等变换不改变行(列)之间的线性关系。
学生示范课题2向量、向量组的线性相关性、向量组的秩、向量空间、线性方程组解的结构。
背景题设中线性方程组的矩阵形式记为:AX=B,其导出的齐次线性方程组记为AX=0。
线性方程组向量的表现形式:
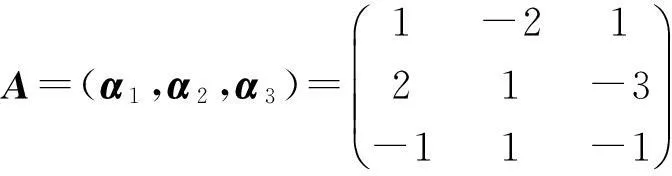
(1)向量组的线性相关性
讨论α1,α2,α3,β的线性相关性,即对由α1,α2,α3,β生成的列向量组做初等行变换,化其为行阶梯型矩阵(或行最简形矩阵),则求得其线性相关性,一个极大线性无关组和向量组的秩。
解(α1,α2,α3,β)=

(2)向量组的秩
rank(α1,α2,α3,β)=3,即为α1,α2,α3,β的极大无关组所含向量的个数。
(3)线性方程组解的结构
求线性方程组
(**)
及其导出的齐次线性方程组的通解。



ξ1=(-1/2 -1/2 1 0 0)T,ξ2=(0 -1 0 1 0)T,ξ3=(2 -3 0 0 1)T
故齐次方程组的通解为
x=c1ξ1+c2ξ2+c3ξ3,(c1,c2,c3∈)
求原方程的特解:令x3=x4=x5=0,得
η*=(-9/2 23/2 0 0 0)T,故原方程的通解为
x=c1ξ1+c2ξ2+c3ξ3+η,(c1,c2,c3∈)。
由上题易知,若ξ1,…,ξn-r是Ax=0的基础解系,η*是Ax=b的一个解,则非齐次线性方程组Ax=b的通解可表示为x=c1ξ1+c2ξ2+…+cn-rξn-r+η*,c1,c2,…,cn-r∈。
(4)内容补充及拓展
学生示范课题2中,学生围绕教师布置的背景题设方程组(**),讲解线性方程组的向量表示形式、向量的线性相关性、向量组的秩、矩阵与向量组秩的关系和向量空间及其基与维数。对线性方程组用消元法和矩阵的初等变换进行求解。课堂上学生提出问题:a.齐次线性方程组和非齐次线性方程组的解与其系数矩阵或增广矩阵之间的关系;b.向量组线性相关性的理解;c.极大无关组与基的联系与区别;d.如何求矩阵或向量组中的一个极大无关组,如何求向量空间中的一个基。
教师围绕学生所提出的问题对该课题进行补充、小结,带动学生思考:a.讨论向量组的线性相关性即讨论其齐次线性方程组有无非零解;b.由于矩阵或向量组的初等变换保持了向量间的线性无关性和线性相关性,即可用其求解线性方程组的解、向量组的线性相关性、向量组的秩和一个极大无关组;c.若把向量空间V看作向量组,则V的基就是向量组的极大无关组,V的维数就是向量组的秩;d.通过矩阵的运算给出两个基的变换公式和向量在两个基下的坐标变换公式;e.齐次线性方程组与非齐次线性方程组解的结构。
3考核测评方法
“生动”的教学模式要求教师对学生进行考核时,不单凭一张期末试卷来决定学生对该课程学习程度。我们采取的考核测评分为四个部分来进行加权求和,即课题研究报告20%,课堂表现10%,能力测试20%,期末试卷分数50%。其中课堂表现包括两方面的内容:一是课堂中对该课题的讲解及讨论;二是对线性代数的知识点总结。能力测试包括两方面内容:一是课后作业情况;二是教师布置几道具代表性的习题进行随堂测试情况,这种考核方式可以督促学生有意识地培养自己解决实际问题的能力,提高自己的创新意识和能力。
4结束语
运用文章中的“生动”教学模式对本院《线性代数》课程进行施教,实践发现,“生动”教学模式不仅解决了《线性代数》课程课时少、内容多的问题,而且为师生营造了生动活跃的线性代数课堂,激发了学生学习线性代数的积极性,提高了学生分析问题和解决问题的能力。通过对所教的6个班级进行比较分析,其中3个班级采取“生动”教学模式,另外3个班采取“传统授教”模式。期中期末进行该课程考核,将成绩进行比较发现,“生动”教学模式授课班级学生成绩平均分超过“传统授教”模式班级10分以上,且不及格率几乎为零。同时在全校学生的评教活动中,该教学模式受到学生的欢迎。“生动”教学模式激发了学生探索问题的能力,使之运用此方法进行其它课程的学习,大大提高了学生的学习能力。因此,“生动”教学模式不仅培养了学生的思维,而且促进了大学生创新素质的发展,并全面提高高校教学质量。
参考文献:
[1]COMAP.数学的原理与实践[M].申大维,方丽萍,叶其孝,译.北京:高等教育出版社, 1998.
[2] 吴赣昌. 线性代数[M].4版.北京: 中国人民大学出版社, 2011.
[3] 何立国, 施武杰. 以线性方程组为中心展开线性代数课程的教学[J]. 大学数学, 2009, 25(6): 203-206.
Teaching Design and Practice of Linear Algebra Based Vivid Teaching Mode——To Linear Equation Group as the Center to Carry Out
LIU Wei
(Department of Basic courses, Hunan University of Finance and Economics, Changsha 410205, China)
Abstract:Through the optimization of the linear algebra curriculum content, we take the student as the main body. Using the teaching method of "vivid" linear algebra teaching, practice proved that the "vivid" teaching model can not only solve the linear algebra class is small, the contents of many problems, but also create a linear algebra class lively and active, and stimulate students to learn actively linear algebra, and improve students' ability to analyze and solve problems.
Key words:linear algebra, vivid, teaching practice
文章编号:1007-4260(2015)03-0110-04
中图分类号:O13
文献标识码:A
DOI:10.13757/j.cnki.cn34-1150/n.2015.03.029
作者简介:刘薇,女,湖南岳阳人,硕士,湖南财政经济学院基础课部讲师,研究方向为统计、代数分析。
基金项目:湖南省高等学校科研基金项目(12C0565)和湖南财政经济学院青年教师科研基金项目(Q201401)。
收稿日期:2014-12-14
网络出版时间:2015-8-25 15:40网络出版地址:http://www.cnki.net/kcms/detail/34.1150.N.20150825.1540.029.html
