一分数阶四翼超混沌系统的同步控制
2015-03-11杨志宏屈双惠吴淑花于津江
杨志宏, 屈双惠, 吴淑花, 于津江
(石家庄学院 物理与电气信息工程学院,河北 石家庄 050035)
混沌控制和混沌同步理论在保密通信、信号处理等领域有着极其广泛的应用,而分数阶混沌系统由于其具有更大的密钥空间而在保密通信方面具有更高的使用价值,因此,在实际应用中研究分数阶混沌系统的特性及其同步具有十分重要的意义。
已有不少学者开始研究分数阶系统的同步问题,但对于分数阶超混沌系统的同步问题的研究却很少。文献[1]虽然研究了分数阶超混沌Chen系统和R¨ossler系统的异结构同步问题,但其提出的超混沌系统的每个方程中最多含有1个二次非线性交叉乘积项。本文构建的分数阶四维超混沌系统,系统的每个方程中都含有1个三次非线性交叉乘积项,具有真正的四翼混沌吸引子,由于四翼混沌吸引子的系统信号具有更宽的频谱带宽,因此在信息加密技术中具有更重要的使用价值。利用非线性反馈控制法,通过控制反馈控制增益的取值范围实现了响应系统与驱动系统的同步,实现了对该分数阶四翼超混沌系统的混沌同步,通过数值仿真验证了该方法的有效性[2-4]。
1 系统模型
本文构建的四翼超混沌系统整数阶形式为:其中,a、b、c、d、e为实常数。
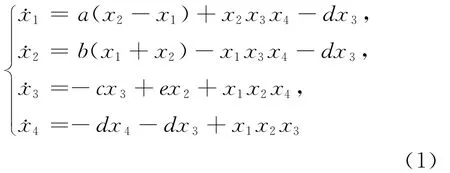
当参数a=50,b=7,c=13,d=12,e=8时,系统的Lyapunov指数分别为:
LE1=4.055 3, LE2=0.317 4,LE3=-20.913 7, LE4=-51.458 7。指数LE1和LE2均为正,系统具有超混沌的特征[5]。图1所示为该系统的混沌吸引子,从图1中可以看到,系统产生了穿越上下吸引域界限的对角混沌吸引子,上下混沌吸引子与对角混沌吸引子融合成一个真正的四翼混沌吸引子。

图1 整数阶系统相图
该系统的分数阶形式为:
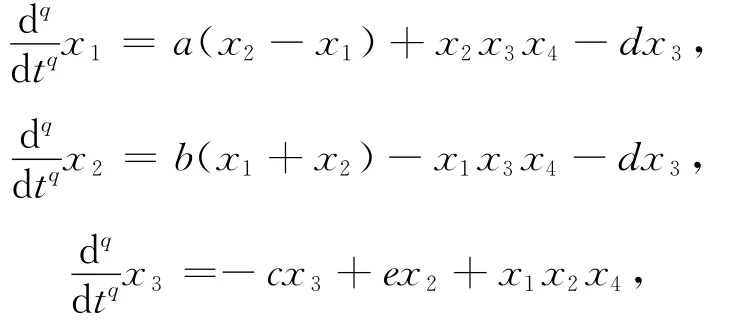
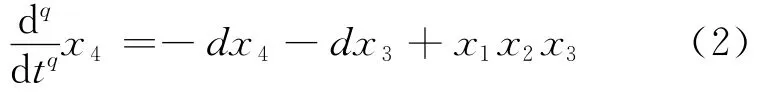
取如下参数:
a=50,b=7,
c=13,d=12,e=8。
当阶数q=0.95时,系统相图如图2所示。
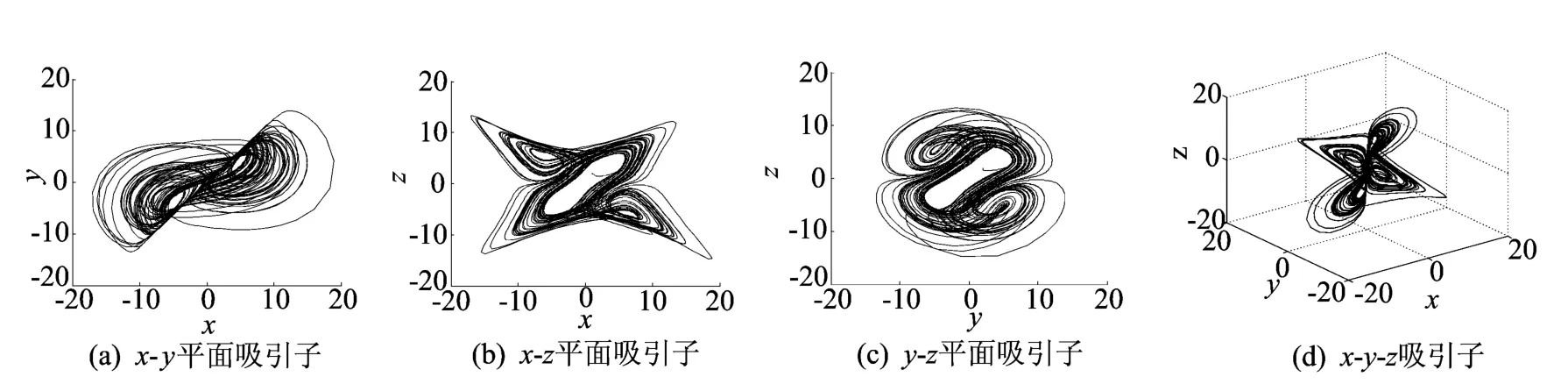
图2 分数阶系统相图
2 频谱分析
2.1 整数阶系统频谱分析
图3a、图3b所示为整数阶三维Lü系统和四维Chen系统[6]的频谱图。
图3c所示为整数阶四翼混沌系统的频谱图,这里只给出了x分量。
由图3可以看出,四翼混沌系统的频谱带宽比Lü系统和Chen系统的频谱带宽大很多,这在信息加密技术中具有更重要的应用价值。
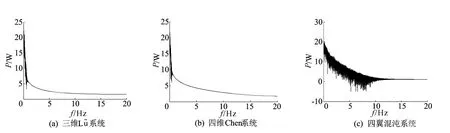
图3 整数阶系统功率谱
2.2 分数阶系统频谱分析
图4所示为当阶数q=0.95时上述3个系统在分数阶形式下的频谱图。由图4可以看出,对于分数阶形式,四翼混沌系统的频谱带宽仍远大于Lü系统和Chen系统的频谱带宽,在信息加密技术中起重要作用。
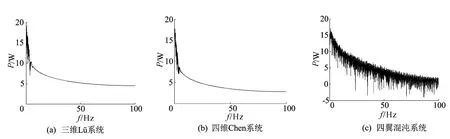
图4 q=0.95时分数阶系统功率谱
3 系统的混沌同步
3.1 理论分析
随着混沌同步研究的发展,人们提出了多种不同的混沌同步方法,如线性或非线性反馈同步、耦合同步、自适应同步、投影同步等[1,6-9]。以下将分数阶系统(2)作为驱动系统,其复制系统作为响应系统,并将控制器u=[u1,u2,u3,u4]T施加在响应系统上,利用非线性反馈控制实现同步的方法来实现两系统的混沌同步。
则有驱动系统方程为分数阶系统(2),响应系统方程为:
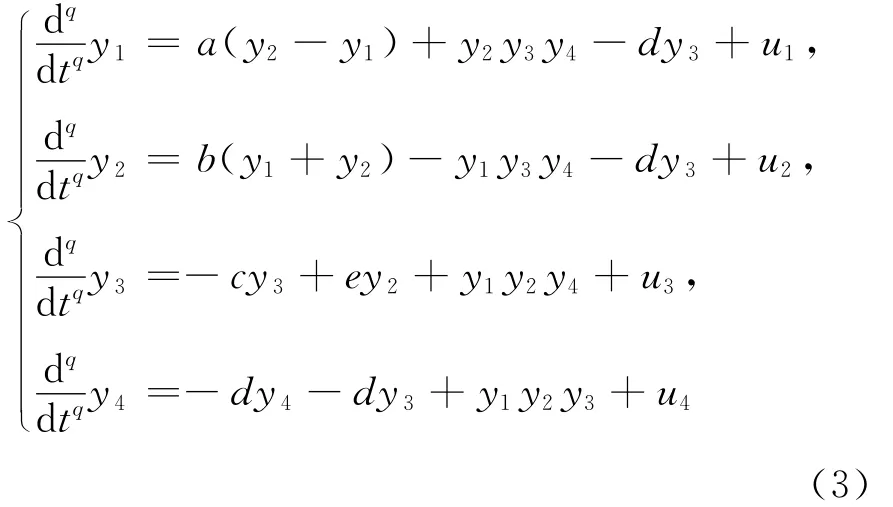
为了获得能够实现驱动系统与响应系统同步的控制函数,令状态误差信号为:
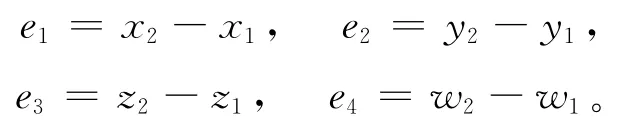
(3)式减(2)式可得到误差系统为:
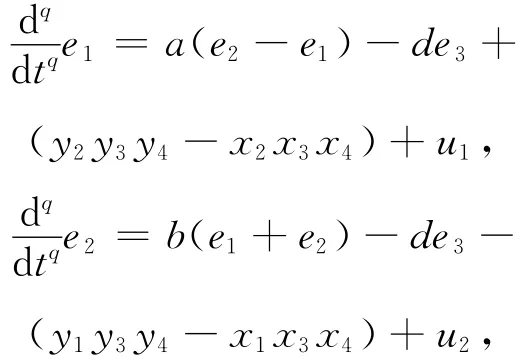
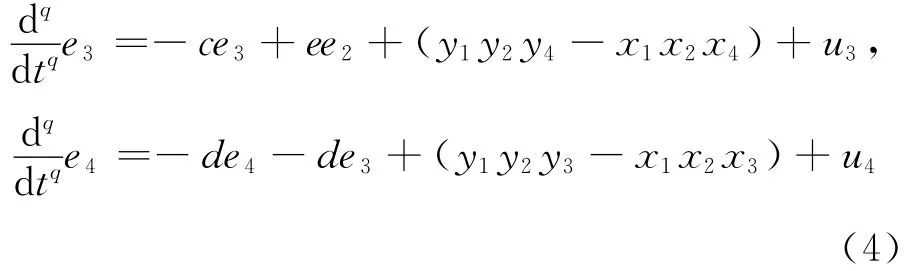
选择控制函数为:
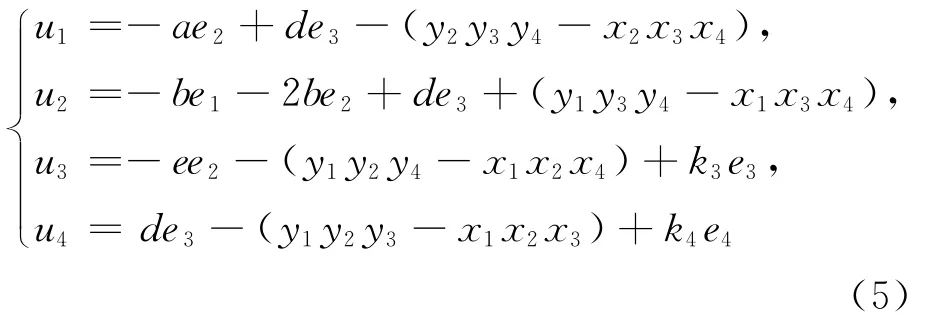
其中,k3、k4为反馈控制增益,其值待定。
下面根据系统的稳定性理论确定反馈控制增益k3、k4的取值范围,从而实现驱动系统(2)与响应系统(3)的混沌同步。将(5)式代入(4)式并将方程组写成˙e=A(t)e的形式,得到误差系统方程的矩阵形式为:
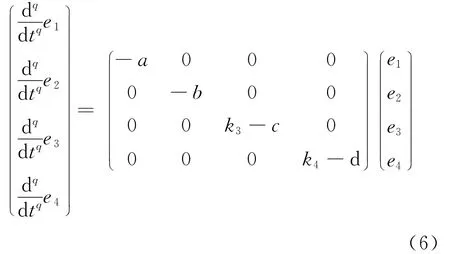
由(6)式可知,误差系统的平衡点在误差变量的零点处。依据非线性系统的线性化稳定性定理,矩阵A(t)为时变矩阵,即
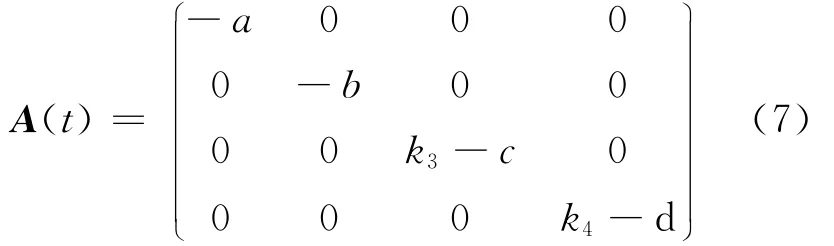
系统处于混沌状态时,系统变量只能在一定的吸引域内发生变化,此时A(t)对所有的t都是有界的。
从(7)式可以看出,当反馈控制增益k3、k4的取值范围满足k3<c,k4<d时,该矩阵的所有特征值都具有负实部,此时线性系统˙e=A(t)e的零解都达到渐进稳定,即误差系统(6)在其原点处实现渐进稳定,驱动系统(2)与响应系统(3)在非线性反馈控制作用下达到同步。
3.2 数值模拟
取阶数q=0.95,选取系统参数a=50,b=7,c=13,d=12,e=8,初始点x1(0)=1,x2(0)=1,x3(0)=1,x4(0)=1,y1(0)=2,y2(0)=2,y3(0)=2,y4(0)=2。用 Matlab软件数值模拟驱动系统(2)和响应系统(3)的同步过程,得到同步误差曲线如图5所示。由图5可以看到,在控制器的作用下,误差变量e1、e2、e3、e4都在短时间内稳定在零点,2个系统实现了同步。
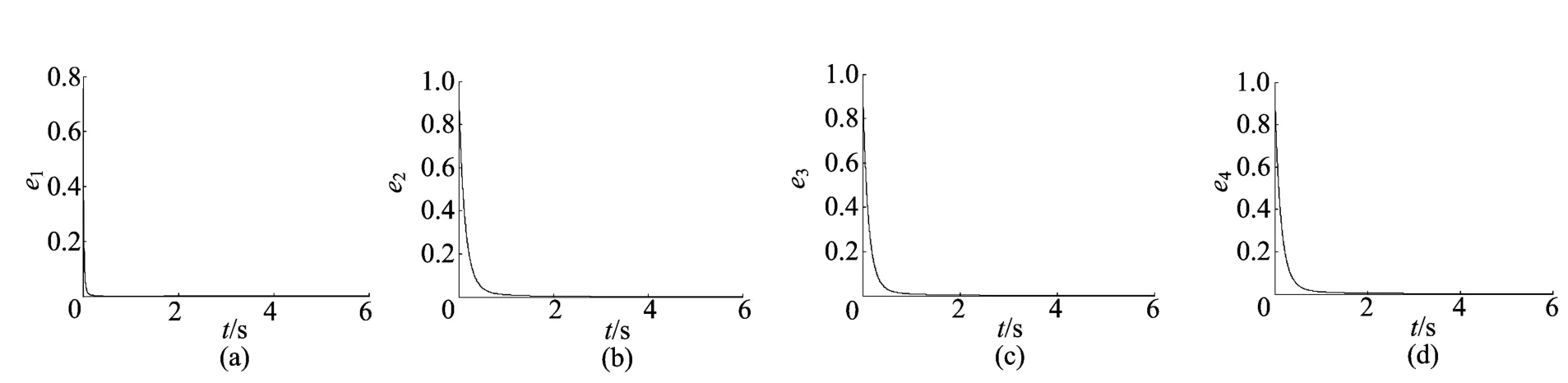
图5 同步误差e1、e2、e3、e4 随时间t的变化曲线
4 结束语
本文提出的分数阶四翼超混沌系统,系统信号具有较宽的频谱带宽,在信息加密工程中具有应用价值。利用非线性反馈控制法,实现了对该分数阶四翼超混沌系统的混沌同步,控制器的结构简单易于实现。下一步的主要研究方向是利用非线性系统进行保密通信的硬件实现。
[1] 李 东,邓良明,杜永霞,等.分数阶超混沌Chen系统和分数阶超混沌R¨ossler系统的异结构同步[J].物理学报,2012,61(5):050502.
[2] 鲍慧玲,薛 华.一个三维四翼混沌系统的分岔分析及其电路实现[J].合肥工业大学学报:自然科学版,2014,37(2):155-158,208.
[3] 刘崇新.一个超混沌系统及其分数阶电路仿真实验[J].物理学报,2007,56(12):6865-6872.
[4] 孙克辉,任 健,丘水生.分数阶统一系统的混沌动力学特性[J].华南理工大学学报:自然科学版,2008,36(8):6-10.
[5] 张晓丹,李志萍,张丽丽.一类基于奇异值分解的指数计算方法[J].北京科技大学学报,2005,27(3):371-374.
[6] 蔡国梁,黄娟娟.超混沌Chen系统和超混沌R¨ossler系统的异结构同步[J].物理学报,2006,55(8):3997-4004.
[7] 马铁东,江伟波,浮 洁.基于比较方法的分数阶混沌系统脉冲同步控制[J].物理学报,2012,61(9):090503.
[8] 徐 江,蔡国梁.一个新的不确定超混沌Lorenz系统的自适应同步[J].江苏科技大学学报,2009,23(3):271-273.
[9] 胡建兵,章建国,赵灵冬.间歇同步分数阶统一混沌系统[J].物理学报,2011,60(6):060504.
