基于服务模式切换的数据中心能耗最小化问题研究
2015-03-11魏振春韩江洪
魏振春, 朱 赛, 卫 星, 韩江洪
(1.合肥工业大学 计算机与信息学院,安徽 合肥 230009;2.安全关键工业测控技术教育部工程研究中心,安徽 合肥 230009)
云计算被认为是下一代的IT服务模式,受到学术界和工业界的巨大关注[1]。社会对云计算需求的不断扩大需要构建规模巨大的数据中心,而维护其运行需要大量的能量[2]。如何高能效地运行数据中心是一个亟待解决的问题。
目前,分布式并行计算系统的能耗优化管理技术主要包括3类:关闭/休眠技术(resource hibernation)、电压动态调整技术(dynamic voltage scaling,DVS)和虚拟化技术(virtualization)[3-4]。
关闭/休眠技术的相关研究通常是针对计算机或处理部件的关闭/休眠时机进行设定或预测。但是对于包含有众多计算资源的云计算系统,如何根据单位时间到达的任务量决定要关闭的计算机数量以及关闭哪些计算机等问题,都给关闭/休眠技术赋予了新的研究难题。
电压动态调整技术的核心思想是通过动态调整电压使同一处理器具有不同的功率/性能“挡位”,用不同的“挡位”来处理不同类型、不同计算量的任务,在降低执行能耗的同时又保证了执行性能。但是在云计算系统中,电压动态调整技术遇到以下几个问题:① 计算任务到达的随机性,难以预测下一个到达任务的类型;② 即使知道了任务类型,也很难准确分析该任务所适合的处理器电压“挡位”;③ 电压动态调整技术主要是用来降低计算机中处理器的能耗,对整台计算机或整个云计算系统的能耗优化存在一定的局限性。
虚拟化技术,特别是深层次的虚拟化本身也要付出高昂的效能代价,因为虚拟化技术是对底层硬件部件到高层服务应用的层层虚拟,每一级的虚拟都造成了效能的损失。
上述3种策略在节能方面都有一定的作用,但也有各自的不足,同时其节能效果也不明显,因此本文针对云计算系统中的能耗浪费问题,从服务模式切换入手找出数据中心中的最优离线调度算法。
1 模型建立
服务器的能耗包括操作能耗和切换能耗[5]。分配有工作负载的服务器处于活跃模式,没有工作分配的服务器处于节能模式。为了使操作能耗最小化,服务器应尽可能处于空闲模式,这种操作称为“关闭”。同时因为存在切换能耗,为了使总能耗最小化,服务器状态切换不应太频繁。因此,需要一种平衡使总能耗最小。
研究具有N台同构服务器(每台服务器具有相同容量C,即在一个时隙内服务器可承担的最大工作数)的数据中心[6]。每个时隙开始时会估算平均负载并为每台服务器调整负载分配。定义时间片t时的负载为λt,考虑T周期内,初始工作负载为λ0,结束工作负载为λT;服务器具有相同的操作能耗函数f(λ),其中λ∈[0,C]是分配的工作负载,并且有相同的切换能耗系数βon≥0、βoff≥0来打开或关闭服务器。服务器数量充足,即λt≤NC。对于每个时隙t,需要确定活跃服务器的数量xt和分配给第i台服务器的负载λt,i,其中

记xt等于正的λt,i的数量,因而有:
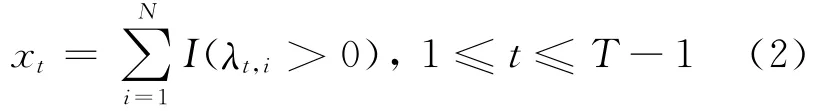
其中,I(e)表示如果事件e发生,值为1,否则为0。因为λ0=λT>0且根据(1)式有:
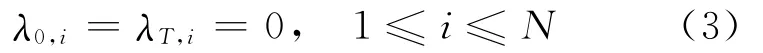
并且根据(2)式有:

定义:
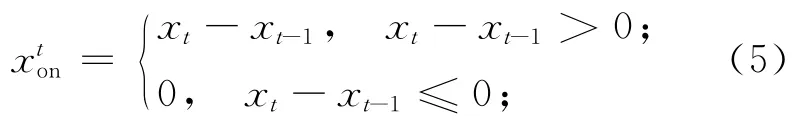
其中,t∈[0,T];xton为在t时切换到打开状态(即从空闲模式切换到活跃模式)服务器的数量。同时定义:

其中,t∈[0,T];xtoff为t时切换到关闭状态(即从活跃模式切换到空闲模式)服务器的数量。因此可以得到:
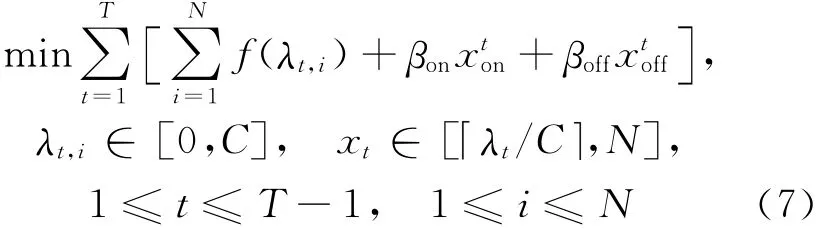
其中,λt,i为连续变量为整数变量;T、N、βon、βoff、λt、C 和λT,i等于0;x0=xT=0。
由于(7)式中双重叠加过于烦琐,下面将通过等量替换和数学推导来对其进行简化。
首先定义标准化工作负载和一个新的能耗函数为:

其中,xλ,t为λt工作负载下的最小服务器数(不一定为整数);θt,i为t时隙下第i台服务器所承担的工作负载占其所能承受最大负载的百分比;g(0)=0。
将目标函数(7)式重新写作:
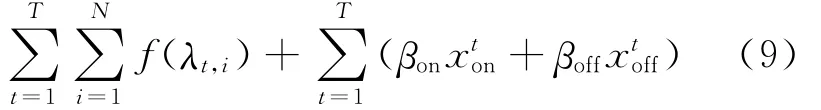
其中,第1部分为所有服务器的操作能耗;第2部分为服务器的切换能耗。根据(8)式,第1部分重新改写为:


由于g(0)=0,且根据(3)式λT,i=0,操作能耗可以重写为:
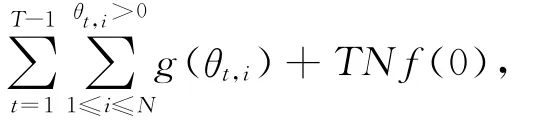
其中,TNf(0)为一个常数,可以省略。根据(4)式x1off=0且xoTn=0,得到βoffx1off=0和βonxoTn=0。切换能耗可以改写为:
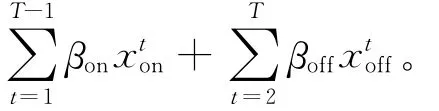
由于g(x)是凸函数,对于每个处于活跃状态的服务器,当θt,i=xλ,t/xt时,对xt>0有:

于是目标函数的操作能耗可以重写为:

得到简化后的目标函数为:

2 模型最优特性分析
2.1 无切换成本的最优解
首先考虑特殊情况,βon=βoff=0(无切换成本)。这种情况的结论可用于研究βon,βoff≥0时(一般情况下)的最优算法。记

由于g(x)、F(x)都是凸函数,因而操作能耗可写为:
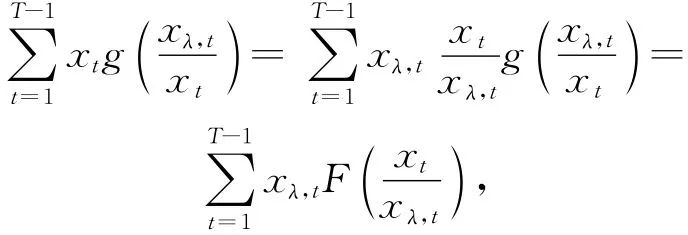
进而问题变为:

其中,xt为整数变量;T、xλ,t、N 为常量。这个问题可以拆成对于每个xt的T-1的子问题。对于xt的子问题,1≤t≤T-1,则有:
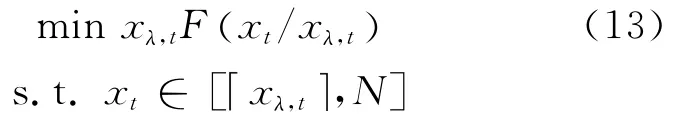
其中,xt为整数变量;xλ,t、N 为常量。
由于F(x)是凸函数,可以定义一个真值xF使在 x∈ [1 ,N/xλ,t]区 间 内F(x)最 小,因 而,xFxλ,t使F (x/ xλ,t)在x∈[xλ,t,N]内最小。有最优解,在约束条件下是绑定于xλ,t和N 的整数,特别有以下3种情况:① 当xFxλ,t≤xλ,t,则最优解;② 当xFxλ,t=N,则最优解为xt*=N;③ 当xλ,t<xFxλ,t<N,则最优解为xFxλ,t或xFxλ,t。
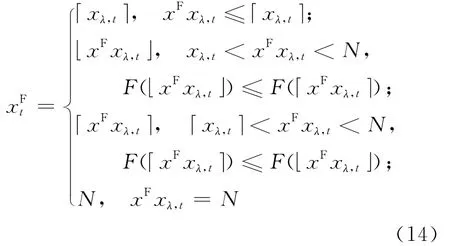
于λt,所以只取决于λt,以上解均为在线解。
2.2 最优特性分析
一般地,即βon,βoff≥0时,考虑和
以上引理可以通过反证法证明。
根据以上引理,最优解可描述为:必然存在一个整数τ≥0,使,因为在此周期内)曲线跟随)曲线,所以称[0,τ]是“跟随”周期。
最优解示例如图1所示,其中τ=1,跟随区间为[0,1]。如果,由引理1可知,在和之间。根据引理2,可得到,直到这条平整线在时间处与曲线相交,即和在的不同侧,则称[τ+1,]为“平周期”;图1中,=3时平区间为[2,3]。根据引理3必是和之间的值。如果,可以得到下一个跟随区间和下一个平周期。否则将得到下一个平周期,如图1中的下一个平周期[4,5]。由此将会得到许多跟随周期和平周期,其中最后一个周期是跟随周期,因为在t=T时刻,图1中得到的最后一个跟随周期为[6,9]。

图1 最优解示例
根据以上3条引理,可得到从t=T到t=0时间段内最优曲线)与曲线的关系。首先得到一个跟随周期t∈[τ,T],当t=T时,;若,则,直到这条平整线与)曲线相交于点。[,τ-1]为一个平周期。同理得到下一个跟随周期和平周期,最后的周期是跟随周期,因为在t=0时。
3 基于整数规划的最优算法
考虑λt(1≤t≤T)值是已知前提下设计的最优算法[8]。
3.1 基于动态规划的最优离线算法
设计一个基于动态规划的最优离线算法,它伴随着一个递归过程。定义一组子问题:在给定工作负载λτ和指定结束xt=h≥xλ,t的条件下,考虑关于τ∈[0,t]上最小化整体能耗的子问题。定义这个子问题的整体最小能耗为c(t,h),其中t为系统运行到的当前时刻,h为在系统运行到t时刻时处于活跃状态的服务器数量。对于目标问题,在(4)式中有xT=0,因此目标问题的整体最小能耗定义为c(T,0)。
3.1.1 证明c(T,0)的递推公式
根据(14)式和λT=0,有,则定义t1为使(15)式成立的最小值。

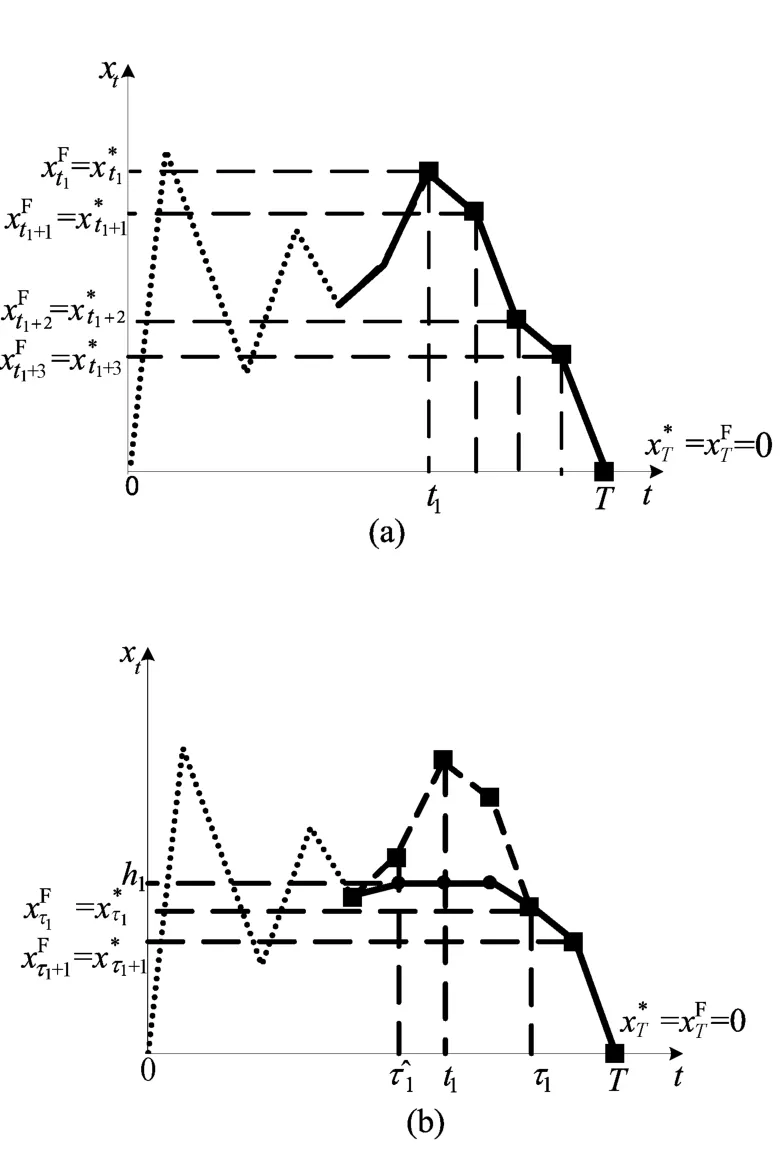
图2 计算c(T,0)时存在的2种情况
如果是情况①,整体能耗的最小值在t∈[0,t1]内为。对于t∈[t1,T],有,因而可以计算出整体能耗(不包括t1时刻的操作能耗,因为此能耗已在中被计算过)。
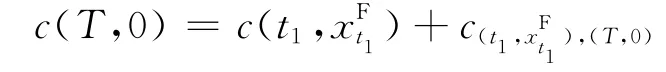
如果是情况②,定义1是t∈[1,t1]上的最大值,故

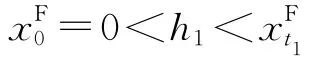
由于,所以此1一直存在;进而可证明在t∈[1+1,τ1-1]上。因此根据引理5有。但是由于,根据引理4(或引理6)可能不等于,也就是说平周期在1处结束,则可以认为(16)式中定义的1是高度为h1的平高线与曲线的交点。x?1的值固定为h1时,在区间上的整体能耗最小值为。由于在上且t∈[τ1,T]上,可计算出上的整体总能耗(不包括τ1时的操作能耗,因为此能耗已在c(1,h1)中被计算过),此能耗计作c(?1,h1),(T,0),因而有:
c(T,0)=c(1,h1)+c(1,h1),(T,0)。同时考虑2种情况,则有:
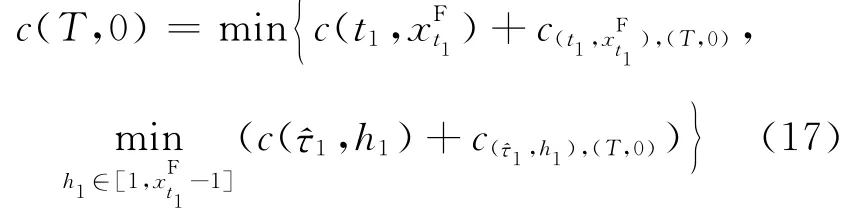
实际可以将情况① 和② 整合,因为前者是后者的特殊情况。由于1是根据定义的,且在(16)式中等于t1,则(17)式可以写成:

(18)式给出了若干基于一些c(1,h1)值计算c(T,0)的递推方法。
3.1.2 计算(18)式中特定的c1,h1)
定义t2为使(19)式成立的最小值,即

在c1,h1)的最优解中必会出现以下2种情况之一:① 对于所有的,如图3a所示;② 存在一个τ2∈[t2+11-1]和,使得对于t∈[τ2,1-1]有,且,如图3b所示。
如果是情况①,xt2固定为时,在t∈[0,t2]内总能耗的最小值为。由于在t∈[t2,1-1]上且1<h1,可以计算出t∈[t2,1]上的总能耗(不包括t2时刻的操作能耗,此能耗已在)上被计算过)。

图3 计算c1,h1)时存在的2种情况

如果是情况②,可以证明对于任意的h2>都不能产生出最优解。由于,定义2是[1,t2]上的最大值,使得:

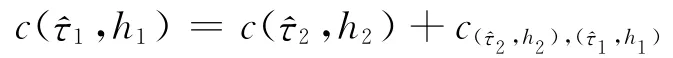
综合以上2种情况得:
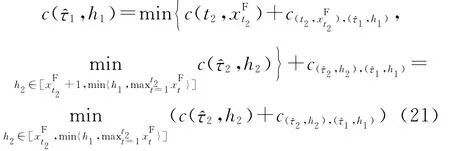
(21)式给出了一个基于c(2,h2)值计算c1,h1)的递推方法,其中h2和2已通过(20)式被定义。
3.1.3 其余步骤
若一些c2,h2)的值被确定,(21)式给出的计算c1,h1)的递推公式可以继续递推过程。当需要确定在时ck,hk)的值时,过程终止,并且可以发现。对于这种情况,很容易证明在t∈[1,-1]上c(,hk)的最优解是,且,因为此解使操作能耗和切换能耗同时最小。求出此解的总体能耗,由此得到c(,hk)值,终止递推过程。
3.2 消除递推过程
首先假设在c(T,0)的计算过程中所有的c(t,h)值都是确定的,整个递推过程需要得到一些c(t,h)的值。t∈[1,t1]满足以下3种情况中的一种:或。因此,对于一个特定的t,如果,则不用计算任何c(t,h)的值;如果,需要计算h∈上c(t,h)的值;如果,需要计算上c(t,h)的值。算法如下:
(3)对于(t=1;t≤U1;t++),若,计算c(t,h),,其中[1,t-1],且。
(4)对于(t=U1+1;t≤UK;t++),若,根据给定的c(·,·)计算c(t,h),其中h∈],如(17)式;若,根据给定的c(·,·)计算c(t,h),其中如(20)式。
(5)根据给定的c(·,·)和(17)式计算c(T,0)。
记Li和Ui分别为第i时刻的局部最小和最大点,则有和。假设有K个局部最大点,则有K-1个局部最小点,且0<U1<L1<…<Lk-1<Uk=t1<T。考虑被这些极点分割出的小的时间周期,对于第1个周期t∈[1,U1],根据最优算法,h可以是[1,]中的任意值,且每个h对应唯一一个t′,因此t∈[1,U1]上要计算的c(t,h)的数目为。对于第2个周期t∈[U1+1,L1],根据最优算法,h可以是]范围内的任意值,且每个h对应唯一一个t,因此t∈[U1+1,L1]上要计算的c(t,h)的数目为。同理,t∈[Uk-1+1,Lk-1]上是;上是。于是c(t,h)要被计算的总次数为:)+…++。可见这仍是离线算法的空间复杂度。
在计算c(t,h)过程中,具有不同高度的平周期。由于h在[1,N]范围内,这些高度最大个数为N,因此,计算c(t,h)的过程具有O(N)复杂度,所以总体复杂度O(KN)O(N)=O(KN2),其中,K<T为t∈[1,T]中局部最大点的数目。
4 数值分析及结果
仿真平台使用C#开发,根据设定的服务器数量和时间片数随机生成工作量,并通过最优离线算法给出服务器最优配置策略。采用文献[9]中的能耗定义,操作能耗函数为:
f(λ)=λmax {1/(1-λ)-1.5,0}+1,
切换能耗系数为βon=βoff=6,服务器容量C=1,工作量λt的取值范围为[1,N]。
设定时间片数T=100、服务器数N=100,得到图4所示的2组计算结果。
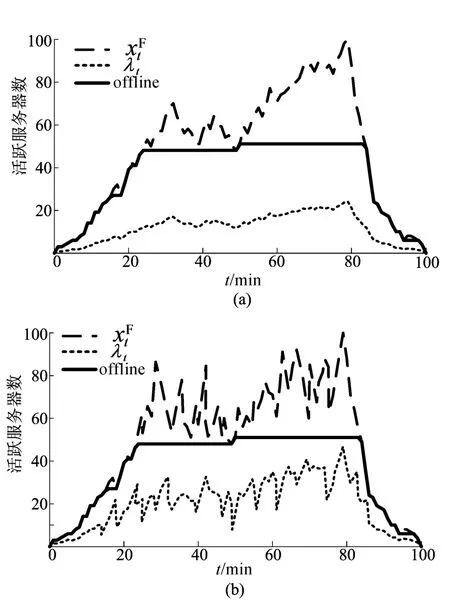
图4 不同负载变化情况下活跃服务器数
图4a中工作量变化比较平稳,图4b中工作量变化幅度较大。
由图4可以看出,在工作量不同的情况下,都能够通过本文算法得到更加平稳的活跃服务器曲线,有效减少了服务器之间的切换量。
每个时间片结束时对应的能耗曲线如图5所示。由图5可以看出,使用离线算法后,数据中心服务器能耗明显降低,通过对不同负载变化情况对比可知,当工作量变化幅度较大时,离线算法的优化效果更为明显。
图6所示为平稳工作负载和波动工作负载2种情况下总能耗及各种情况下切换能耗和操作能耗所占比例,可见负载波动较大情况下,经离线算法优化后切换能耗减少更为明显。

图5 不同负载变化情况各时间片能耗曲线

图6 不同情况下的能耗比例
5 结束语
本文研究了通过调节服务器模式切换来最小化数据中心的能耗并提高数据中心的服务质量。首先,建立了数据中心能耗最小化模型,包括操作能耗和切换能耗;然后分析了最优解的性质,并将这些性质应用到最优算法的设计中,得到了一个基于动态规划的离线算法,进而得到具有多项式复杂度的最优离线算法。此算法不但降低了算法的空间复杂度,同时符合活跃服务器数量需为整数的要求。本文研究的是已知工作负载前提下的最优算法,可为未知负载算法的研究提供参考。
[1] Barroso L A,H¨olzle U.The case for energy-proportional computing[J].IEEE Computer,2007,40(12):33-37.
[2] Li J,Shuang K,Su S,et al.Reducing operational costs through consolidation with resource prediction in the cloud[C]//IEEE International Symposium on Cluster Computing and the Grid.IEEE,2012:793-798.
[3] Beloglazov A,Buyya R,Lee Y C,et al.A taxonomy and survey of energy-efficient data centers and cloud computing systems[J].Advances in Computers,2011,82(2):47-111.
[4] Gandhi A,Gupta V,Harchol-Balter M,et al.Optimality analysis of energy-performance trade-off for server farm management[J].Performance Evaluation,2010,67(11):1155-1171.
[5] Guenter B,Jain N,Williams C.Managing cost,performance,and reliability tradeoffs for energy-aware server provisioning[C]//International Conference on Computer Communications.IEEE,2011:1332-1340.
[6] Guo Y,Member S,Fang Y.Electricity cost saving strategy in data centers by using energy storage[J].IEEE Transactions on Parallel and Distributed Systems,2013,24(6):1149-1160.
[7] Garey M R,Johnson D S.Computers and intractability;a guide to the theory of NP-completeness[M].San Francisco:W H Freeman and Company,1990:204-215.
[8] Lin M,Liu Z,Wierman A,et al.Online algorithms for geographical load balancing[C]//International Green Computing Conference.IEEE,2012:1-10.
[9] Lin M,Wierman A,Andrew L L H,et al.Dynamic rightsizing for power-proportional data centers[J].IEEE/ACM Transactions on Networking,2013,21(5):1378-1391.
