一类非线性兰彻斯特方程的相轨线分析

谢英超， 程 燕， 李文涛

（陆军军官学院 基础部，安徽 合肥 230031）

0 引 言

兰彻斯特方程是在1914年由英国工程师F.W.Lanchester创立的［1］，是动态描述作战对抗性态势的定量工具，已广泛应用于作战进程的定量研究与分析中［2］。针对不断变化的战争形态，许多军事运筹学工作者对兰彻斯特方程进行了诸多改进，并提出了诸如兰彻斯特混合律［3］、偏微分战斗模型［4］、随机格斗模型［5］及多兵种协同作战模型［6］等新型作战理论。

随着信息化战争时代的到来，对高技术条件下的信息化战争的分析与研究已成为当前作战理论研究的热点之一。传统的兰彻斯特方程已无法描述信息因素对现代战争进程的影响，因此需要对兰彻斯特方程做进一步的改进［7］。文献［8］通过引入战场感知系数和信息优势系数研究了反映信息对战争影响的广义兰彻斯特作战模型，具体公式如下：

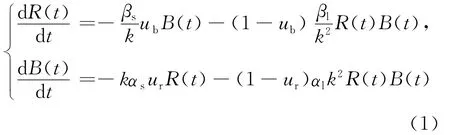
其中，R（t）、B（t）分别为t时刻红、蓝方兵力数量；αs、βs分别为直接火力时红、蓝方每个战斗成员在单位时间内平均毁伤对方战斗成员的数量；αl、βl分别为面火力时红、蓝方战斗成员的作战效能；ur∈（0，1）、ub∈（0，1）分别为红、蓝方的战场感知系数；k＝ur／ub为红方对蓝方的信息优势系数。

文献［9］通过引入信息作战能力系数、战场暴露系数，研究了现代化战争条件下的非线性兰彻斯特战斗模型，具体公式为：

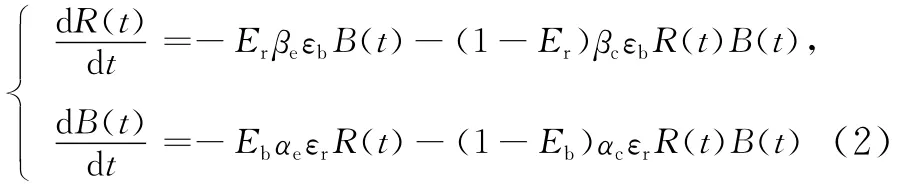
其中，R（t）、B（t）分别为t时刻红、蓝方兵力数量；αe、βe分别为红、蓝方的暴露毁伤系数；αc、βc分别为红、蓝方的隐蔽毁伤系数；εr、εb分别为红、蓝方的信息作战能力系数；Er∈［0，1］、Eb∈［0，1］分别为红、蓝方的战场暴露系数。

（1）式、（2）式均可以转化为：

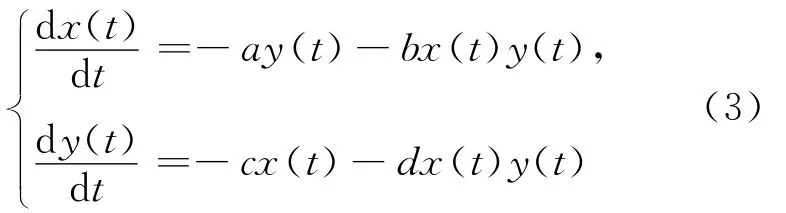
其中，x（t）、y（t）分别为t时刻红、蓝方兵力数量；a、b、c、d分别为对应的正系数。

微分方程组（3）式为非线性自治系统，其解析解难以求得，而相轨线分析是研究非线性自治系统的一类行之有效的方法，已被广泛应用于广告学［10］、传 染 病 模 型［11］、生 态 系 统［12］及 磁 学［13］等领域。本文将对（3）式进行相轨线分析，并结合（1）式，将所得结果应用于分析作战进程和预测战斗结局中。

1 主要结果

假设（3）式满足如下初始条件：

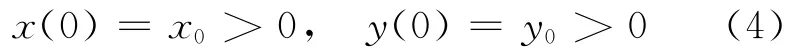
考虑到问题研究的实际意义，有x（t）≥0，y（t）≥0，结合（3）式有（x，y）∈U＝［0，x0］×［0，y0］。设战斗结束时间为T，即x（T）≥0，y（T）＝0或x（T）＝0，y（T）≥0，则t∈I＝［0，T］。令Ω＝I×U，则（t，x，y）∈Ω。

定理1 （3）式在U内具有唯一的奇点P（0，0），且该奇点为（3）式的鞍点。

证明 根据奇点的定义，（3）式的奇点满足：

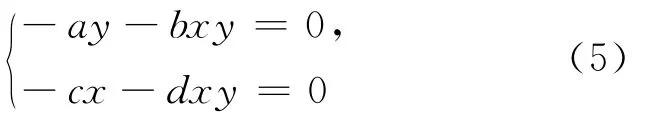
求得奇点坐标为 P（0，0），Q（－a／b，－c／d），而P∈U，Q∉U，故（3）式在U 内具有唯一的奇点P（0，0）。奇点P（0，0）附近的线性近似方程组为：

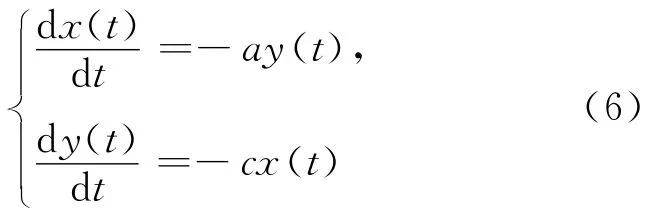
其特征方程为λ2－ac＝0，得，故P（0，0）为鞍点。

定理2 在区域Ω内，初值问题（3）式、（4）式在区间t∈I＝［0，T］上存在唯一的解x（t）与y（t），且（t，x（t），y（t））∈Ω。

证明 分析（3）式及其初始条件，结合初值问题解的局部存在唯一性定理与解的延拓性定理［14］，易得定理2。

定理3 在相平面U 上，（3）式的初始点在S（x0，y0）的相轨线有且只有1条。

证明 （1）由定理2可知，初值问题（3）式、（4）式在区间t∈I＝［0，T］上存在解，设其解为x（t）、y（t），将t看成参数，消去即可得（3）式的初始点在S（x0，y0）的相轨线方程为y＝y（x），并且有（x，y）∈U。

（2）假设（3）式的初始点在 S（x0，y0）有2条不同的相轨线，分别为Γ1、Γ2，则必存在一点M（x＊y＊）∈Γ1、M∈Γ2且Γ1、Γ2在点M 处分叉。由定理2可知初值问题（3）式、（4）式在区间t∈I＝［0，T］上的解是唯一的，Γ1、Γ2不会在点S处分叉，故M≠S。假设Γ1、Γ2过点M的时间分别为t1、t2，所以其对应的积分曲线过（t1，x＊，y＊）、（t2，x＊，y＊）。在点（t，x，y）处再经过充分小的Δt时间内，有，又由于（3）式为自治系统，故Δx、Δy只与该点的x、y值有关而与t无关。从而，Γ1、Γ2不会在点M处分叉，出现矛盾。定理3证毕。

定理4 在相平面U 上，（3）式的初始点在S（x0，y0）的相轨线满足：

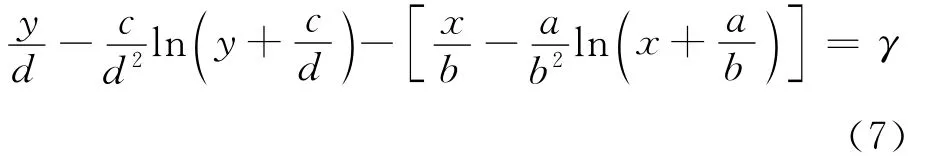
其中

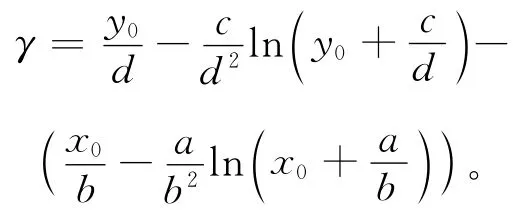
证明 将（3）式的第2个式子除以第1个式子可得：

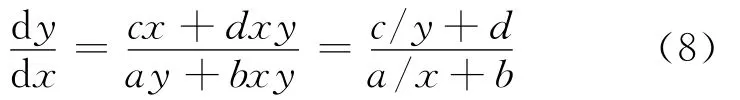
对（8）式分离变量得：

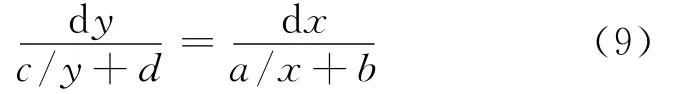
对（9）式两端从0到t积分可得：

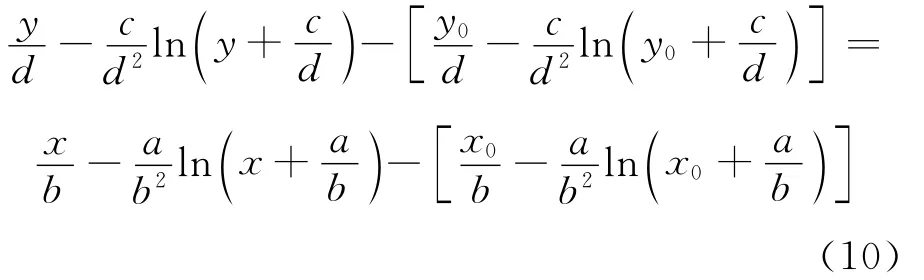
对（10）式进行变形即可得（7）式。定理4证毕。

2 预测战斗结局

定理5（预测战斗结局的判定定理） 假设交战双方兵力变化规律与初始兵力分别满足（3）式、（4）式，则当γ＝ρ时，双方势均力敌；当γ＜ρ时，蓝方将先降为0，即红方将获胜；当γ＞ρ时，红方将先降为0，即蓝方将获胜；且｜γ－ρ｜的值越大，胜方剩余兵力越多。其中，

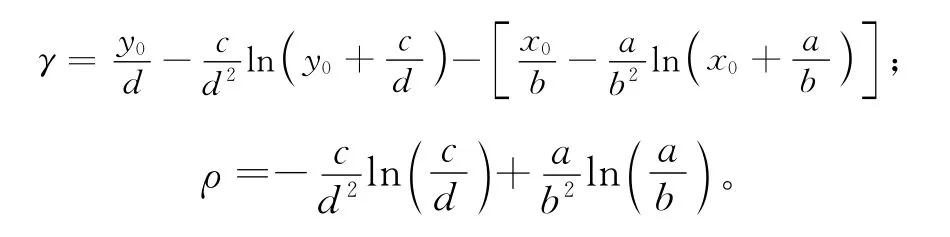
证明 （1）令x＝y＝0，代入（7）式得：

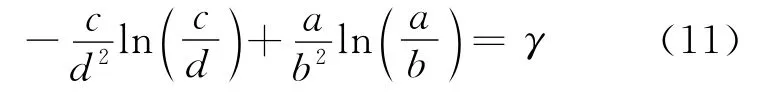
由（11）式可知，当γ＝ρ时，（0，0）满足（7）式，故此时（3）式的相轨线经过（x0，y0）与（0，0）。由定理3可知，（3）式的初始点在S（x0，y0）的相轨线唯一，故红蓝双方此时同时降为0，势均力敌。

（2）令y＝0，代入（7）式得：

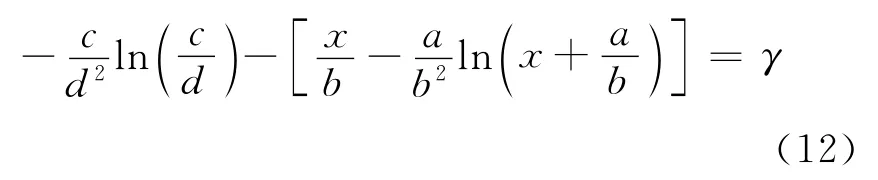
将f、g的具体形式代入（12）式得：

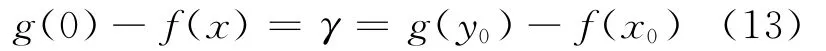
由（13）式可得：

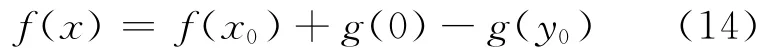
由于g为区间［0，＋∞）上的严格单调递增函数，故g（0）－g（y0）＜0，将其代入（14）式可得：

当γ＜ρ＝g（0）－f（0）时，可得：

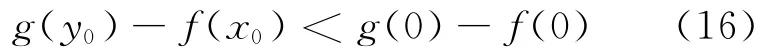
由（14）式、（16）式可得：

从而

由（15）式、（18）式及引理1可知，存在唯一的x1∈（0，x0），使（12）式成立，即代数方程（12）有唯一的解x1∈（0，x0）。从而，当γ＜ρ时，（3）式的相轨线经过（x0，y0）与（x1，0）。由定理3可知（3）式的初始点在S（x0，y0）的相轨线唯一，故此时蓝方兵力先降为0，即红方将获胜，并且红方的剩余兵力为x1，随着ρ－γ的值增大而增大。

（3）同理可得当γ＞ρ时，红方兵力先降为0，即蓝方将获胜。

定理4证毕。

3 算例分析

以模型（1）为例，可得等价数学模型的相应系数为a＝βsub／k，b＝（1－ub）βl／k2，c＝kαsur，d＝（1－ur）αlk2。依据文献［8］，可取x0＝6 000，y0＝10 000，αl＝0.000 01，βl＝0.000 02，αs＝0.1，βs＝0.2，ub＝0.1，当ur分 别 取 0.10、0.14、0.16、0.20时，计算γ与ρ的值、它们之间的大小关系、差的绝对值及战斗结局，见表1所列。

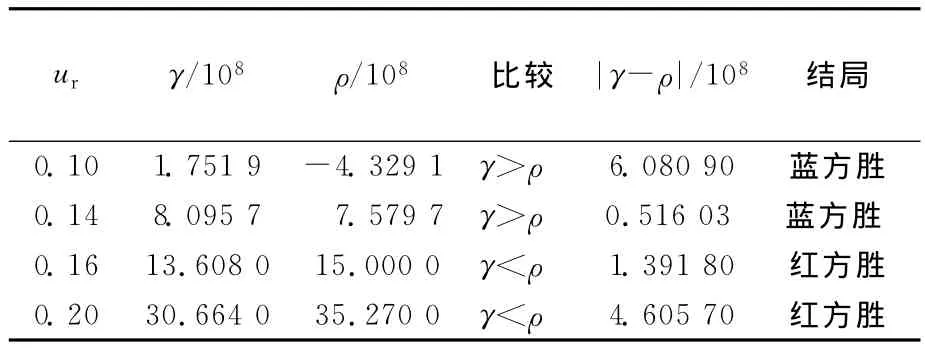
表1 ur取不同值时的胜负分析

为验证所得结果的正确性，当ur分别取0.10、0.14、0.16、0.20时，利用（7）式得到的解析相轨线和利用数值解法得到的对应的数值相轨线进行比较，结果如图1所示。

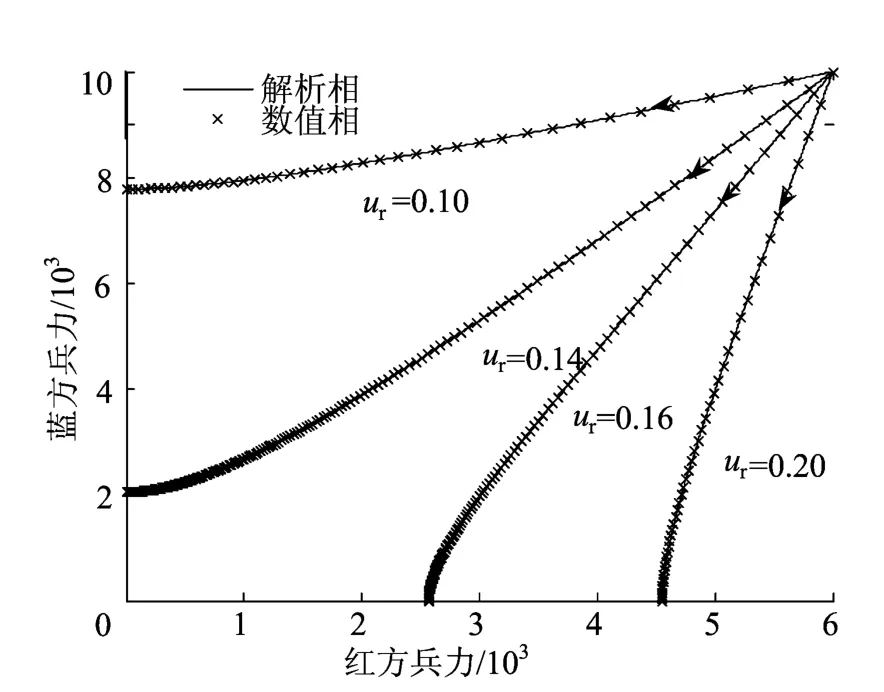
图1 ur取不同值时的解析相轨线与数值相轨线

由图1可知，2种方法得到的相轨线非常地接近，ur取不同值时的战斗结局与表1预测的一致，并且胜方的剩余兵力与｜γ－ρ｜的值成正相关关系，从而证实了相轨线分析的有效性与定理5的正确性。由表1、图1可知，随着ur的增大，战局发生了逆转，尤其是当ur＝0.20时，红方以很小的代价就赢得了战争，这充分体现了加强信息优势的重要性。

4 结束语

本文将基于非线性兰彻斯特方程的信息化战争模型转化为等价形式的数学模型，在一定区域内，讨论了该数学模型的奇点及奇点类型，并得到了模型解的存在唯一性和相轨线的唯一性及其满足的方程。在相轨线方程及其唯一性的基础上，得到了预测战斗结局的判定定理，并进行了算例分析。结果表明，相轨线分析是研究该类兰彻斯特方程的行之有效的方法，也证实了判定定理的正确性。相轨线分析的优点在于可以不具体求解兰彻斯特方程，只需要知道相关系数与初始兵力值就可以预测战斗结局，将结局代入相轨线方程并求解相应的代数方程，即可得到胜方剩余兵力。因此，相轨线分析是能用来分析作战进程和预测战斗结局的简便而有效的方法。还可以通过设置某个系数或初始兵力的系列值，研究战斗结局与胜方剩余兵力的变化规律，可得出各因素对战争胜负的影响程度，从而能为武器装备发展规划、现代军事练兵等提供一定的理论依据。

［1］ Lanchester F W.Aircraft in warfare：the dawn of the fourth arm［M］.London：Lanchester Press，1999：23－45.

［2］ 张最良.军事运筹学［M］.北京：军事科学出版社，1993：167－171.

［3］ Deitchman S J.A Lanchester model of guerrilla warfare［J］.Operations Research，1962，10：818－827.

［4］ Spradlin C，Spradlin G.Lanchester’s equations in three dimensions［J］.Computers and Mathematics with Applications，2007，53：999－1011.

［5］ 冯百胜，周晓光，林亚军.基于随机兰彻斯特理论的舰载机空战效 能 分 析 ［J］.计 算 机 技 术 与 发 展，2013，23（2）：218－221.

［6］ 彭文成，周电杰，张 文.基于协同作战的兵力损耗兰彻斯特方程［J］.运筹与管理，2009，18（3）：128－131.

［7］ 高春蓉，贲可荣.通信对抗仿真中改进的Lanchester作战损耗模型［J］.合肥工业大学学报：自然科学版，2010，33（2）：193－196.

［8］ 吴 俊，杨 峰，梁 彦，等.面向信息化战争的广义兰切斯特作战模型［J］.火力与指挥控制，2010，35（2）：50－53.

［9］ 占栋辉，陈 刚，张宏军，等.现代化战争条件下的兰切斯特战斗模型［J］.计算机工程与应用，2013，49（15）：246－248.

［10］ 莫小平.一类广告微分方程的动力学分析［J］.数学的实践与认识，2009，39（14）：220－223.

［11］ Oliveira R D S，Rezende A C.Global phase portraits of a SIS model［J］.Applied Mathematics and Computation，2013，219：4924－4930.

［12］ 马俊美，纪 青，李水田，等.生态系统的参数确定问题［J］.数学的实践与认识，2008，38（18）：105－113.

［13］ Kantar E，Ertas M，Keskin M.Dynamic phase diagrams of a cylindrical Ising nanowire in the presence of a time dependent magnetic field［J］.Journal of Magnetism and Magnetic Materials，2014，361：61－67.

［14］ 时 宝，张德存，盖明久.微分方程理论及其应用［M］.北京：国防工业出版社，2005：27－40.